Некролог: Митчелл Фейгенбаум, (1944?2019), 4.66920160910299067185320382…

Статья из блога Стивена Вольфрама



Она называется постоянная Фейгенбаума и равняется примерно 4,6692016. И она с завидной периодичностью возникает в определённых видах математических – и физических – систем, способных демонстрировать хаотичное поведение.

Митчелл Фейгенбаум, ушедший от нас 30 июня в возрасте 74 лет, был открывшим её человеком – в 1975 году, и сделал это, занимаясь экспериментальной математикой на карманном калькуляторе.

Это открытие стало определяющим в теории хаоса. Но когда её обнаружили впервые, этот результат был неожиданным, причудливым, не связанным ни с чем из того, что изучалось ранее. Однако некоторым образом тот факт, что её открыл именно Митчелл Фейгенбаум – с которым я был знаком почти 40 лет – кажется подобающим.

Митчелл, обучавшийся теоретической физике, и бывший знатоком её математических традиций, казалось, всегда считал себя аутсайдером. Он был немного похож на Бетховена – и производил элегантное впечатление определённой интеллектуальной тайны. Он часто делал сильные заявления, обычно с заговорщическим видом, с блеском в глазах и бокалом вина или сигаретой в руке.

Он разговаривал длинными витиеватыми предложениями, выдававшими в нём эрудита и интеллектуала. Но идеи из него сыпались самые разные. Иногда они были детальные и технические. Иногда это были скачки интуиции, за которыми, по крайней мере, я уследить не мог. Он всегда что-то читал, не спал до 5-6 часов, заполняя жёлтые страницы записных книжек формулами и загружая систему Mathematica сложными алгебраическими вычислениями, которые могли длиться часами.

Он мало публиковался, а опубликованные работы часто разочаровывали его тем, что их понимало не очень много людей. К моменту смерти он уже много лет работал над оптикой восприятия, и над такими вопросами, как почему Луна кажется больше, находясь над горизонтом. Однако ничего такого он так и не решил опубликовать.

Более 30 лет официальной работой Митчелла (которую он получил, по сути, благодаря открытию постоянной Фейгенбаума) была должность профессора в Рокфеллеровском университете Нью-Йорка (чтобы соответствовать миссии биологических исследований института, его назначили главой «лаборатории математической физики»). Однако он ещё много чем занимался, дал своё имя стартапу финансовых вычислений, и был тесно связан с изобретением новых картографических методов для всемирного атласа Hammond.

Что открыл Митчелл

Основная идея довольно проста. Возьмём число x от 0 до 1. Будем постепенно заменять x на a x (1 – x). Допустим, мы начнём с x = 1/3, и a =3,2. Тогда вот какие последовательные значения x мы будем получать:



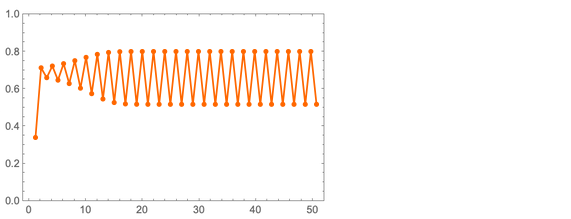
Значения x довольно быстро становятся периодическими, с периодом 2. Но что произойдёт, если взять другие значения a? Вот несколько результатов для т.н. «логистического отображения»:



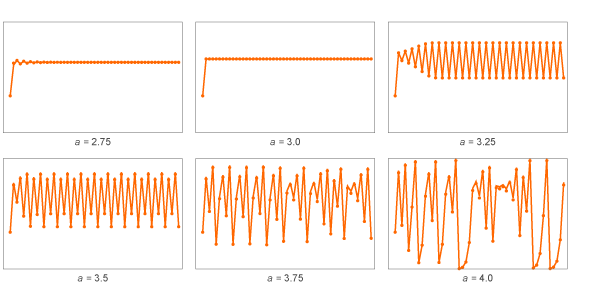
Для малых a значения x быстро приходят к фиксированным. Для крупных a они становятся периодическими, сначала с периодом 2, затем 4. И для более крупных a значения начинают прыгать с кажущимся случайным образом.

Это можно суммировать, построив значения x (здесь их 300, после отбрасывания первых 50) в виде функции от значения a:



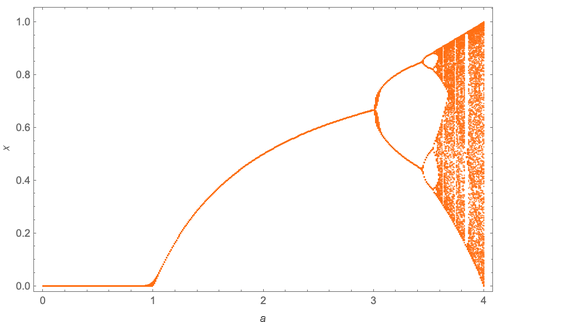
С увеличением a наблюдается каскад удвоения периодов. В данном случае они происходят при a = 3, a ? 3,449, a ? 3,544090, a ? 3,5644072. Митчелл же заметил, что эти последовательные значения имеют предел (a_? ? 3,569946) в геометрической последовательности, a_? – a_n ~ ?^-n и ? ? 4,669.

Интересный результат. Но вот, что придаёт ему значения: это верно не только для определённого итерационного отображения x > a x (1 – x); это верно для любого отображения. Вот, к примеру, «диаграмма бифуркации» для for x > a sin(? vx):



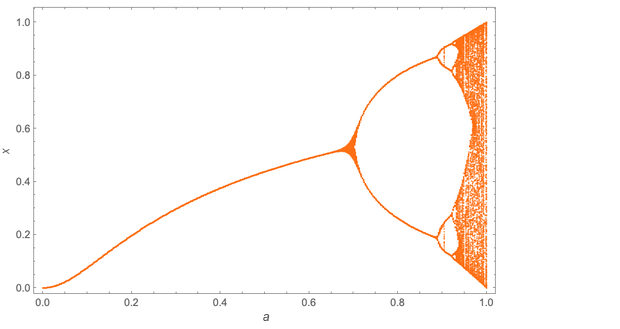
Детали различаются, но Митчелл заметил, что расположение удвоений периодов снова формируют геометрическую последовательность с точно такой же базой ? ? 4.669.

И не только эти различные итерационные отображения давали качественно схожие результаты; при измерении скорости конвергенции она оказывается ровно такой же – всегда ? ? 4.669. Это и стало большим открытием Митчелла: количественно универсальная особенность подхода к хаосу в классе систем.

Научная предыстория

У базовой идеи итеративных отображений длинная история, тянущаяся ещё с античных времён. Ранние их версии возникали в связи с поиском последовательных аппроксимаций, допустим, квадратных корней. К примеру, методом Ньютона из XVII века v2 можно получить итерациями x > 1/x + x/2. Начиная с x=1:



Идея итеративного приближения произвольной функции впервые была формализована, судя по всему, в работе от 1870 года Эрнста Шрёдера (известного формализацией многих вещей, от степеней до булевой алгебры), хотя большая часть обсуждений касалась решения функциональных уравнений, а не самих итераций (за исключением исследования областей сходимости ньютоновской аппроксимации, проделанного Артуром Кейли в 1879). В 1918 Гастон Морис Жюлиа провёл обширное исследование итерационных вещественных функций на комплексной плоскости, изобретя множество Жюлиа. Но до появления фракталов в конце 1970-х (которые вскоре привели к появлению множества Мандельброта) эта область математики прозябала.

Но независимо от исследований чистой математики итеративные отображения с формами, похожими на to x > a x (1 – x), начали появляться в 1930-х среди возможных практических моделей для изучения популяционной биологии или теории бизнес-циклов. Обычно они появлялись в виде дискретных версий непрерывных уравнений, таких, как логистическое уравнение Ферхюльста середины XIX века. Также часто встречалось колебательное поведение – а в 1954 году Уильям Рикер (один из основателей научного рыболовства) также обнаружил более сложное поведение при итерации эмпирических кривых воспроизводства рыбы.

В чистой математике варианты итерационных отображений периодически возникали в теории чисел. В 1799 году Карл Фридрих Гаусс, по сути, изучал отображение x > frac(1/x) в связи с цепными дробями. С конца XIX века появился интерес к отображениям вида x > frac(a x) и их связи со свойствами числа a.

Сразу за работами Анри Пуанкаре по эффективным методам небесной механики в районе 1900-х годов появилась идея чувствительности к начальным условиям, и в итоге было замечено, что итеративные карты могут, по сути, «выкапывать цифры» в начальных условиях. К примеру, итерация x > frac(10 x) по цифрам ? по сути, просто сдвигает последовательность цифр на одну позицию влево с каждым шагом:





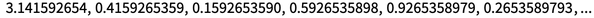
Отображения типа x > a x(1-x) тоже демонстрируют подобное «выкапывание цифр» (к примеру, если заменить x на sin(? u)², то x > 4 x(1-x) превращается точно в u > frac(u, 2), и это было известно ещё в 1940-х – к примеру, это комментировал в 1949 году Джон фон Нейман в связи со своим итеративным методом середины квадратов для генерирования компьютером псевдослучайных чисел.

Однако что по поводу экспериментальной математики на основе итеративных отображений? На ранних цифровых компьютерах экспериментальной математики практически не было (компьютерное время большинства из них было слишком дорогим). Но по следам Манхэттенского проекта в Лос-Аламосе создали свой собственный компьютер MANIAC, который в итоге начали использовать для целой серии исследований в области экспериментальной математики. В 1964 году Пол Стейн и Стэн Улам написали отчёт под заголовком «Изучение нелинейных трансформаций на электронных компьютерах», где приведены фотографии экранов MANIAC, похожих на экраны осциллографов, и на которых демонстрируются итеративные отображения достаточно сложного вида. В 1971 ещё один отчёт, созданный в Лос-Аламосе «из чистого любопытства» (написанный Ником Метрополисом, главой проекта MANIAC и разработчиком метода Монте-Карло, а также Полом Стейном и его братом Мироном Стейном), выдал более конкретные вычислительные результаты для логистических отображений, и отметил базовое явление удвоения периода (авторы назвали его U-последовательность), а также качественную стойкость к изменениям лежащего в основе метода отображения.

Отдельно же от всего этого в физике и математике шли и другие разработки. В 1964 году Эд Лоренц (метеоролог из MIT) ввёл и создал симуляцию своих «естественным образом проявляющихся» дифференциальных уравнений его имени, где была продемонстрирована чувствительность к начальным условиям. С 1940-х годов образовался непрерывный поток математических разработок в области теории динамических систем (работы базировались на достижениях Пуанкаре от 1900-х годов). В частности, они исследовали глобальные свойства решений дифференциальных уравнений. Обычно исследователям встречались фиксированные точки, иногда – предельные циклы. Однако к 1970-м, особенно после появления первых компьютерных симуляций (как у Лоренца) стало ясно, что с нелинейными уравнениями может происходить и нечто иное: т.н. "странный аттрактор". А во время изучения «возвращаемых отображений» странных аттракторов опять начали появляться итерационные отображения.

Однако лишь в 1975 году различные исследования итерационных отображений начали пересекаться. В области чистой математики теоретик динамических систем Джим Йорк и его студент Тьен-Иэнь Ли из Мэрилендского университета опубликовали работу «Хаос вытекает из периода три», где показали, что у итерационного отображения с определённым значением параметра, начальное условие которого приводит к появлению цикла длиной три, должны существовать и другие начальные условия, не приводящие к появлению циклов – или, как они это описали, демонстрирующие хаос. Потом оказалось, что Александр Сарковский, представитель советской школы исследования динамических систем, ещё в 1962 году доказал чуть более слабый результат, в котором из цикла с периодом 3 вытекают циклы со всеми периодами.

В то же время к логистическим отображениям начал расти интерес у математически ориентированных специалистов по популяционной биологии, из которого родился неплохо написанный обзор 1976 года «Простые математические модели с очень сложной динамикой» за авторством австралийского физика по образованию Роберта Мэя, который на тот момент работал профессором биологии в Принстоне (затем он станет научным консультатом британского правительства и получит титул «Барон Мэй Оксфордский»).

Но хотя и существовали такие вещи, как наброски диаграмм бифуркации, открытию их универсальных численных свойств пришлось ожидать появления Митчелла Фейгенбаума.

Путешествие Митчелла

Митчелл Фейгенбаум рос в Бруклине, Нью-Йорк. Отец его был аналитическим химиком, а мать преподавала в государственной школе. Митчеллу не особенно нравилось учиться, хотя он получал хорошие отметки на экзаменах по математике и точным наукам, а также самостоятельно научился матанализу и игре на пианино. В 1960, в 16 лет он, как какой-нибудь вундеркинд поступил в городской колледж Нью-Йорка, официально для изучения электротехники, но также посещал и курсы физики и математики. Закончив учёбу в 1964 году, он поступил в MIT. Сначала он хотел защитить докторскую по электротехнике, но быстро переключился на физику.

И хотя он был в восторге от классической математической физики (как та, что представлена, например, в книгах Ландау и Лифшица), в итоге он писал диссертацию по теме, назначенной его куратором – физика частиц и оценка класса диаграмм Фейнмана для рассеивания фотонов скалярными частицами. Диссертация была не то, чтобы очень интересной, но в 1970 году его отправили в Корнеллский университет на позицию постдока.

У Митчелла начались проблемы с мотивацией, и вместо занятий физикой он предпочитал проводить время в кафешках, разгадывая кроссворды в New York Times (что ему удавалось делать с большой скоростью). Но в Корнелле Митчелл завёл нескольких важных для себя друзей. Одним из них был Предраг Цвитанович, выдающийся аспирант из той части Югославии, что теперь называется Хорватия; он изучал квантовую электродинамику, и разделял с Митчеллом интерес к немецкой литературе. Другим была молодая поэтесса Кэтлин Дуриш (позднее ставшая Кэти Хэммонд), подруга Предрага. Ещё одним был восходящая звезда физики, профессор Пит Каррутерс, разделявший с Митчеллом интерес к классической музыке.

В начале 1970-х наступал золотой век квантовой теории поля. Но, несмотря на тему своей работы, Митчелл не занимался этим, и после двух лет в Корнелле не выдал никаких результатов. Однако ему удалось произвести впечатление на Ханса Бете, и тот перевёл его на другое место, также в качестве постдока, но в институт, занимающий в неофициальной иерархии место чуть пониже – Виргинский политехнический.

В Виргинском институте Митчелл делал ещё меньше, чем в Корнелле. Он практически не общался с людьми, и выдал всего одну работу на три странички: «Взаимосвязь коэффициента нормализации и функции дисперсии в уравнении транспорта мультигрупп». Как ясно из названия, работа была технической и неинтересной.

По окончанию двухлетнего пребывания Митчелла в Виргинии не было понятно, что последует дальше. Однако вмешалась удача. Друга Митчелла из Корнелла, Пита Каррутерса, наняли с целью создания теоретического подразделения в Лос-Аламосе, и дали карт-бланш на найм нескольких выдающихся молодых физиков. Пит потом рассказывал мне с гордостью (в рамках советов по научному менеджменту), что у него было такое чувство, что Митчелл способен на нечто великое, и, несмотря на мнение других людей – и свидетельства – он решил поставить на него.

Переведя Митчелла в Лос-Аламос, Пит начал предлагать ему проекты. Сначала это было продолжение работ Пита, попытки подсчитать груду коллективных («транспортных») свойств квантовой теории поля, чтобы понять высокоэнергетические столкновения частиц – это были работы, предшествующие исследованиям кварк-глюонной плазмы.

Но вскоре Пит предложил Митчеллу заняться турбулентностью в жидкостях, в частности, выяснить, не помогут ли в этом деле методы ренормализационной группы.

Когда жидкость – например, вода – начинает течь достаточно быстро, в ней появляются маленькие водовороты, и она начинает вести себя сложным, и, на первый взгляд, случайным образом. Но хотя качественно это явление обсуждалось уже много веков (к примеру, его зарисовки делал даже Леонардо да Винчи), физики могли рассказать о нём примечательно мало – хотя в 1940-х Андрей Николаевич Колмогоров сделал замечание о том, что водовороты должны формировать каскад с k-распределением энергий. В Лос-Аламосе учёные концентрировались на разработке атомного оружия (что неизбежно включает в себя изучение поведения жидкостей с сильным течением), и турбулентность очень важно было понять – хотя и не было очевидно, как к ней подступиться.

В 1974 появилась новость о том, что Кеннет Вильсон из Корнелла «решил проблему Кондо» [проблема Кондо – неспособность теоретической физики объяснить эффект Кондо / прим. перев.] при помощи техники под названием «ренормализационная группа». Пит Каррутерс предложил Митчеллу применить эту технику к турбулентности.

Ренормализационная группа связана с тем, как изменение масштаба (или других параметров) влияет на описание (и поведение) систем. Случилось так, что руководитель Митчелла по докторской из MIT, Фрэнсис Лоу, совместно с Мюрреем Гел-Манном вновь ввёл её в 1954 году в контексте квантовой электродинамики. Идея лежала без движения много лет, но в 1970-х вернулась, и активно – хотя по-разному – применялась как к физике частиц (особенно в квантовой хромодинамике), так и к физике конденсированных состояний.

В кусочке железа, находящемся в комнате, можно выровнять спины всех электронов, связанных с каждым атомом, и тогда железо намагнитится. Но если разогреть железо, в нём начнутся флуктуации, и внезапно – при температуре выше т.н. точки Кюри (770°C для железа) – в железе появляется столько случайности, что его магнитные свойства исчезают. Вообще, существует довольно много ситуаций (плавление, кипение, формирование транспортных заторов), когда происходит этот внезапный т.н. фазовый переход.

Но что конкретно происходит во время фазового перехода? Думаю, проще всего увидеть это, изучая его аналог в области клеточных автоматов. С определённым правилом, приведённым ниже, когда у системы изначально нет большого количества чёрных клеток, вскоре она вся станет белой. Но если увеличить количество первоначальных чёрных клеток (по аналогии с увеличением температуры магнитной системы), тогда внезапно, в данном случае при 50% доле чёрных клеток, происходит резкий переход, и вся система в итоге становится чёрной (замечание для экспертов по фазовым переходам: да, это фазовый переход в одномерной системе; двумерная может понадобиться только, если системе необходимо быть микроскопически обратимой).



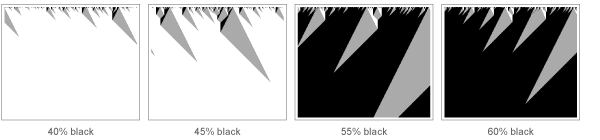
Но что происходит с системой близ границы в 50% чёрных клеток? По сути, она не может решить, стать ли ей чёрной или белой. В итоге она показывает целую иерархию флуктуаций, от самых мелких до самых крупных масштабов. К 1960-м стало понятно, что «критические экспоненты», характеризующие степенные законы, описывающие эти флуктуации, одинаковы для множества систем.

Но как нам подсчитать эти критические экспоненты? В некоторых искусственных случаях были известны аналитические методы. Но по большей части требовалось нечто другое. В конце 1960-х Кен Вильсон понял, что можно использовать ренормализационные группы и компьютеры. Можно построить модель взаимодействия отдельных спинов. Но ренормализационная группа даёт вам процедуру «масштабирования» для взаимодействий всё более и более крупных блоков спинов. И изучая это на компьютере, Кен Вильсон сумел начать вычислять критические экспоненты.

Сначала физики не обращали на это должного внимания, не в последнюю очередь потому, что не привыкли к такому активному использованию компьютеров в теоретической физике. Но затем появилась проблема Кондо. В большинстве материалов электрическое сопротивление уменьшается с уменьшением температуры (а в сверхпроводниках уменьшается до нуля даже при температурах больше абсолютного нуля). Однако в 1930-х измерения на золоте показали, что его сопротивление увеличивается при низких температурах. К 1960-м считалось, что всё дело в рассеивании электронов на магнитных примесях – однако подсчёты столкнулись с неприятностями, выдавая бесконечности в результатах.

Затем в 1975 году Кен Вильсон применил свои методы ренормализационной группы – и смог точно вычислить эффект. Этот эффект до сих пор окутан некоей тайной (тому, вероятно, способствует тот факт, что мне часто с трудом удавалось понимать объяснения Кена Вильсона по этой теме, по крайней мере с тех пор, как я познакомился с ним в 1980-х). Но идея того, что ренормализационная группа может быть важной, прижилась.

Как её можно применить к турбулентности жидкостей? Степенной закон Колмогорова давал определённые идеи. Но можно ли было взять уравнения Навье-Стокса, управляющие потоком идеализированной жидкости, и вывести что-нибудь из них? Этим проектом и занялся Митчелл Фейгенбаум.

Крупное открытие

С уравнениями Навье-Стокса очень тяжело работать. По сей день не очень понятно, как даже наиболее очевидное свойство турбулентности – его кажущаяся случайность – вытекает из них. Возможно, эти уравнения не являются полным или непротиворечивым математическим описанием, и мы на самом деле видим усиленные микроскопические движения молекул. Возможно – как в теории хаоса и уравнениях Лоренца – всё дело в усилении случайности в исходных условиях. Лично я на основе моей работы от 1980-х считаю, что всё дело в свойствах их внутренних вычислений, аналогичных случайности в моём "правиле 30" для клеточного автомата.

Как же подошёл к этой проблеме Митчелл? Он попытался её упростить – сначала перейдя от уравнений, зависящих от пространства и времени, к уравнениям, зависящим только от времени, а потом сделав их дискретными и изучая итерационные отображения. От Поля Штейна Митчелл знал о предыдущей работе над итерационными отображениями, проделанной в Лос-Аламосе (которая не была широко известной). Но Митчелл не понимал, в какую сторону двигаться дальше, хотя, получив в своё распоряжение новенький сверхсовременный программируемый калькулятор HP-65, он решил запрограммировать на нём итерационные отображения

Потом, в июле 1975 года, Митчелл отправился на летнюю физическую встречу в Аспен, Колорадо. Там он встретился со Стивеном Смэйлом, известным математиком, изучавшим динамические системы, и удивился, узнав, что тот рассказывает об итерационных отображениях. Смэйл упомянул, что кто-то спрашивал его, можно ли выразить предел каскада с удваивающимся периодом a_? ? 3,56995 через стандартные константы типа ? и v2. Смэйл не знал ответа на этот вопрос. Однако Митчелл заинтересовался этим, и решил попробовать узнать ответ.

У него не было с собой HP-65, однако он погрузился в этот вопрос, используя стандартные инструменты образованного математического физика, и вскоре превратил задачу в поиск полюсов функций на комплексной плоскости, о которой ему особенно нечего было сказать. Однако вернувшись в Лос-Аламос в августе, он обратился к своему HP-65, и начал программировать его с целью обнаружения точек бифуркации a_n.

Для небольших n итерация шла довольно быстро. Для n = 5 на неё уходило 30 секунд. Для n = 6 приходилось ждать уже несколько минут. Однако, пока калькулятор работал, Митчелл решил посмотреть на значения a_n, которые у него уже были, и кое-что заметил: казалось, что они геометрически стремятся к некоему финальному значению.

Сначала он просто использовал этот факт для оценки a_?, которую ему, несмотря на все попытки, не удалось выразить через стандартные константы. Но вскоре он начал подозревать, что экспонента конвергенции ? была важнее, чем a_? — поскольку её значение оставалось неизменным при простых изменениях переменных в отображении. Около месяца Митчелл пытался выразить ? в терминах стандартных констант.

Но затем, в октябре 1975 года, он вспомнил, что Пол Штейн говорил, что удвоение периода выглядит одинаково не только для логистических отображений, но вообще для всех итерационных отображений с одним максимумом. Воссоединившись со своим HP-65 после поездки в Калтех, Митчелл сразу же попробовал отображение x > sin(x) и обнаружил, что с точностью до трёх цифр после запятой экспонента ? была точно такой же.

Он сразу решил, что наткнулся на нечто замечательное. Но Штейн сказал, что ему потребуется больше цифр, чтобы делать выводы. В Лос-Аламосе было много мощных компьютеров, поэтому на следующий день Митчелл попросил кого-то показать ему, как писать программу на FORTRAN, чтобы продвинуться дальше – и к концу дня он сумел вычислить, что в обоих случаях ? имела значение около 4,6692.

Использованный им компьютер был типичной рабочей лошадкой для науки США в те дни: модель CDC 6000 (того же типа, что использовал я, когда впервые переехал в США в 1978). Её разработал Сеймур Крэй, и по умолчанию она использовала 60-битные числа с плавающей запятой. Но с такой точностью (14 цифр после запятой) Митчелл не мог получить ничего лучше, чем 4,6692. К счастью, жена Пита, Люси Каррутерс, была программистом в Лос-Аламосе, и она показала Митчеллу, как использовать удвоенную точность. В итоге он смог вычислить ? с точностью до 11 чисел после запятой, и определить, что значения двух разных итерационных отображений получаются одинаковыми.

В течение нескольких недель Митчелл обнаружил, что ?, судя по всему, является универсальным значением для всех итерационных карт с одним квадратичным максимумом. Но он не знал, почему так происходит, и у него не было какого-то определённого математического аппарата для исследования этого вопроса. Но в итоге, в возрасте 30 лет, Митчелл обнаружил что-то, что показалось ему по-настоящему интересным.

На свой день рождения 19 декабря Митчелл встретился со своим другом Предрагом и рассказал ему об этом результате. Однако в то время Предраг работал с мэйнстримовой физикой частиц, и не придал этому особого значения.

Митчелл продолжал работать, и через несколько месяцев убедился, что универсальной была не только экспонента ? — при должном масштабе были универсальными и сами итерационные отображения. В апреле 1976 года Митчелл написал отчёт о своих результатах. 2 мая 1976 он рассказал о них в докладе в институте передовых исследований в Принстоне. Там присутствовал Предраг, и тогда он, наконец, заинтересовался работой Митчелла.

Но Предрагу довольно часто было непонятно, о чём говорит Митчелл. Но на следующий день Предраг успешно сумел упростить задачу и получить одно непосредственное функциональное уравнение для ограниченной формы масштабированной итерационной карты: g(g(x)) = -g(? x)/?, где ? ? 2,50290, из чего следовало, что для любого итерационного отображения определённого типа его ограниченная форма будет выглядеть, как более извилистая версия этого отображения:

Как всё развивалось

Область исследования итерационных отображений получила импульс 10 июня 1976 года после публикации в журнале Nature обзора от Роберта Мэя, который он написал независимо от Митчелла, и, естественно, без упоминания полученных им результатов. Но в последовавшие месяцы Митчелл ездил со своими докладами о полученных им результатах. Реакция на них была смешанной. Физикам было интересно, как эти результаты соотносятся с физикой. Математикам был непонятен их статус, учитывая, что они были получены из экспериментальной математики и не имели формального математического доказательства. И, как обычно, людям было трудно понимать объяснения Митчелла.

Осенью 1976 Предраг устроился в Оксфорд на должность постдока, и в самый первый день, когда я появился там, 17-летний студент, пишущий диплом по физике частиц, я встретился именно с ним. Мы в основном беседовали о его элегантном методе «птичьих следов» для работы с теорией групп (книгу о котором он, наконец, опубликовал 32 года спустя). Также он пытался объяснить мне итерационные отображения. И я всё ещё помню, как он рассказывал об идеализированной модели популяции рыбы в Адриатическом море (лишь спустя годы я связал это с тем, что Предраг был из тех мест, которые сейчас называют Хорватией).

В то время я не придал этому значения, но идея итерационных отображений закрепилась в моём сознании, и вскоре смешалась с идеей фракталов, о которых я узнал из книги Бенуа Мандельброта. И когда через пару лет я сконцентрировался на проблемах сложности, эти идеи помогли мне прийти к таким системам, как клеточные автоматы.

Но в 1976 году Митчелл (до следующей моей встречи с которым пройдёт ещё несколько лет) активно ездил с докладами о полученных результатах. Он также отправил работу в престижный научный журнал Advances in Mathematics. Шесть месяцев он не получал оттуда вестей, но в итоге работу отвергли. Он попробовал снова, отправив другую работу в SIAM Journal of Applied Mathematics – с тем же результатом.

Хочу сказать, что не удивлён этим. По моему опыту публикаций в академической литературе (чем я не занимался уже очень давно), опубликовать работу в определившейся области исследований довольно легко. Но работа в области чего-то по-настоящему нового или оригинального может практически положиться на то, что её отвергнут после экспертной оценки – либо из-за интеллектуальной близорукости, либо из-за академической коррупции. У Митчелла была ещё одна проблема – его объяснения было сложно понять.

Но, наконец, в 1977 году Джоэл Лебовиц, редактор Journal of Statistical Physics, согласился опубликовать работу Митчелла – по сути, по причине знакомства с ним, ведь он признал, что работу не понял. Так и появилась работа 1978 года «Количественная универсальность в классе нелинейных трансформаций», описывающая большое достижение Митчелла. В целях расстановки академических приоритетов Митчелл иногда цитировал краткое изложение доклада, сделанного им 26 августа 1976 года, и опубликованного в ежегодном сборнике отчётов Los Alamos Theoretical Division за 1975-1976 года. На Митчелла сильно повлияли отказы в публикации его работ, и он годами хранил письма с отказами в ящике стола.

Митчелл продолжал ездить по миру с докладами о полученных результатах. Интерес к ним был, но было и недоумение. Однако летом 1979 года случилось нечто потрясающее: Альберт Либхабер из Парижа сообщил о результатах физического эксперимента по переходу к турбулентности в конвекционных потоках жидкого гелия, где он увидел удвоение периода точно с той экспонентой ?, которую вычислил Митчелл. Она оказалась универсальной не только для класса математических систем, но и проявила себя в реальных, физических системах.

И мгновенно Митчелл стал знаменит. Была обнаружена связь с ренормализационной группой, его работа стала модной как у физиков, так и у математиков. Митчелл продолжал ездить с докладами, но теперь он имел возможность регулярно тусить с лучшими физиками и математиками.

Помню, как он приехал в Калтех, где-то осенью 1979 года. Всё это напоминало встречу с рок-звездой. Митчелл приехал, сделал стильный, но немного загадочный доклад, а потом его умыкнули для приватной беседы Ричард Фейнман и Марри Гелл-Ман.

Вскоре Митчеллу предложили кучу различных высококлассных рабочих мест, и в 1982 году он с триумфом вернулся в Калтех как профессор по физике. Были разговоры о том, что открытие достойно нобелевки, и к июню 1984 года он появился в журнале New York Times, с бетховеновским шиком, на фоне водопада в Корнелле:



Но математики оставались недовольными. Как и в случае работы Бенуа Мандельброта, они считали результаты Митчелла «численными гипотезами», недоказанными, и недостойными упоминания. Однако лучшие математики (с которыми подружился Митчелл) вскоре начали работать над этой задачей, и результаты не заставили себя ждать – хотя до полного и окончательного доказательства универсальности ? прошло целых десять лет.

Куда делась наука

Что же случилось с крупным открытием Митчелла? Оно, конечно, стало знаменитым. И каскады с удвоением периода с его универсальными свойствами вскоре нашлись в целом ряде систем – в жидкостях, оптике и т.д. Но насколько они были общими? Можно ли было расширить их на всю проблему турбулентности в жидкости?

Митчелл и другие изучали системы, отличные от итерационных отображений, и находили связанные явления. Но среди них не было таких удивительных, как первое открытие Митчелла.

В каком-то смысле, мои попытки изучения клеточных автоматов и поведения простых программ, начатые в 1981 году, были нацелены на поиски некоторых из тех больших вопросов, к которым могла привести и работа Митчелла. Однако наши методы и результаты получились весьма разными. Митчелл всегда пытался оставаться поближе к таким вещам, к которым могут обращаться традиционные математические физики, а я бесстрашно отправился в вычислительную вселенную, исследуя встречающиеся там явления.

Я пытался понять, как работа Митчелла может быть связана с моей, и в своей первой работе по клеточным автоматам в 1981 году даже отметил, к примеру, что среднюю плотность чёрных клеток в последовательных шагах эволюции клеточного автомата можно приблизительно оценить через итерационное отображение.

Я также отметил, что математически всю эволюцию клеточного автомата можно рассматривать, как итерационное отображение – хотя и не на множестве обычных вещественных чисел, а на канторовом множестве. В моей первой работе я даже построил аналог гладких отображений Митчелла, однако у меня они были дикими и прерывистыми:



Но, как бы я ни пытался, я так и не смог найти явных связей с работой Митчелла. Я искал аналоги удвоения периода или порядка Шарковского, но ничего особенного не нашёл. Для моей вычислительной платформы даже задумываться о вещественных числах с их бесконечными последовательностями цифр было неестественно. Много лет спустя, в книге «Новый вид науки», я вставил заметочку «Плавные итерационные отображения». Я показал их последовательность цифр и наблюдал, как открытие Митчелла подразумевает наличие необычной вложенной структуры в начале последовательностей:

Конец истории

Что же стало с Митчеллом? Проведя четыре года в Корнелле, он перебрался в Рокфеллеровский университет в Нью-Йорк, и следующие 30 лет вёл практически богемное существования, проводя большую часть времени у себя в апартаментах в Верхнем Истсайде на Манхэттене.

Будучи в Лос-Аламосе, Митчелл женился на женщине немецкого происхождения по имени Корнелия, сестре физика (и моего давнего друга) Дэвида Кэмпбелла, основавшего центр нелинейных исследований в Лос-Аламосе, а затем ставшего ректором Бостонского университета. Однако довольно быстро Корнелия ушла от Митчелла, причём не к кому иному, как к Питу Каррутерсу. Позднее Пит, страдавший от алкоголизма и других проблем, воссоединился со своей женой Люси, однако в 1997 умер в возрасте 61 года.

В Корнелле Митчелл познакомился с Гуниллой, которая в возрасте 14 лет сбежала из семьи пастора из небольшого городка в северной Швеции, и сначала была натурщицей у Сальвадора Дали, а потом в 1966 году приехала в Нью-Йорк в качестве манекенщицы. Гунилла была журналистом, вела видеосъёмку, писала пьесы и рисовала картины. Они поженились с Митчеллом в 1986 году, и их брак продлился 26 лет, в течение которых Гунилла сделала неплохую карьеру в фигуративном искусстве.

Последняя работа, написанная Митчеллом самостоятельно, была опубликована в 1987 году. Он также публиковал множество работ с различными соавторами, хотя ни одна из них не стала особенно примечательной. Большинство из них продолжали его ранние исследования, или пытались применять традиционные методы математической физики к различным сложным явлениям, сходным с течением жидкости.

Митчеллу нравилось взаимодействовать с верхними эшелонами академических кругов. Он получил всяческие награды и знаки признания (кроме Нобелевской премии). Но он до конца считал себя аутсайдером – человеком эпохи Возрождения, сфокусировавшимся на физике, но не уверовавшим до конца во все институты и практики.

С начала 1980-х я довольно регулярно виделся с Митчеллом, в Нью-Йорке и других местах. Он ежедневно использовал платформу Mathematica, хвалил её и часто рассказывал о сложных вычислениях, которые он с её помощью проводил. Как многие математические физики, Митчелл был знатоком специальных функций, и часто беседовал со мной о всё более и более экзотических функциях, которые, по его мнению, нам следовало бы добавить в продукт.

У Митчелла было два крупных увлечения за пределами академической области. В середине 1980-х молодая поэтесса, которую сейчас зовут Кэти Хэммонд, и которую Митчелл знал с Корнелла, была менеджером по рекламе в газете New York Times, и вышла замуж за человека из семьи, владевшей издательством всемирного атласа Хэммонда. Через неё Митчелл погрузился в совершенно новый для себя мир картографии.

Я много раз беседовал с ним на эту тему. Он гордился тем, что придумал, как использовать теорему Римана об отображении для получения специальных локальных отображений при создании карт. Он описывал мне основанный на физике алгоритм размещения меток на картах (хотя я его до конца так и не понял). Его очень порадовал выход нового издания атласа Хэммонда (которое он потом называл «мой атлас»).

С 1980-х годов активно развивалась тенденция применения физических идей к количественным финансам, и физики часто становились аналитиками для Уолл-Стрит. А поскольку финансисты постоянно ищут уникальные преимущества, к новым методам всегда существует интерес. Со мной очень часто связывались с подобными вопросами – но после успеха книги Джеймса Глейка 1987 года «Хаос» (по поводу которой я давал длинное интервью) появилась целая толпа людей, желающих узнать, как «хаос» может помочь им в управлении финансами.

Одним из них был некто Майкл Гудкин. Обучаясь в колледже в начале 1960-х, Он основал компанию по юридическим исследованиям для студентов, изучавших юриспруденцию. Через несколько лет он нанял нескольких экономистов, обладателей Нобелевской премии, и основал, возможно, первый хедж-фонд, занимавшийся арбитражными торгами при помощи компьютеров. Гудкин всю жизнь был мотом, любил азартные игры, путешествия и нарды, и заработал много денег. В один из неудачных моментов он искал какое-либо новое решение – и обнаружил теорию хаоса и Митчелла Фейгенбаума.

Несколько лет он обрабатывал разных физиков, а потом в 1995 году набрал команду и основал компанию Numerix для коммерциализации использования физических методов вычислений в области всё более экзотических финансовых инструментов. Митчелл Фейгенбаум был лицом компании, хотя всю тяжёлую работу тащил мой давний друг Найджел Голденфилд и его молодой коллега Саша Сокол.

С самого начала в компании было много работы, связанной с математической физикой, и Митчелл активно участвовал в ней. Он был большим любителем стохастического исчисления Ито, читал по нему лекции и гордился тем, что нашёл метод тысячекратного ускорения стохастического интегрирования. Однако на самом деле компания писала библиотеки на C++ для интеграции в системы банков. Митчелл не хотел заниматься чем-то подобным в долгосрочной перспективе. После нескольких лет работы его активность в компании снизилась.

Я встречался с Гудкиным в 1998 году, а потом 14 лет спустя. Незадолго до этого он написал автобиографию «Неправильный ответ получить быстрее: конфиденциальная история создания машины, торгующей триллионами», и внезапно связался со мной, предлагая участвовать в новом непонятном деле. Митчелл всё ещё хорошо отзывался о Майкле, хотя когда разговор внезапно зашёл о том, чтобы я основал новую компанию и стал её директором, я отказался.

Все эти годы я довольно часто общался с Митчеллом, хотя наши контакты не так хорошо сохранились в архиве, как могли бы быть, поскольку он больше любил общаться голосом, чем по почте. Он написал мне однажды: «Мне не нравится переписываться по емейлу. Я до сих пор предпочитаю слышать голос и взаимодействовать с человеком».

Но в моём архиве сохранились какие-то фрагменты. Есть, к примеру, переписка касательно 60-го дня рождения Митчелла в 2004 году, на которое я не попал, поскольку он пересекался с днём рождения одного из моих детей. Вместо этого я заказал изготовление «Кристалла Фейгенбаума-Цвитановича» – трёхмерной стеклянной скульптуры, изображающей ограничение функции g(z) на комплексной плоскости.

Решить функциональное уравнение было немного сложно, и лазерная гравировка сначала расколола парочку стеклянных блоков, но в итоге этот объект удалось изготовить и отправить – и много лет спустя мне было приятно увидеть его на полке в квартире Митчелла:



Иногда у меня в архивах всплывают упоминания Митчелла другими людьми, обычно Предрагом. В 2007 году Предраг писал мне (со своим характерным чувством юмора):

К другим новостям: только что встретил Митчелла, он встречается с Одиссеей.

Я имею в виду не дорогую эскортную службу, а «Одиссею» Гомера. Он занялся вычислением местоположения звёзд как функции с 26000 летней прецессией. Он говорит, что Гиппарх всё это когда-то рассчитал, но католической церкви удалось уничтожить все копии его табличек".

Оправдывая свой образ человека эпохи Возрождения, Митчелл всегда серьёзно интересовался историей. В 2013 году в ответ на мою статью о Лейбнице, Митчелл сказал, что он был любителем Лейбница с подростковых времён, и пояснил:

"Агиограф Ньютона, Вольтер, понятия не имел о сущности монадологии, поэтому мог подделать только «лучший из всех возможных миров». Давным-давно я опубликовал это как устное средство объяснения универсальности 2 ⁿ.

Вторая из работ Лейбница, опубликованная, когда ему было 19, «О методах обращения тангенсов», или что-то типа того, содержала изобретение метода изоклиналей для решения обыкновенных дифференциальных уравнений. Лейбниц и Ньютон начинают с дифференциальных уравнений, уже получив дифференциальное счисление. Очень интересная история".

Однако оплотом интеллектуальной жизни Митчелла всегда была математическая физика, хотя больше в личном плане, чем как часть академической работы. В какой-то момент его крестница, будучи совсем юной, спросила его, почему Луна, располагаясь ближе к горизонту, кажется большей по размеру. Он написал ей ответ (немного напоминающий письма Эйлера к немецкой принцессе), а потом понял, что не уверен в ответе, и пустился в многолетние исследования оптики и формирования изображений. Попав в MIT, он заинтересовался работой сетчатки, вдохновившись книгой Джерри Леттвина «Что глаз лягушки говорит мозгу лягушки».

Он рассказывал мне об этом, говоря, что обычная теория формирования изображений неверна, и что у него есть теория получше. Он всегда использовал в качестве примера размер Луны, но я не был уверен, была ли эта проблема связана с оптикой или с восприятием. Он так и не опубликовал связанных с этой темой работ, хотя при некотором везении его рукописи (по слухам, он готовил книгу), в итоге увидят свет – если их кто-нибудь ещё сможет понять.

Когда я бывал в гостях у Митчелла с Гуниллой, их апартаменты производили богемное впечатление – повсюду были книги, бумаги, картины, и разные подобные штуки. А ещё там была Птица. Это был какаду, и он был громкий. Не знаю, кто и зачем его принёс. Но он доставлял изрядно хлопот. Митчелла и Гуниллу чуть не выгнали из апартаментов из-за жалоб соседей на шум, и в итоге они возили Птицу по врачам. Как я узнал потом, неожиданно ознакомившись с так и не осуществлённым планом по разработке видеоигр для домашних животных («чужого разума на нашей планете»), какаду – существа социальные, и таким питомцам определённо нужен «твиттер для какаду».



В итоге из семьи ушла Гунилла, и, по слухам, именно из-за Птицы.

В последний раз мы встречались с Митчеллом лично несколько лет назад. Мы с моим сыном Кристофером приезжали к нему в гости – и он был по-митчелловски возбуждён, глаза его сверкали, говорил он быстро и немного загадочно на тему математической физики формирования изображений. «Глаза птиц переоценены, — говорил он под шум своего какаду из соседней комнаты. Центральная ямка у них очень маленькая. Их глаза работают как телескопы».

«Лучше всего глаза у рыб, — сказал он, объясняя, что все глаза появились в результате эволюции под водой – и с тех пор их архитектура особо не менялась. – Рыбы удерживают в фокусе всё поле зрения целиком, в отличие от нас», — сказал он. Это было очаровательно, эксцентрично и очень по-митчелловски.

Годами мы периодически беседовали по телефону, обычно поздно вечером. Несколько месяцев назад я встретил Предрага, и сказал ему, что удивлён тем, как давно не говорил с Митчеллом. Он пояснил, что Митчелл болеет, но никому об этом не рассказывает. А несколько недель назад в районе полуночи Предраг отправил мне емейл с темой «Митчелл мёртв», с пояснением, что Митчелл умер в районе 20 часов, и приложил к письму характерную фотографию «Митчелл в Нью-Йорке»:



С годами я выработал у себя определённый ритуал – когда я слышу о смерти знакомого, я сразу начинаю искать его у себя в архивах. И я неожиданно обнаружил, что несколько лет назад Митчелл дозвонился до моей голосовой почты, о существовании которой я и не подозревал. Поэтому теперь я могу дать Митчеллу возможность сказать последнее слово.

И, естественно, написать последнее число: 4.66920160910299067185320382…