
Тема Аллокаторов частенько всплывает на просторах интернета: действительно, аллокатор — эдакий краеугольный камень, сердце любого приложения. В этой серии постов я хочу в подробностях рассказать о одном весьма занимательном и именитом аллокаторе — JeMalloc, поддерживаемый и развиваемый Facebook и используемый, например, в bionic[Android] lib C.
В сети мне не удалось найти каких-либо подробностей, полностью раскрывающих душу данного аллокатора, что по итогу сказалось на невозможности сделать какие-либо выводы о применимости JeMalloc при решении той или иной задачи. Материала вышло очень много и, дабы читать его было не утомительно, начать предлагаю с основ: Базовых Структур Данных используемых в JeMalloc.
Под катом рассказываю о Pairing Heap и Bitmap Tree, формирующих фундамент JeMalloc. На данном этапе я не затрагиваю тему многопоточности и Fine Grained Locking, однако, продолжая серию постов, обязательно расскажу про эти вещи, ради которых, собственно, и создается разного рода Экзотика, в частности и та, что описывается ниже.
Bitmap_s — древовидная структура данных, которая позволяет:
- Быстро находить первый установленный / неустановленный бит в заданной последовательности битов.
- Менять и получать значение бита с индексом i в заданной последовательности битов.
- Дерево строится по последовательности из n бит и обладает следующими свойствами:
- Базовой единицей дерева является узел, а базовой единицей узла — бит. Каждый узел состоит из ровно k бит. Битность узла выбирается таким образом, чтобы вычисления логических операций над выбранным диапазоном бит производились максимально быстро и эффективно на данной ЭВМ. В JeMalloc узел представлен unsigned long типом.
- Высота дерева измеряется уровнями и для последовательности из n бит составляет H = уровней.
- Каждый уровень дерева представлен последовательностью из узлов, что эквивалентно последовательности из бит.
- Самый верхний(корневой) уровень дерева состоит из k бит, а самый нижний — из n бит.
- Каждый бит узла уровня L, определяет состояние всех битов дочернего узла уровня L — 1: если бит установлен в состояние 'занят', то все биты дочернего узла также установлены в состояние 'занят', в противном же случае, биты дочернего узла могут иметь как 'занятое' так и 'свободное' состояние.
Разумно представлять bitmap_t двумя массивами: первый, размерности равной количеству всех узлов дерева — для хранения узлов дерева, второй, размерности высоты дерева — для хранения смещения начала каждого уровня в массиве узлов дерева. При таком способе задания дерева сначала может идти корневой элемент, а затем, последовательно, узлы каждого из уровней. Однако, авторы JeMalloc хранят корневой элемент последним в массиве, а перед ним располагают узлы нижележащих уровней дерева.
В качестве наглядного примера возьмем последовательность из 92-ух бит и K = 32-ум. Будем полагать, что состояние 'свободен' — обозначено единичным битом, а состояние 'занят' — нулевым. Предположим, также, что в исходной бито-последовательности бит с индексом 1 (отсчет с нуля, справа налево по рисунку) установлен в состояние 'занят'. Тогда bitmap_t для такой бито-последовательности будет выглядеть как на рисунке ниже:
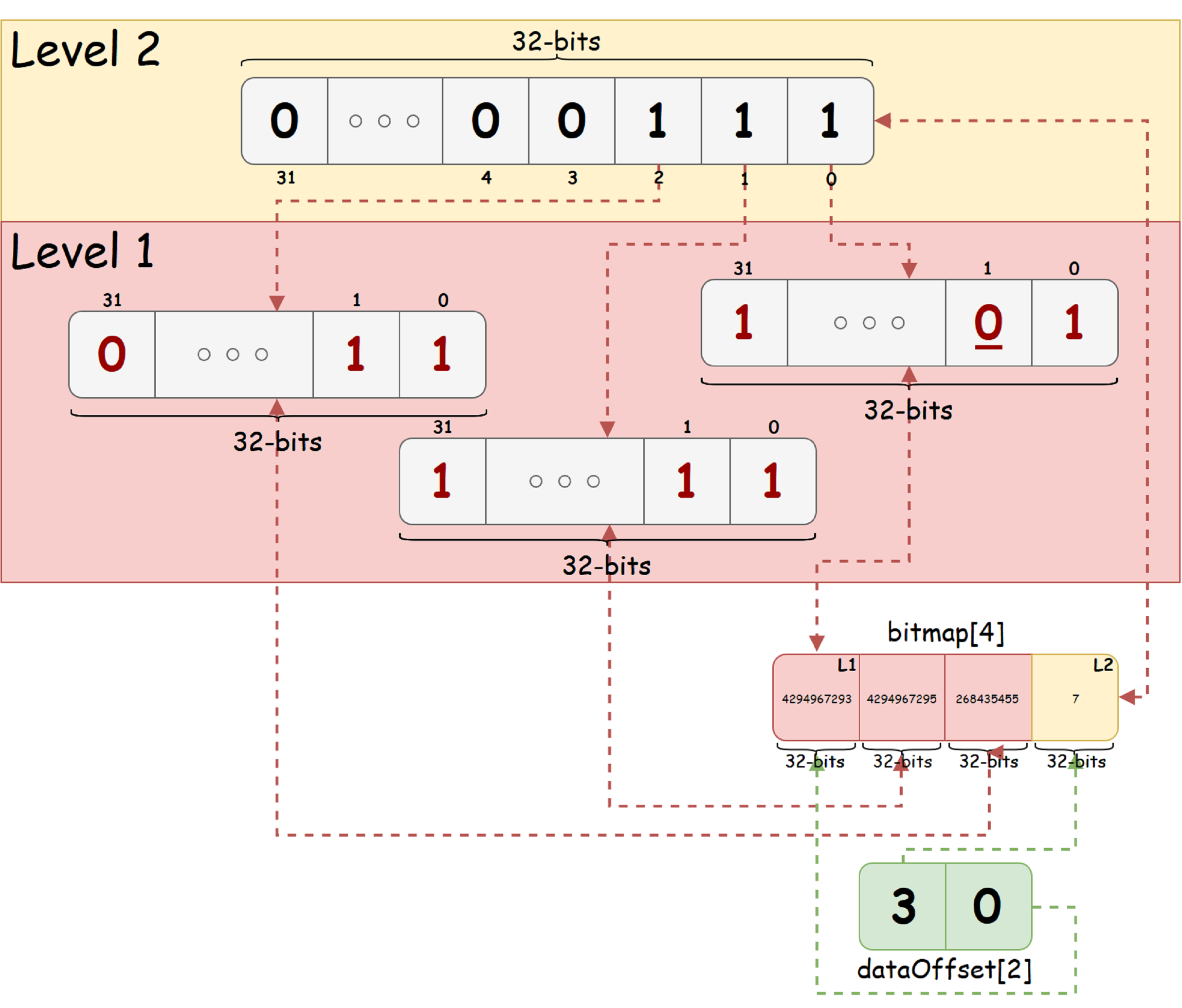
По рисунку видим, что у результирующего дерева всего два уровня. Корневой уровень содержит 3 единичных бита, что свидетельствует о наличии как свободных так и занятых бит в каждом из дочерних узлов соответствующего бита. В правом нижнем углу можно видеть представление Дерева двумя массивами: всех узлов дерева и смещений каждого уровня в массиве узлов.
Полагая, что bitmap_t представлен двумя массивами(массив данных и массив смещения уровней дерева в массиве данных), опишем операцию поиска первого младшего единичного бита в заданном bitmap_t:
- Начиная с корневого узла, выполняем операцию поиска первого младшего единичного бита узла: для решения этой задачи современные процессоры предоставляют специальную инструкцию, позволяющую значительно сократить время поиска. Найденный результат сохраним в переменную FirstSetedBit.
- На каждой итерации алгоритма будем поддерживать сумму позиций найденных бит: countOfSettedBits += FirstSetedBit
- Используя результат прошлого шага перейдем в дочерний узел первого младшего единичного бита узла и повторим предыдущий шаг. Переход осуществляется по следующей незамысловатой формуле:
- Процесс продолжается до тех пор, пока не будет достигнут самый нижний уровень дерева. countOfSettedBits — номер искомого бита во входной последовательности бит.
Pairing Heap — heap-подобная древовидная структура данных, которая позволяет:
- Выполнять вставку элемента с константной временной сложностью — O(1) и амортизированной стоимостью O(log N) или O(1) — в зависимости от реализации.
- Искать минимум за константное время — O(1)
- Выполнять слияние двух Pairing Heap с константной временной сложностью — O(1) и амортизированной стоимостью O(log N) или O(1) — в зависимости от реализации
- Удалять произвольный элемент(в частности минимальный) с временной оценкой сложности в O(N) и амортизированной оценкой сложности в O(log N)
Говоря более формально, Pairing Heap это произвольное дерево с выделенным корнем, удовлетворяющее свойствам кучи(ключ каждой вершины не меньше / не больше, чем ключ её родителя).
Типичная Pairing Heap-а в которой значение дочернего узла меньше значения родительского узла(aka Min Pairing Heap) выглядит как-то так:
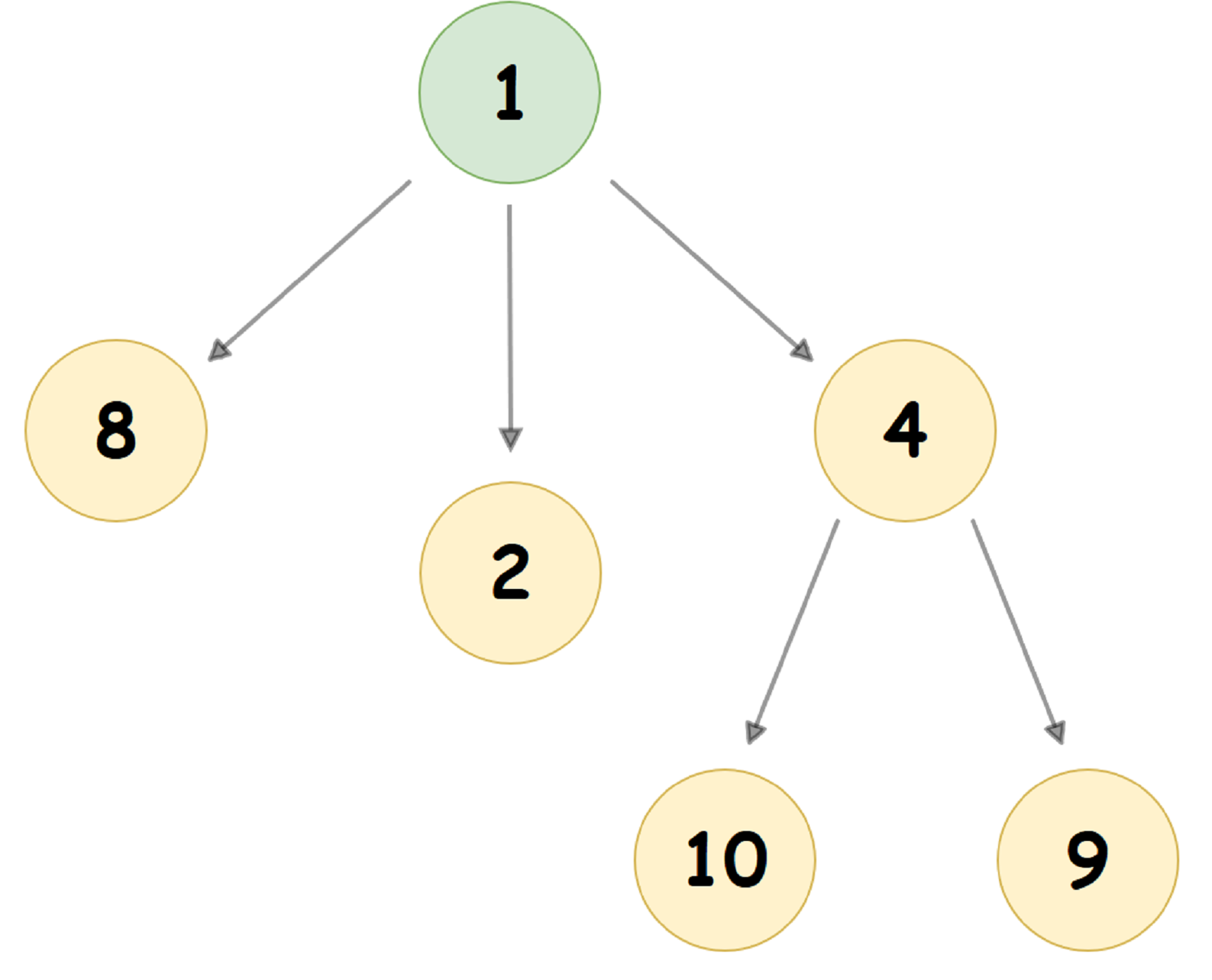
В памяти же компьютера Pairing-Heap, как правило, представлена совсем иначе: каждый узел Дерева хранит 3 указателя:
- Указатель на самый левый дочерний узел текущего узла
- Указатель на левого брата узла
- Указатель на правого брата узла
Если какой-либо из указанных узлов отсутствует, соответствующий указатель узла зануляется.
Для кучи, представленной на рисунке выше мы получаем следующее представление:
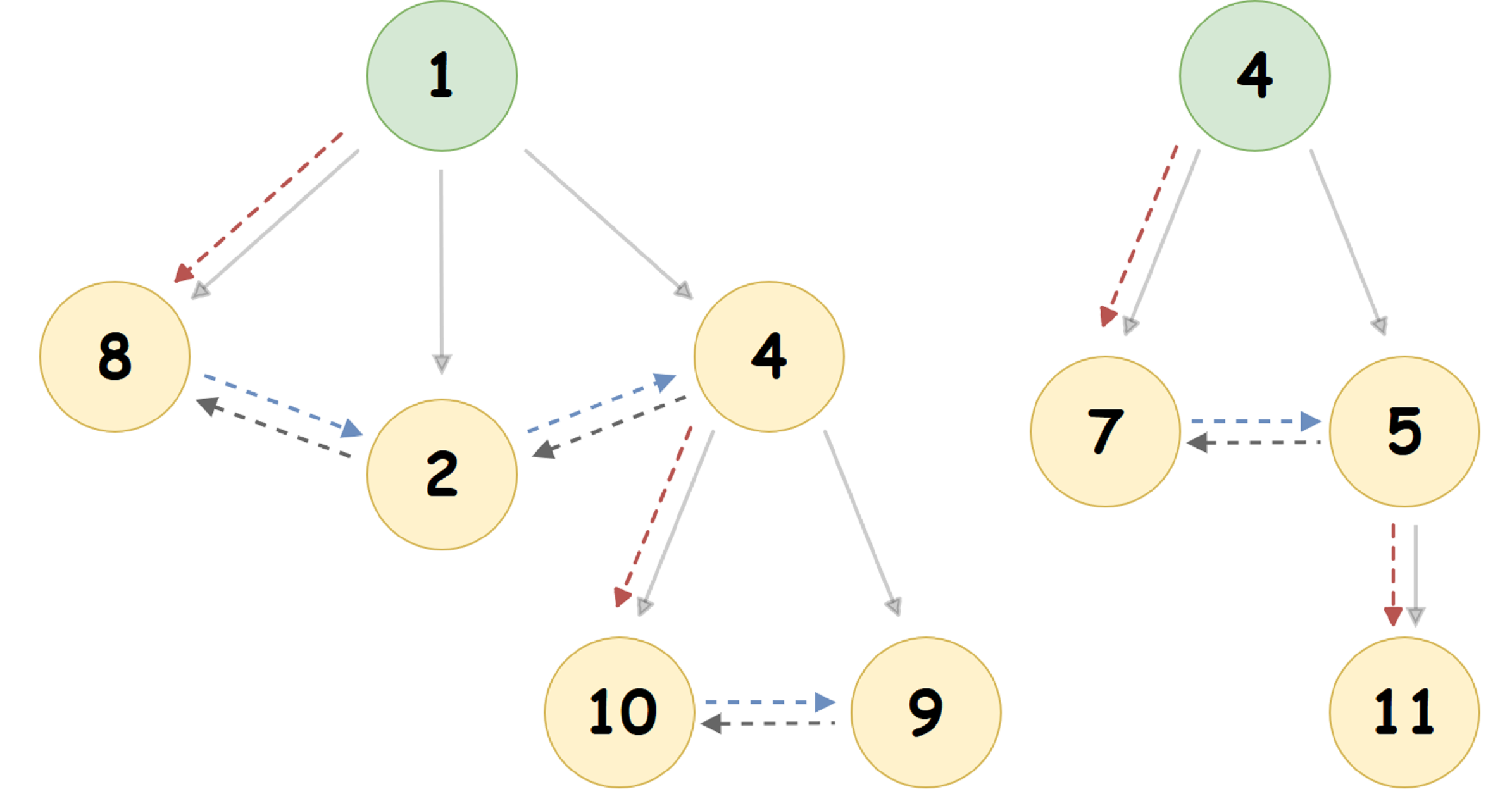
Здесь, указатель на самый левый дочерний узел обозначен красной пунктирной стрелкой, указатель на правого брата узла — синей, а указатель на левого брата — серой. Сплошной же стрелкой показано представление Pairing Heap в обыденном для человека древовидном виде.
Обратите внимание на следующие два факта:
- У корня кучи всегда отсутствуют правый и левый братья.
- Если у какого-либо узла U имеется ненулевой указатель на самый левый дочерний узел, то этот узел будет являться 'Головой' двусвязного списка всех дочерних узлов узла U. Такой список называют siblingList.
Далее, перечислим алгоритм действий основных операций в Min Pairing-Heap-е:
- Вставка узла в Pairing Heap:
Пусть дана Pairing Heap с корнем и значением в нем { R, V_1 }, а также узел { U, V_2 }. Тогда, при вставке узла U в данную Pairing Heap:
- Если условие V_2 < V_1 выполняется: U становится новым корневым узлом кучи, 'вытесняя' корень R в позицию своего левого дочернего узла. При этом, правым братом узла R становится его старый самый левый узел, а указатель на самый левый узел узла R — зануляется.
- Иначе: U становится самым левым дочерним узлом корня R, а его правым братом становится старый самый левый узел корня R.
- Слияние двух Pairing Heap:
Пусть даны две Pairing Heap-ы с корнями и значениями в них { R_1, V_1 }, { R_2, V_2 } соответственно. Опишем один из алгоритмов слияния таких куч в результирующий Pairing Heap:
- Выберем кучу с наименьшим значением в корне. Пусть это будет куча { R_1, V_1 }.
- 'Отсоединим' корень R_1 от выбранной кучи: для этого просто занулим его указатель на самый левый дочерний узел.
- Новым указателем на самый левый дочерний узел корня R_1, сделаем корень R_2. Заметьте, что с этого момента R_2 теряет статус корня и является обычным узлом результрующей кучи.
- Установим правого брата узла R_2: новым значением сделаем старый(до зануления) указатель на самый левый дочерний узел корня R_1, а у R_1, соответственно, обновим указатель на левого брата.
Рассмотрим алгоритм слияния на конкретном примере:
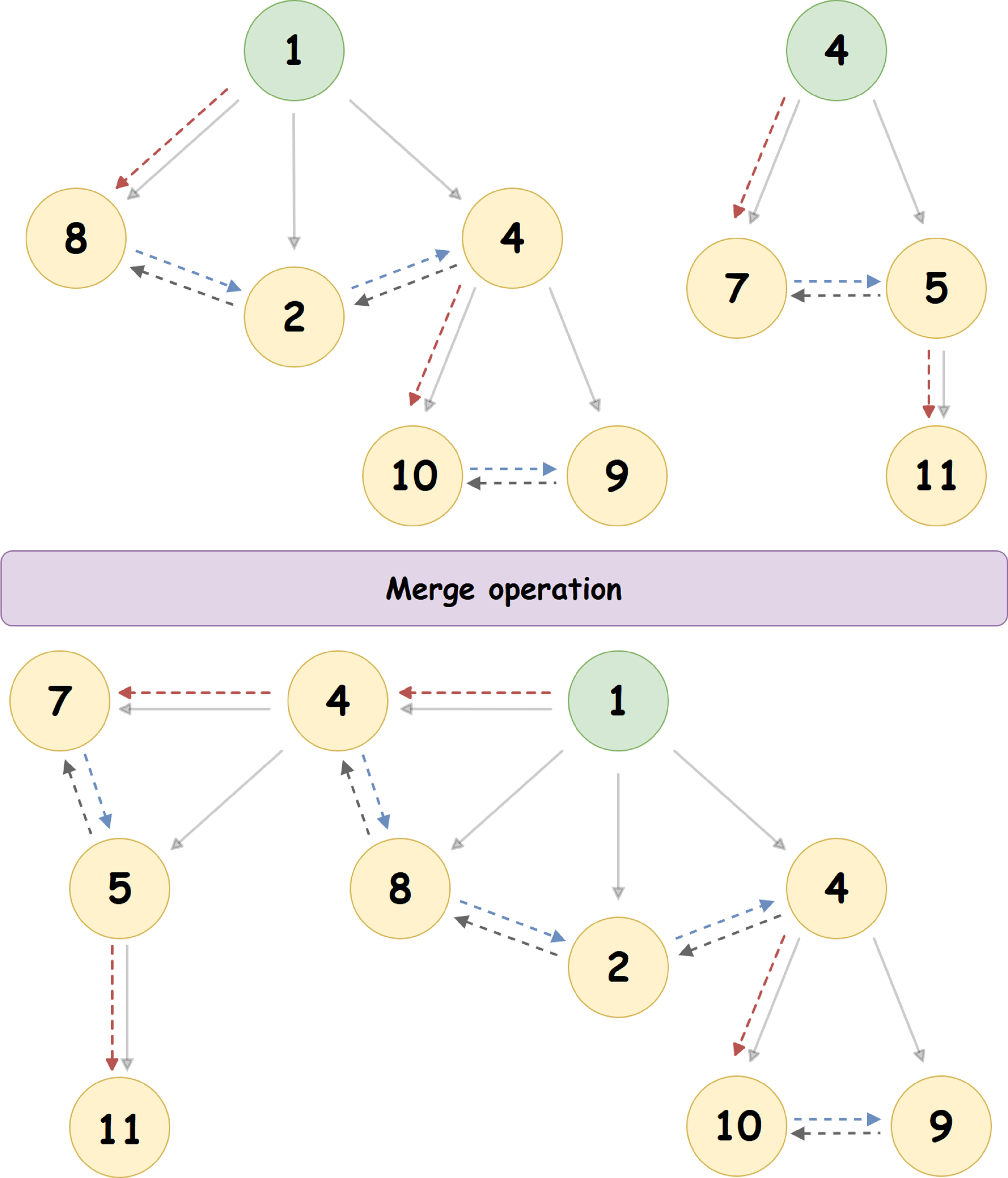
Здесь, куча с корнем '4' присоединяется к куче с корнем '1' (1 < 4), становясь его самым левым дочерним узлом. Указатель на правого брата узла '4' — обновляется, как и указатель на левого брата узла '8'.
- Удаление корня(узел с минимальным значением) Pairing Heap:
Существует несколько алгоритмов удаления узла из Pairing Heap, гарантировано дающих амортизированную оценку сложности в O(log N). Опишем один из них, именуемый multipass алгоритмом и используемый в JeMalloc:
- Удалим корень заданной кучи, оставив только его самый левый дочерний узел.
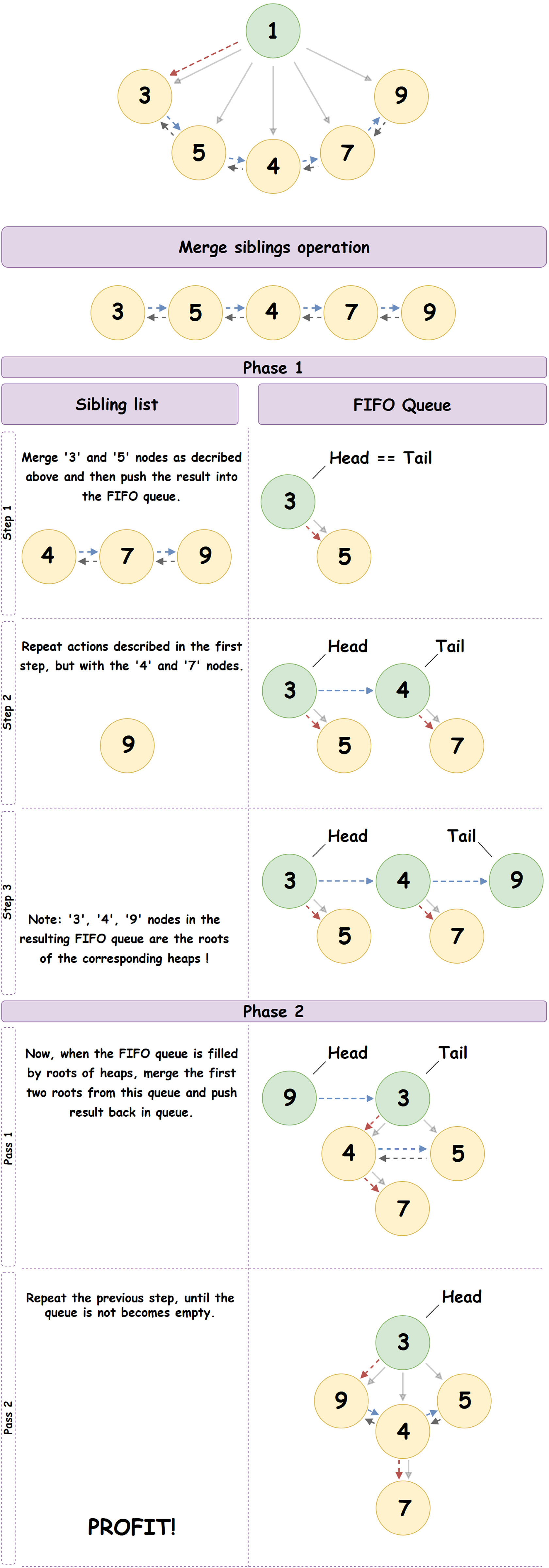
- Самый левый дочерний узел образует двусвязный список всех дочерних узлов родительского узла, а в нашем случае — ранее удаленного корня. Будем последовательно идти по этому списку до конца и, рассматривая узлы как корни независимых Pairing Heap, выполнять операцию слияния текущего элемента списка со следующим, помещая результат в заранее заготовленную FIFO очередь.
- Теперь, когда FIFO очередь инициализирована, будем итерироваться по ней, выполняя операцию слияния текущего элемента очереди со следующим. Результат слияния помещаем в конец очереди.
- Повторяем предыдущий шаг до тех пор, пока в очереди не останется один элемент: результирующий Pairing Heap.
Наглядный пример процесса описанного выше:
- Удаление произвольного не корневого узла Pairing Heap:
Рассмотрим удаляемый узел как корень некоторого поддерева исходной Кучи. Сначала удалим корень этого поддерева, следуя ранее описанному алгоритму удаления корня Pairing Heap, а затем, выполним процедуру слияния полученного дерева с исходным. - Получение минимального элемента Pairing Heap:
Просто возвращаем значение корня кучи.
Однако, на этом наше знакомство с Pairing Heap не заканчивается: Pairing Heap позволяет выполнять некоторые операции не сразу, а только тогда, когда возникает необходимость в них. Иными словами Pairing Heap позволяет выполнять операции 'Лениво', тем самым понижая амортизированную стоимость некоторых из них.
Положим, мы сделали K вставок и K удалений в Pairing Heap. Очевидно, что результат выполнения этих операций становится нужен лишь тогда, когда мы запрашиваем у кучи минимальный элемент.
Рассмотрим как поменяется алгоритм действий описанных ранее оперций при их Ленивой реализации:
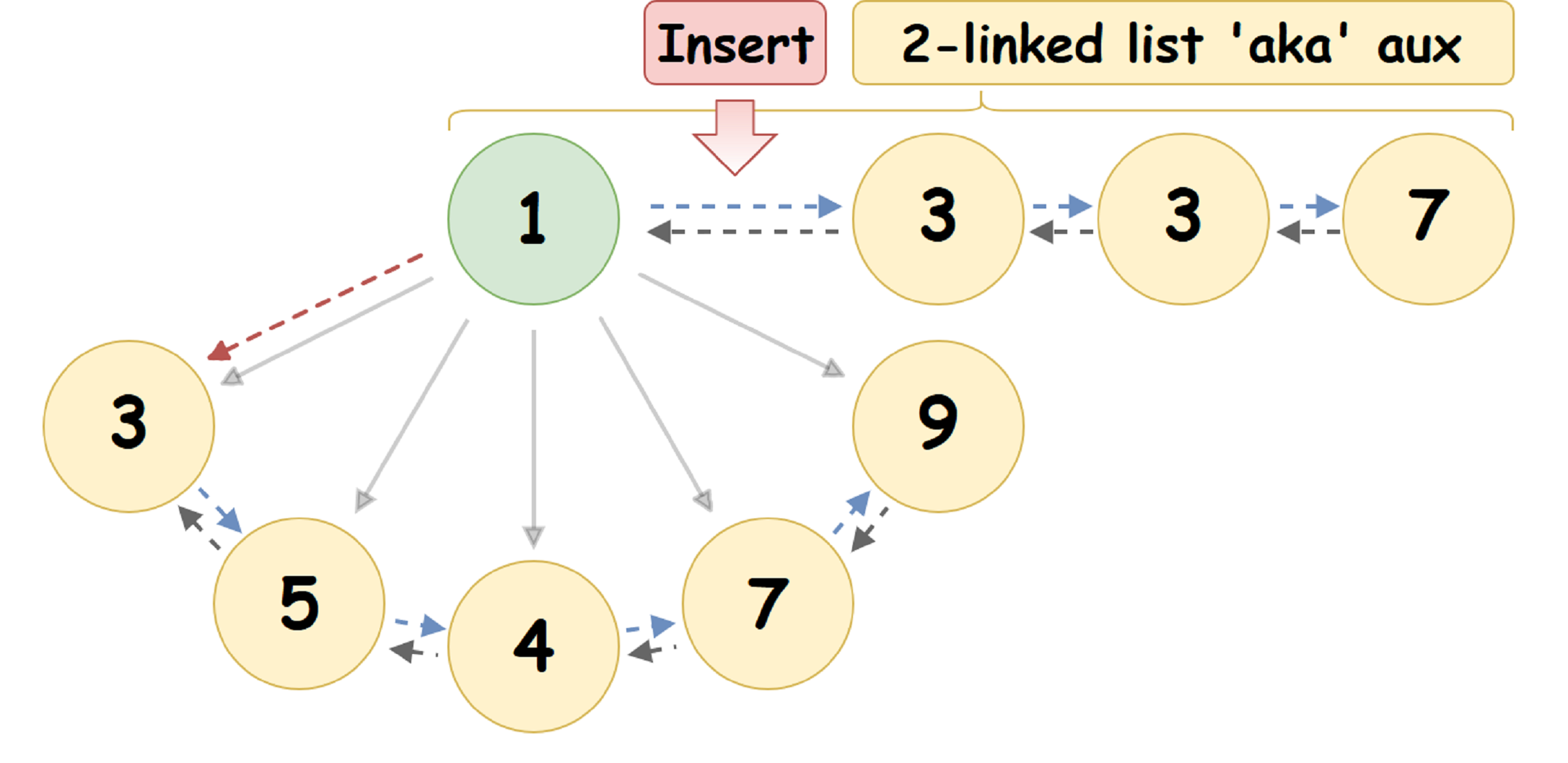
Пользуясь тем, что корень Кучи имеет как минимум два нулевых указателя, будем использовать один из них для представления головы двусвязного списка (далее auxList) вставляемых в кучу элементов, каждый из которых будем рассматривать как корень независимой Pairing Heap. Тогда:
- Ленивая вставка узла в Pairing Heap:
При вставке заданного узла U в Pairing Heap { R_1, V_1 }, помещаем его в auxList — после головы списка:
- Ленивое слияние двух Pairing Heap:
Ленивое Слияние двух Pairing Heap, аналогично Ленивой втавке узла, где вставляемый узел — корень(голова двусвязного auxList) одной из куч. - Ленивое получение минимального элемента Pairing Heap:
При запросе минимума, проходим по auxList списку корней независмых Pairing Heap, попарно объединяя элементы этого списка операцией слияния, и возвращаем значение корня, содержащего минимальный элемент, одной из результирующих Pairing Heap. - Ленивое удаление минимального элемента Pairing Heap:
При запросе удаления минимального элемента заданной Pairing Heap, сначала находим узел содержащий минимальный элемент, а затем, удаляем его из дерева в котором он является корнем, вставляя его поддеревья в auxList основной кучи. - Ленивое удаление произвольного некорневого узла Pairing Heap:
При удалении произвольного некорневого узла Pairing Heap, узел убирается из кучи, а его дочерние узлы вставляются в auxList основной Кучи.
Собственно, использование Ленивой реализации Pairing Heap, снижает амортизированную стоимость операций вставки и удаления проивольных узлов в Pairing Heap: с O(log N) до O(1).
На этом все, а ниже ты найдешь список полезных ссылок и ресурсов:
[0] JeMalloc Github Page
[1] Оригинальная статья о Pairing Heaps
[2] Оригинальная статья о Lazy Implementation Pairing Heaps
[3] Телеграмм канал о оптимизациях кода, С++, Asm, 'низкоуровщине' и только, только о этом!
Продолжение следует…


kyprizel
Спасибо, недавно обнаружил столь крупные изменения в jemalloc между версиями 4.x и 5.x, а здесь ваша статья. Ждем продолжения.