Число, лежащее в основе современной музыки / forpes.ru

Главная
Число, лежащее в основе современной музыки

Число, лежащее в основе современной музыки +55

15.10.2019 16:24

nihole 301 27600 Источник

Почему двенадцать?

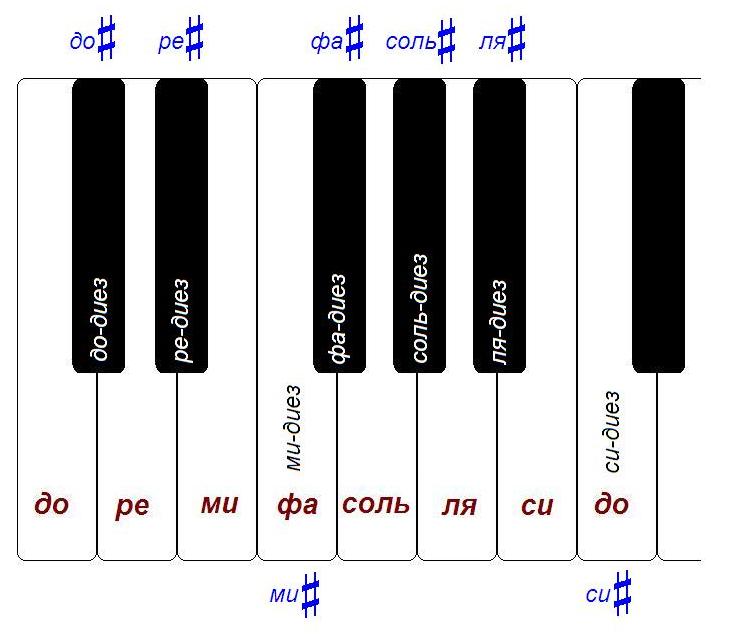
Если вы посмотрите на клавиатуру, то увидите, что в каждой октаве содержится 12 полутонов.
В случае фортепиано это всего лишь значит, что между, например, "до" первой октавы и "до" второй октавы расположено 11 клавиш. Вместе с одним из "до" (например, до второй октавы) мы получим 12 клавиш: до#, ре, ре#, ми, фа, фа#, соль, соль#, ля, ля#, си, до.

Но почему 12?

Может быть это просто случайность? Вот нравилось нашим предкам число 12, у них везде 12: 12 месяцев, 12 знаков зодиака, 12 колен Израилевых, 12 апостолов,… и здесь решили, пусть будет 12, и так и повелось. Или все же здесь есть объективный закон, и это число не случайно?

В этой статье я попытаюсь продемонстрировать, что это не случайность. Достаточно общие требования, вполне естественные для современной (западной) музыки, с математической необходимостью приводят нас к числу 12. Интересно, что причиной почему у нас появляется это значение является свойство другого числа (см. в конце статьи). Можно даже сказать, что оно то и лежит в основе современного звучания.

Постановка задачи

Сначала давайте попробуем формализовать задачу.

У нас есть опорная частота $\omega_0$ . Будем называть ее тоникой. У нас также есть октава с частотой $2\omega_0$ . Теперь мы должны понять, какие могут быть варианты промежуточных частот от $\omega_0$ до $2\omega_0$ , такие, чтобы мелодия, построенная на этих нотах, звучала бы для нашего слуха гармонично?

Боюсь, что эта формулировка, хотя и отражает суть вопроса, все же, с математической точки зрения, является довольно туманной, и на такой вопрос не может быть однозначного ответа, хотя бы потому, что человеческий слух имеет довольно ограниченную разрешающую способность по частоте. И это подтверждается тем, что в разное время использовались разные строи, например, пифагоров, чистый, хорошо темперированный, равномерно темперированный строи. И все они звучали и звучат, как минимум для определенных произведений, вполне приемлемо.

Что такое гармония?

Мы должны наложить некоторые дополнительные условия. Но прежде мы должны ответить на один важный вопрос: что мы воспринимаем как гармоничное звучание?

Давайте рассмотрим два звука — с частотами $\omega_1$ и $\omega_2$ .

Возьмем отношение этих частот. Это отношение можно представить в виде произведения чисел $a_1^{k_1}\cdot a_2^{k_2}\cdot...\cdot a_l^{k_l}$ , где $inline$ — простые числа, а $inline$ — целые числа, например, это отношение может равняться $2^{-3}\cdot3\cdot5$ . И чем эти простые числа ( $inline$ ) меньше, тем гармоничнее для нашего уха будет звучать этот интервал (я нашел это утверждение тут (см. второй абзац))

Так, например, самым гармоничным звучанием в соответствии с этим утверждением будет являться октава (изменение частоты в 2 раза). А следующими по гармоничности интервалами будут квинта (изменение частоты в $inline$ раза) и кварта (изменение частоты в $inline$ раза).

Но не так все просто с этим утверждением. Так, например, не очень понятно, как влияет степень. Например, что гармоничнее умножение на $inline$ или на 7? Я не знаю, изучен этот вопрос или нет, и можно ли в принципе дать на него ответ. Также восприятие гармоничности — вещь довольно субъективная. Так, современная музыка полна звучаний, которые 100 — 200 лет были бы восприняты не иначе как жуткая какофония.

Условие первое. Тоника, кварта, квинта, октава

Эта неопределенность не является проблемой для нашего маленького исследования. Дело в том, что единственный вывод, который я хочу сделать из этого утверждения заключается в том, что в нашем строе в любом случае должны быть как минимум "самые гармоничные" интервалы, а именно, октава, кварта и квинта. То есть наряду с тоникой с частотой $\omega_0$ и октавой с частотой $2\omega_0$ у нас также должны быть квинта и кварта, с частотами соответственно ${3\over 2}\omega_0$ , ${4\over 3}\omega_0$ или что-то очень близкое, что мы не смогли бы отличить от чистой квинты и кварты.

И это наше первое требование.

Условие второе. Инвариантность

Вторым нашим требование будет инвариантность. И это важное требование современной музыки. Заключается это требование в том, что все гармонии в любых тональностях должны звучать одинаково. Если мы говорим про современный строй, который применяется при настройке фортепиано, то это значит, что квинта, состоящая из семи полутонов, должна звучать одинаково, независимо от того, от какого звука она построена. То есть соотношение частот между до и соль должно быть таким же как и для до# — соль#, ре — ля, ре# — ля#,… и равняться $inline$ . И эта инвариантность должна относиться, конечно, не только к квинте, но и к любым интервалам. Важным преимуществом этого строя является возможность транспонирования пьесы на любой интервал. В этом и заключается суть равномерной темперации.

Нужно сказать, что это требование инвариантности не является таким очевидным, и данный подход был применен относительно недавно, лишь в 18 веке. Строи, применявшиеся до этого, (например, пифагоров и чистый) не обладали таким свойством. Вот послушайте, например, Sonata for Microtonal Piano (Ben Johnston), написанную в чистом строе (prime limit = 5). Такое ощущение, что фортепиано не настроено. Все богатство современных гармоний основано именно на этой инвариантности. Например, "Хорошо темперированный клавир" Баха появился именно благодаря новому подходу в настройке клавишных. Именно вот эта инвариантность дала возможность Баху создавать гармонические последовательности, которые просто были невозможны раньше.

Итак, теперь мы имеем все необходимые для расчета данные.

Расчет

Давайте построим звукоряд от тоники до октавы, который бы удовлетворял обоим требованиям.
Предположим, что в этом случае мы получим $inline$ звуков (включая октаву). Это $inline$ и является искомым числом. Мы хотим показать, что $inline$ при наших условиях должно равняться 12.

Следствием второго требования является то, что интервал между частотами соседних звуков должен быть одинаковым и должен быть равен $2^{1\over N}$ .

Теперь первое требование говорит о том, что в нашем ряду должны быть два звука, соответствующие (с хорошим приближением) частотам ${3\over 2}\omega_0$ и ${4\over3}\omega_0$ . Это квинта и кварта. Предположим, что кварта это $inline$ -ый звук в нашем ряду, а квинта — $inline$ -ой. Обозначим $inline$ .

Нетрудно видеть, что изменение частоты между квартой и квинтой (отношение частот) равно $inline$ .

Но, в соответствии с нашим вторым условием, это также должно быть равно $2^{n\over N}$ .

Итак, мы получили формулу:

$2^{n\over N} \approx 9/8$

После несложных преобразований получим основную формулу:

$n \approx N(2\log_2 {3} - 3) = N\cdot 0,170$

Легко увидеть, что решением (конечно, приблизительным) является $inline$ , где $inline$ — любое натурально число (достаточно малое, потому что все же 0,170 отличается от 1/6).

Давайте рассмотрим случай $inline$ . В этом случае $inline$ , $inline$ . То есть, это вариант современного строя, только без полутонов, только с тонами (до, ре, ми, фа#, соль#, ля#, до). Но, как вы видите, в этом случае кварта (фа) и квинта (соль) в этот звукоряд не попали.

То есть единственным вариантом для нас может быть

$inline$ , где $inline$ — любое натурально число ( $inline$ достаточно малое). Случай $inline$ как раз и соответствует нашему современному строю, который называется равномерно темперированный строй.

Но почему не 24 или большее число? Причина проста — могу предположить, что такая градуированность уже является излишней для нашего восприятия. Поэтому остается только одно число: 12.

Заключение. Число, лежащее в основе

Удивительно, но получается, что числом, лежащим в основе современного музыкального строя и современной (европейской) музыки, является $\log_2{3}$ , а именно то, что с хорошей точностью (0,1%) выполняется следующее равенство:

$\log_2 {3} \approx 19/12$

Комментарии (301)

humbug
15.10.2019 20:10
#20759574
+12
Но почему не 24, 36, 48…? Причина проста — наш слух уже не различает этой градуированности. Поэтому остается только одно число: 12.
О да, конечно не различает)))
Sirion
15.10.2019 21:17
#20759930
+5
Как давний подписчик паблика с микротональной музыкой, зашёл написать этот комментарий, а он уже написан.

mi_bag
16.10.2019 01:13
#20761018
А не знаете, есть ли примечательные примеры? Которые не просто играются на неизведанной территории, а хорошо продуманы, ну и, скажем, не этническая музыка.
И кроме упомянутого в видео «Lo-Fi Hip Hop» радио.

Есть, кстати, другая сторона микротональности — точное интонирование, когда выходят за рамки 12 полутонов для построения правильных гармоний. Хороший пример — вундеркинд от музыки Jacob Collier, его композиции могут звучать непривычно, при том что, наоборот, используют математически правильные интервалы! И интервью с ним иногда очень удивляют.

naething
16.10.2019 08:49
#20761774
Альбом «Flying Microtonal Banana» от King Gizzard and the Lizard Wizard.

www.youtube.com/watch?v=Q-i1XZc8ZwA

SADKO
16.10.2019 12:30
#20763150
Да у них и в других альбомах, тут просто в названии упомянули микротональность.

Ещё можно у Brendan Byrnes альбом Micropangaea послушать, он конечно не без заходов на территорию, но продуман хорошо…

И ещё турки, Tolgahan Cogulu & Sinan Cem Eroglu — Microtonal Guitar Duo, не без этники но многие вещи звучат вполне себе по европейски…

iShrimp
16.10.2019 19:28
#20765642
Пожалуйста, сейчас я вам накидаю ссылок.
Исполнитель: Gary Garrett. Песня в натуральном строе, с наглядной визуализацией всей гармонии: Flying Dream https://youtu.be/jA1C9VFqJKo
Исполнитель: Dolores Catherino. Композиция Towards the Continuum, служащая "мостом" от стандартного строя 12edo к континууму. Клавиатура Tonal Plexus, 106 ступеней в октаве. https://youtu.be/8re6rFj7q10
Исполнитель: Brendan Byrnes. Красивая игра на 22-ступенной гитаре. https://youtu.be/qHHv3mwJTlg

nihole Автор
15.10.2019 21:39
#20760088
+1
Как видите с математической точки зрения может быть и 24 и 36 и 48 при тех же 2х условиях, которые были сформулированы.
Я не имел ввиду то, что мы не различаем что-то меньше, чем малая секунда. Конечно, различаем. Некоторые люди с абсолютным слухом могут сказать вам что звучит с точностью до 1/8 тона. Я скорее предположил, что это различие уже настролько несущественно и градуировано, что может служить лишь как некоторая окраска, как некие вспомогательные звуки (как в случае индийской музыки), но не как основные звуки.

Впрочем, это утверждение не явлется столь важным. Если хотите, то можно говорить о 12 и о 24.

humbug
15.10.2019 22:34
#20760382
+2
Некоторые люди с абсолютным слухом могут сказать вам что звучит с точностью до 1/8 тона.
Чтобы различать 1/8 тона требуется развитый относительный(интервальный) слух, а не абсолютный. И развивается точность в 1/8 за 3-5 лет сольфеджио. То есть это по силам практически всем заинтересованным лицам, правда я не понимаю зачем им это может понадобиться.

jahma48
16.10.2019 12:34
#20763172
отличная статья! конечно различаем меньше малой секунды, и очень неплохо, просто мелодических канонов для такой ткмперации нет или они не распространены. и последние несколько сотен лет развиваемся таким образом, чтобы музыка, основанную именно на таком строе, нам было приятно и «удобно» слушать. как академический музыкант до мозга костей, к микротональной музыке отношусь скептически, эдакий творческий фаллоимитатор — когда ты бессилен в октаве из 12 нот, начинаешь лепить франкенштейна из 19, выдавая за высокое искусство, к которому человечество еще не готово. И получается, как в том анекдоте:

Стоит чувак в галерее напротив картины:
— Какое буйство красок! Какое… легкость линий! Какая… чистота мазков!
К нему подходит другой и спрашивает:
— Я извиняюсь, а вы когда-нибудь е*али ежа?
— Нет конечно, а почему вы спрашиваете??
— Да я смотрю вы какую-то херню несете, и я решил что-то спи*дануть

стоит чувак в галерее напротив картины:

math_coder
16.10.2019 15:53
#20764438
как академический музыкант до мозга костей
А из Дмитрия Курляндского можете сыграть что-нибудь поинтереснее? "Прерванную память", например, или "Riot of spring"? Это академическая музыка для академических музыкантов.

0xd34df00d
16.10.2019 19:30
#20765646
эдакий творческий фаллоимитатор — когда ты бессилен в октаве из 12 нот, начинаешь лепить франкенштейна из 19, выдавая за высокое искусство, к которому человечество еще не готово
Я так всякий техникал металкор научился слушать. Первый-второй раз слушаешь — ужас, какофония какая-то, ритма нет, ничего не понятно. А потом как-то приучаешься.

iShrimp
16.10.2019 20:05
#20765804
Надмножества строя 12edo, конечно, удобны тем, что они делят ступени 12edo на равные части. Но всё-таки, если рассмотреть ряд 12edo, 24edo, 36edo и т.д., то с уменьшением ступени относительная погрешность только растёт, и они всё хуже выполняют свою задачу — аппроксимацию натуральных гармоник.
Тут нужен другой математический подход. Пусть x — число ступеней в октаве. Для каждого из базовых интервалов (2/1, 3/1, 5/1 и т.д.) желательно, чтобы в него умещалось целое число ступеней. Построим функцию от х, значение которой тем выше, чем лучше аппроксимируются наши интервалы:
f(x) = cos(2?x) + cos(2?x log(3)/log(2)) + cos(2?x log(5)/log(2)) + cos(2?x log(7)/log(2)) +…
Если взять последовательные максимумы данной функции, то получится множество оптимальных делений октавы.
Также можно почитать о поиске равномерных строёв на Xenharmonic Wiki: https://en.xen.wiki/w/The_Riemann_Zeta_Function_and_Tuning

ingumsky
15.10.2019 22:37
#20760396
О! Вышнеградский упоминается! :)

Теперь я понял, как получается звучание, которое я раньше знал по Клатчи Хопкинсу.

nihole Автор
15.10.2019 23:48
#20760744
Снизил степерь категоричности в статье. Спасибо!

mwizard
15.10.2019 20:18
#20759620
+5
Единственно возможный? Расскажите китайцам и всяким арабам, что пентатоника, их музыкальный лад, невозможна.
1. epishman
  15.10.2019 21:33
  #20760050
  А я всегда думал что пентатоника из диатоники вытекает, просто отбрасываем малые секунды.
  1. lair
    15.10.2019 21:35
    #20760064
    +1
    "Пентатоника — самодостаточная и полная интервальная система; ангемитоновый пятиступенный звукоряд не следует трактовать как диатонический с «пропущенными» ступенями."
    
    nihole Автор
    15.10.2019 21:42
    #20760102
    Мне кажется, что ясно показано, что если у нас есть 2 условия (сформулированные в статье), то может быть лишь 12, 24, 36…
    Если вы утверждаете что существует что-то еще, то значит это не соответствует этим 2м условиям и скорее всего это условие инврариантности. Стоев без инавериатности огромное количество, точнее все, которые не являются равномерно темперированными.
    
    lair
    15.10.2019 21:43
    #20760116
    -1
    … и как это связано с комментарием, на который вы отвечаете?
    
    nihole Автор
    15.10.2019 21:52
    #20760174
    а почему вы говорите про пентатонику?
    
    lair
    15.10.2019 22:25
    #20760326
    Потому что человек в комментарии, на который я отвечаю, говорит про пентатонику.
    
    nihole Автор
    15.10.2019 22:04
    #20760214
    >Расскажите китайцам и всяким арабам, что пентатоника, их музыкальный лад, невозможна.
    Я не говорил про невозможность. Кроме равномерно темперированного строя существует много других строев. Что в них невозможно, так это модуляция.
    
    math_coder
    15.10.2019 22:15
    #20760268
    +1
    А по-моему, говорили:
    
    12 является единственно возможным вариантом в современном музыкальном строе
    
    nihole Автор
    15.10.2019 22:41
    #20760418
    Наверно, каждый под словом современная музыка подразумевает свое.
    
    Я воспитан на западной музыке. На классической музыке и джазе, во многом опирающемся на гармонии классической музыки. Я люблю Баха, например, и его музыку, его гармонии я считаю основой СОВРЕМЕННОЙ музыки.
    
    Может быть было бы правильно добавить слово европейской. Может быть.
    
    Но если вы под современной музыкой подразумеваете музыку, построенной на пентатонике или например пифагоровом строе или каком-нибудь современном, необычном микротонике, то у нас с вами очень разный бэкграунд.
    
    В статье же описаны 2 требования, которые я считаю являются необходимыми для того, что я подразумеваю под современной музыкой. И так же я говорю в статье что существуют другие строи.
    
    И в статье на самом деле главное математика.
    Там сформулирована задача. Описано почему такие требования и задача решена.
    
    math_coder
    15.10.2019 23:42
    #20760712
    +1
    Но если вы под современной музыкой подразумеваете музыку, построенной на <...> каком-нибудь современном
    Да, и в самом деле странно такое подразумевать...
    
    ingumsky
    16.10.2019 09:15
    #20761906
    Я так понимаю, речь о западной музыке, которая на нём построена. Автор статьи говорит, что в контексте этой музыки другой строй невозможен.
    
    lair
    16.10.2019 11:16
    #20762654
    +1
    Автор статьи говорит, что в контексте этой музыки другой строй невозможен.
    Это именно та кольцевая логика, про которую я и говорю: если выбрать музыку, построенную на определенном строе, очевидно, что в ее контексте другой строй невозможен.
    
    ingumsky
    16.10.2019 11:49
    #20762862
    Кому именно очевидно? Вам очевидно, кругу комментаторов здесь очевидно или всем очевидно? С точки зрения обывателя, существует 7+5 нот, на которых построена «вся» музыка. И для него как раз вовсе не очевидно, как получается, что есть музыка других культур или музыка того же Вышнеградского сотоварищи, в которой используются «фальшивые» ноты, но которая при этом звучит мелодично, хотя и «странновато». И почему те же ноты звучат именно что фальшиво или, как минимум, очень странно, если попытаться их использовать в «обычной» музыке.
    
    lair
    16.10.2019 11:56
    #20762902
    +2
    Кому именно очевидно?
    Человеку, который прочитает фразу "в контексте музыки, построенной на строе Х, невозможен строй, отличный от Х".
    
    И для него [обывателя] как раз вовсе не очевидно, как получается, что есть музыка [...] в которой используются «фальшивые» ноты, но которая при этом звучит мелодично, хотя и «странновато». И почему те же ноты звучат именно что фальшиво или, как минимум, очень странно, если попытаться их использовать в «обычной» музыке.
    Ну во-первых, я не думаю, что обыватель об этом вообще задумывается, извините за прямоту. Слушать музыку можно и без этого.
    
    А во-вторых, статья, полностью игнорируя музыку других культур, как раз и не дает ответа на этот вопрос.
    
    lair
    15.10.2019 22:27
    #20760336
    Что в них невозможно, так это модуляция.
    Это, очевидно, неправда. В барочной музыке модуляции предостаточно, а равномерного строя там нет.
    
    И вы в любом случае отвечаете не тому человеку.
    
    grayfolk
    16.10.2019 02:33
    #20761126
    +1
    В барочной музыке модуляции предостаточно, а равномерного строя там нет.
    
    К слову, как я понимаю, они ограничены тональностями первой (возможно, максимум второй) степени родства, потому что при более далеких модуляциях отсутствие равномерно темперированного строя приведет к заметной фальши.
    
    lair
    16.10.2019 02:49
    #20761132
    Только на инструментах с фиксированной темперацией (да и там можно подобрать строй под произведение, или написать произведение с расчетом на конкретный строй).
    
    Но, на самом деле, ничего такого ужасного в ограничении на тональности для модуляции нет, это всего лишь еще одно из множества инструментальных ограничений, которые можно побороть в обмен на что-нибудь другое.
    
    lair
    16.10.2019 11:46
    #20762846
    Мне кажется, что ясно показано, что если у нас есть 2 условия (сформулированные в статье), то может быть лишь 12, 24, 36… Если вы утверждаете что существует что-то еще, то значит это не соответствует этим 2м условиям и скорее всего это условие инврариантности.
    Это не так. Посмотрим на эти условия еще раз.
    
    Первое требование: звукоряд должен содержать, помимо основания (с высотой x), ступени с высотами 2х, 4x/3 и 3x/2.
    
    Второе требование: все расстояния между соседними ступенями должны быть равны.
    
    Второму требованию удовлетворяет любой равномерно темперированный строй, и он же удовлетворяет требованию на наличие ступени 2x.
    
    Остается найти такой равномерно темперированный строй, в котором будут существовать еще и ступени 4x/3 и 3x/2.
    
    Автор предлагает использовать для этого формулу 2^(n/N) ~ 9/8 (где n — число ступеней между 4x/3 и 3x/2, а N — число ступеней в звукоряде); я (логично, я надеюсь) полагаю, что для этого надо решать задачу минимизации |2^(n/N) — 9/8|. Я недостаточно знаю математику, чтобы решать ее как есть, но зато я могу просто подставить в нее значения и посмотреть, что получается.
    
    Начнем с предлагаемого автором 12-ступенного строя. N = 12, n = 2, |2^(n/N) — 9/8| = 2.537952e-03
    
    Окей, возьмем 58-ступенный строй: N = 58, n = 10, |2^(n/N) — 9/8| = 1.942411e-03. Упс, мы нашли строй, удовлетворяющий всем условиям задачи (что бы я про эти условия ни думал), и число ступеней в котором не делится на 12 нацело.
    
    Что-нибудь не такое страшное? 41 ступень: N = 41, n = 7, |2^(n/N) — 9/8| = 6.292375e-04. Результат даже лучше. 53 ступени: N = 53, n = 9, |2^(n/N) — 9/8| = 8.864364e-05.
    
    Что там говорили про то, что условиям задачи удовлетворяет только 12i?
    
    nihole Автор
    16.10.2019 13:53
    #20763690
    Вы пишите об очевидных вещах. Конечно, т.к. равенство лишь приблизительное, то при больших числах накапливается ошибка.
    Так, например, то что вы написали является всего лишь следствием того, что 0,170 это не 1/6. И конечно при больших i это отличие становится существенным.
    
    Вы действительно все еще пытаетесь найти математическую ошибку в рассуждении?
    
    lair
    16.10.2019 13:56
    #20763696
    Вы пишите об очевидных вещах.
    Если то, о чем я пишу, очевидно, то почему вы утверждаете, что остается только одно число, хотя очевидно, что их больше одного?
    
    Вы действительно все еще пытаетесь найти математическую ошибку в рассуждении?
    Не просто пытаюсь, а нашел.
    
    nihole Автор
    16.10.2019 13:57
    #20763704
    -1
    вы не знаете что такое приблизительно и как накапливается ошибка?
    
    lair
    16.10.2019 14:01
    #20763728
    Я знаю, что такое "приблизительно", и не понимаю, почему вы считаете, что ваше приближенное значение лучше любого другого.
    
    nihole Автор
    16.10.2019 15:01
    #20764094
    да нет, не считаю
    но такой результат дает математика
    
    lair
    16.10.2019 15:06
    #20764134
    Неа, не дает. Математика всего лишь говорит нам, какова разница между нужным нам чистым интервалом и интервалом в такой-то системе, а вы уже говорите, какая разница вас устраивает, а какая — нет.
    
    nihole Автор
    16.10.2019 13:59
    #20763716
    ок, тогда отдельно для вас. Все это справедливо для малых i.
    
    lair
    16.10.2019 14:01
    #20763732
    Для "малых i" в какой формуле? Что "это" справедливо?
    
    (ну то есть на самом деле в вашей системе не два требования, а три?)
    
    nihole Автор
    16.10.2019 14:26
    #20763888
    Хорошо. Давайте еще раз. Смотрите, мы получили число 0,170. На самом деле — это тоже приближение до 3 го знака. На самом деле это число иррациональное. И нам нужно его умножить на целое число, чтобы получить опять таки целое число. Т. к. это число иррациональное, то в любом случае нет такого целого числа. Поэтому все наши рассчеты приблизительны. И вот первое такое целое число очевидно 6. Но если мы умножит 0,170 на 6 то получим 1,02. Не 1, а 1,02. Но это выглядит вполне приемлимо. Таким образом N = 6 удовлетворяет уравнению, но при этом мы «перепрыгиваем» через квинту (и кварту) — почитайте объяснение в статье почему. Поэтому 6 не подходит. Следующее число очевидно 12. Но при это ошибка уже 0,04. Оно нам подходит. Потом 18 — опять перепрыгиваем через квинту и кварту. Не подходит. Поэтому следующее подходящее — 24. При этом ошибка уже 0,08. Дальше при 36 — ошибка 0,12, а при 48 — 0,16 — уже близко к 0.170 поэтому лучше использовать 47.
    
    Это очевидно. Это не отменяет что в основе лежит 12. Просто так как это все приблизительно, то да, при больших числах мы уже должны учитывать ошибку. Все равно 12 в основе!!!
    
    lair
    16.10.2019 14:27
    #20763900
    Смотрите, мы получили число 0,170.
    Откуда вы его получили, и почему это число для нас важно?
    
    Поэтому следующее подходящее — 24. При этом ошибка уже 0,08
    Этого быть не может, потому что при дроблении ступеней пополам ошибка увеличиваться не может — старые ступени остались на своих местах.
    
    nihole Автор
    16.10.2019 14:36
    #20763940
    >Откуда вы его получили, и почему это число для нас важно?
    Кажется я начинаю понимать природу ваших вопросов :)
    Вы прочитали статью?
    
    lair
    16.10.2019 15:06
    #20764136
    Да. Более того, выше по треду я привожу вычисления из нее же.
    
    nihole Автор
    16.10.2019 13:56
    #20763698
    -1
    Ну и в случае 41, n = 7 — нечетное, значит вы прошли мимо квинты и кварты, они не попали в ваш звукоряд. Но т.к. градация очень плотная, то вы наверно это даже не почувтсвуете.
    
    lair
    16.10.2019 14:00
    #20763724
    Ну и в случае 41, n — нечетноя, значит вы прошли мимо квинты и кварты, они не попали в ваш звукоряд
    Это неправда:
    
    perfect fourth: 17 steps, 497.56 cents
    perfect fifth: 24 steps, 702.44 cents
    Ошибка по сравнению с чистыми интервалами — 0.48 цента, по сравнению с 1.96 цента в предлагаемой вами.
    
    nihole Автор
    16.10.2019 14:29
    #20763908
    -1
    конечно, потому что это 41 (а не 12) звуков. Я же написал, что ваша градуированность уже настолько плотная что вы это не услышите. Но математически вы перепрыгнули через квинту и кварту
    
    lair
    16.10.2019 14:30
    #20763912
    Что такое "математически перепрыгнул"? Дайте формальное определение этого понятия.
    
    nihole Автор
    16.10.2019 14:46
    #20763982
    -1
    ОК. Квинта это 7/12 изменения частоты в логарифмической шкале
    Вы можете представить эту частоту как
    7/12 = 14/24 = 21/36 = 7 * i/ 6 *2* i
    но вы не сможете ее представить как
    x/6* (2i + 1) где x и i целые числа
    То есть каждый раз когда вы берете деление 6* (2i + 1) вы «перепрыгиваете» через квинту
    
    Поэтому имеет смысл рассматривать только вариант 6*2*i = 12*i
    
    lair
    16.10.2019 15:07
    #20764142
    Квинта это 7/12 изменения частоты в логарифмической шкале
    Это почему? Квинта — это отношение частот (линейное) 3/2. Как вы из этого получаете ваше число?
    
    nihole Автор
    16.10.2019 15:14
    #20764200
    -1
    2 в степени 7/12 лишь на 0,1 процента (одна тысячная) отличается от 3/2
    
    lair
    16.10.2019 15:20
    #20764248
    И что? Из этого никак не вытекает, что это лучшее приближение. Поэтому использовать "7/12 в логарифмической шкале" для какого-то дальнейшнего обоснования — нельзя. Надо использовать именно 3/2.
    
    PS 2 в степени 7/12 отличается от 3/2 на 1.692923e-03. 2 в степени 24/41 отличается от 3/2 на 4.194331e-04.
    
    nihole Автор
    16.10.2019 15:24
    #20764266
    это был ответ на вопрос почему я в логарифмической шкале квинту считаю за 7/12
    То есть вам теперь понятно, почему при нечетных степенях при 6: 6,18,30,41(с учетом нарастющей ошибки) вы будете «перепрыгивать» через квинту и кварту?
    
    lair
    16.10.2019 15:28
    #20764284
    это был ответ на вопрос почему я в логарифмической шкале квинту считаю за 7/12
    … потому что вам так удобно? Никакого другого варианта я не вижу.
    
    У вас есть квинта, которая 3/2. Все надо сравнивать с ней. Это даже в вашем собственном условии написано: "соотношение частот между до и соль должно [...] равняться 3/2."
    
    То есть вам теперь понятно, почему при нечетных степенях при 6:
    А меня не интересуют "степени при 6". Меня интересует деление октавы на равные отрезки, и я уже несколько раз продемонстрировал, что есть деления, при которых ошибка уменьшается по сравнению с вашей.
    
    fesst
    16.10.2019 19:27
    #20765632
    +1
    У Вас ошибка в рассуждениях, потому что при переходе от чистой квинты к логарифмической, Вы подменяете квинту, а приравнивая 2^(7/12) к 3/2. lair прав, в том, что 2^(24/41) будет ещё больше похоже на чистую квинту, поскольку модуль разницы с 3/2 в случае 24/41 лучше.
    
    Такая подмена лишает Ваши рассуждения математичности.
    
    nihole Автор
    16.10.2019 19:30
    #20765648
    Ну, конечно, ведь вы разбили на 41 интервал.
    Так например, если сделать деление не на 41 а на 1000, то у 10 звуков рядом с квинтой точность будет лучше чем в моем случае :)
    
    nihole Автор
    16.10.2019 20:39
    #20765964
    Кстати да, действительно звуковой ряд из 41 звуков хорошо попадает и в квинту и в кварту. Проверил. Признаю.
    Все же вот эта приблизительность при таких больших числах (и соответвтенно более высокими требованиями к точности) играет роль.
    
    Но это не отменяет написанного в статье :). Конечно, когда мы используем большое количество звуков в нашем строе, мы уже не можем рассуждать приблизительно и оценочно и должны точно считать.
    
    lair
    16.10.2019 21:09
    #20766082
    Но это не отменяет написанного в статье
    … за тем небольшим исключением, что число 12 — не единственное (и даже не лучшее), удовлетворяющее вашим условиям.
    
    nihole Автор
    16.10.2019 21:19
    #20766122
    Ну, это как минимум наименьшее.
    
    lair
    16.10.2019 22:07
    #20766260
    Тоже неправда. Наименьшее — три.
    
    nihole Автор
    16.10.2019 22:12
    #20766286
    Поясните
    
    lair
    16.10.2019 22:17
    #20766304
    При делении октавы на три (равных) части получается два интервала, больший из которых имеет соотношение приблизительно 3/2, а меньший, его обращение — приблизительно 4/3.
    
    nihole Автор
    16.10.2019 22:32
    #20766372
    хм… а почему тогда не 2?
    Понимаете в чем штука, вот когда вы видите число 0,170 и вам нужно его умножить на целое число и получить тоже целое число, то вот как-то видно что лучшее наименьшее число — это 6. Но вот вы говорите 3. Но тогда, без всяких критериев и 2 также хорошо как и три. Ну бог с ними с квинтами и квартами — вот будет один интервал, он и квинта и кварта.
    
    lair
    16.10.2019 22:34
    #20766380
    Потому что ни то, ни другое деления не дают двух различных интервалов.
    
    nihole Автор
    16.10.2019 22:51
    #20766438
    ну а зачем вам различные, если при делении на 3 интервала вас не смущает разница с квинтой и квартой на величину порядка 100 центов
    
    lair
    16.10.2019 23:05
    #20766478
    Затем, что в условии задачи два разных интервала.
    
    lair
    16.10.2019 23:06
    #20766480
    Понимаете в чем штука, вот когда вы видите число 0,170
    … я вижу взятое с потолка число.
    
    вот как-то видно что лучшее наименьшее число — это 6.
    … а недавно было 12. Хм.
    
    nihole Автор
    16.10.2019 23:14
    #20766508
    в статье показано откуда оно берется
    где на ваш взгляд ошибка?
    
    lair
    16.10.2019 23:15
    #20766512
    В округлении, очевидно.
    
    nihole Автор
    16.10.2019 23:20
    #20766534
    ок
    вот у нас есть число 12 с погрешнсотью в 2 цента и число 41 с лучшей погрешностью
    
    вы выбираете 41?
    
    lair
    16.10.2019 23:24
    #20766552
    Я-то вообще не выбираю равномерный строй, я его не хочу.
    
    Но дошло до "какой вы выбираете", о какой "математической необходимости" идет речь?
    
    nihole Автор
    16.10.2019 23:36
    #20766600
    вот. Мы просто спорим не о том. Вы спорите о том насколько хорош этот строй. Я же предположив, что это необходимая реальность для современной музыки показал что в этом случае
    минимаельный звукоряд должен состоять из 12 звуков.
    Но, да, я так же думаю что это и достаточный звукоряд (но это утверждение не является основным).
    
    При этом под современной музыкой я считаю не музыку родившейся в последние десять — двадцать (ну может чуть больше) лет, а в последние 200 лет.
    
    В конце-концов для европейсокй музыки, которая насчитывает тысячилетия период в 200 лет, как мне кажется, более адекватно характеризует понятие «соверменность» чем 10 — 20 лет.
    
    lair
    16.10.2019 23:42
    #20766638
    показал что в этом случае минимаельный звукоряд должен состоять из 12 звуков.
    Нет, не показали. Вы всего лишь показали, что звукоряд из 12 звуков удовлетворяет выставленным вами условиям.
    
    При этом под современной музыкой я считаю не музыку родившейся в последние десять — двадцать (ну может чуть больше) лет, а в последние 200 лет.
    И вас совершенно не смущает, что европейская музыка за 200 лет изменилась совершенно радикальным образом?
    
    В конце-концов для европейсокй музыки, которая насчитывает тысячилетия
    Сколько, простите?
    
    период в 200 лет, как мне кажется, более адекватно характеризует понятие «соверменность» чем 10 — 20 лет.
    Вам кажется. Это еще один пример того, как вы выбираете понятия тем образом, которым вам хочется, без какого-либо объективного критерия для этого.
    
    nihole Автор
    16.10.2019 23:48
    #20766672
    -2
    Согласитесь, что нет смысла продолжать :)
    Мне казалось, что в принципе математика штука довольно объективная, но если вы просто говорите, что это все фигня, то спорить смысла нет. Мне кажется вам просто не нравится вывод.
    
    lair
    16.10.2019 23:55
    #20766696
    Математика-то штука объективная, но вы-то выбираете свои критерии произвольным образом, и в этот момент места для объективности не остается.
    
    Назовите мне хотя бы один объективный критерий, согласно которому современная музыка — это последние двести лет?
    
    (я даже не буду спрашивать, при чем тут тогда Бах и Бетховен)
    
    nihole Автор
    17.10.2019 00:02
    #20766716
    -1
    Давайте на этом остановимся.
    В любом случае спасибо за 41 — это было интересно
    
    lair
    17.10.2019 00:27
    #20766770
    … а вы говорите — объективность.
    
    nihole Автор
    17.10.2019 00:57
    #20766854
    -1
    так нет смысла спорить, когда перед вами лежит доказательство, а вы говорите: «Для меня очевидно, что нет никакого смысла умножать 0.170 на три. „
    
    Что тут еще можно сказать — уже все сказано в статье.
    Или по существу, или — спокойно ночи.
    
    Просто интересно — у вас какое образование?
    
    lair
    17.10.2019 01:04
    #20766874
    так нет смысла спорить, когда перед вами лежит доказательство
    Перед вами — тоже, но вы его игнорируете.
    
    Вы, я повторюсь, даже в математических терминах задачу не формализовали до сих пор, о каком доказательстве идет речь?
    
    Просто интересно — у вас какое образование?
    Вы не поверите: высшее, история и теория музыки.
    
    nihole Автор
    17.10.2019 01:06
    #20766878
    -2
    да нет, в это как раз я верю
    и понятно почему вы игнорируете математическое доказательство
    
    lair
    17.10.2019 01:06
    #20766882
    Повторюсь еще раз: у вас нет строгой формулировки задачи в математических терминах, о каком математическом доказательстве идет речь?
    
    nihole Автор
    17.10.2019 01:09
    #20766884
    математика оперирует в том числе и с приблизительными величинами
    задача сформулирована достаточно ясно, чтобы получить ответ
    
    lair
    17.10.2019 01:10
    #20766892
    задача сформулирована достаточно ясно, чтобы получить ответ
    Покажите (полную и достаточную) формулировку в математических терминах.
    
    nihole Автор
    17.10.2019 01:11
    #20766896
    у меня физико-математическое образование
    поверьте мне на слово
    
    lair
    17.10.2019 01:12
    #20766898
    Нет, не поверю (вы же не верите мне на слово, когда я вам говорю, что ваши выкладки о современной музыке неверны). Покажите формулировку. "Нужно найти такое N, чтобы...".
    
    nihole Автор
    17.10.2019 01:15
    #20766904
    читайте статью
    и простите, я пас
    
    lair
    17.10.2019 01:17
    #20766910
    А в статье такой формулировки нет (если бы она была, вы бы могли ее просто скопировать, это не так сложно).
    
    О чем, собственно, и речь.
    
    А когда задачу за вас сформулировали, вы проигнорировали решение, потому что оно не сошлось с вашим.
    
    nihole Автор
    17.10.2019 01:21
    #20766918
    -1
    Ей богу, разговор слепого с глухим
    Спокойной ночи
    
    lair
    17.10.2019 01:23
    #20766924
    Я подозреваю, что намного проще уходить от ответа на прямой неудобный вопрос, нежели признать, что ответа просто нет.
    
    И это, на самом деле, очень грустно.
    
    nihole Автор
    17.10.2019 01:30
    #20766932
    Грустно. Но суть в том что в статье все есть.
    Конечно, это не статья по математике и я пытался быть краток, поэтому не все детали оговорены и кое-где может быть были (и есть) неточные формулировки и может быть даже слишком агрессивные выводы, но если бы вы действительно поняли математическую часть то 90 процентов этой беседы не было бы.
    Вы бы поняли, что 12 — это не случайное число а предопределенное если хотите число и что причина этого в том, что логарифм 3 по основанию 2 c хорошей точностью равен 19/12
    
    Знаете, у меня есть идея написать еще одну статью. Я думаю после нее будет все понятней
    
    Давайте отложим этот диалог до следующего раза
    
    lair
    17.10.2019 01:40
    #20766946
    Но суть в том что в статье все есть.
    В статье нет самого важного: доказательства того, что число 12 чем-то уникально в рамках поставленной вами задачи.
    
    если бы вы действительно поняли математическую часть то 90 процентов этой беседы не было бы.
    Проблема в том, что я понимаю математическую часть, иначе бы я не смог написать, где конкретно там ошибка, как я сделал выше. И, что занятно, ни на одну ошибку в моих выкладках никто не указал.
    
    причина этого в том, что логарифм 3 по основанию 2 c хорошей точностью равен 19/12
    "С хорошей точностью" — это такая принятая математическая формулировка, да? А можете сослаться на какой-нибудь авторитетный источник, где вводится это понятие?
    
    А что делать с тем фактом, что логарифм 3 по основанию два с большей (приблизительно в четыре раза) точностью равен 65/41, и с еще большей (более чем в двадцать раз) — 84/53?
    
    nihole Автор
    17.10.2019 01:47
    #20766950
    ну точность такая что квинта у вас при этом воспроизводится с точностью до 2х центов
    вам это достаточно?
    
    и я вас уже спрашивал, вот вы имеете
    12 (с точностью 2 цента), 41 и 53 (с гораздо лушей точночтью) — что вы выбираете
    
    ну не хотел я расписывать и разжевывать все
    мне кажется и так все очевидно и каждый может додумать и досчитать сам
    
    lair
    17.10.2019 01:48
    #20766954
    ну точность такая что квинта у вас при этом воспроизводится с точностью до 2х центов
    Что из этого является математическим термином?
    
    что вы выбираете
    Какая разница, что я выбираю, если мы говорим о формальной математической задаче? Какое решение удовлетворяет этой задаче?
    
    nihole Автор
    17.10.2019 10:07
    #20767902
    Ну послушайте, мне действительно сложно с вами общаться — мы из разных миров. Вы просто говорите какие-то вещи, которые в принципе очевидны и я не вижу смысла их даже обсуждать. Они подразумеваются.
    
    Понятно, что чем больше знаменатель вы берете тем лучше будет ваше приближение к иррациональному числу. Вы могли бы вообще не заморачиваться рассчетами, а тупа брать 10, 100, 1000, 10000 и с каждым разом ваше приближение будет все ближе и ближе.
    
    Так же понятно, что если у вас есть ошибка (неточность) потому что ваша формула приблизительна, то при некоторых математических операциях (например умножении) это ошибка будет увеличиваться, но я же в статье ограничился лишь малыми числами i потому что посчитал что большие i рассметривать нет смысла. Не потому, что там не будет квинт и кварт, а потому что по разным причинам такая градуированность (ИМХО конечно — я понимаю что вы с этим не согласны) не нужна.
    
    Конечно, если бы это была статья по физике и математике, то все эти вещи (какая точность требуется, какая ошибка) были бы оговорены, но это НЕ статья по математике и в принципе все эти вещи то очевидны. Это можно было бы обсудить но не с позиции прав — не прав и спокойно.
    
    Вот мы потратили столько времени, и все лишь для того чтобы я вам в энный раз сказал — 12 это наименьшее «хорошее» число. И видно это из того что 0,170 * 6i (при малых i конечно) дает число близкое к целому (но i = 1 нам не подходит)!
    
    Но ваш ответ на это (который уже тоже неоднократно встречался) в том, что вы не понимает откуда и почему я беру число 0,170, но ответ то в статье. В этом и суть математики — мне надо вот по идее ничего уже объяснять!
    
    lair
    17.10.2019 11:37
    #20768366
    Вы просто говорите какие-то вещи, которые в принципе очевидны и я не вижу смысла их даже обсуждать.
    Знаете, вы тоже говорите какие-то вещи, которые в принципе очевидны… очевидно неправильны, в смысле. И это действительно нет особого смысла обсуждать, но вы продолжаете использовать эти очевидно неправильные суждения для аргументации в пользу своей точки зрения.
    
    Понятно, что чем больше знаменатель вы берете тем лучше будет ваше приближение к иррациональному числу.
    Почему-то если взять тринадцать ступеней вместо двенадцати, ошибка увеличивается. Хотя знаменатель больше.
    
    Так же понятно, что если у вас есть ошибка (неточность) потому что ваша формула приблизительна, то при некоторых математических операциях (например умножении) это ошибка будет увеличиваться,
    … и какое это имеет отношение к дискусии? Покажите мне хотя бы один пример в ваших или моих расчетах, где происходит накопление ошибки.
    
    но я же в статье ограничился лишь малыми числами i
    … хотя увеличение i — если вы, конечно, говорите об i в 6i — само по себе не ведет к увеличению ошибки. Так при чем тут это?
    
    это НЕ статья по математике
    А по чему эта статья? По теории музыки? Тоже нет.
    
    в принципе все эти вещи то очевидны
    Как раз наоборот. Если это статья не по математике, вам надо оговаривать все математические допущения, которые вы делаете, именно потому, что вы находитесь за пределами стандартного контекста.
    
    12 это наименьшее «хорошее» число
    Что такое "хорошее" число? Не субъективно "мне нравится", а объективно?
    
    И видно это из того что 0,170 * 6i (при малых i конечно) дает число близкое к целому
    А при больших — не дает? Да нет, дает. Я помножил на 300 (ну так, от балды), и получил целое число.
    
    но i = 1 нам не подходит
    Почему? Оно формально удовлетворяет условиям задачи.
    
    вы не понимает откуда и почему я беру число 0,170
    Я понимаю, откуда вы берете это число. Я не понимаю, зачем вы держитесь за него держитесь, хотя это очевидно приближенное значение, когда вы могли бы оперировать исходным log2(9/8) (или, что характерно, log2(3/2), потому что вам достаточно минимизировать ошибку на чистой квинте), и иметь формальную точность в ваших вычислениях, а не "хорошие числа".
    
    В этом и суть математики — мне надо вот по идее ничего уже объяснять!
    Вы уж определитесь, это статья по математике или нет. Потому что если не по математике, то вам придется объяснять каждый математический шаг.
    
    nihole Автор
    17.10.2019 12:29
    #20768864
    -1
    Ну я же говорю… Вы только подтвердили мое высказывание.
    Отвечу только вот на это потому что все остальное — мыло да мочало начинай сначала
    
    >Почему-то если взять тринадцать ступеней вместо двенадцати, ошибка увеличивается. Хотя знаменатель больше.
    
    Знаете, понимая уже вашу дотошность я знал что вы это напишете :).
    Конечно, мое утверждение было не совсем точным, потому что ну вот я не на экзамене и не на математическом форуме и мы говорим о вещах очевидных, так что можно просто намекнуть и не приводить точные формулировки. Но вам не понятно. Там же даже пример приведен — 100, 1000, 10000… Ну ок.
    Мы должны говорить о степенях конечно. Вот тот пример был со степенью 10
    Но давайте возьмем степень 2.
    16, 32, 64, 128, 256,… (или степень любого другого числа)
    вот беря их в качестве знаменателя вы будете все ближе приближаться к вашему иррациональному числу. И здесь все будет линейно. 32 будет прибижать лучше чем 16, 64 — чем 32… Поэтому просто беря числа все больше и больше вы будете находить числа, которые все ближе и ближе к вашему значению. Поэтому взяв например этот ряд (16, 32, 64… ) для 128 мы уже получаем для 75 ступени около одного цента отличие отк квинты и теперь для всех остальных чисел в (256, 512 ...) результат будет все лучше и лучше.
    
    Поэтому это общая тенденция улучшения при увеличении знаменателя. Она не монотонна.
    
    lair
    17.10.2019 12:37
    #20768938
    все остальное — мыло да мочало начинай сначала
    Вот, например, вопрос, "по чему" эта статья, если не по математике.
    
    мы говорим о вещах очевидных
    Кому очевидных?
    
    Поэтому просто беря числа все больше и больше вы будете находить числа, которые все ближе и ближе к вашему значению.
    Казалось бы, из этого очевидно, что 12 — не уникальное и не лучшее число. Так почему же вы продолжаете пытаться это доказать?
    
    nihole Автор
    17.10.2019 12:57
    #20769092
    -1
    Почитайте статьи по математике в научных журналах — увидите разницу. Разица во-первых в сложности (это школьная математика), а во-вторых, в строгости суждения (это научно-популярный стиль изложения — очень лайт). И если бы я написал ее в стиле академической научной статьи вы бы первый уснули бы на первом абзаце.
    
    На второе уже нет смысла отвечать — отвечал много раз.
    
    lair
    17.10.2019 13:43
    #20769410
    Почитайте статьи по математике в научных журналах — увидите разницу.
    Да я вижу разницу. Я спрашиваю, по чему эта статья, если не по математике.
    
    И если бы я написал ее в стиле академической научной статьи вы бы первый уснули бы на первом абзаце.
    Я читал академические научные статьи, спасибо.
    
    На второе уже нет смысла отвечать — отвечал много раз.
    Нет, вы ни разу не ответили, почему вы считаете, что число 12 уникально. Ну то есть нет, я не прав. Почему вы считаете — ответили. Но почему вы считаете это математически доказанным фактом?
    
    nihole Автор
    17.10.2019 14:50
    #20769880
    Это есть в статье, и я разъяснял вам это уже в коммнтариях.
    Очень сложно объяснить что-то человеку, который не просто не пытается понять, но пытается НЕ понять.
    
    lair
    17.10.2019 14:53
    #20769898
    Это есть в статье
    Выкладки в статье недостаточны, и это, казалось бы, уже неоднократно показано.
    
    Да блин (извините), уникальность опровергается одним контрпримером, вам их привели не меньше трех, ну о чем тут можно говорить?
    
    nihole Автор
    17.10.2019 15:23
    #20770132
    -1
    Давайте, последняя попытка, которую вы опять используете, чтобы меня минусануть, к чему то придраться или просто не понять, но все же если мне все еще кажется что человек хочет понять что-то, то я пытаюсь объянить.
    
    Я не очень понимаю что вы опровергаете?
    
    То что вы привели числа много большие чем 12, которые так же решают поставленную задачу (и даже лучше)?
    
    И что вы этим опровергли? Я же говорю вот числа 256, 512, 1024… (до бесконечности) все будут удовлетворять требованиям задачи и даже лучше чем 12. И что?
    
    Я же нигде не сказал что 12 — это единственное число. Более того, я же говорил что 24 — тоже хорошее число.
    
    12 — это первое удовлетворительное число. Следующее 24. И ни 3 ни 4 ни… 11 не дают тот же результат. И потом от 13 до 23 — тоже не то.
    
    В этом смылсе 12 уникально!
    
    Вы можете конечно построить звукоряд и на 41 звуке ( а так же и на бесконечном количестве комбинаций с большим количеством звуков в звукоряде), но ИМХО это не имеет большого смысла (вот здесь конечно можно спорить, но статья то не об этом)
    
    Еще раз. Посыл этой статьи в том, что 12 — не случайное число. Ну вот не могло быть 11 или 10 или как вы предлагали 3. 19 — тоже не очень хорошее число — квинта 7 центов мимо (во всяком случае в рамках сформулированных требований)
    
    lair
    17.10.2019 15:37
    #20770228
    Я не очень понимаю что вы опровергаете?
    То, что 12 — уникальное число, подходящее под ваши условия.
    
    И что?
    И то, что 12 — не уникально.
    
    Я же нигде не сказал что 12 — это единственное число.
    Вот прямо двумя абзацами ниже в этом же комменте.
    Или вот вам цитата: "остается только одно число: 12".
    
    В этом смылсе 12 уникально!
    Нет, не уникально. Первое "удовлетворительное число" — 3.
    
    Но вообще, формулировка "первое число (из бесконечного множества), удовлетворяющее требованиям — уникально" меня потрясает своей бессмысленностью.
    
    19 — тоже не очень хорошее число — квинта 7 центов мимо (во всяком случае в рамках сформулированных требований)
    У вас нет такого сформулированного требования.
    
    nihole Автор
    17.10.2019 15:52
    #20770334
    -1
    Ну, т.к. формулы, судя по всему, не ваш конек привожу табличку (сделал специально для вас)
    
    Первый столбец — число звуков в вашем звукоряде
    Второй — разница с чистой квинтой в центах
    
    3 98
    4 100
    5 18
    6 98
    7 16
    8 48
    9 35
    10 18
    11 47
    12 2
    13 36
    14 16
    15 18
    16 27
    17 4
    18 31
    19 7
    20 18
    21 16
    22 7
    23 28
    24 2
    25 18
    26 10
    27 9
    28 16
    29 1,5
    
    Минимумы (ниже 2 центов): 12, 24, 29
    17 — тоже неплохо, но все же в 2 раза хуже
    
    Нет?
    
    lair
    17.10.2019 16:10
    #20770436
    Нет.
    
    Минимум — 29. И про 29 EDO я вам написал больше суток назад.
    
    nihole Автор
    17.10.2019 16:15
    #20770460
    ну… я пытался
    
    nihole Автор
    17.10.2019 16:16
    #20770468
    -1
    Минимум в бесконечности, например 2 в бесконечной степени будет минимумом и это будет ровный 0 центов, да хотя любое бесконечное число даст вам настоящий минимум (0 смещение, причем не только от квинты но и от любых чистых интервалов)
    
    Поэтому не очень понятно, почему вы считаете 29 минимумом
    
    lair
    17.10.2019 16:19
    #20770480
    Казалось бы, очевидно, что минимум из представленной вами таблицы (почему вы решили выбрать именно такую таблицу — это к вам вопрос, не ко мне).
    
    nihole Автор
    17.10.2019 16:22
    #20770496
    -1
    почитайте пожалуйста на досуге, что такое минимумы и максимумы функций
    я же говорю мы с вами из разных миров и говорим на разных языках
    
    lair
    17.10.2019 16:23
    #20770508
    -1
    почитайте пожалуйста на досуге, что такое минимумы и максимумы функций
    Спасибо, я в курсе. Какую таблицу дали, какой вопрос поставили, такой ответ и получили.
    
    nihole Автор
    17.10.2019 16:30
    #20770542
    -1
    Нет, судя по всему вы не в курсе
    
    lair
    17.10.2019 17:15
    #20770814
    Ну, если вы мне покажете определение, согласно которому 1.5 цента не является минимальным значением в этой таблице, у меня будет возможность исправить эти пробелы в моем образовании.
    
    haryaalcar
    18.10.2019 12:09
    #20774596
    Вы считаете, что полцента оправдывает такую ужасающую потерю эргономики?
    
    lair
    18.10.2019 12:12
    #20774616
    Понимаете ли, в чем дело. "Я считаю, что [не] оправдывает" — это субъективное суждение. Я могу так считать, кто-то другой может считать иначе; кому-то много 12 клавиш, у кого-то струнный (безладовый) инструмент, для которого это все вообще мелочи. Это все субъективно.
    
    А автор утверждает, что число 12 обусловлено объективными причинами.
    
    lair
    17.10.2019 16:22
    #20770500
    На всякий случай:
    
    Normal adults are able to recognize pitch differences of as small as 25 cents very reliably.
    [...]
    vibrato span typically ranged between ±34 cents and ±123 cents with a mean of ±71 cents
    
    nihole Автор
    17.10.2019 16:28
    #20770534
    -1
    ну да, тоже на всякий случай
    «К изменениям высоты, громкости и тембра С. м. наиболее чувствителен в среднем регистре — примерно от 500 до 3000-4000 герц, здесь музыканты различают изменения высоты в 5-6 центов»
    и вы сами жаловались что все криво звучит, а тут вдруг 25 центов
    
    Ладно, надо заканчивать этот троллинг с вашй стороны. Вы просто очень не хотите… или получаете от этого удовольствие
    Всего хорошого
    
    lair
    17.10.2019 17:16
    #20770816
    вы сами жаловались что все криво звучит, а тут вдруг 25 центов
    Ну так одно другому не противоречит.
    
    Druu
    18.10.2019 12:52
    #20774826
    Normal adults are able to recognize pitch differences of as small as 25 cents very reliably.
    Тут вот, конечно, надо уточнять, как идет распознавание. Если просто в изолированном виде дать послушать ноту а потом следом за ней другую — будет распознавание точнее. Если дать интервал — будет еще точнее, т.к. биения, и там вообще до единиц центов их можно услышать. Если идет какая-то мелодия — важна не погрешность ноты, а погрешность соответствующего интервала. И то, какой интервал. И то, какой мелодический контекст.
    
    ЗЫ: вибрато на 100 центов — это уже не вибрато а быстрые слайды :))
    
    lair
    18.10.2019 13:30
    #20775054
    Тут вот, конечно, надо уточнять, как идет распознавание.
    Да там, собственно, абзацем раньше много таких оговорок, и про гармонию, и про то, что тональный контекст повышает точность. Но в первую очередь пишут, что разброс адский.
    
    вибрато на 100 центов — это уже не вибрато а быстрые слайды
    Вокалисты, страшные люди.
    
    lair
    17.10.2019 01:50
    #20766960
    … а 16/10 всего лишь в десять раз менее точно приближает нужный вам логарифм. А 46/29 — наоборот, более точно.
    
    nihole Автор
    17.10.2019 01:10
    #20766894
    И почему вы минусуете каждый мой ответ — это не способствует конструктивному диалогу
    
    Druu
    17.10.2019 09:04
    #20767584
    +1
    Я же предположив, что это необходимая реальность для современной музыки показал что в этом случае
    минимаельный звукоряд должен состоять из 12 звуков.
    Смотрите, 12 звуков в октаве было до равномерной темперации вообще, по-этому вы не можете обосновывать 12 звуков при помощи темперации, это будет просто неверно заведомо :)
    
    12 получается от того, что если вы будете поочередно отстраивать квинты друг за другом и смотреть, на сколько эта последовательность квинт отличается от целого числа октав, то вы получите через 12 квинт второй локальный минимум (первый получается через 5 квинт, это будет си, и система, замыкаемая через этот минимум, будет пентатоникой). При этом дальнейшие минимумы будут наоборот удаляться достаточно долго. По-этому 12. А уже потом взяли погрешность этого минимума и размазали по всем квинтам.
    
    nihole Автор
    17.10.2019 10:14
    #20767932
    >Смотрите, 12 звуков в октаве было до равномерной темперации вообще, по-этому вы не можете обосновывать 12 звуков при помощи темперации, это будет просто неверно заведомо :)
    
    Это хорошее замечание. У меня есть что сказать на это :)
    Но это я приберег для следующей статьи
    
    nihole Автор
    16.10.2019 23:18
    #20766528
    я же объяснил в статье
    все же мне кажется вы не поняли что там написано
    уровнение которое там приведено (и откуда берется 6*i) исходит из того что между квиной и квартой должно быть целое колическтво интервалов, но это не значит, что когда вы откладываете эти интервалы от тоники квинта и кварта туда попадают
    и вот для 6 — не попадают
    поэтому 6 — не подходит (хотя и удовлетворяет условию)
    а вот следующее число 12 — подходит
    
    я это вам уже и отдельно пытался объяснить
    
    вот вы столько пишете, но прочитаейте внимательно статью
    
    мне кажется дальше, пока не будет конструктивной критики нет смыслка продолжать
    
    lair
    16.10.2019 23:27
    #20766560
    уровнение которое там приведено (и откуда берется 6*i) исходит из того что между квиной и квартой должно быть целое колическтво интервалов, но это не значит, что когда вы откладываете эти интервалы от тоники квинта и кварта туда попадают
    Это, прямо скажем, невозможно. И поэтому шесть — подходит (просто дает ту же погрешность на квинте, что и 3).
    
    прочитаейте внимательно статью
    Я как раз прочитал статью внимательно. И в ней есть сильно больше одной методической ошибки, которые вы упорно продлжаете игнорировать.
    
    nihole Автор
    16.10.2019 23:38
    #20766612
    Не знаю что ответить. Если для все не очевидно, что 0,170 * 6 ближе к целому числу чем 0,170 * 3, то спор не имеет смысла.
    
    lair
    16.10.2019 23:43
    #20766648
    Для меня очевидно, что нет никакого смысла умножать 0.170 на три. Более того, нет никакого смысла даже вводить 0.170, надо оперировать исходными числами.
    
    А вы зацепились за это 0.170, и пытаетесь от него все построить, хотя оно не имеет значения.

Refridgerator
15.10.2019 20:18
#20759626
+7
Стало быть, о 19-и, 24-x, 31-x и 53-х ступенчатой темперации вы ничего не слышали?
1. nihole Автор
  15.10.2019 21:42
  #20760104
  Смотрите замечание выше!
1. nihole Автор
  15.10.2019 22:17
  #20760276
  В статье же все показано с точки зрения математики.
  Ну вот смотрите. 24 ступенчатая темперация — ок. В статье это число тоже получается.
  Но если вы уножите 0,17 на 19 или 31 но вы не получите целого числа
  0,17 x 19 = 3,23
  0,17 x 31 = 5,27
  
  При умножении на 53 имеем что-то близкое
  
  0,17 x 53 = 9,01
  
  Но это потому что это число близко к 54 = 6 x 9
  Но девятка — нечентное число.
  
  Все это значит, что если вы применяете принцип инвариантности, то вы теряете в вашем звуковом ряде квинты и/или кварты
  Или вы сохраняете квинты и кварты, но теряете инвариантность.
  
  Я ничего не имею против, но я писал про другую музыку
  1. math_coder
    15.10.2019 22:24
    #20760314
    +2
    Вы писали про современную музыку.
    
    Интересно, в каком строе и в какой тональности чаще всего играют "4:33"?

maxkomp
15.10.2019 20:19
#20759634
+4
Небольшое дополнение.
Рассказ о равномерно темперированном музыкальном строе был бы неполным без упоминания о человеке, который, собственно, все это придумал. То есть о немецком математике и музыканте Андреасе Веркмейстере.

Подробности — https://ru.wikipedia.org/wiki/Веркмейстер,_Андреас
Еще много интересного про теоретическую основу музыки (причем «на пальцах», то есть без заумных математических формул) можно почитать в книжке Спартака Суреновича Газаряна, «В мире музыкальных инструментов». (Ее в гугле поищите).
1. lair
  15.10.2019 20:50
  #20759794
  +2
  Рассказ о равномерно темперированном музыкальном строе был бы неполным без упоминания о человеке, который, собственно, все это придумал. То есть о немецком математике и музыканте Андреасе Веркмейстере.
  Прямо по вашей же ссылке написано, что Веркмейстер равномерную темперацию не изобретал (и, прямо скажем, скептически к ней относился).

sith
15.10.2019 20:27
#20759676
+3
Вот нравилось нашим предкам число 12, у них везде 12

12 не просто так понравилось и получило очень широкое распространение (измерение времени, длин, весов, объёмов, денежных единиц и так далее). Оно делится без остатка на 2,3,4,6 в отличии от, например, 10, которое делится только на 2 и 5.
1. nihole Автор
  15.10.2019 22:05
  #20760224
  почему тогда не 60?
  Оно еще и на 5 делится
  1. MechanicZelenyy
    15.10.2019 22:11
    #20760242
    60 секунд, 60 минут, 360 градусов.
    
    nihole Автор
    15.10.2019 22:18
    #20760280
    ну не спорю). Но мы же про музыку
    
    tabmoo
    17.10.2019 10:27
    #20767990
    60 использовалось в цивилизациях Междуречья, оттуда все эти минуты, секунды, градусы. Более того, в один период там даже использовался контроль работников 60 раз в сутки (рабочий день)! Это вам не скрины рабочего стола раз в час!
  1. sith
    15.10.2019 22:26
    #20760332
    Кроме 12 есть 24, 36 и 60. Все они делятся на 12 (значит и на 2,3,4,6 тоже).
    
    Lennonenko
    16.10.2019 00:03
    #20760810
    +1
    12 считается на пальцах же, а 60 — нет
    
    Wizard_of_light
    16.10.2019 10:36
    #20762408
    12 фаланг одной руки + 5 пальцев второй, большой палец первой руки используется как указатель фаланги. А вообще некоторые на пальцах считали до сотни миллионов.
    
    Lennonenko
    16.10.2019 12:28
    #20763134
    интересная статья, спасибо
  1. mistergrim
    16.10.2019 06:49
    #20761410
    ru.wikipedia.org/wiki/Шестидесятеричная_система_счисления
1. iShrimp
  16.10.2019 20:33
  #20765934
  Из всех надмножеств 12-ступенного строя, пожалуй, лучший — 72EDO. Под него был изготовлен легендарный советский синтезатор АНС. В нём удобно запоминать и играть мелодии, в этот строй хорошо укладываются многие натуральные интервалы:
  квинта (3/2) в 72edo — 42 ступени — равна квинте 12edo (6*7=42);
  большая терция (5/4) — 23 ступени — на 1/6 полутона меньше аналогичного интервала в 12edo;
  малая терция (6/5) — 19 ступеней — на 1/6 полутона больше аналогичного интервала в 12edo;
  натуральная септима (7/4) — 58 ступеней — на 1/3 полутона меньше малой септимы в 12edo;
  полуувеличенная кварта (11/8) — 33 ступени — равна 4.5 полутона в 12edo;
  существуют большой тон (9/8) — 12 ступеней и малый тон (10/9) — 11 ступеней;
  при движении по терциям/секстам добавляется или отнимается одна ступенька (1/72 октавы), а по квинтам и квартам — нет.

daiver19
15.10.2019 20:31
#20759696
+7
Число, лежащее в основе современной музыки

Современной западной музыки.
1. nihole Автор
  15.10.2019 21:43
  #20760112
  Да, пожалуй. Но мы же западные люди. Я слушаю только западную (или порождение западной)
  1. lair
    15.10.2019 21:44
    #20760122
    +8
    Вы слушаете музыку, которая построена на 12 нотах, и пытаетесь найти число, которое лежит в ее основе. Занятное изыскание.
    
    nihole Автор
    15.10.2019 22:51
    #20760470
    +1
    Я не понял этого посыла.
    Вы можете указать, где вы видите ошибку в рассуждении?
    
    lair
    15.10.2019 23:00
    #20760540
    +3
    Ошибка не в рассуждении, ошибка в постановке задачи. Вы взяли некое очень узкое подмножество музыки, про которое известно, что оно построено на системе из двенадцати нот, а теперь пытаетесь доказать, что 12 — единственное число, удовлетворяющее этой системе, взяв два произвольных нравящихся вам требования. Неудивительно, что после приблизительных вычислений ответ сходится.
    
    nihole Автор
    15.10.2019 23:17
    #20760610
    нет не так. Я взял 2 требования и обосновал разумность каждого из них:
    1 — в вашем звукоряде должны быть тоника квинта и октава
    2 — инвариантность (наверно не музыкальный термин, но я объяснил что имею ввиду)
    и эти два дают так же и требование чтобы была кварта
    
    И получил что это может быть только для 12*i
    
    Какое из требований кажется вам неразумным?
    
    lair
    15.10.2019 23:19
    #20760622
    в вашем звукоряде должны быть тоника квинта и октава
    … а была октава, квинта и кварта...
    
    Какое из требований кажется вам неразумным?
    Оба.
    
    И получил что это может быть только для 12*i
    Неа, вы не получили этого. В полученном вами звукоряде нет чистой квинты.
    
    А, и отдельно мне кажется неразумным то, что вы так и не объяснили, о какой музыке вы говорите. Пока получается, что вы говорите о музыке, которую лично вы слушаете.
    
    nihole Автор
    16.10.2019 00:21
    #20760860
    про кварту я же описал
    если у вас есть квинта и требование инвариантности, то кварта получается автоматически — это не понятно?
    
    я получил квинту с точностью 0,1 % (одна десятая процента !!!) — вам этой точности недостаточно?
    
    например, любая фортепианная музыка, которая не предусматривает изменения строя: Бах, Бетховен, Лист, Рахманинов…
    
    Любая современная джазовая музыка — в последнее время слушаю Brad Mehldau, Monty Alexander, Muchel Petruciani, Chick Corea
    
    Мне сложнее назвать соврменную музыку к которой эти бы принципы не подошли.
    
    lair
    16.10.2019 00:37
    #20760912
    +1
    если у вас есть квинта и требование инвариантности, то кварта получается автоматически — это не понятно?
    Вот только требование инвариантности — произвольное.
    
    я получил квинту с точностью 0,1 % (одна десятая процента !!!) — вам этой точности недостаточно?
    Недостаточно. Нет определения, какая точность достаточна, а какая — нет.
    
    например, любая фортепианная музыка, которая не предусматривает изменения строя: Бах, Бетховен, Лист, Рахманинов…
    Что значит "не предусматривает изменения строя"? Бах не писал для равномерной темперации (да и для фортепиано он не писал).
    
    Ну и да. А не-фортепианная музыка? А все, что до Баха? А послевоенный двадцатый век, в частности, сонорика? А народная музыка? А смесь всего этого вместе, как у Kronos Quartet или Danish String Quartet?
    
    Кстати, а "Литургия Иоанна Златоуста" и "Всенощное Бдение" Рахманинова — они для какого строя написаны?
    
    Любая современная джазовая музыка — в последнее время слушаю Brad Mehldau, Monty Alexander, Muchel Petruciani, Chick Corea
    "Microtonal variation of intervals is standard practice in the African-American musical forms of spirituals, blues and jazz (Cook and Pople 2004, 124–26)."
    
    Мне сложнее назвать соврменную музыку к которой эти бы принципы не подошли.
    Не вставая с места — фламенко. Это в том смысле, что не надо ничего искать, не надо думать, прямо в википедии написано. Но опять же, вы не даете определения "современная" (потому что из перечисленных вами академических авторов современным не является ни один). Lachrym? Antiqu? Кроноса — это современная музыка? Саундтрек к Ghost in the Shell Кендзи Каваи — это современная музыка? "Terror in Tokyo" Йоко Канно? "Sing Me Home" Silk Road Ensemble? Музыка к Fla-co-men Израэля Гальвана и Xenos Акрама Кхана?
    
    lair
    16.10.2019 00:48
    #20760950
    я получил квинту с точностью 0,1 % (одна десятая процента !!!) — вам этой точности недостаточно?
    … а в 29 EDO и в 41 EDO погрешность (на квинте) еще ниже. Это явно показывает нам, что 12 — не уникальное число в этом отношении. И, что характерно, 29 EDO была предложена в XIV веке.
    
    adictive_max
    16.10.2019 09:16
    #20761910
    Извините, конечно, но «узкое подмножество»? Я понимаю, что если мерить в штуках, то всяких извращённых нотных систем можно наплодить хоть миллион, но давайте всё таки делать поправку на распространённость.
    
    lair
    16.10.2019 11:18
    #20762662
    Извините, конечно, но «узкое подмножество»?
    Ну да.
    
    давайте всё таки делать поправку на распространённость.
    Давайте. Вы правда думаете, что фортепианная музыка западноевропейской классико-романтической традиции — это сильно распространенная штука?
1. math_coder
  15.10.2019 22:34
  #20760380
  Да даже если ещё сильнее сузить и выкинуть современную западную академическую музыку (хотя это уже совсем нечестно), останется ещё, например, noise.
  1. lair
    15.10.2019 22:38
    #20760404
    останется ещё, например, noise.
    … или фламенко.
1. nihole Автор
  15.10.2019 23:49
  #20760746
  +1
  Да, в нескольких местах добавил слово «европейская». Спасибо!
  1. lair
    16.10.2019 00:01
    #20760802
    Фламенко — не современная европейская музыка?
    
    adictive_max
    16.10.2019 09:18
    #20761928
    То, что музыку играют сегодня, не означает что положенные в её основу принципы современны.
    
    lair
    16.10.2019 11:18
    #20762666
    Конечно.
    
    И в этот момент, собственно, возникает вопрос: так что же автор называет "современной" музыкой?
    
    bat654321
    16.10.2019 12:29
    #20763144
    +1
    То что играют сегодня не всегда является музыкой
    
    lair
    17.10.2019 11:45
    #20768430
    … мы вот выяснили, что автор считает современной музыкой то, что написано в последние 200 лет. Фламенко точно попадает.

headfire
15.10.2019 20:35
#20759722
math.ru/lib/plm/37

nehrung
15.10.2019 21:18
#20759942
С привлечением одной лишь математики, удивительно… Не зря говорят, что музыка — самое абстрактное из искусств.
Я тоже задумывался между делом, почему музыка столь прицельно бьёт по эмоциям, и полагал, что без привлечения психологии это не объяснить.

lair
15.10.2019 21:19
#20759948
+3
Заключается это требование в том, что все гармонии в любых тональностях должны звучать одинаково.
… одинаково плохо, вы хотели сказать?

Если мы говорим про современный строй, который применяется при настройке фортепиано, то это значит, что квинта, состоящая из семи полутонов, должна звучать одинаково, независимо от того, от какого звука она построена. То есть соотношение частот между до и соль должно быть таким же как и для до# — соль#, ре — ля, ре# — ля#,… и равняться 3/2.
Вы же знаете, да, что это требование невыполнимо?

Нужно сказать, что это требование инвариантности не является таким очевидным
Оно вообще не является очевидным, и более того, до сих пор не обязательно.

и данный подход был применен относительно недавно, лишь в 18 веке.
… а был ли? Назовите, пожалуйста, известные произведения XVIII века, которые доказано написаны для равномерной темперации.

Например, "Хорошо темперированный клавир" Баха появился именно благодаря новому подходу в настройке клавишных.
"Хорошо темперированный клавир", как, казалось бы, можно догадаться из названия, написан не для равномерной, а для хорошей темперации. Так что, вновь, ваше требование — произвольно.

Именно вот эта инвариантность дала возможность Баху создавать гармонические последовательности, которые просто были невозможны раньше.
Вы, конечно же, можете показать "невозможную раньше" гармоническую последовательность у Баха, и объяснить, почему она возможна только в равномерной темперации?

Но вернемся на минутку к определению вашего "требования".

Заключается это требование в том, что все гармонии в любых тональностях должны звучать одинаково.
Но что такое "тональность"? Почему вы строите требования к структуре музыкального строя исходя из какого-то дополнительного внешнего понятия (которое, будем честными, по отношению к музыкальному строю даже не вторично, а третично)?

Легко увидеть, что решением (конечно, приблизительным) является
Угу. Приблизительным. Вот и все ваше доказательство — оно приблизительно. Потому что вы сочли, что этой приближенности достаточно для целей вашего доказательства, но где аргументы?

есть единственным вариантом для нас может быть
А почему вы не рассматриваете i = 3?

Но почему не 24, 36, 48…? Причина проста — наш слух уже не различает этой градуированности.
Если бы наш слух не различал четверти тона (а это то, что получится, если поделить октаву на 24 части), не было бы никакой разницы между всеми темперациями. А она есть, даже вы ее упоминаете. Следовательно, слух различает эти градации. Следовательно, и ваш вывод об уникальности числа 12 — ошибочен.

Но, впрочем, он был ошибочен еще тогда, когда вы решили, что равномерная темперация обязательна.
1. epishman
  15.10.2019 21:30
  #20760014
  Равномерная темперация придумана чтобы обеспечить свободу модуляций, например в фугах. А современному попо-року модуляции зачем, максимум временный тональный центр, в итоге идея оказалась почти никому не нужной…
  1. lair
    15.10.2019 21:34
    #20760054
    Равномерная темперация придумана чтобы обеспечить свободу модуляций, например в фугах.
    Вот только нужна ли она, ценой потери "хорошего" звучания (особенно в оркестре) и индивидуальности каждой тональности?
    
    Я могу понять, если бы речь шла о музыке ХХ века, там на это есть как минимум один утвердительный ответ, но вот применительно к XVIII я что-то не уверен.
    
    Druu
    15.10.2019 23:16
    #20760606
    +1
    Вот только нужна ли она, ценой потери "хорошего" звучания (особенно в оркестре) и индивидуальности каждой тональности?
    С оркестром-то какие проблемы, учитывая, что почти весь этот оркестр как играл так и продолжает играть либо в свободном строе (смычковые, вокал) либо в относительно-свободном (духовые)? Проблема-то только с пианинками, по сути. Но так и те иногда с розливом настраивают, чтоб больше мяса.
    А еще почти все инструменты на атаках завышают (весьма существенно иногда), так что при быстрой игре атакующими штрихами или с резкой динамикой вообще про строй можно забыть, там выше чем у темперации погрешности.
    Так что для оркестров шо темперировали шо не темперировали — все едино :)
    
    lair
    15.10.2019 23:17
    #20760612
    С оркестром-то какие проблемы
    Ну так ровно те, что не надо придумывать равномерную темперацию, чтобы обеспечить свободу модуляций, если оркестру на нее положить.
    
    Druu
    16.10.2019 09:00
    #20761826
    Ну так ровно те, что не надо придумывать равномерную темперацию, чтобы обеспечить свободу модуляций, если оркестру на нее положить.
    Так у оркестра в порядке все. Не в порядке у инструментов с фиксированным строем. Если вы, допустим, на скрипке хотите сыграть один и тот же интервал по-разному — то делаете это не отрывая смычка от струны. Проблемы просто не стоит. А на пианинке у вас только один вариант, в итоге либо вы темперируете, либо ограничиваетесь в музыкальном материале, чтобы, например, на волчью квинту не попасть. + регулярная перенастройка инструмента из тональности в тональность при смене материала. А настраивать пианинку — это тоже не колок подкрутить.
    Обратите внимание, "хорошо темперированный клавир", а не "клавир в хорошо темперированном строе". Инструмент темперированный. Не строй :)
    
    Ну и если виртуоз какой-то хочет, на самом деле, то может строиться как ему угодно.
    
    epishman
    16.10.2019 07:35
    #20761500
    С пианинками сплошные проблемы, по сути ни блюз ни джаз на них не звучит, поэтому и придумали всякие колесики, чтоб совсем из оркестра не выбросили :)
    
    polar11beer
    16.10.2019 18:15
    #20765306
    там на это есть минимум один утвердительный ответ
    А что это за ответ?
    
    lair
    16.10.2019 18:17
    #20765318
    Додекафония, для которой нужны независимые тона.
    
    polar11beer
    16.10.2019 19:00
    #20765526
    Спасибо, будем посмотреть что это за зверь
1. nihole Автор
  15.10.2019 21:49
  #20760156
  Знаете, я люблю фортепиано. Фортепиано именно так и настроено (равномерно темперированный строй). Приблизительность определяется ровно тем наскольо логарифм трех по основанию 2 отличается от 19/12. А это 0,1%. Поэтому в принципе, да можно услышать биения, но фальши я например не чувствую.
  3 не беру по тем же прчинам что и 1 (и любые нечетные числа) — квинта и кварта не попадут.
  1. lair
    15.10.2019 22:33
    #20760374
    +1
    Знаете, я люблю фортепиано.
    Ну то есть вы на самом деле ищете число, лежащее в основе музыки, которую вы любите и можете услышать, а не "современной музыки". Не слишком ли далеко идущие выводы вы делаете?
    
    Приблизительность определяется ровно тем наскольо логарифм трех по основанию 2 отличается от 19/12
    … а почему именно этих чисел?
    
    Поэтому в принципе, да можно услышать биения, но фальши я например не чувствую.
    Ну, вы не слышите. А люди до сих пор обсуждают достоинства и недостатки разных темпераций.
    
    3 не беру по тем же прчинам что и 1 (и любые нечетные числа) — квинта и кварта не попадут.
    Что значит "не попадут"? В равномерном двенадцатитоновом строе "квинта" тоже не попадает в чистую квинту.
    
    nihole Автор
    15.10.2019 22:59
    #20760530
    +1
    Ну вот смотрите. Например слушая Баха я не чувствую дигармонии, а вот слушая вот это произведение (чистый строй) эта дисгармония очень даже слышна. О чем спор? Слышно что интервалы в другой тональности (а не в той для которой были соблюдены все интервалы) звучат фальшиво.
    
    И это не потому что я привык к другому строю.
    В случае же равномерно темпрерированного строя искажение частоты (относительно чистого звучания) — проценты. Вы действительно это слышите?
    
    lair
    15.10.2019 23:05
    #20760570
    Например слушая Баха я не чувствую дигармонии
    И что? Если вы послушаете Баха в хорошей темперации, вы почувствуете дисгармонию?
    
    а вот слушая вот это произведение (чистый строй) эта дисгармония очень даже слышна
    И снова, о чем это говорит?
    
    О чем спор?
    О том, какие интервалы слышит и не слышит человек.
    
    В случае же равномерно темпрерированного строя искажение частоты (относительно чистого звучания) — проценты. Вы действительно это слышите?
    Я — нет, но у меня плохой слух. Но я слышу некоторые темперации лучше других.
    
    polos75
    16.10.2019 09:13
    #20761890
    Все слышат. Сравните трезвучие, взятое в равномерной темперации и в натуральном строе.
    
    excentrisitet
    16.10.2019 13:29
    #20763528
    Как-то в свой время послушал: youtu.be/Yqa2Hbb_els
    И пришёл к выводу, что лично мне равномерно темперированный строй нравится больше. Что натуральный звучит слишком стерильно, и без биений аккорд не приобретает, а наоборот, теряет свою привлекательность.
    Естественно не настаиваю на своей правоте. Это чистой воды вкусовщина.
    
    В одном из первых комментариев есть ссылка на микротональную музыку, и она зашла мне вполне нормально в том варианте, где аккорды чередуются по отдельности. А вот Пентатоника ни в одном варианте наоборот не понравилась. Кровушка из ушей течёт, как я не пытался услышать это хоть как-то «по-другому».
    
    polos75
    16.10.2019 14:19
    #20763848
    Мне немного жаль того, что до РТ разные тональности звучали по-разному. Музыканты могли, например, написать песню в определённой тональности потому, что она «лиричней».
    
    grayfolk
    16.10.2019 14:58
    #20764070
    Возможно, именно поэтому самые, к примеру, романтичные сочинения, писались в Ре-бемоль мажоре. Не задумывался раньше о таком )
    
    excentrisitet
    17.10.2019 09:32
    #20767740
    Не понял почему ссылка не сработала. Поправляю
    www.youtube.com/watch?v=Yqa2Hbb_eIs
  1. Refridgerator
    16.10.2019 06:05
    #20761350
    Знаете, я люблю фортепиано. Фортепиано именно так и настроено (равномерно темперированный строй). Поэтому в принципе, да можно услышать биения, но фальши я например не чувствую.
    А я наоборот, никогда не любил фортепиано — по причине того, что оно звучало как-то «неправильно». Не фальшиво, а скорее дисгармонично, сочетания нот в аккорде не складывались в единое целое.
    
    polos75
    16.10.2019 09:23
    #20761966
    Фальшь можно услышать при игре фортепиано с другими инструментами.
    Например, скрипка — безладовый инструмент, скрипач с хорошим слухом тяготеет к натуральной гамме и ему приходится подстраиваться под фортепиано (интонировать).
    Огромная работа проделывается для хорошей игры фортепиано с оркестром. Причём, со стороны оркестра. А хлопают больше пианисту )

apro
15.10.2019 21:56
#20760184
Вот нравилось нашим предкам число 12, у них везде 12: 12 месяцев
Немного непонятно, месяцы привязаны к обращение Луны вокруг Земли,
при чем здесь понравилось или не понравилось?
1. screwer
  16.10.2019 03:52
  #20761186
  Месяцев могло бы быть 15. Или 13. Или 10.
  1. playermet
    16.10.2019 11:41
    #20762812
    Каким образом? Цикл сезонов же повторяется приблизительно каждые 12 месяцев. Этот цикл назвали годом.
    
    screwer
    17.10.2019 13:30
    #20769320
    Вот именно что «приблизительно». Разобьём 365 дней на N интервалов, остаток равномерно припишем к существующим.
    
    Например с 15 месяцами в году будет по 24 дня в месяце. И только 5 из них будут на 1 день длинее остальных (в високосный год 6). А не ~ половина, как в случае c 12 месяцами.
    
    Аналогично 10 месяцев дадут 36 дней для одной половины месяцев и 37 дней для другой половины. Вообще разницы нет с 12 месяцами.
    
    haryaalcar
    18.10.2019 12:00
    #20774524
    Период смены фаз Луны 30 дней. За год таких периодов 12 — отсюда и пошло 12 месяцев. Иметь над головой счётчик времении — штука в бесконечность раз важнее, чем выровненные интервалы дней.
    
    lair
    18.10.2019 12:15
    #20774634
    … и поэтому каждое полнолуние приходится на один и тот же день месяца?
    
    haryaalcar
    18.10.2019 12:25
    #20774678
    Это уже дело десятое. Уходя в поход можно было сказать: «вернусь через одно полнолуние»
    А день месяца на небе не пишется. Все правки и реформы календаря были позже. Человек выше не понимал, откуда 12 месяцев.
    
    lair
    18.10.2019 12:26
    #20774690
    Все правки и реформы календаря были позже.
    И внезапно оказалось, что выровненные интервалы важнее, чем счетчик времени над головой?
    
    tabmoo
    18.10.2019 14:27
    #20775426
    -1
    Господа. Почитайте материалы про цивилизации Междуречья. Там найдутся ответы на ваши вопросы.

apapacy
15.10.2019 21:57
#20760188
+3
Если интересна история различных темпераций она изложена https://ru.wikipedia.org/wiki/%D0%A1%D1%80%D0%B5%D0%B4%D0%BD%D0%B5%D1%82%D0%BE%D0%BD%D0%BE%D0%B2%D1%8B%D0%B9_%D1%81%D1%82%D1%80%D0%BE%D0%B9
Как звучит строй в другой темперации (тож не натуральный можно хорошо представить по этому отрывку) https://youtu.be/ZJxfmhvVNQg?t=307 которая сделана посредством среднетоновой темперации https://ru.wikipedia.org/wiki/%D0%A1%D1%80%D0%B5%D0%B4%D0%BD%D0%B5%D1%82%D0%BE%D0%BD%D0%BE%D0%B2%D1%8B%D0%B9_%D1%81%D1%82%D1%80%D0%BE%D0%B9

Кстати это все в меньшей мере касается оркестрового звучания. Т.к. струнные инструменты не имеют темперации, а духовые хотя и фактически темперированы на сегодняшний день, но музыканты могут в достаточно широких пределах управлять высотой звучания.

И наконец, для любителей 1/4 тонов Эдиссон Денисов Пена дней https://youtu.be/OrEEjY9S_CU?t=547

lair
15.10.2019 22:56
#20760506
Что-то я внезапно задумался.

Возьмем отношение этих частот. Это отношение можно представить в виде произведения чисел a1^k1*a2^k2..., где ai— простые числа, а ki — целые числа [...] И чем эти простые числа (ai) меньше, тем гармоничнее для нашего уха будет звучать этот интервал (я нашел это утверждение тут (см. второй абзац)).
Ага, давайте достанем это утверждение: "Since the perception of consonance seems related to low numbers in the harmonic series, and 5-limit tuning relies on the three lowest primes, 5-limit tuning should be capable of producing very consonant harmonies". Запомним его.

Так, например, самым гармоничным звучанием в соответствии с этим утверждением будет являться октава (изменение частоты в 2 раза). А следующими по гармоничности интервалами будут квинта (изменение частоты в 3/2 раза) и кварта (изменение частоты в 4/3 раза).
Но четыре — не простое число. И чистый строй не использует кварты, он использует октавы (степени двойки), квинты (степени тройки) и большие терции (степени пятерки).

Что как бы говорит нам, что требование иметь в строе квинту и кварту — оно произвольно.

(я, на самом деле, за кварту зацепился еще при первом прочтении, потому что кварта, субъективно — не консонантный интервал, она консонантна только как обращение квинты)
1. nihole Автор
  15.10.2019 23:04
  #20760560
  Если вы имеете квинту (до соль), то вы имеете и кварту (соль до)
  Поэтому частота интервала кварты это просто 2:3/2 = 4/3
  Далее в силу условия инвариантности вы должны иметь тот же интервал и от до (а не только от соль)
  1. lair
    15.10.2019 23:13
    #20760602
    Если вы имеете квинту (до соль), то вы имеете и кварту (соль до)
    Конечно, нет. С чего вы взяли, что если у вас есть некий интервал А, то его дополнение до октавы ему равноправно?
    
    Далее в силу условия инвариантности
    Которое условие вы взяли произвольно.
    
    nihole Автор
    16.10.2019 00:23
    #20760866
    Я перестаю вас понимать
1. 0xd34df00d
  16.10.2019 04:24
  #20761220
  Четыре — это квадрат простого числа, соответствующее k равно двум. А вот что гармоничнее, 4/3 или 5/2 — вопрос.
  
  Но это я так, в теории музыки я как свинья в апельсинах. Надену-ка я дальше наушники с правовыми Reflections.

apapacy
15.10.2019 23:05
#20760566
То есть наряду с тоникой с частотой и октавой с частотой у нас также должны быть квинта и кварта, с частотами соответственно, или что-то очень близкое, что мы ...
Долго не мог понять Ваш ход мыслей, теперь становится яснее. Если уже брать за основу самые благозвучные интервалы то лучше брать октаву 2/1 и квинту 3/2. Что и дела Пифагор. Тогда получаем что откладывая квинты вверх и октавы вниз мы возможно придем к числу близкому к единице. И это так 3^12/2^19=1.0136432647705078
Но если мы послушаем музыку Востока. То услышим что у них совершенно другой строй.

По поводу равномерной темперации, мы просто привыкли к такому строю поэтому он нам кажется идеальным. Плюс для этого строя написаны произведения начиная с Баха и до наших дней. Во времена Баха и до него этот строй воспринимался как фальшивый. Особенно это касалось органа у которого вместо прозрачного звучания начались акардеонные "розливы". Тем более что вопрос о применении строя решали великие музыканты которые это все воспринимали гораздо ярче чем простые прихожане.
1. nihole Автор
  15.10.2019 23:12
  #20760600
  Как только мы берем квинту и октаву мы сразу получаем и кварту
  Например, квинта до(первой октавы) — соль сразу нам дают кварту соль — до (второй октавы)
  Далее в силу инвариантности (все интервалы должны быть одинаковы для любой основы) мы так же должны иметь и кварту от основного звука (в данном примере от до)
  1. apapacy
    15.10.2019 23:29
    #20760658
    +2
    В этих рассуждениях есть несколько моментов которые более похоже на анализ "задним чисолм" Во-первых ни из чего не следует что все интервалы должны быть одинаковы. Во-вторых, ни из чего не следует что игра в до мажоре должна звучать как игра в ре мажоре без перенастройки инструмента. Раньше например у каждого трубача было несколько труб на которых он играл в зависимости от тональности. Ну и то что разбиение на 12 тонов является заданной величиной также опровергается практикой не западно-европейской музыки.
    Я даже скажу больше. Если в 19 веке при записи народных песен на территории России обычно пользовались 12-тонным звукорядом и отклонением от него считали "фальшивым" пением. То в 20-м веке появился интерес усложненной во всех смыслах музыке 20-века и фольклористы наконец "услышали" что в разных регионах России существует свой строй и начали записывать уже со всякими диакретическими знаками все это.
    
    nihole Автор
    16.10.2019 00:02
    #20760804
    Да, конечно, все это существует.
    Но давайте возьмем, например, любимый многими «Hotel California» Eagles.
    Сплошной квинтовый круг. Вы смещаетесь на квинту и повторяете одну и ту же музыкальную фразу. Потом еще раз на квинту — и опять повторяете, потом еще раз…
    И эта фраза должна звучать одинаково, иначе будет не гармонично.
    
    Вот это современная музыка (в моем представлении). Вы постоянно меняете тональность, смещаетесь и все должно звучать так же. Я в статье это называю инвариантностью. Это можно добиться только равномерным темперированием (нет?)
    
    Конечно, если ваша музыка другая и не подразумевает таких модуляций, то в этом нет необходимости. Но это не современная (европейская) музыка или во всяком случае не мейнстрим.
    
    lair
    16.10.2019 00:08
    #20760828
    +3
    И эта фраза должна звучать одинаково, иначе будет не гармонично
    … и при этом, если она везде звучит одинаково — это, внезапно, бедно. Собственно, это один из двух основных аргументов против равномерной темперации.
    
    Вот это современная музыка (в моем представлении). Вы постоянно меняете тональность, смещаетесь и все должно звучать так же. Я в статье это называю инвариантностью. Это можно добиться только равномерным темперированием (нет?)
    Нет. Достаточно иметь инструмент с подвижным основным тоном, вокруг которого темперация может быть любая. Самый простой доступный пример — гитара, на которой (правильно написанная) фраза может играться в любом месте лада, везде звучать одинаково, нигде при этом не будучи равномерной.
    
    lair
    16.10.2019 02:52
    #20761140
    может играться в любом месте лада
    В любом месте грифа (ака на любом ладу), конечно же. Отвлекся.
    
    Druu
    16.10.2019 13:08
    #20763386
    … и при этом, если она везде звучит одинаково — это, внезапно, бедно.
    Совсем нет. Вы рассуждаете как человек, который привык к рт, т.е., для вас вот есть некоторые ноты и они дают какие-то интервалы. На самом деле-то ситуация исторически обратная — в первую очередь существуют интервалы, и эти интервалы уже дают какие-то "ноты" (места где струну зажать, условно). С этой точки зрения, если у вас есть какая-то мелодия, то конечно она при смещении на квинту должна звучать точно так же (т.е. представлять ту же самую интервальную последовательность), и для любого музыканта было бы удивительным, если это вдруг не так.
    Все разговоры про "особенности звучания конкретной тональности" — это вообще веяния современности, когда возникла необходимость в темперации (с распространением инструментов фиксированного строя), и это ни что иное как заметание мусора под ковер.
    
    нигде при этом не будучи равномерной.
    Так гитара в рт строится. Если вы настроите ее в другом строе, то тогда фраза не будет звучать одинаково при движении по ладам.
    
    lair
    16.10.2019 13:23
    #20763488
    +1
    Вы рассуждаете как человек, который привык к рт
    Нет, я рассуждаю как человек, которому надоело развитие через повторы, и хочется чего-то более другого.
    
    С этой точки зрения, если у вас есть какая-то мелодия, то конечно она при смещении на квинту должна звучать точно так же
    А потом внезапно мы встречаемся с полифонией, где в одном голосе фразу сместили на некий интервал, а в другом — не сместили, и интервалы между этими голосами нас тоже волнуют.
    
    для любого музыканта было бы удивительным, если это вдруг не так.
    Неа. Если бы для любого музыканта это было удивительно, не было бы никакой семантики тональности. А она есть (ну, для некоторых людей, по крайней мере).
    
    Так гитара в рт строится.
    Это, скажем так, не обязательно.
    
    Если вы настроите ее в другом строе, то тогда фраза не будет звучать одинаково при движении по ладам.
    Вы можете иметь равномерно настроенные лады, но неравномерно настроенные струны. Тогда если вы делаете транспозицию только сменой позиции, у вас будет сохраняться внутренняя темперация фразы.
    
    Druu
    16.10.2019 14:35
    #20763938
    Нет, я рассуждаю как человек, которому надоело развитие через повторы, и хочется чего-то более другого.
    Можно и без повторов. Только строй тут при чем?
    
    А потом внезапно мы встречаемся с полифонией, где в одном голосе фразу сместили на некий интервал, а в другом — не сместили, и интервалы между этими голосами нас тоже волнуют.
    Ну так вот при равномерной темперации вы просто сместили — и все, у вас между всеми соответствующими нотами будет один и тот же интервал. А в противном случае — получатся разные, но тогда это уже не смещение. В неравномерном строе вы не можете в принципе взять и поднять/опустить голос, т.к. получится откровенная лажа.
    
    Неа. Если бы для любого музыканта это было удивительно, не было бы никакой семантики тональности.
    Как раз наоборот — если бы при смене тоники тональности бы меняли звучание, то семантика тональности бы и терялась. Функциональность ступеней существует именно потому что все тональности звучат одинаково. С-но, все музыканты всю жизнь при смещении играли те же самые интервалы. Все рассуждения о "каждая тональность звучит по-своему" — это вообще веяние времени, которое появилось и умерло. Никаких исторических предпосылок или чего-то такого у этого веяния не было, это был просто способ выдать баг за фичу.
    
    Вы можете иметь равномерно настроенные лады, но неравномерно настроенные струны. Тогда если вы делаете транспозицию только сменой позиции, у вас будет сохраняться внутренняя темперация фразы.
    В пределах одной струны у вас тогда строй будет темперированный. А на нескольких — да, при смещении, между ладами интервалы будут сохраняться. только это будет не строй вообще — а сплошная фальшь и лажа, т.к. каждая струна у вас будет в своем собственном строе, по факту.
    
    Т.е., в принципе, на этом даже можно будет играть — либо мелодии на одной струне, либо аккорды "одним пальцем", но на этом и все.
    
    apapacy
    16.10.2019 00:26
    #20760876
    +2
    Это все называется культура в которую темперированный строй был включен и мы были на этом строе воспитаны. В конце концов у Eagles один тоько «Hotel California». А индийские фильмы все такие https://www.youtube.com/watch?v=YUVCOK11MF8
    
    К сожалению у многих народов слух уже испорчен попсой и дешевыми электронными инструментами. так что в фиьмах 90-х и позже такого лада вы уже не услышите. В этом плане показательно что если в ранний период в Болливуде пели и танцевали (и играли роли) одна и та же актриса. То в 90-е пели за них бабушки у которых еще остался характерный для индийской музыки строй. Хотя наверно где-то в провинции все как и сто лет назад у них.
    
    nihole Автор
    16.10.2019 00:39
    #20760918
    Я не являюсь защитником или противником никакого строя
    Я говорю лишь, что равномерно темперированный строй (и его я считаю основой современной европейской музыки) возможен лишь благодаря тому что логорифм трех по основанию 2 с хорошей точностью равен 19/12. Это же и определяет то почему у нас 12 полутонов в октаве.
    
    Я думаю весь спор сейчас связан не с этим, а с тем что я называю равномерно темперированный строй основанием современной (европейской) музыки.
    
    Ну, вот я так считаю. Вы судя по всему нет.
    
    apapacy
    16.10.2019 00:49
    #20760954
    Ну это так просто исторически сложилось и имплементировалось в нашу культуру. Но ничего имманентного в этом нет. Возможно что Пифагор также со своими расчетами не последнюю роль в этом сыграл.
    Плюс нужно учесть что хорошо темперированными являются только некоторые инструменты с фиксированной высотой (клавишные, гитары с ладами, балалайки) а все остальные например струнные, человеческий голос — исполнят музыку в согласно внутреннему слуху музыканта, который не является темперированным. И постоянно находится в движении. Например, если Вы послушаете старинные записи лучших оркестров мира, то можете услышать что их лад немного отличается от современного и мы это воспринимаем как погрешности в интонировании.
    
    Кстати про инструменты с ладами. За счет большего или меньшего прижатия струн а иногда и смещения струны музыканты иногда подсознательно "дотягивают" высоту звука до своего внутреннего слышания.
    
    lair
    16.10.2019 00:56
    #20760968
    За счет большего или меньшего прижатия струн а иногда и смещения струны музыканты иногда подсознательно "дотягивают" высоту звука до своего внутреннего слышания.
    Я бы, сугубо по личному опыту, сказал "часто", а не "иногда".
    
    chupasaurus
    16.10.2019 16:51
    #20764768
    А ещё есть fan fret грифы, прямые ладов в которых не перпендикулярны грифу и сходятся в точке под 12-м ладом, в следствие чего усилие для зажатия струны для точного попадания будет индивидуальным для каждого лада.
    
    Kinardus
    16.10.2019 18:07
    #20765256
    Всё прочитал, но так и не понял, откуда число 19.
    Простите, если не внимателен.
    
    nihole Автор
    16.10.2019 18:28
    #20765378
    К сожалению не получается писать формулы в комментариях.
    Там есть в основной формуле, что
    2*логарифм 3 по основанию 2 — 3 = 0,170 что приблизительно = 1/6
    отсюда и получается что логарифм 3 по основанию 2 приблизительно равен 19/12 ((1/6 +3):2)
    
    fesst
    17.10.2019 01:04
    #20766876
    7/12 — степень, в которую надо возвести sqrt(2, 12) чтобы получить темперированную квинту. 19/12 = она же + октава (12/12 или 1)
    
    lair
    16.10.2019 00:41
    #20760928
    Хотя наверно где-то в провинции все как и сто лет назад у них.
    А у нас в провинции при этом вполне может быть так, что в качестве народных песен поется авторский тюремный романс начала века. Или, что хуже, просто песня из радио, "потому что на свадьбах просют пети". Естественно, за все провинции сказать не могу, но это — из конкретной поездки под Вятку в первой половине двухтысячных.
    
    apapacy
    16.10.2019 00:56
    #20760964
    В Индии провинция гораздо провинциальней. Один из моих сотрудников ездил в Индию на предприятие авиапрома. Неквалифицированный обслуживащий персонал там жил рядом на горе в роще в картонных домиках. Но это же авиапром. А что говорить о глубинке.
    
    0xd34df00d
    16.10.2019 04:31
    #20761228
    Но давайте возьмем, например, любимый многими «Hotel California» Eagles.
    Сплошной квинтовый круг. Вы смещаетесь на квинту и повторяете одну и ту же музыкальную фразу. Потом еще раз на квинту — и опять повторяете, потом еще раз…
    Тру металлисты вообще опускают шестую струну (если у них всего шесть струн) на полтона, чтобы одним пальцем елозить и выдавать сочни вздрыжни квинты под дисторшном. Не понимаю, какой вывод из этого можно сделать.
    
    polos75
    16.10.2019 09:20
    #20761950
    Чтобы одним пальцем — это на тон ниже )
    
    0xd34df00d
    16.10.2019 19:06
    #20765554
    Тьфу ты, вот что значит шесть лет гитару в руки не брал.
    
    KReal
    16.10.2019 19:04
    #20765548
    некоторые нетру джентеры опускают шестую в октаву с пятой, вообще сок)
    
    0xd34df00d
    16.10.2019 19:06
    #20765556
    Правильно, у тру джентеров после шестой струны ещё две есть.

SADKO
16.10.2019 01:47
#20761086
+3
Ребята, это позорище, мы живём в 21 веке, играем на всяких синтезаторах и сэмплерах, продолжая использовать позорное лигаси, равномерно темперированный строй! И ещё какие-то причины в защиту этой подлости пишем.

Нужно взглянуть на вопрос в историческом контексте и всё сразу станет по местам. РТ не от хорошей жизни придумали, поди перестрой орган или фортепиано, но сегодня с этим нет проблем.

Если уж и привлекать аналитику, то обратите внимание как рок и более тяжёлая музыка тяготеет к конкретным тональностям, хотя они вроде бы и равнозначные. А вся фигня в том, что инструменты имеют физические ограничения, и искажения тоже имеют физическую природу, и крутых последовательностей звуков во всём этом кажущемся многообразии не так уж много.
У синтезаторов нет физических ограничений, но взаимоотношения РТ и искажений тянут авторов туда-же.

Так может хватит страдать мозахизмом, и двинуться в сторону чистых интервалов.
Тем более что есть алгоритмы правящие интервалы на лету, так что можно с кайфом поиграть РТК Баха.

PS. А по поводу странностей звучания чистых интервалов, так это от загаженности мозга только. Вы поиграйте на расстроенной гитаре, пара песен, и вы уже воспринимаете её как должное и поёте также криво. И самый кайф тут включить радио, и по слушать как там всё внезапно окривело.
So, математика это хорошо, но в музыке решает физика и физиология восприятия.

Pps. а если говорить о популярной евро музыке то там сплошная диатоника, которой ничто не мешает быть чистой.
1. polos75
  16.10.2019 09:18
  #20761926
  Полностью согласен.
  Не зря же выдумывали фортепиано с удвоенным количеством чёрных клавиш, а гитаристы подрезают лады для натуральных аккордов.
  Аналоговый мир ограничен и с цифрой пора придумывать музыку заново. Просто у нас нет фигуры размера Баха.
1. Druu
  16.10.2019 10:01
  #20762186
  Нужно взглянуть на вопрос в историческом контексте и всё сразу станет по местам. РТ не от хорошей жизни придумали, поди перестрой орган или фортепиано, но сегодня с этим нет проблем.
  Проблема не в этом, а в том, что перестраивать надо не между исполнениями и даже не в процессе — а во время взятия одного аккорда, что невозможно логически. Т.е., существуют аккорды, которые нельзя сыграть чисто ни в каком строе. Вообще. Как ни настраивай. Просто не существует набора нот, из которого можно составить чисто звучащий аккорд с данной формулой. Потому что если будет чистый интервал, например, между 1 нотой и 2, 2 и 3, 3 и 4, то получается грязь между 1 и 4. А сделаем чисто между 1 и 4, будет грязь, между 2 и 3. И так далее. В итоге варианта три:
  
  вообще такие аккорды не играть (как это и делали до появления рт)
  
  сильно фальшивить на каком-то из интервалов
  
  слегка фальшивить на всех
  
  так вышло, что чисто практически лучше звучит, когда немного фальшивы все интервалы, чем когда все кроме одного звучат чисто, а с одним оставшимся — совсем беда.
  
  иными словами, у нас есть следующий вопрос: "если у нас есть аккорды, которые, математически, невозможно играть без фальши, то как нам играть их с наименее заметной фальшью?", ответ: рт.
  1. polos75
    16.10.2019 10:44
    #20762438
    Если оставаться в пределах одной тональности — можно сделать вообще без фальши. Но при переходе в другую придётся заново пересчитывать ступени.
    
    Druu
    16.10.2019 11:03
    #20762556
    Если оставаться в пределах одной тональности — можно сделать вообще без фальши.
    Нет, нельзя. Натуральный строй дает волчьи квинты даже в пределах одной тональности. Кроме того, "оставаться в одной тональности" — это чрезмерно сильное ограничение. И, как я выше уже сказал — перестройка после перехода в другую тональность вам никак не поможет, т.к. аккорд ни в какой тональности и ни в каком строе не будет играться без фальши. Просто нет математически таких нот, чтобы без фальши сыграть. Нет их. Это одно дело если вы играете на мелодических инструментах, а если у вас пианинка, где в норме по 5+ кнопок жмут — то это совсем другое. Ввести подобные ограничения = де-факто убить пианинку как инструмент. Нетемперированная пианинка просто не играет, это не инструмент.
    
    SADKO
    16.10.2019 12:14
    #20763038
    Ну, первично я сам вообще-то клавишник, правда органист, а не фортепьяница, не суть. Я просто оставлю это тут arxiv.org/abs/1706.04338 и justintonation.tp3.app — это просто для приемра, на попробовать, ибо это сильно быстрее чем, что-то объяснять…
    
    смысл over 12 EDO я и сам вкурил только тогда когда мне пришлось петь, и то не сразу. Как последний лох я настраивал гусли по хроматическому тюнеру. И только по мере освоения безладовых струнных, я наконец понял, что-же именно мне здесь не нравится.
    
    Тут ещё интересный момент, нюансировки, тон движущийся к\от сетки строя, несёт семантическую нагрузку, так-же как и смещения относительно ритмической сетки.
    
    apapacy
    16.10.2019 14:42
    #20763956
    Я с Вами и согласен и не согласен. Согласен в том что инструмент с фиксированным строем возможен только с темперацией. Не обязательно с равномерной темперацией. Другие варианты тоже звучат в простых тональностях хорошо но при модуляциях начинают сильно фальшивить. Но есть и другая часть вопроса. Это кто и как делает темперацию. Если это математически просчитанная и реализованная аппаратно гамма то она звучит очень бедно и такое впечатление что каждый звук немного фальшивит.
    
    Но когда настройкой инструмента занимается настройщик (если он хороший настройщик) то его темперация отличается от равномерной на какие-то проценты. В результате чего строй становится более приятным.
    
    Я в юности занимался настройкой фортепиано и могу примерно это процесс описать. По камертону настраивается ля 1-й октавы. После этого идем по квинто-квартовому кругу ля вниз ре вверх соль вниз до вверх фа вниз си-бемоль вверх ми-бемоль вверх ля-бемоль вниз ре-бемоль вверх фа-диез вниз си вверх ми вниз ля малой октавы которое при правильной темперации должно сойтись в октаву с исходным ля.
    
    При этом в процессе не используются какие-то вспомагательные устройства. начинающие настройщики иногда считают биения. Но это не очень точно. Во-первых биентия хорошо слышны только в квинтах, т.к. их нужно считать между 1-й и 2-й гаромоникой. В квартах же считают между биения между второй и третьей что на слух сложнее сделать. Плюс в зависимости от выстоты исходных звуков частота биений также меняется и их точные отсчет без спец приборов также невозможен без хронометра. Поэтому настройщики как правило темперируют кварты и квинты по тембру их звучания. Так что хорошо настроенный рояль хорошим настройщиком это также своего рода произведение искусства. И отличается от математически строгой равномерной темперации ровно настолько чтобы мы не слышали фальши.
    
    Druu
    16.10.2019 15:36
    #20764324
    И отличается от математически строгой равномерной темперации ровно настолько чтобы мы не слышали фальши.
    Математически строгая темперация говорит о том, как должен быть выстроен процесс темперации — им настройщики и пользуются. Но реальное фортепиано — оно не математическое, в частности, обертоны струн не кратны в точности основному тону, т.к. струны имеют ненулевую толщину. Это и дает расхождения, увеличивающиеся с каждой октавой.
    
    Тут, в общем-то, нет никакого противоречия, это все та же равномерная темперация.

Dr_Faksov
16.10.2019 07:59
#20761554
О как! Представляется мне, что автор — истинный математик. Взяв сушествующее явление, он попытался сделать «реверс инжиниринг» чисто математическими средствами.
Отбросив физику звучания струн и воздушных столбов (гармоники и обертона), физиологию (не все звуки одинаково приятны) и европейскую историю нотной записи ( 7 нот ) он получил число.
А если учесть, что музыкальный строй строится, в первую очередь, на физике и физиологии то выглядит это несколько странно.
1. juramehanik
  16.10.2019 10:02
  #20762192
  Хотелось бы на счет физиологии подробнее.
  Вообще тут столько интересных комментариев, особенно от lair, что тянет уже на отдельную статью)
  1. SADKO
    16.10.2019 13:08
    #20763376
    Хотите физиологии, пожалуйста, можно нагуглить графиков разрешающей способности слуха по частоте, она падает с ростом частоты, что обусловлено конструктивными особенностями улитки и слухового нерва. Но дальше начинаются «чудеса», это разрешение anyway больше чем позволяет физическое количество нервов.
    Секрет в том, что механическая трансмиссия от барабанной перепонки к стремени улитки, даже чистую синусойду загадит\обогатит гармониками с частотами кратными. А мозг другой реальности и не знает, и приспособился ощущать изменение частоты по более низким гармоникам оного.
    И это не какая-то придумка, а конкретная физиология, более того, есть куча психоакустических приборов и алгоритмов работающих на понимании этого принципа.
    Например мы можем частоты за 80 герц отрезать, исказить или рассчитать вторые гармоники обрезка, и добавить их в микс. А слушатель заметит разницу разве что тактильно, что басы не колышут, и не обдувают, но они ЕСТЬ, даже из переделок не играющих эти частоты. Такое колдунство.
    
    А если вернуться к теме, то автор рассматривает погрешности отношения стерильных тонов, а для человека таких просто не бывает. И если на основной частоте всё вроде-бы и ништяк, то из гармоник образуются срачи. Помню был ещё один такой умник, в веках, Пифагор звали. У него были правильные уши, так что борясь за чистоту строя, он не стал загаживать каждый интервал корнем, а слил в октаву все помои.
    Тоже был варинат, для не многострунных античных инструментов и голоса годный, но чуть более полифонии, и начиналась содомия.

nonpar
16.10.2019 08:09
#20761590
К числу 12 можно прийти и без длительных расчетов. Дюжина как счетная единица употреблялась издавна, потому что 12 — число, имеющее 3 минимальных последовательных делителя: 2,3 и 4. С точки зрения звукоизвлечения, это важно для образования обертонов. Следующее подобное число — 60. Оно тоже издавна применялось, как счетная единица, но 1/60 октавы — это слишком тонко, как для человеческого слуха/речевого аппарата, так и для настройки музыкальных инструментов.
1. mapron
  16.10.2019 09:13
  #20761892
  +1
  имеющее 3 минимальных последовательных делителя: 2,3 и 4. С точки зрения звукоизвлечения, это важно для образования обертонов
  
  Это не так работает. 12 это не линейная величина по частоте, а логарифмическая, обертоны вообще ни при чём.
  1. nonpar
    16.10.2019 11:36
    #20762798
    Вы приписали мне идею про линейность, которую я не высказывал)
    Во-первых, обертоны ближайших нечетных гармоник (третьей и пятой) должны быть максимально приближены к основным тонам следующих октав, чтобы не диссонировать с ними. Для разбиения октавы на 12 это выполняется.
    Во-вторых, подумайте, откуда взялись понятия о благозвучности интервалов, приведенные в вики-статье, на которую вы ссылаетесь? То, что ряд интервалов и гармоник, присущий разбиению на 12, наиболее оптимален с точки зрения минимизации диссонансов — тоже, предположительно, математическое следствие непрерывности ряда делителей для числа 12. Строго доказывать это, впрочем, я не возьмусь. Если я прав — это наверняка давно сделано, а если неправ — то неправ.
    
    mapron
    16.10.2019 16:57
    #20764806
    Хорошо, допустим, вы правы. Как тогда получается, что и для разбиения на 19 интервалов это все работает (даже еще лучше)? :)
    Разбиение и близость к квинте/терции — да. Делители числа — нет.

AlexzundeR
16.10.2019 09:04
#20761838
А с точки зрения частот и разложения в тональный ряд, 8-битная музыка, что из себя представляет? Послушал 53-тональную музыку от Sevish и услышал много знакомых мотивов. По идее, врядли получилось добиться равномерного темперирования от апроксимации.
P.S. Спасибо за статью и за интересные комментарии к ней.
1. mapron
  16.10.2019 09:22
  #20761958
  Ощущение, что ваше представление слегка поверхностно, без обид.
  
  8-битная музыка накладывает по сути ограничение на богатство тембра, на сложность дополнительных обертонов, т.е. ноты звучат примитивно (в нейтральном смысле), нет многообразия красок как в «ламповой акустике». С точки зрения частот — ну, их в разложении всяко будет меньше, чем в живой записи. С точки зрения строя — это вообще никак не применимо. У меня подозрение, что большинство чиптюнов записано все же в классическом 12-тоновом строе.
  
  Послушал 53-тональную музыку от Sevish и услышал много знакомых мотивов
  
  Ну так никто и не утверждает что сама мелодия должна как-то радикально иначе звучать. Если ваше ухо интервалы меньше 1/4 тона не различает, вам по идее без разницы, какая тональная система используется. В идеале, у вас может возникать ощущение «слегка расстроенных инструментов» из-за непривычности, если вы занимаетесь музыкой давно.
  1. AlexzundeR
    16.10.2019 11:44
    #20762838
    Ну я скорее про инструменты в 8-битной музыке и спрашивал, понятно, что диапазон частот потенциально доступен практически весь с некоторыми апроксимациями.
    Т.е. на чиптюнах настраивают стандартный 12 тоновый строй?
    Мне как раз показалось, что синтетика позволяет использовать композиторам и промежуточные тоны. Тогда зачем привязываться к привычным устоям?
  1. shiru8bit
    16.10.2019 13:28
    #20763522
    +1
    В чиповой музыке есть свой вопрос строя, даже наверное более актуальный, чем на пианинах и гитарах. Это даже одна из ключевых характеристик чиповой музыки (элемент её узнаваемости), хотя и не такая заметная, как примитивные тембры и использование арпеджио.
    
    Принцип работы звуковых чипов в делении входной тактовой частоты на целый делитель, разрядность которого ограничена (бывало 5, 8, 10, 11, 12, 16 бит), а это даёт очень ограниченный набор возможных частот, каждая из которых толком не попадает ни в одну ноту ни в одном строе, причём чем выше частота, тем меньше точность. И нужно придумать, как получить такую таблицу приближённых частот нот, чтобы на ней прилично звучало хоть что-то. Основные подходы — сгенерировать таблицу чисто математически под равномерно темперированный строй с округлением, и игнорировать нестрой (либо специально сочинять вокруг него так, чтобы звучало приятно), либо подбирать каждую частоту каждой ноты индивидуально на слух или из иных соображений.
    
    Dr_Faksov
    17.10.2019 06:50
    #20767208
    Ну зачем вы так — «делении входной тактовой частоты на целый делитель». Делитель частоты с дробным коэффициентом деления изобретен в прошлом веке. Смотрите, к примеру патент СССР 750744 за 78 год. Именно такие применялись и применяются в ЭМИ для получения звучания нужных нот.
    
    shiru8bit
    17.10.2019 14:21
    #20769652
    Я говорю совершенно конкретно про чиптюн и звуковые чипы в старых приставках и компьютерах, а не про ЭМИ и не про СССР. Никаких дробных делителей там нет.
    
    Dr_Faksov
    18.10.2019 01:48
    #20773050
    Извините, прочитал невнимательно.

matraskin
16.10.2019 09:14
#20761904
… Может быть это просто случайность? Вот нравилось нашим предкам число 12, у них везде 12: 12 месяцев, 12 знаков зодиака, 12 колен Израилевых, 12 апостолов,… и здесь решили, пусть будет 12, и так и повелось. Или все же здесь есть объективный закон, и это число не случайно?…

Как вариант — раньше модно было все на 12 делить, вот и в музыке поделили октаву на 12 частей.
Если бы в наше компьютерное время поделили бы на 16.
1. math_coder
  16.10.2019 09:53
  #20762134
  Нет, 16 не годится. Вы статью-то читали? Хоть позиция автора странновата, и название статьи отражает лишь крайне слабое знакомство автора с именно современной музыкой, но по сути-то всё верно.

python273
16.10.2019 10:16
#20762282
Видео в тему

Where does the 12-tone scale come from?
https://www.youtube.com/watch?v=CFbG-8eYKJU

click

KvanTTT
16.10.2019 12:17
#20763066
Вот мне интересно: а можно ли где-нибудь почитать и послушать музыку с "идеальным" строем, т.е. где частоты бы подбирались в зависимости от используемых вместе нот, от аккордов. Хотя ее невозможно будет сыграть на привычных клавишах, т.к. особого строя то и не будет, точнее он будет непрерывным, а не дискретным. Ну хотя бы синтезированную.
1. apapacy
  16.10.2019 12:45
  #20763222
  Обратите внимание что вся музыка не электронная р не клавишная такая и есть. Если конечно у музыкантов высокая квалификация. Темперация относится к инструментам с фиксированным строем
  1. KvanTTT
    17.10.2019 10:17
    #20767946
    Неправда: струнные ладовые, большинство духовых имеют равномерно темперированный строй. А в электронной как раз можно сделать любой строй.
    
    Druu
    17.10.2019 10:27
    #20767986
    большинство духовых имеют равномерно темперированный строй
    Он в духовых, скажем так, темперированный формально. На практике, для большинства духовых музыкант может достаточно сильно отклоняться от заданной ноты.
    
    Струнные ладовые только те, которые ладовые :)
    Как минимум, почти все смычковые — безладовые.
    
    С ладовыми тоже нюанс — вибрато на акустической гитаре делается так же как на скрипке, т.е. вдоль струны, а не бендом. Если бы лад жестко фиксировал высоту звучания, то это было бы невозможно.
    
    А в электронной как раз можно сделать любой строй.
    Это в теории. А на практике, традиционно, в электронной музыке работают с тембральными характеристиками. Всякие интересные семплы и вот это вот.
    
    Так что, все иногда не совсем так, как кажется :)
    
    lair
    17.10.2019 11:39
    #20768376
    струнные ладовые,
    Расскажите это всем струнным с навязными ладами (например, виоле да гамба)
1. Refridgerator
  17.10.2019 07:13
  #20767248
  Я слышал о таком проекте, но навскидку название не вспоминается. Мне также представляется возможным автотюнинг при игре на клавишах вживую, если дополнительно (например, ногами) указывать текущий аккорд и его роль в гармонии. То есть при обыгрывании (в одной и той же тональности) ля-минора один тюнинг, до-мажора — другой, до-мажора после ля-минора — третий.

mazkorulez
16.10.2019 12:21
#20763094
+1
Вопросы к автору на тему его расчётов.
1. Не ясно, что мы пытаемся сделать — найти звукоряд или определить количество звуков?
2. Зачем при этом ставить в качестве цели подгонку («Мы хотим показать, что N при наших условиях должно равняться 12»)? Условия выражены не явно (наверное, потому что задание выражено не явно).
3. Что вы имели ввиду написав " интервал между частотами соседних звуков должен быть одинаковым и должен быть равен 2^(1/N)"? На самом деле нельзя сказать, что оно является следствием второго требования, т.к. ваше «второе требование», которое местами превращается во второе «условие», так и не было формализовано.
4. Почему вы пишете что «изменение частоты» между двумя звуками для вас тоже самое, что «отношение частот»?
5. Почему в соответствии со вторым условием отношение 3/2 к 4/3 также должно быть 2^(n/N)? Мы вроде что-то писали про 2^(1/N)?
6. Если n = 3/2 w0 — 4/3 w0 = 1/6 w0, то почему при подстановке в формулу n = N *0.170 мы получаем N=6i?
Советую вам ещё раз посмотреть, что вы ищете, использовать одинаковую терминологию на протяжении всей статьи, проверить все обозначения и все формулы.
1. nihole Автор
  16.10.2019 12:26
  #20763122
  Вы пытаетесь найти ошибку в расчете?
  Ее как мне кажется нет. Это очень простая математика. Если сделать те предположения, которые я сделал, то получится то, что я получил.
  
  Отвечу на ваши вопросы чуть позже.

rtkprg2
16.10.2019 12:21
#20763100
Мое имхо почему 12:
это число с одной стороны дает довольно хорошую градацию (не много и не мало), а с другой стороны оно хорошо делится: на 2, на 3, на 4, на 6.
1. lair
  16.10.2019 13:27
  #20763512
  а с другой стороны оно хорошо делится: на 2, на 3, на 4, на 6.
  А для музыки-то это чем полезно?

toivo61
16.10.2019 14:56
#20764062
12 полутонов в октаве, это еще и эргономически-технологическое ограничение.
Если гитару 24 четверть тоновую еще представить можно, но фортепиано с 19-ю клавишами на октаву уже трудно.
1. grayfolk
  16.10.2019 15:21
  #20764260
  К сожалению, не могу сейчас нагуглить, в детстве читал — может и напутал что.
  Александр Скрябин был абсолютником и не переносил равномерную темперацию.
  Поэтому заказал себе рояль с дополнительными клавишами, где до-диез не был энгармонически равен ре-бемолю. Ну и остальные энгармонизмы тоже.
  1. Druu
    16.10.2019 16:38
    #20764678
    Александр Скрябин был абсолютником и не переносил равномерную темперацию.
    Звучит странно, учитывая, что абсолютный слух как раз на то и абсолютный, что ему пофиг на интервалы (не говоря уже о том, что абсолютных слух сам по себе обычно очень неточный и многие абсолютники ошибаются на четвертьтон и больше), если вы привыкли что нота звучит определенным образом — то вы и привыкли. Т.е. чтобы "не переносить" равномерную темперацию надо с детства (когда формируется абсолютных слух) привыкать к нетемперированному строю, что выглядит совсем невероятным, т.к. Скрябин был пианистом.
    Другое дело, если у него был очень хорошо организованный относительный слух (ну, как и было :)).
    
    grayfolk
    16.10.2019 16:41
    #20764704
    абсолютный слух как раз на то и абсолютный, что ему пофиг на интервалы
    
    Поспорю, у меня есть друзья-абсолютники, которых как раз интервалы и коробят.
    
    абсолютных слух сам по себе обычно очень неточный
    
    Как это? «Абсолютный» — это самодостаточное определение точности.
    
    lair
    16.10.2019 17:26
    #20764980
    +1
    Как это? «Абсолютный» — это самодостаточное определение точности.
    Нет. Абсолютный слух — это когда человек слышит высоту звука без предварительной опоры.
    
    Druu
    16.10.2019 17:39
    #20765050
    +2
    Поспорю, у меня есть друзья-абсолютники, которых как раз интервалы и коробят.
    То, что у ваших друзей абсолютный слух, не отменяет того, что интервалы их коробят не из-за него. Абсолютный слух — он абсолютный, абсолютник когда слышит, что "до" — это "до", то слышит это точно так же, как вы, когда слышите букву "а" и понимаете, что это "а". Это один и тот же механизм. Вас может коробить, что кто-то говорит "а" как-то не так, но не может коробить, что "а" находится с "у" в каких-то странных отношениях. Потому что "а" и "у" сами по себе, они никак друг к другу не относятся. Так же и в случае абсолютного слуха — каждая нота интерпретируется сама по себе, т.е. абсолютно, а не друг относительно друга.
    
    Как это? «Абсолютный» — это самодостаточное определение точности.
    Абсолютный — это не про точность, это про способ распознавания.
    Критерием наличия абсолютного слуха считается способность угадывать без относительной привязки полутона равномерно темперированного строя (с привязкой это может делать любой нормальный музыкант). Но темперированный полутон — это, на самом деле, 100 центов. Вы можете, например, разделить этот полутон на 10 частей и потом спросить абсолютника "а этот до-диез — он какой? 0-10? или 60-70? И вам абсолютник не ответит. И если на 5 частей (0-20, 20-40, етц) поделите — тоже, скорее всего, не ответит. Подавляющее большинство абсолютников распознает интервалы максимум в пределах 30 центов, а погрешности темперации ниже. Так что только единичные уникумы среди абсолютников смогут вам при звуке ноты сказать "вот это до в таком-то строю" (естественно, если речь именно об использовании абсолютного слуха, не относительного, относительный на порядок точнее работает). Именно по этой причине, кстати, невозможно хорошо настроить инструмент исключительно на слух, даже если ты абсолютник. Нужна точная базовая нота, с точностью хотя бы центов до 3-5, а это уже на пределе различающих способностей человеческого слуха в принципе. Абсолютники с достаточно точным слухом если и есть, то их 3.5 человека на весь мир не факт что наберется. Почему это так работает? Ну как выше сказано — это тот же механизм распознования букв, он основан на обобщении. Точно так же как ваш мозг обобщает поразному произнесенные "а" (и вы просто слышите "а", не замечая этих малых вариаций) так и абсолютник просто слышит "до", как заучил ее (т.е. как мозг обобщил стимулы).
    
    Ну и кроме того — т.к. способность абсолютного слуха сводится к заучиванию звучания конкретных нот (ну так же как вы заучиваете как звучит "а" или "у"), то то, что вы заучите в детстве — то вы и будете считать "правильной" нотой. И, учитывая что мы живем сейчас во время рт строя, и учат детей на рт пианинках, если вдруг и будет абсолютник с очень точным ас, то он, наоборот, будет нетемперированные ноты (ноты, подчеркиваю, не интервалы) слышать как "неправильные". Т.е. он будет слышать более "правильный" интервал — но с кривыми нотами. И это будет для него весьма печально :)
    
    Абсолютники как раз слышат чистые интервалы.
    Нет, абсолютники не слышат интервалы, т.к. интервал — это отношение звуков. А абсолютники слышат ноты. Абсолютно, вне соотношений с другими нотами. Те ноты, которые выучили в детстве. Вот есть квинта, до-соль или ре-ля — это для относительного слуха одно и то же, один и тот же интервал. Для абсолютного слуха ничего общего между этими квинтами нет. В первом случае одни две ноты, в другом случае — другие. Если вы вдруг встретите не занимавшегося музыкой и не любящего музыку абсолютника, то есть шанс наткнуться на то, что вы просто не сможете ему объяснить, почему и то и то — квинта, он не поймет, что общего между этими интервалами :)
    Бывают у абсолютников проблемы с транспонированием — если транспонируете мелодию, абсолютник может ее не узнать. Хотя интервалы — те же.
    Интервалы — это про относительный слух.
    
    А то, что в темперированной квинте есть биения, слышит любой человек с нормальным слухом, даже не музыкант. Однако, чтобы субъективно воспринимать это как "нестрой", надо весьма сильно упороться :)
    
    grayfolk
    16.10.2019 16:44
    #20764730
    Расшифрую свой ответ.
    Абсолютники как раз слышат чистые интервалы. Их слуху неинтересны проблемы Пифагоровой коммы и ее последствия, решаемые на сегодняшний день равномерной темперацией.
    Они слышат, что в равномерной темперации квинта не строит. Как и остальные интервалы.
    
    lair
    16.10.2019 17:26
    #20764984
    +1
    Вы что-то свое понимаете под абсолютным слухом, не то, чему меня в свое время учили.
    
    grayfolk
    16.10.2019 17:34
    #20765030
    Да, не поспорю )
    Впрочем, не понимаю, в чем тут проблема — слыша чистые звуки абсолютники слышат и интервалы, не так ли?
    Абсолютник слышит до1 — все ок. Слышит соль1 — низит. Или нет?
    
    lair
    16.10.2019 17:40
    #20765056
    +1
    Или нет?
    Совершенно не обязательно, что да.
    
    слыша чистые звуки абсолютники слышат
    А кто вам сказал, что абсолютники слышат "чистые" звуки? У них, как и у других людей, слух имеет зональную природу, и ширина зоны никак не зависит от того, что они абсолютники. Поэтому они слышат "что-то рядом с до" и "что-то рядом с соль", но вот степень этого "рядом" у человека с относительным слухом может быть лучше, чем у абсолютника.
    
    Абсолютник — это только про наличие встроенной точки отсчета. Точность линейки. которую к этой точки отсчета приложили, существует отдельно.
    
    tabmoo
    17.10.2019 10:50
    #20768092
    А Вы не замечали, что абсолютники слышат аккорды «раздельно», что их как бы не заботит то нечто бОльшее, чем является целое звучание аккорда? У меня есть гипотеза, что отличие между абсолютниками и остальными — в степени нелинейности некой части слухового тракта. Грубо говоря, абсолютники слышат мало биений.
    
    lair
    17.10.2019 11:41
    #20768402
    Я в первую очередь слышал от коллег, и, в меньшей степени, замечал сам, что абсолютникам хуже даются созвучия, чем не-абсолютникам. Одна моя знакомая абсолютница говорила мне, что для нее аккорд поначалу "разваливался" на отдельные ноты, и там где не-абсолютник слышал сначала структуру (малый мажорный, например), а потом из нее восстанавливал умом ноты, она слышала ноты (до-ми-соль-ля-диез), а потом восстанавливала структуру (и, как можно видеть в примере, нуждалась в дополнительных заменах).
    
    Druu
    17.10.2019 12:49
    #20769050
    +1
    Я в первую очередь слышал от коллег, и, в меньшей степени, замечал сам, что абсолютникам хуже даются созвучия, чем не-абсолютникам.
    Я как раз об этом говорил выше. Дело тут не в том, что у абсолютников с гармоническим слухом плохо само по себе — дело в том, что они на сальфеджио "сачкуют". Т.е. абсолютнику проще определить аккорд, разложив по нотам (в силу природы абсолютного слуха это делается рефлекторно и практически мгновенно), этим они и занимаются, вместо того, чтобы развивать навык цельного восприятия. Тем более и ребенку трудно объяснить разницу, типа "ты не так аккорд слушаешь". В итоге навык страдает из-за банальной недотренировки — потом уже это обычно в более зрелом возрасте музыканты компенсируют, когда понимают, как и что именно требуется делать.
    
    tabmoo
    17.10.2019 13:00
    #20769118
    -1
    Мой тезис выше как раз в том, что, может, они и не слышат это целое, а вовсе не сачкуют. Абсолютники и не-абсолютники физически слышат по-разному. «Цветной» слух же в каком-то абстрактном смысле совершеннее «серого», поэтому они, возможно, не «компенсируют», а подстраиваются под общую серую массу большинства.
    
    Druu
    17.10.2019 15:14
    #20770062
    Абсолютники и не-абсолютники физически слышат по-разному.
    Нет, одинаково. Абсолютный слух — это в точности та же самая штука, которая распознает у вас буквы и другие подобные звуки. К слову, система распознавания буквы на порядок сложнее, чем система распознавания ноты :)
    Так что все люди на самом деле "абсолютники", просто у кого-то мозг во время критического периода натренировался на распознавание нот (т.е. звуков, необобщаемых по тону, в отличии от букв, которые по тону обобщаются), а у кого-то — нет. Вот и вся разница.
    У китайцев, например, абсолютники — вообще обычное явление, т.к. язык тоновый.
    
    tabmoo
    17.10.2019 15:58
    #20770358
    Возможно, Вы правы, это все надо исследовать. А, может, просто открыть pubmed и найти уже существующие статьи.
    
    Например, ОЧЕНЬ многое понятно в вопросе о происхождении жизни, но никто не удосуживается просто почитать. В научпоп журналах вообще ничего нет с переднего края по этому вопросу, хотя ВСЕ уже написано в статьях. Хоть сам садись пиши дайджест.
    
    Про китайцев непонятно, что Вы имеете в виду. Вы утверждаете, что среди китайцев выше процент абсолютников? Но ведь тоны — это чисто относительное явление. У каждого своя «тоника» в зависимости от высоты голоса, настроения и прочего.
    
    Druu
    17.10.2019 16:58
    #20770696
    -1
    Возможно, Вы правы, это все надо исследовать.
    Все уже давно исследовали.
    
    Про китайцев непонятно, что Вы имеете в виду. Вы утверждаете, что среди китайцев выше процент абсолютников?
    Да. Причем в разы.
    
    Но ведь тоны — это чисто относительное явление.
    Это не важно. На самом деле, ключевое в данном процессе не то, что он работает в абсолютных частотах. Как я уже выше сказал — буквы вы слышите тем самым "абсолютным слухом" (т.е. распознаете их точно так же, как абсолютник распознает ноты), но при этом буква — это как раз своего рода аккорд.
    Тренировка распознавания заключается не в том, чтобы лучше слышать детали, а в том, чтобы не слышать ненужных деталей. Когда вы распознаете звуки речи — ваш мозг учится не учитывать факторы, которые в этих звуках неважны. В тоновых языках высота важна (пусть и относительная) — по-этому мозг носителей тонового языка не учится ее игнорировать, он должен интерпретировать последовательность стимулов, различающихся только тоном, как разные стимулы. Мозг заподноевропейца же наоборот учится воспринимать стимулы, различающиеся тоном, как один и тот же стимул.
    
    toivo61
    18.10.2019 13:14
    #20774956
    Вот где собака порылась :-)
    Подтверждаю. Жена — скрипачка абсолютница, с 18 летним академическим стажем. Гитару настраивает без тюнера.
    Но Ля-минор от Ми-мажора на гитаре не отличает — нижняя нота то МИ. С клавишами проблем нет.
    
    lair
    18.10.2019 13:32
    #20775066
    Гитару настраивает без тюнера.
    Мне вот в таких случаях как раз очень интересно, какой строй получается — чистый или темперированный, и если темперированный, то как. Потому что струнные скрипичного семейства регулярно настраивают либо по чистым, либо по темперированным квинтам в зависимости от других инструментов.
    
    toivo61
    18.10.2019 14:13
    #20775316
    Не могу сказать — точности ушей не хватает.
    Обычно она просто настраивает открытые струны, после чего уже можно песняки у костра поорать :)
    Причем, если ей лень настраивать скрипку как положено, или она не сильно расстроена, то она на лету пальцами «питчит» каждую ноту.
    На пентатонику и микротонику ругается: «Вам, что семи нот не хватает?.. А если надо, то можно и пальцем подтянуть куда надо!» Как-то так.
    
    tabmoo
    18.10.2019 14:34
    #20775448
    В интернете можно найти материал на тему настройки гитары без тюнера, в которой доказывается (хотя это и так очевидно), что самые популярные методы (5-й лад второй струны и т. д.) не дают темперации. Далее предлагается улучшенный метод настройки (через 7-е лады, вроде).
  1. Dr_Faksov
    17.10.2019 06:56
    #20767212
    Читал тоже. Вроде как жаловался что ему октавы мало и нотный строй жмёт.
1. grayfolk
  16.10.2019 17:44
  #20765088
  +1
  Druu lair
  Спасибо за разъяснения. Сам, как человек, которого почему-то всегда многие считали абсолютником (хотя у меня типичный относительный слух, а абсолютно слышать периодически может любой человек с тренированным слухом), никогда не задумывался о каких-то там нюансах. Ну, слышу — и все )
1. A1054
  16.10.2019 21:04
  #20766054
  если 19 хватит, а то иногда говорят, что нужно 85, и тогда все ОК: )

acidhouse
16.10.2019 16:09
#20764520
Фиксированный звукоряд нужен пальцам. Мозгу он не нужен. Мозг слышит интервалы.
Консонанс привлекает внимание, потому что консонантные звуки в природе скорее всего имеют один и тот же физический источник. Например, чей-то рот с гласными. Консонанс не случаен. При этом ухо довольно толерантно к небольшим расстройствам этого самого консонанса. Тоже понятно, почему — тренировать слух обезьяне негде, и отличить чистую квинту от не очень чистой, чтобы понять, это звук такой, или тебя приглючило, скорее всего не очень нужно.
Со средних веков многие пытались аппроксимировать степень консонанса и это удается на удивление хорошо простыми формулами.
Например, BenedettiHeight(a/b)=a*b (где a/b — сокращенная дробь) — это 16-й век.
Какой бы способ аппроксимации консонанса не использовался, будет получаться примерно один и тот же список интервалов: 2:1 3:2 4:3 5:3 5:4 7:4 6:5 7:5 8:5 7:6 8:7 11:6 9:7 10:7 9:8, и так далее.
Т.е. октава, квинта, кварта…
Интервалы из списка распознаются ухом четко, у них свой характер, и их сложно перепутать, а близкие интервалы с более сложными дробями скорее будут рассматриваться как ошибочная версия правильных интервалов. Чем дальше по списку — тем все менее внятные интервалы. Нет, можно натренировать слух различать их, но посыл-то в чем. Посыл мозг не распознает. Четвертьтон сам по себе посыла не несет.
Так у нас возникает задача: как получить максимум интересных для нас интервалов, не решая сложные оптимизационные задачи в уме, когда мы поем, либо дергаем струну.
Ответ — фиксированный звукоряд. Если у нас есть N нот, у нас будет N*(N-1) пар нот. Далее мы хотим, чтобы вероятность того, что взяв две случайные ноты, мы получим распознаваемый интервал была высокой, желательно, чтобы все такие пары были максимально консонантными (мы же древние люди и джаз нам не нужен). Можно решить эту задачу перебором, можно подключить теорию чисел.
Если решить эту для 5 нот, получится пентатоника. Любая пара нот пентатоники весьма консонантны, а ближайшие пятинотные альтернативы звучат весьма плохо.
Если решить ее для 7 нот, будет сложнее, потому что сделать все пары нот консонансами, когда у тебя семь нот, нельзя. Нужен будет полутон. Но можно минимизировать их число, и получится диатоника — 7 нот в каком-то из порядков, типа минора, или мажора.
Дальше возникает проблема того, что какие-то пары нот все равно сильно расстроены. И у нее есть два пути решения.
Первый — добавлять какие-то дополнительные ноты для частных случаев. Это путь многих незападных музык.
Второй — расстраивать существующие ноты, чтобы плоховатые интервалы размазались ровным слоем. Это западный путь.
И вот на этом этапе появляется число 12, которое настолько хорошо аппроксимирует диатонику (т.е. фиксированный звукоряд из 7 нот с максимумом пар консонансов), что является хорошим компромиссов.
Проблема в том, что несколько хороших консонансов выпадает совсем. Например, 7:4. Шикарный интервал. Но вот запихнуть его в фиксированный звукоряд так, чтобы из него что-то не выпало при этом — тяжело.
В диатонике все хорошо, какую пару нот не нажми, все равно будет относительно консонантный звук. А вот 7:4 все поломает. Отсюда и возникает эта пропасть между привычной музыкой и микротонами. Экзотические и при этом приятно звучащие интервалы (которых не очень много на самом деле) просто не влезают в фиксированные ряды, они их ломают и при нажатии клавиши возникает известный эффект расстроенного пианино.
1. zuborg
  16.10.2019 17:58
  #20765188
  Ряд из 19 нот дает чуть лучшие приближения консонансов, чем из 12:
  
  1.037 = 2^(1/19)
  1.076 = 2^(2/19)
  1.116 = 2^(3/19)
  1.157 = 2^(4/19) ~ 7:6 = 1.167 ~ 8:7 = 1.143
  1.200 = 2^(5/19) = 6:5 = 1.200
  1.245 = 2^(6/19) ~ 5:4 = 1.250
  1.291 = 2^(7/19) ~ 9:7 = 1.286
  1.339 = 2^(8/19) ~ 4:3 = 1.333
  1.389 = 2^(9/19) ~ 7:5 = 1.400
  1.440 = 2^(10/19) ~ 10:7 = 1.423
  1.494 = 2^(11/19) ~ 3:2 = 1.500
  1.549 = 2^(12/19) ~ 11:7 = 1.571
  1.607 = 2^(13/19) ~ 8:5 = 1.600
  1.667 = 2^(14/19) = 5:3 = 1.667
  1.728 = 2^(15/19) ~ 12:7 = 1.714 ~ 7:4 = 1.750
  1.793 = 2^(16/19) ~ 9:5 = 1.800
  1.859 = 2^(17/19) ~ 13:7 = 1.857 ~ 11:6 = 1.833
  1.928 = 2^(18/19)
  
  Соотношения частот для 12-ти нотного ряда выглядят так:
  1.059 = 2^(1/12)
  1.122 = 2^(2/12)
  1.189 = 2^(3/12)
  1.260 = 2^(4/12)
  1.335 = 2^(5/12)
  1.414 = 2^(6/12)
  1.498 = 2^(7/12)
  1.587 = 2^(8/12)
  1.682 = 2^(9/12)
  1.782 = 2^(10/12)
  1.888 = 2^(11/12)

A1054
16.10.2019 20:59
#20766032
Мне кажется, вы не совсем правы. Хотя в этой области много точек зрения, т.к. идеального решения нет.
Аксиомы, чтобы получился современный строй, КМК, такие:
1. Равномерность, чтобы обеспечить транспорт мелодий и легкую настройку инструментов при смене тональности. Иначе для каждой тональности пришлось бы перестраивать инструменты. Или делать очень много разных тонов (под сотенку) для одной октавы.
2. Простота.

Собственно, пп. 1 и 2 оказались решающими. «Технологический» подход победил, а сторонники чистых тонов проиграли.
3. Т.к. В равномерном строе все интервалы звучат не чисто, нужно принять субъективное волевое решение, для каких интервалов минимизируем ошибку, а для каких допускаем чуть большее расхождение с чистым тоном. Самой важной показалась квинта, наиболее консонансный интервал после октавы.

В результате при делении октавы на 12 частей получилась простая система, в которой квинта (и кварта тоже, вы правы) очень близки к чистым интервалам. Терция звучит уже хуже, но, как я понимаю, ее принесли в жертву простоте.
В чем мне видится у вас неточности:
1. Вы оптимизируете звучание интервала квинта — кварта, т.е. большой секунды. Почему? Это не очевидно. Задача состоит в том, чтобы разделить октаву на равные доли, чтобы значения всех основных интервалов были максимально близки к чистым. Но минимизировать нужно не сумму квадратов отклонений, а субъективно воспринимаемую важность интервалов. Скорее всего, это квинта --> кварта --> терция (?).
2. Вы забыли про простоту. В вашем же примере 7/41 ближе к секунде, чем 2/12. И к квинте, кстати, тоже: ) Наверное, выбор произошел из-за относительной простоты и «технологичности» разбиения октавы на 12 тонов.
3. Ну и замечание в целом. В музыкальных строях много субъективного. Мы воспитаны на равномерно темперированной музыке, и нам все кажется ОК. Но, боюсь, у средневекового музыканта, привыкшего к чистым тонам, от наших терций волосы стали бы дыбом. Тут ведь как — меняешь систему, меняется все, в том числе и композиции. Они либо заточены под определенную тональность, либо некоторые интервалы звучат не чисто (а композиторы это учитывают). Мы немного пожертвовали чистотой ради «технологичности». Но это не математический, а субъективный выбор.

Refridgerator
17.10.2019 10:41
#20768054
Кстати говоря, в современной музыке нот не 12, а больше. До диез не равно ре бемолю.
1. math_coder
  17.10.2019 10:52
  #20768098
  До диез не равно ре бемолю.
  Как такое может быть?
  1. Refridgerator
    17.10.2019 10:57
    #20768112
    Так же, как и в математике предел слева может быть не равным пределу справа.
    
    math_coder
    17.10.2019 11:30
    #20768312
    Если это аналогия, то она решительно непонятна.
    
    Druu
    17.10.2019 11:34
    #20768340
    +1
    Разница между до и до-диезом/до-бемолем равна полутону только в равномерно темперированных строях. А если бемоль и диез не совпадают с полутоном, то они не совпадают и друг с другом.
    
    math_coder
    17.10.2019 12:22
    #20768784
    А, теперь немного понятно, спасибо. Но я бы сформулировал это иначе: разница между до и до-диезом/до-бемолем равна полутону всегда, за исключением только строев, не являющихся равномерно темперированными.
    
    lair
    17.10.2019 12:38
    #20768954
    Но я бы сформулировал это иначе: разница между до и до-диезом/до-бемолем равна полутону всегда, за исключением только строев, не являющихся равномерно темперированными.
    Когда исключений больше, чем нормы, возникает вопрос, что же норма.
    
    tabmoo
    17.10.2019 12:46
    #20769030
    Да, поэтому формулировку выше надо заменить на «противоположную».
    
    Все о чем тут спор идет, это описание попытки впихнуть невпих..., эээ живые интонации пения и смычковых (в основном) в прокрустово ложе темперации в целях клавишных, ладовых и т. п. инструментов. Неизбежное зло, да, но нельзя забывать, что первично.
    
    Это так же как тут появляются статейки айтишников на музыкальные темы, где под «музыкой» может пониматься бог знает что, в основном, всяческий акустический мусор.
    
    Refridgerator
    17.10.2019 12:40
    #20768962
    +1
    В теории музыки до-диез не равен ре-бемолю по определению, иначе для них не вводились бы отдельные обозначения, а была бы самостоятельная нота с независимым названием. То, что в 12-ступенном равномерном строе им соответствует одна и та же частота — это свойство строя, а не музыки.
    
    Refridgerator
    17.10.2019 12:57
    #20769100
    +1
    Теория музыки не оперирует полутонами, она оперирует ступенями и интервалами. Мелодия — это не последовательность нот, мелодия — это последовательность интервалов.
    
    tabmoo
    17.10.2019 11:41
    #20768394
    Классная у вас дискуссия.
    
    А в несовременной что? Строго 12? ))
    
    Как такое может быть? Может стоит учебник гармонии почитать?
    
    Продолжаю наблюдение. ))
    
    lair
    17.10.2019 11:43
    #20768414
    Ну, автор статьи нам пытается доказать, что строго 12, да, и это объективный закон.

Число, лежащее в основе современной музыки +55

Почему двенадцать?

Постановка задачи

Что такое гармония?

Условие первое. Тоника, кварта, квинта, октава

Условие второе. Инвариантность

Расчет

Заключение. Число, лежащее в основе

Комментарии (301)

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор

nihole Автор