16.06.2020 22:16
nihole 26 3400 Источник

О чем эта статья


Здесь будет описан метод анализа логических цепочек. Изначально созданный как инструмент ведения дискуссий, этот подход может быть полезен в любой ситуации, где нужно найти ответ на вопрос истинно утверждение или ложно. В качестве интересного следствия приведенный анализ позволяет найти ключевые утверждения, лежащие в основе сформировавшейся картины мира. Также будет сформулирована аксиома волнового анализа о фундаментальном ограничении аналитического подхода.


image


Есть ли смысл в спорах


Какое-то время назад, я, как и многие другие обычные и до этого даже аполитичные люди, оказался добровольцем в информационной войне. Немалое количество часов провел я в спорах, доказывая свою правоту и удивляясь "тупости" противоположной стороны. Потихоньку нешуточные страсти поутихли, не причинив существенного ущерба. Не смотря на противоположность взглядов и подчас высокий накал дискуссии, я и мои оппоненты сумели не выйти за рамки разумности и сохранить хорошие отношения. В конце всего этого мы приобрели что-то вроде иммунитета к политическим спорам, и это, конечно, важно, но, как мне кажется, есть еще одно приобретение, и более ценное приобретение.


Думаю, что многие это проходили. Когда количество споров на одну и ту же тему с разными людьми переваливает за десяток, спорить становится уже неинтересно. Вы понимаете, что знаете и предсказываете их логические цепочки, аргументы и контраргументы. Конечно, иногда встречаются новые ходы, но все же "основные логические магистрали" остаются приблизительно теми же, и их количество вполне ограничено. И это в принципе можно рассматривать как приобретение. Фактически таким образом разрабатывается некая карта логических связей. Правда, эта карта разбита на многие осколки, которые хранятся лишь в умах большого количества людей, не формализованная, не выраженная, с ложными или тупиковыми тропками…


В какой-то момент для некоторых тем мне захотелось запротоколировать и проанализировать эту карту. Работая над этим, я получил то, что я назвал волновым анализом и несколько, на мой взгляд, интересных выводов, которыми и хочу поделиться.


Терминология, используемая в статье

Здесь краткое описание терминов, вводимых и поясняемых в статье.


  • Волновой анализ — метод нахождения ответа на вопрос, является ли утверждение истинным или ложным с использованием логических цепочек, основанных на операциях опровержения и дополнения (см. ниже).
  • Волновой граф. Логические цепочки волнового анализа могут быть представлены в виде графа. Вершины графа — это утверждения. Ребра графа — это связи между утверждениями. Существует 3 основных вида связи между вершинами волнового графа:
    • прямое опровержение
    • косвенное опровержение
    • дополнение
      все остальные связи, необходимые в волновом анализе, могут быть представлены через эти три.
  • Корневое утверждение (корневая вершина) — анализируемое основное утверждение, является корнем волнового графа. В рамках описанного подхода мы ожидаем, что это утверждение может быть только строго истинным или строго ложным.
  • Прямое опровержение. Предположим у нас есть два утверждения A и B. Если истинность утверждения B приводит к тому, что утверждение A ложно, то это называется прямым опровержением и обозначается как A --п-> B. Символ --п-> значит "ложно потому, что". На графе прямое опровержение обозначается как сплошная линия со стрелкой от A к B.
  • Косвенное опровержение. Отличается от прямого лишь силой связи. Если в случае прямого опровержения истинность B однозначно приводит к ложности A, то в случае косвенного опровержения истинность B лишь увеличивает вероятность истинности A. Обозначается как A --к-> B. Символ --к-> значит "с некоторой вероятностью ложно потому, что". На графе обозначается как пунктирная линия со стрелкой от A к B.
  • Дополнение (или отрицание). Это обычное логическое отрицание, то есть если B истинно, то A ложно и, наоборот, если B ложно, то A истинно. Будем обозначать это как A<->B. Легко показать, что если A<->B, то B<->A. На графике будем обозначать это сплошной линией с двумя разнонаправленными стрелками.
  • Прямое подтверждение. Если B истинно, то А тоже истинно. Легко увидеть, что это может быть представлено как A<->C--п->B. (C — просто дополнение А, и может быть выражено как "не А").
  • Косвенное подтверждение. Если B истинно, то вероятность того, что А тоже истинно увеличивается. Легко увидеть, что это может быть представлено в виде A<->C--к->B.
  • Волновые логические цепочки (волны). Если следовать стрелкам волнового графа, то мы получим "волну" утверждений, последовательно опровергающих предыдущее в цепочке утверждение и, соответственно, поочередно опровергая и подтверждая корневое утверждение.
  • Сходимость (разрешимость) волнового графа. Считается, что волновой граф сходится (или является разрешимым), если его анализ приводит к однозначному выводу о ложности или истинности корневого утверждения.
  • Тупиковые вершины. Это утверждения, которые не опровергаются ни одним другим утверждением. На графе из таких вершин не исходит ни одной стрелки (в том числе и двунаправленных).
  • Циклы. Это любые циклы в волновых логических цепочках. Самые простые и фундаментальные циклы — это циклы, состоящие из двух элементов: дополнение и взаимное опровержение. Наличие неразрешимых циклов является следствием скрытой информации.
  • Опорные точки. Это минимальный набор самосогласованных утверждений (в идеале одно), в которые человек верит, что позволяет графу сойтись. В зависимости от того, с каким знаком эта вера (верит ли он, что эти/это утверждение истинно или ложно) граф сходится либо с положительным, либо с отрицательным результатом. На полном волновом графе (см. определение ниже) эти вершины являются частью неразрешимых циклов (скрытая информация).
  • Причинный анализ. Анализ основанный на причинно-следственных связях.
  • Причинный граф. Этот граф можно получить из волнового, если следовать по волновым логическим цепочкам от опорного утверждения в сторону корневого, но только по утверждениям, находящимся в той же фазе, что и опорное.
  • Абсолютно полный волновой граф. Волновой граф, учитывающий все волновые зависимости. Этот граф скорее теоретический, потому что на практике нет необходимости рассматривать все "волны".
  • Полный волновой граф. Волновой граф, включающий все волновые логические цепочки с "разумной" (соответствующей контексту дискуссии) степенью глубины анализа.
  • Основная аксиома волнового анализа: "всегда есть скрытая информация, не позволяющая однозначно разрешить полный волной граф".

Волновой анализ


Связи между утверждениями


Рассмотрим два утверждения: A и B. Будем считать, что каждое из этих утверждений может быть или истинным или ложным. Тогда возможны следующие зависимости утверждения A от B:


  • Независимость (А не зависит от В). Истинность или ложность утверждения A никак не зависит от истинности или ложности утверждения B.

  • Прямое опровержение. Если утверждение B истинно, то утверждение A ложно. Будем обозначать такую связь, как A --п-> B. Суть в том, что стрелка --п-> фактически заменяет выражение "ложно потому, что", то есть A --п-> B это краткая запись выражения "A ложно потому, что B (истинно)". На графе эту связь мы будем обозначать сплошной линией со стрелкой от А к B:


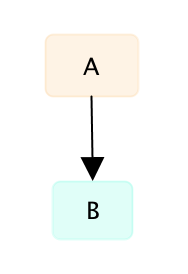
    Прямое опровержение
    Замечание

    При этом, если утверждение B ложно, то это может ничего или почти ничего не значить для А.

    Пример

    Утверждение А: "Вчера в 7 часов вечера Алиса была дома".
    Утверждение B: "Вчера в 7 часов вечера Алиса была в театре".
    A --п->B: "Вчера в семь часов вечера Алиса не была дома, потому что она была в театре."

  • Дополнение (логическое отрицание). Если утверждение B истинно, то утверждение A ложно, и если утверждение B ложно, то утверждение A истинно. Будем обозначать это как А <-> B. Легко показать, что если А <-> B, то B <-> A. На графе эту связь мы будем обозначать сплошной линией с двунаправленной стрелкой:
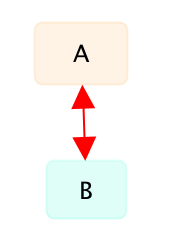
    Дополнение
    Пример

    Утверждение А: "Вчера в 7 часов вечера Алиса была дома".
    Утверждение B: "Вчера в 7 часов вечера Алисы НЕ было дома".
  • Прямое подтверждение. Если утверждение B истинно, то утверждение А тоже истинно. Будем называть это прямым подтверждением. Легко показать, что такая зависимость составляется из предыдущих зависимостей: A<->C--п-> B. В этом случае если B истинно, то C ложно, а значит A истинно. На графе это может быть представлено в виде
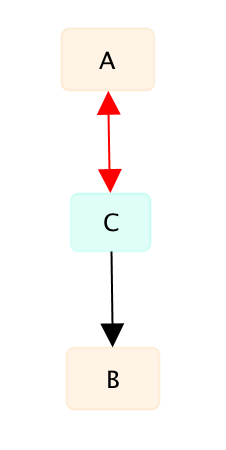
    Прямое подтверждение
    Пример

    Утверждение А: "Вчера в 7 часов вечера Алиса была дома".
    Утверждение B: "Вчера в 7 часов вечера Боб был в гостях у Алисы, и видел её дома".
    A <->C--п->B: "Вчера в семь часов вечера Алиса была дома, потому что Боб в это время был у нее в гостях и видел её там."
    Дословно же эту запись можно представить, как "Вчера в семь часов вечера Алиса не была вне дома, потому что Боб был у нее в гостях и видел её дома".

  • Косвенное опровержение. Если утверждение B истинно, то вероятность того, что утверждение А ложно увеличивается. Будем называть это косвенным опровержением и обозначать как A --к-> B. На графе будем обозначать это пунктирной линией со стрелкой от A к B:


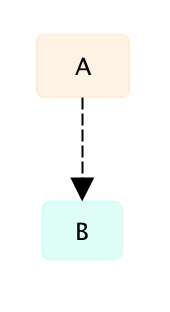
    Косвенное опровержение
    Замечание

    При этом, если утверждение B ложно, то это может ничего не значить для А.
    Отличие от прямого опровержения — в силе связи. Если В истинно, то это еще не значит, что А ложно, но говорит нам о том, что вероятность того, что А ложно увеличивается.

    Пример

    Утверждение А: Вчера в 7 часов вечера Алиса была дома".
    Утверждение B: "Вчера в 7 вечера к Алисе приходил Боб, звонил в дверь, но никто не открыл".
    A --п->B: "Вчера в семь часов вечера Алисы скорее всего не было дома, потому что в это время приходил Боб и звонил в дверь, но никто не открыл". Но в действительности Алиса могла быть дома, но по каким-либо причинам не могла или не хотела открывать.

  • Косвенное подтверждение. Если утверждение B истинно, то вероятность того, что утверждение А тоже истинно увеличивается. Будем называть это косвенным подтверждением. Легко показать, что такая зависимость составляется из предыдущих зависимостей: A<->C--к-> B. В этом случае, если B истинно, то вероятность того, что C ложно увеличивается, а значит вероятность того, что A истинно тоже увеличивается. Отличие от прямого подтверждения опять-таки в силе связи (как и для косвенного опровержения). На графе это может быть представлено как
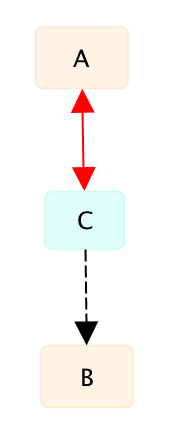
    Косвенное подтверждение
    Пример

    Утверждение А: "Вчера в 7 часов вечера Алиса была дома".
    Утверждение B: "Вчера в 7 часов вечера соседи слышали звуки пианино из квартиры Алисы".
    A <-> C --к->B: "Вчера в семь часов вечера Алиса скорее всего была дома, потому что соседи слышали звуки пианино из ее квартиры". Но, в действительности, это ведь могла быть просто запись.

Таким образом мы ввели 3 основных вида зависимости утверждения A от утверждения B:


  • прямое опровержение
  • косвенное опровержение
  • дополнение (логическое отрицание)

Все остальные необходимые для анализа комбинации можно получить из этих 3х.


  • в случае нескольких опровержений одного утверждения, они объединяются логическим "или". На данном графе показано, что N ложно потому что M1 или M2 или… Mk (истинно)


    опровержение
    Замечание

    Возможна комбинация прямых и косвенных опровержений.

  • если мы хотим показать аргументы, поддерживающие наше утверждение, то, как уже было замечено выше, это можно сделать через опровержение дополнения. Так, например, если мы имеем утверждение N1 и аргументы M1, M2, .., Mk, где M1 — косвенное подтверждение, а M2 и Mk — прямые, то это будет выглядеть следующим образом



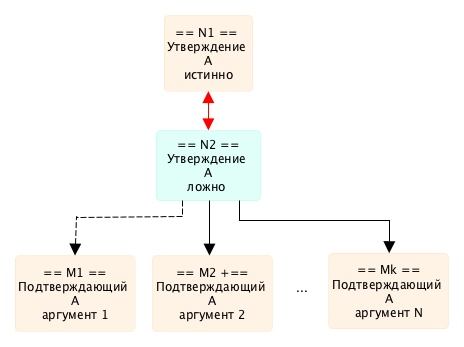
Отелло

Граф, построенный по этим правилам мы будем называть волновым графом.


Волновой граф


Предположим, что происходит обсуждение истинности/ложности утверждения A. Утверждение А должно быть сформулировано таким образом, что возможен один и только один вариант — А истинно или А ложно.


Построим волновые логические цепочки в виде графа по следующему принципу:


  • утверждение А будет корнем нашего графа
  • вершинами графа являются утверждения, поддерживающие или опровергающие корневое утверждение. Для удобства мы будем нумеровать вершины
    Замечание

    В данной статье мы будем использовать положительные числа, если утверждение является подтверждающим наше корневое утверждение, и отрицательные числа — если опровергает, но это, конечно, необязательно (обязательным является однозначность нумерации). При этом номером +0 будет обозначена корневая вершина, а -0 — её дополнение. Конечно, это всего лишь обозначение, поэтому тот факт, что +0 = -0 ничему не мешает.
  • ребра графа отражают перечисленные виды зависимости и, соответственно, у нас всего лишь 3 вида ребер

Волновой логической цепочкой (волной) мы будем называть движение от вершины к вершине по стрелкам ребер. Очевидно, что в такой цепочке мы всегда будем иметь последовательность аргументов за и против, что лично мне напоминает волну. Приблизительно это мы наблюдаем и в "правильном" споре (что, к сожалению, бывает далеко не всегда).


Пример волнового графа. Отелло

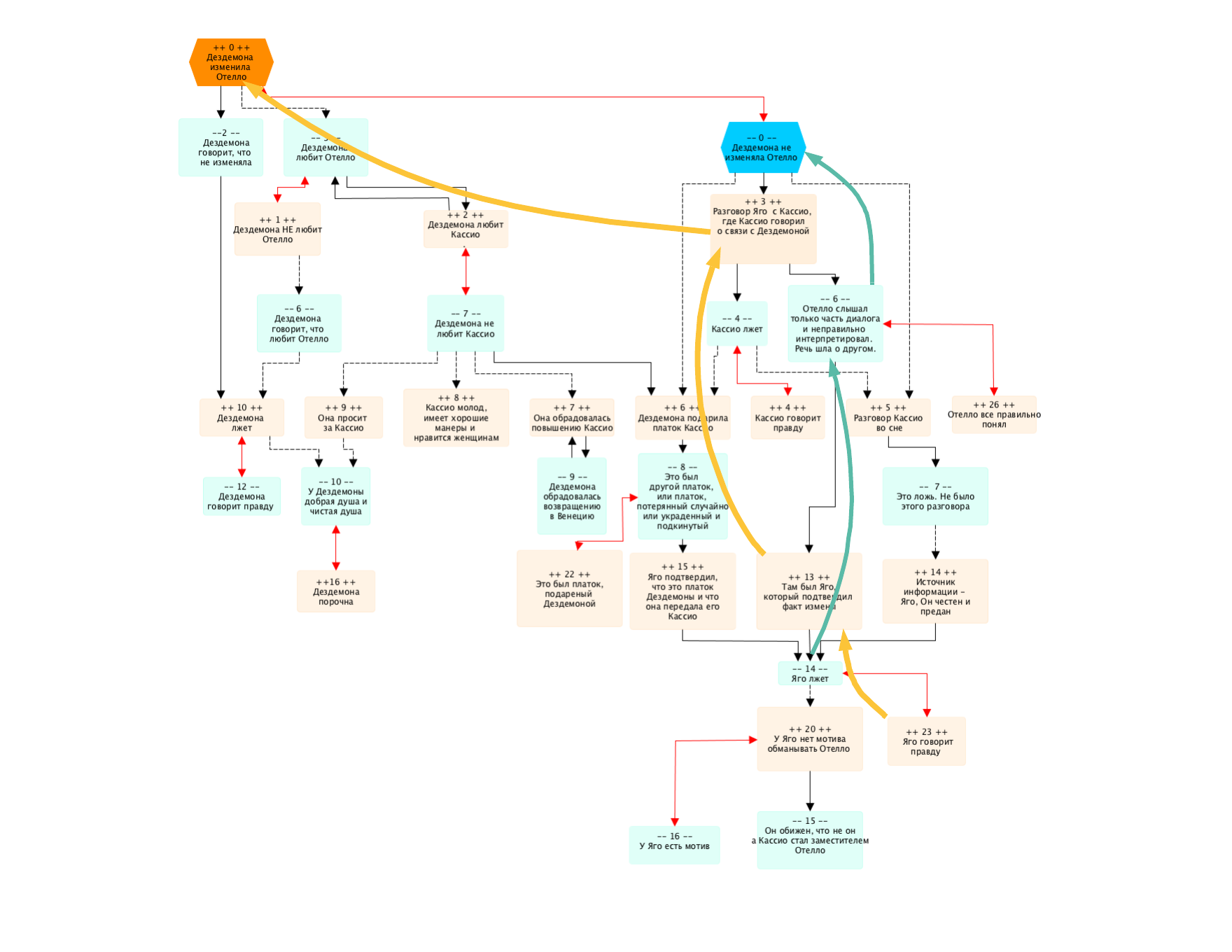
В качестве иллюстрации волнового анализа попробуем помочь Отелло разобраться в том, изменяла ли ему Дездемона. Вот приблизительно так может выглядеть волновой граф:



  • корнем этого графа является утверждение "Дездемона изменила Отелло"
  • далее вниз мы можем наблюдать волновые логические цепочки (волны). Цвет ближе к голубому (мы будем называть его голубым) является подтверждением того, что "Дездемона НЕ изменяла Отелло", а цвет ближе к желтому (мы будем называть его желтым), является подтверждением противоположного, а именно, что "Дездемона изменила Отелло". Мы видим чередование голубых и желтых вершин
  • мы знаем, что истинными являются все голубые утверждения, Отелло же на момент убийства был уверен в том, что истинными являются все "желтые утверждения"
  • рассмотрим примеры всех возможных зависимостей:
    • прямое опровержение
      +0 --п-> -2: утверждение, что "Дездемона изменила Отелло" ложно потому, что "Дездемона говорит, что она не изменяла". Если то, что говорит Дездемона правда, то, конечно же, это прямое опровержение того, что Дездемона изменила
    • косвенное опровержение
      +0 --к-> -3: утверждение, что "Дездемона изменяла Отелло" ложно потому, что "Дездемона любит Отелло". Действительно, если она действительно любит Отелло, то это еще не значит, что она ему не изменяла, но этот факт увеличивает вероятность того, что Дездемона верна Отелло
    • дополнение
      +0 <-> -0: "Дездемона изменила Отелло" и "Дездемона не изменяла Отелло".
    • прямое подтверждение
      +0 <-> -0 --п-> +3: "Дездемона изменила Отелло" потому, что "Кассио сам рассказал об этом". Очевидно, что, если Кассио рассказал правду, то это прямое подтверждение
    • косвенное подтверждение.
      +0 <-> -0 --к-> +5: "Дездемона изменила Отелло" потому, что "Кассио говорил о связи с Дездемоной во сне". Понятно, что даже если это и правда, и Кассио говорил об этом во сне, то это еще не значит, что Дездемона изменила. Однако, это все же увеличивает вероятность этого
  • мы можем рассмотреть отдельные волновые логические цепочки (волны). Для этого нужно просто следовать стрелкам. Помним, что каждая однонаправленная стрелка от вершины N к вершине M значит, что "N ложно потому, что M (истинно)". Так же у нас может быть конструкция с подтверждением (описана выше). Например, рассмотрим логическую цепочку +0 <->-0 —п-> +3 —п-> -6 —п-> +13 —п-> -14 —к-> +20 —п-> -15 <-> + 21 --к-> -19 <->+25:
    • +0 <->-0 —п-> +3: Дездемона изменила Отелло, и доказательством является то, что Отелло слышал разговор Кассио с Яго, где Кассио говорил о связи с Дездемоной
    • +3 —п-> -6: но это не так, потому что Отелло слышал только часть разговора и неправильно интерпретировал его
    • -6 —п-> +13: интерпретация верна, Яго подтвердил верность интерпретации
    • +13 —п-> -14: Яго лжёт
    • -14 —к-> +20: У Яго нет мотива обманывать Отелло
    • +20 —п-> -15: Нет, у Яго есть мотив. Он обижен на то, что Отелло назначил не его заместителем, а Кассио
    • -15 <-> + 21 --к->-19: Яго обижен на Отелло и держит на него зло потому, что он злой и порочный человек
    • -19 <->+25: Это не так, потому что Яго хороший и честный человек
      Зачем мы закончили --19 <-> + 25? Потому, что мы не можем точно знать (Отелло не может), каким человеком является Яго, злым или хорошим. У нас нет аргументов. Такая же ситуация бывает и в споре, когда оппоненты просто упираются в "да — нет" без какой-либо аргументации. Это и есть одна из опорных точек.
      Замечание

      Оценочные утверждения хорошо/плохо в действительности сложно анализировать. Проще говорить о фактах. Но часто подобное восприятие может быть ключевым для принятия решения (см. опорные точки ниже)

Анализ волнового графа


Сходимость графа


Будем называть граф разрешимым (или сходящимся), если анализ данного графа однозначно приводит к выводу о том, истинно или ложно корневое утверждение.


Будем называть вершину N тупиковой, если из нее не выходит ни одной стрелки, в том числе и двунаправленной (дополнение), то есть она не опровергается ни одним утверждением (в идеале ни прямым, ни косвенным, но существенными для анализа являются только прямые опровержения).


Тогда утверждение M, для которого M --п-> N будем называть утверждением, опровергнутым N.


Ниже приведен алгоритм разрешения волнового графа.


  • найдем (если есть) тупиковую вершину N
  • найдем все утверждения, опровергнутые N. Пометим эти вершины и тупиковую вершину N как "удаленные". Все стрелки, ведущие к ним и от них, также пометим как "удаленные". Мы не учитываем их в дальнейшем анализе
  • все вершины, которые не входят в волновые логические цепочки с началом в корне (потеряна логическая связь с корневым утверждением) помечаем как "удаленные". Все стрелки, ведущие к ним и от них, также пометим как "удаленные". Мы не учитываем их в дальнейшем анализе.
  • если для двух вершин N и M таких что N<->M вершина M помечена как удаленная, то вершина N становится тупиковой (доказанной), и все стрелки ведущие из нее (все опровержения) помечаются как удаленные
  • повторяем этот процесс до тех пор, пока не кончатся тупиковые вершины
  • когда тупиковые вершины закончатся у нас возможны 3 варианта:
    • корневое утверждение будет помечено как "удаленное". Тогда данный граф считается решенным. Наше корневое утверждение оказалось ложным
    • осталось только корневое утверждение. В этом случает данный граф считается решенным. Наше корневое утверждение оказалось истинным
    • все остальные варианты. В этом случае мы можем утверждать, что существует скрытая информация, которая не позволяет нам определить, является утверждение ложным или истинным
      Замечание

      Теоретически, в зависимости от последовательности взятия тупиковых вершин, мы можем получить разный результат. Это говорит или об ошибке в логике, или о ложной информации, принятой за истину. Если наш алгоритм в зависимости от последовательности действий приводит к разным результатам, то мы должны сначала исправить ложную информацию или ошибку в логике.

Вернемся к примеру с Отелло.


Пример сходимости. Дездемона виновна

Мы видим, что в том виде, как представлен волновой граф, он неразрешим. У нас только 5 тупиковых вершин: +19, +18, +17, +11 и +8. Вершины +8, +18 и +19 отражают косвенные связи, поэтому не интересны. Но утверждение +17 ("Дездемона умеет лгать, потому что она уже лгала отцу, когда убежала к Отелло") является действительно тупиковым. Это приводит к тому, что вершины +17 и -11 в соответствии с нашим алгоритмом мы помечаем как удаленные. Также вершину +11 разумно признать тупиковой. Нельзя полагаться на показания Эмилии о том, изменяла ли Дездемона. Она принципиально не может знать правды. Может предполагать, догадываться, но она не знает. Поэтому вершины +11, -1 можно удалить.


Но все это мало помогает нам продвинуться в разрешении данного графа.


Так почему же восприятие Отелло сложилось таким образом, что он был уверен, что Дездемона виновна?


Давайте посмотрим, что произойдет, если вершину +23 ("Яго говорит правду") или +25 ("Яго хороший и честный человек") считать истинной? Как только мы принимаем это, то


  • вершина +23 (или +25) становится тупиковой (нет опровержений)
  • это приводит к тому, что ее и вершину -14 (со всеми связями) мы помечаем как удаленные
  • вся ветка с вершинами +20, -16, -15, +21, +25, -19 теряется связь с корнем и поэтому также удаляется со всеми связями
  • далее, вершины +15, +14, +13 становятся тупиковыми
  • таким образом, удаляются они (+15, +14, +13), а также те вершины, которые были опровергнуты ими, а именно, -8, -7, -6 и те вершины, которые потеряли "связь" c корневым утверждением: +22, +26
  • теперь тупиковой вершиной является вершина +6. Важная вершина, потому что она говорит о том, что Дездемона подарила платок Кассио. Это приводит к тому, что эта вершина, а также вершины -7, +7, +8, +9 вместе со связями могут быть удалены из графа
  • тогда вершина +2 становится тупиковой, что позволяет нам удалить вершины +2, -3, +1, -5, -26

  • следующим шагом мы можем удалить ветку, которая потеряла связь с вершиной: +12, -13, +19, +18, и мы получаем следующий граф:




И этот граф формально опять-таки является неразрешимым. Причина в циклах:


  • -4 <-> +4: Кассио лжёт или говорит правду? Отелло не знает ответа. Да, он слышал разговор, да, "честный Яго" подтвердил, что он не ослышался и правильно понял суть, но, возможно, Кассио просто бахвалился
  • -10 <-> +16: Дездемона порочна или добрая и чистая душе? Это та дилемма, которую Отелло и пытается решить. Но этот цикл не так уж важен, потому что вершина -10 является лишь косвенным опровержением вершины +10
  • +10 <-> -12: Дездемона лжет или говорит правду?

В данном месте анализа Отелло уже сделал вывод, что Дездемона любит Кассио, но факт измены пока не подтвержден. Возможно, Кассио говорит неправду. Но характер мавра не знает полутонов, поэтому ему проще принять факт измены. Он делает еще один шаг, поверив, что Дездемона обманывает его, и что Кассио действительно рассказывал о своей связи с Дездемоной. Теперь граф сходится.


Этот анализ показывает, что, как только Отелло принимает, что Яго говорит правду, и это перевешивает его доверие Дездемоне (соответственно, перестает ей доверять), так сразу граф формально сходится.


Пример сходимости. Дездемона невинна

Итак, Отелло убил Дездемону в полной уверенности в ее порочности. Но сразу после ее смерти его видение ситуации развернулось на противоположное. Что же произошло, и как это объясняет волновой анализ?


Вспомним последний акт. Эмилия, под впечатлением от смерти Дездемоны разоблачает своего мужа Яго, объясняя мавру историю с платком. Таким образом Отелло получил опровержение того, что Яго говорит правду. Отелло верит служанке, и это сразу же приводит к разрешению графа, но уже с противоположным результатом. Давайте посмотрим почему.


Теперь к нашему графу мы можем добавить вершины -20, +24, -21, -17, -18 (здесь представлена только правая часть графа):



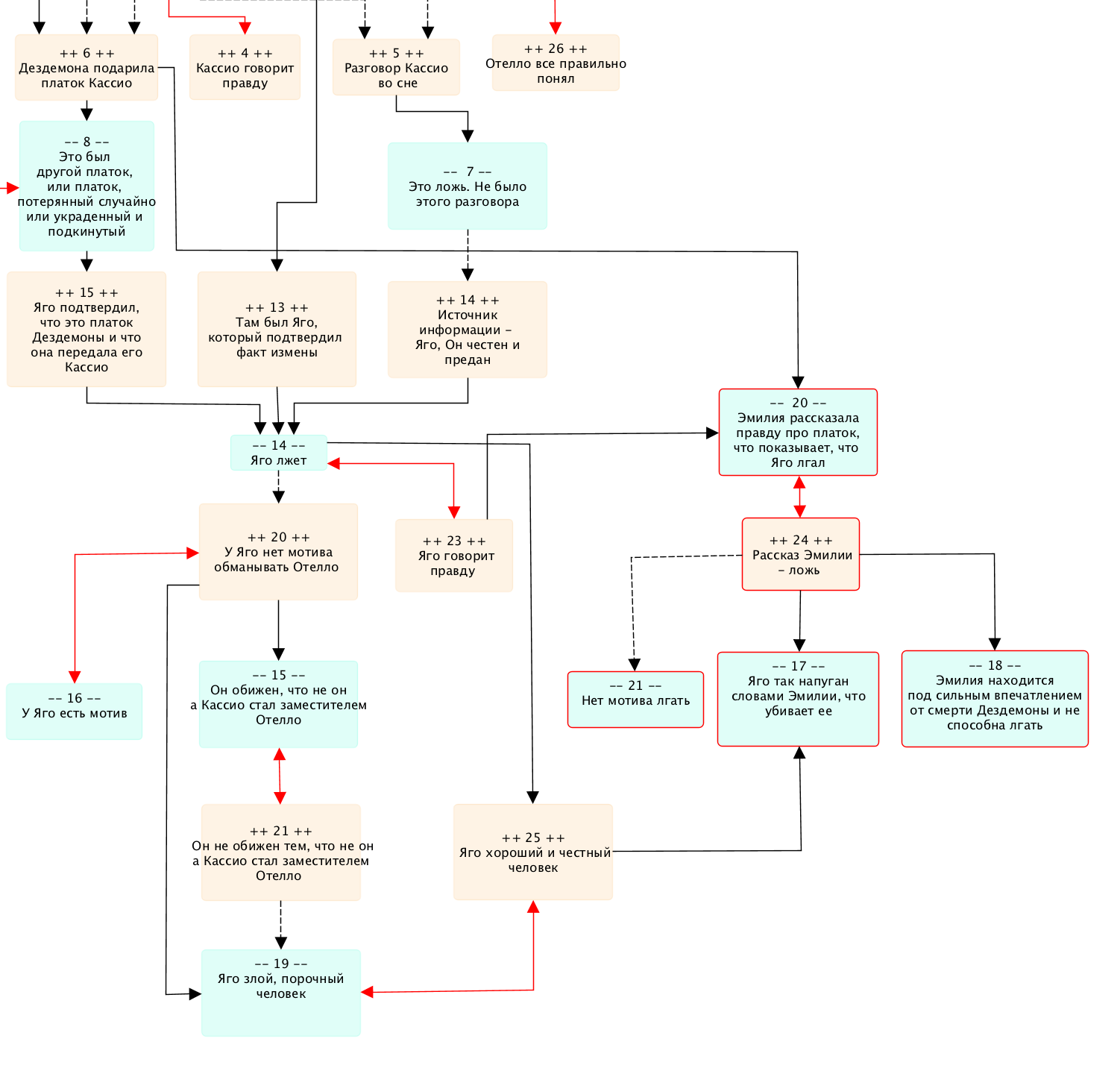
При этом -20<->+24 --п->-17 и -20<->+24 --п->-18 мы можем отнести к прямым доказательствам:


  • -20<->+24 --п->-17: "Эмилия рассказала правду про платок, что показывает, что Яго лгал", и это правда потому, что "Яго так напуган словами Эмилии, что убивает её"
  • -20<->+24 --п->-18: "Эмилия рассказала правду про платок, что показывает, что Яго лгал", и это правда потому, что "Эмилия находится под сильным впечатление от смерти Дездемоны и не способна лгать"

В действительности это не выглядит такими уж сильными аргументами, и "волну" можно продолжить и дальше. Например, возможно, Яго убивает Эмилию не потому, что она говорит правду, а по другой причине, или Эмилия лишь притворяется, что находится под сильным впечатлением. И при холодном анализе все это должно быть учтено. Но в данном случае интересно отношение Отелло, интересно то, как именно он все это воспринимает, а мавр поверил Эмилии.


Проанализируем наш граф теперь.


  • вершины -17 и -18 на нашем графе тупиковые. Значит, эти вершины, а также вершины +24 и +25 и все их связи мы помечаем как удаленные. Также мы удаляем вершину -21 вместе со связями, т.к. она потеряла связь с корнем графа
  • теперь вершины -19 и -20 становятся тупиковыми. Значит, эти вершины, а также вершины +6, +23 и +20 и все их связи можно удалить. Также удаляем и вершины, не имеющие пути к корню, то есть -16, -15, +21, -8, +15, + 22
  • теперь тупиковые вершины -14, -7. Удаляем их и вершины, которые они прямо опровергли: +13, +5

Получаем граф (только правое крыло):



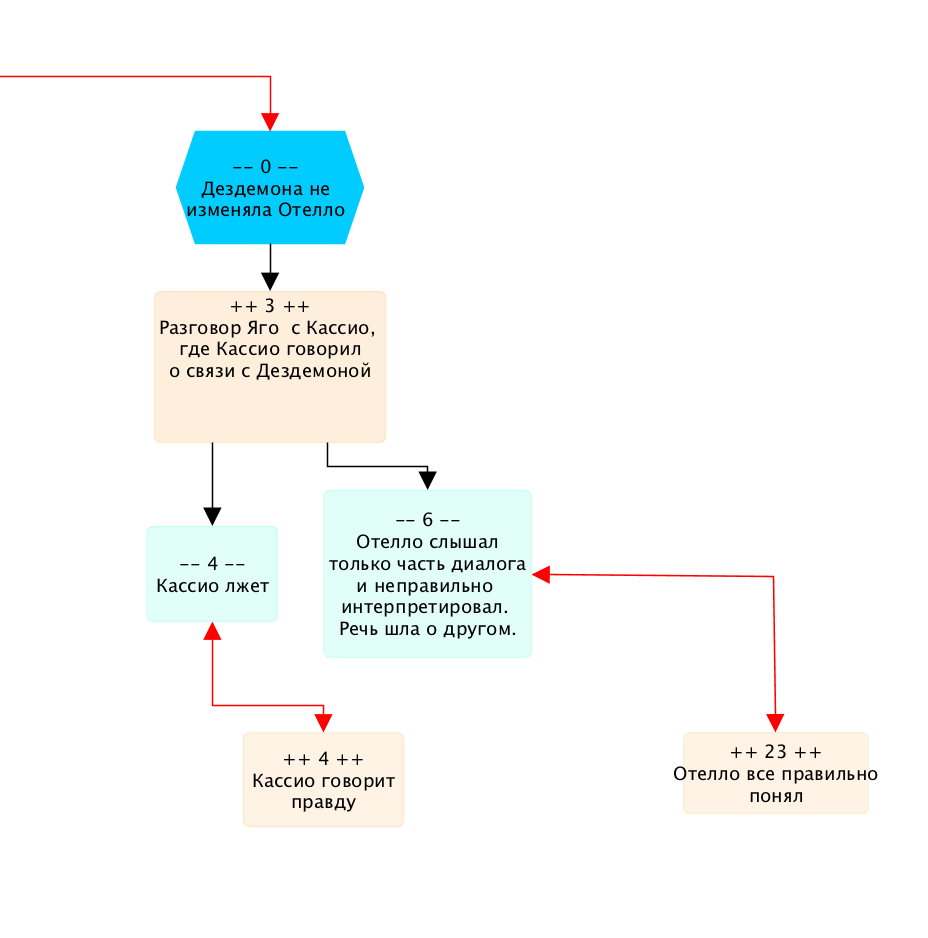
Даже после признания того, что Яго лжец, граф формально не сходится. Действительно, теперь Отелло знает, что Яго лжец, что история с платком была подстроена. Нет никаких доказательств того, что Дездемона изменила (также нет и никаких опровержений). Но Отелло лично слышал то, как Кассио рассказывал про свою связь с Дездемоной. При этом Отелло не знает, говорил ли Кассио правду, а также не знает, правильно ли он интерпретировал диалог, который услышал. Но у Отелло уже произошло "переключение" восприятие, поэтому он считает, что, так как все было подстроено, то и диалог был понят неверно. Поэтому вершина +23 удаляется, и вершина -6 становится тупиковой.


На следующем шаге это приводит к тому, что вершина +3 и с ней вершины -4 и +4 со всеми связями также удаляются, и вершина -0 остается без прямых и косвенных опровержений. Это значит, что все аргументы, как прямые, так и косвенные, подтверждающие, что Дездемона изменила были опровергнуты.


Что мы имеем в данной точке нашего анализа?


  • у нас не осталось ни одного аргумента, подтверждающего прямо или косвенно измену
  • у нас есть аргументы, опровергающие измену (недоказанные и неопровергнутые)
    Можно ли считать в данной точке граф разрешенным? Пока нет, потому что далее мы должны произвести анализ всех аргументов опровергающих измену, и может получиться следующая ситуация:

Такой граф говорит о том, что недостаточно данных. Это та ситуация, когда спорящие стороны упираются в неразрешимый "да-нет" цикл. Никто не может привести убедительных аргументов за или против, но по каким-то иррациональным причинам мнение сторон по этому вопросу является диаметрально противоположным.


Почему же граф сошелся для Отелло? Для этого давайте взглянем на его левую часть. Теперь все просто, вершины -13 ("Эмилия говорит правду") и -12 ( "Дездемона говорит правду") становятся тупиковыми (доказанными) в восприятии Отелло, и после этого граф легко разрешается.


Итак, что же произошло? Теперь, когда Отелло перестал верить Яго, он автоматически стал верить Дездемоне и Эмилии (что, в принципе, иррационально), и это привело к тому, что граф сошелся, но уже с противоположным результатом. Фаза восприятия мавра сдвинулась на 180 градусов.


Иррациональные элементы и опорные точки


В примере с Отелло мы видим, что изначальный граф не сходится. Чтобы граф сошелся, нужно было допустить иррациональность — поверить. Как только Отелло поверил Яго и перестал верить Дездемоне, граф сошелся. Отелло видит эту ситуацию в "желтых тонах" (он воспринимает все вершины с положительной нумерацией и желтым цветом, как истинные).


Потом, когда Отелло поверил Эмилии и соответственно осознал, что Дездемона говорила правду, а Яго лгал, фаза восприятия Отелло скачком сдвигается на 180 градусов, и для Отелло становятся истинными утверждения всех голубых вершин (отрицательная нумерация, голубой цвет).


Что же произошло? Отелло получил от Эмилии некоторую дополнительную информацию, но он даже не проверил, правдива ли она, а ведь Эмилия могла тоже обманывать, и холодный анализ требует построения "волны" доказательств/опровержений и для фактов, предоставленных Эмилией. Но мавр опять поверил. Да, в соответствии с той реальностью, которую предоставил нам Шекспир, в этот раз он не ошибся. Но, в жизни могло быть все не так, и на самом деле именно Яго мог бы быть истинным положительным героем, преданным и честным, попавшем в паутину интриги.


Итак, мы видим важную вещь: в основе принятия решения в обоих случаях лежал иррациональный элемент. Мавр должен был сделать выбор — кому верить, а кому нет (взаимоисключающий выбор). И это также отражено на волновом графе. Существуют особые вершины, которые мы будем называть опорными утверждениями (опорными вершинами или просто опорными точками), и эти вершины действительно являются опорой для восприятия ситуации, и вера в то истинны или ложны эти утверждения способны перевернуть картину мира.


Опорные утверждения — это минимальный набор самосогласованных утверждений (в идеале одно), в которые человек верит, что позволяет графу сойтись. В зависимости от того, с каким знаком эта вера (верит ли он, что эти/это утверждение истинно или ложно) граф сходится либо с положительным, либо с отрицательным результатом. На полном волновом графе (см. определение ниже) эти вершины являются частью неразрешимых циклов (скрытая информация).


Например, как мы видели в случае Отелло, было несколько опорных утверждений, связанных с доверием Яго, доверием Дездемоне и доверием служанке Эмилии. Согласованность заключалась в том, что, чтобы граф сошелся недостаточно было верить Яго, нужно было также не верить Дездемоне и Эмилии и, наоборот.


Пример 1

Опорные утверждения явно постулируются в некоторых мировоззрениях. Так, например, в религии вера является явно декламируемым требованием. Это может быть вера авторитетам, священным текстам и в некоторые концепции (столпы веры). Конечно, в каждой религии свой набор опорных элементов. Мировоззрение, близкое к религиозному, встречается не только во всевозможных сектах, но также и в некоторых формах государственного управления и даже в некоторых вполне коммерческих компаниях.

Замечание

Мы никак не обсуждаем вопрос истинности или ложности этих концепций здесь.

Удивительно, но иногда человек настолько ревностно оберегает свои опорные утверждения, что, защищая их, в попытке устранения явных противоречий с действительностью, к которым приводит ложная картина мира, основанная на ложных постулатах, может свято верить даже в самые невероятные вещи и не видеть или отрицать очевидное.


Пример 2

Вторым примером, который я бы хотел привести, является наука. Здесь тоже есть явно формулируемые опорные утверждения, например, математические аксиомы или фундаментальные законы физики. Принципиальное отличие от предыдущего примера заключается в том, что эти опорные утверждения постоянно проверяются на истинность, и, если наблюдается противоречие с экспериментом, то эти законы должны быть изменены таким образом, чтобы это противоречие устранить. Но все же эти утверждения продолжают быть опорными точками, потому что в действительности у них нет никакого логического обоснования (доказательства). Можно сказать, что ученые таким образом формулируют опорные точки самой природы.

Причинный анализ

На основе волнового графа мы можем построить "обратный" граф — с началом в опорной точке (или опорных точках) и по направлению к корневому утверждению. При этом мы могли бы использовать только одну связь — "поэтому правда то, что". Этот граф можно получить из волнового, если следовать по волновым логическим цепочкам от опорного утверждения в сторону корневого, но только по утверждениям, находящимся в той же фазе, что и опорное. Таким образом, мы также получаем последовательность утверждений, которые мы будем называть причинными логическими цепочками. В зависимости от того, верим ли мы в истинность или ложность опорного утверждения мы получаем два разных причинных графа (разные фазы волны).


Пример

Вернемся к нашему примеру с Отелло.


Рассмотрим два утверждения -14 ("Яго лжет") и его дополнение +23 ("Яго говорит правду").

Если утверждение +23 становится опорным (Отелло верит, что Яго говорит правду), то это опорное утверждение становится корнем для причинных логических цепочек, приводящих к тому, что Отелло начинает считать, что "Дездемона изменила Отелло". Например, цепочка +23 -> +13 ->+3 ->+0 (обратите внимание, что все вершины желтого цвета), выделенная желтыми стрелками на графе выше, означает, что

"Яго говорит правду, поэтому правда то, что Кассио сам лично рассказывал о связи с Дездемоной, поэтому это правда, что Дездемона изменила Отелло".

В случае же если -14 является опорным ("Яго лжет"), то фаза меняется на противоположную. Рассмотрим цепочку -14 -> -6 ->0 (все вершины голубые):

"Яго лжет, поэтому правда то, что мавр слышал лишь часть диалога и неверно интерпретировал этот диалог, поэтому Дездемона не изменяла Отелло".

Из вышеприведенного примера видно, что логическое обоснование здесь слабое, скорее напоминающее косвенные (а не прямые) связи волнового анализа. Так, например, то, что Кассио рассказывал о связи с Дездемоной (даже, если бы это было правдой) не следует, что Дездемона действительно изменила с ним Отелло. Это является следствием того, что в данном примере мы движемся вверх лишь по одной волне. Нужно учитывать все волны, что делает логику довольно сложной и, похоже, без критического восприятия и анализа наш мозг избирает более легкий путь движения вверх лишь по одной (или нескольким из многих) волновой цепочке, что делает логику уязвимой.


Аксиома волнового анализа


Введем понятия полного и абсолютно полного волновых графов.


Абсолютно полный волновой граф — это граф, на котором учтены все возможные волны.


Это значит, что волны этого графа опускаются в том числе и до фундаментальных вопросов, связанных с мирозданием, нашим восприятием, вопросам бытия… Например, простое утверждение "Я вижу стол" порождает волны о реальности/иллюзорности нашего мира, объективности/субъективности восприятия, о моем психическом состоянии, ...


Кажется довольно очевидным, что в силу погружения в подобные фундаментальные проблемы абсолютно полный волновой граф всегда содержит скрытую информацию, и подобные графы принципиально неразрешимы. Мы всегда упираемся в некоторые вещи, которые мы должны принять на веру (а чаще всего мы о них просто не думаем, воспринимая, как что-то очевидное).


Абсолютно полный граф — это скорее теоретическая концепция. На практике нет необходимости рассматривать все подобные "волны". Нужно следовать контексту беседы и не вносить излишней сложности и детализированности. Например, нет смысла в политических спорах обсуждать философско-теологические вопросы. Разумно принять некоторые вещи как данность в контексте обсуждаемой темы.


Если мы исключим не укладывающиеся в контекст беседы волны, то таким образом получим полный волновой граф.


Замечание

Возникает вопрос, где же проходит эта граница контекста беседы? На каком уровне глубины анализа разумно остановиться? Что мы готовы принять за аксиомы (и, следовательно, на веру) в нашем анализе?

Предположим, что нам удалось найти разумный уровень глубины анализа, соответствующий обсуждаемой проблеме, что значит, что мы имеем консенсус по поводу истинности/ложности неких атомарных утверждений. Но существует еще много точек сокрытия информации:


  • мы не можем точно сказать, что думает другой человек, и говорит ли он правду
  • мы не можем доверять восприятию человека: часто оно подводит
  • мы физически воспринимаем мир только из определенной точки, и, даже если мы свидетели чего-то, то видим/слышим лишь часть события
  • у людей плохая память
  • иногда люди намеренно лгут
  • иногда группы людей намеренно лгут
  • если мы говорим про электронику, то, проходя через руки людей, данные могут быть искажены
  • если мы говорим про математические алгоритмы, то они могут быть взломаны, или их применение может быть некорректным
  • ...

Как вывод сформулируем в качестве гипотезы следующее утверждение, которое мы будем называть основной аксиомой волнового анализа:


  • всегда есть скрытая информация, не позволяющая однозначно разрешить полный волной граф

Следствие:


  • если произошло разрешение волнового графа, то это говорит о наличии иррационального элемента, ошибке логики или о неполноте волнового графа

Это не математическое утверждение, скорее психологическое.
Идея данной аксиомы заключается в том, что у нас всегда есть волны, которые "доходят" до скрытой информации. Не всегда уместно их исследовать, но всегда можно найти тот уровень, где появятся скрытые данные. Зачем это делать? А зачем формулировать вопрос, с которым все согласны? Темы поднимаются лишь тогда, когда требуется анализ, что предполагает искать точки сомнения, и такие точки в принципе всегда есть.


Пояснение на примерах

Хотя мы и пользуемся словом аксиома, но здесь нет математической строгости, прежде всего в силу неопределенности понятия полноты, которое мы ввели выше. В основе этого понятия лежит соответствие контексту, которое мы никак не определили. Давайте рассмотрим 2 примера, которые возможно прояснят идею.


Пример 1. Заседание суда. Алиса утверждает, что была 1-го апреля 2020 года в 6 вечера дома. И суду надо понять не обманывает ли Алиса. В контексте данного анализа нас интересует информация свидетелей. Например, Боб и Ева были в этот день у нее гостях и подтверждают это. Здесь полный граф предполагает, как минимум, следующие волны


  • возможно они обманывают (нужно рассмотреть все возможные причины)
  • возможно им лишь казалось, что это было 6 часов (Алиса перевела стрелки часов, например)
  • возможно, как раз ровно в 6 Алиса незаметно для гостей отлучилась

Судья в конце концов должен или поверить, или нет в то, что свидетели говорят правду, а также в то, что они адекватно восприняли ситуацию, в которой находились. Без этой (или подобной) веры граф не получится разрешить. То есть обычно, в хоть сколько-нибудь сложных ситуациях, мы должны доверять или не доверять источникам информации, иначе граф не разрешится. Но, в данном случае, рассуждения о природе нашего восприятия и иллюзорности/реальности мира, а также о других вечных темах явно являются излишними.


Пример 2. Теперь возьмем что-то простое, например, утверждение "Я вижу стол". Итак, раз я сформулировал это утверждение и пытаюсь произвести анализ его истинности, то в силу "элементарности" (как известно нет ничего сложнее, чем элементарное) я должен изменить уровень глубины нашего исследования. Теперь общефилософские вопросы как раз уместны, и можно порассуждать о том, насколько этот мир реален, насколько я сам адекватен, что значит "вижу", что такое "настоящее"… То есть когда мы говорим о чем-то элементарном, то в действительности наш граф становится (или приближается) к абсолютно полному графу, и является неразрешимым (пока мы что-то не примем на веру, как данность, как аксиому).


Говорит ли введенная аксиома о том, что нельзя докопаться до истины?


Нет, не говорит, но говорит о том, что всегда есть утверждения, которые невозможно обосновать логически, и если нам нужно разрешить граф, то мы должны сделать иррациональный выбор. Но это не значит, что это обязательно ошибка.


Просто к логике, к знанию, к информации, нужно добавить что-то еще.


Я бы назвал это что-то адекватностью. О сложности и неоднозначности этого понятия мы уже подробно говорили в этой статье, но в любом случае важным компонентом адекватности является также эмоциональная зрелость и развитое чувство гармонии. Можно прекрасно владеть информацией, данными, логическим мышлением и быть при этом безумцем с искаженным восприятием.


Замечание

Мы думаем, мы верим, что мы рассуждаем объективно и рассудочно и приходим к определенным выводам часто в полной уверенности в своей правоте, и иногда испытываем настоящий шок (как было со мной) от того, что другие люди, близкие, умные, эрудированные, приходят к абсолютно противоположному выводу, на основе тех же данных, той же информации. Почему? Если допустить, что основная аксиома волнового анализа верна, то становится понятно почему.

Тот факт, что мы пришли к выводу и особенно то, что мы уверены в своей правоте говорит о том, что мы во что-то поверили. Тоже самое и с нашими оппонентами, но их "вера" другая. Мы имеем разную веру по поводу опорных точек нашего графа.

Типичные ошибки при ведении дискуссии


Волновой анализ также позволяет увидеть причины, почему спорить по старинке не эффективно.


Приведем список типичных ошибок ведения споров:


  • неполный граф. Спорящие не пытаются создать полный граф, например, принимают информацию без критического анализа, без попытки понять правда или нет, кто ее источник, какие намерения у автора...
  • логические ошибки. Например, косвенные аргументы принимаются за прямые
  • локальность анализа. Граф может быть довольно большим, со сложной топологией. Невозможно без специального инструмента держать в уме всю картину, поэтому спор сосредотачивается только в каком-то очень локальном месте. Обычно в споре у вас нет возможности сделать более чем несколько логических шагов
  • обсуждение несущественного. Вместо концентрации внимания на опорных точках спор ведется на периферии
  • закрытость. Спорящие часто бессознательно "охраняют" свои опорные точки и избегают их обсуждения
  • желание доказать правоту. Вместо попытки найти истину, понять, где ты сам можешь ошибаться, обычно спор сводится к желанию победить, применяется психологическое давление, что лишь усиливает наше нежелание действительно анализировать и искать ответы

Применение волнового анализа на практике


Пример с Отелло содержит около 50 вершин — и это довольно простой анализ. Когда я пытался применить данный подход к реальной ситуации, я имел сотни вершин со множеством связей. Я пользовался и пользуюсь yEd для этого, но все-же это не удобно. Надо также понимать, что каждая вершина — это не просто утверждение, это может быть небольшой статьей с описанием фактов и доказательной базой.


Нужно приложение. Вопросы удобства и автоматизации, конечно же, важны, но, что действительно необходимо, так это то, что это приложение должно давать возможность коллективного участия и контроля по принципу википедии. Это позволит максимально приблизить граф к полному волновому графу и избежать логических ошибок.


Так что же может дать нам волновой анализ на практике?


  • волновой граф позволяет найти опорные точки. Нет смысла обсуждать все волны, нужно сфокусироваться на опорных точках. До тех пор, пока ваш оппонент будет продолжать верить в то, во что он верит, его картина мира не изменится (также, как и ваша)

  • граф позволит проследить зависимость событий от опорных точек, даже если они расположены достаточно далеко друг от друга


    Замечание

    Я часто наблюдаю, как люди не могут увязать события между собой, просто потому, что между ними несколько логических шагов. Граф решает эту проблему

  • волновой граф позволит избавиться от логических ошибок
  • это просто экономия времени. После построения волнового графа можно будет не выслушивать и не повторять одно и то же. Если вы видите, что ход вашего рассуждения представляет новую волну, вы можете добавить ее
  • по нескольким утверждениям вашего оппонента вы можете достаточно точно сложить представление о его картине мира и его опорных точка
  • этот подход позволит каждому самому наглядно увидеть, что лежит в основе его картины мира и, возможно, попытаться дополнить свой граф, приближая его к полному

Принципы волнового анализа


В отличии от абстракций науки в реальной жизни мы часто имеем дело с сильно эмоционально заряженными событиями. Сознательно или бессознательно мы избегаем некоторые темы и придерживаем некоторые аргументы, хотя, возможно, они и вполне логичны. Порой наши споры и обсуждения — это минное поле со множеством табу, и если кто-то по неосторожности инициирует логическую цепочку с "запрещенным" оттенком, то сразу становится уязвим. Вас быстро могут причислить к фашистам, врагам, извращенцам, либерастам, расистам… названий для таких изгоев множество.


Если мы строим полный волновой граф, а ведь в этом и смысл, то нужно понимать, что все подобные табуированные темы тоже должны быть подняты. Если мы стремимся к адекватному восприятию, то мы не должны бояться подвергать анализу то, во что мы верим.


Поэтому в основе анализа несомненно должна лежать свобода в создании любых логических цепочек и… смелость, не только потому, что все мы боимся быть неверно истолкованными и потерять хорошие отношения (или даже приобрести врагов), но и потому, что в принципе никто не застрахован от того, что, подвергнув свои убеждения глубокому и честному анализу вы останетесь тем же человеком!