Данная статья представляет собой мою попытку выразить свой взгляд на следующие аспекты:
Бо́льшая часть данного поста базируется на материалах, подготовленных авторами fast.ai: [1], [2], [5] и [3], — представляя собой сжатую и предназначенную для максимально быстрого понимания сути вопроса версию их работы. Для ознакомления с деталями рекомендуется переходить по ссылкам, данным ниже.
Коэффициент скорости обучения – это гиперпараметр, определяющий порядок того, как мы будем корректировать наши весы с учётом функции потерь в градиентном спуске. Чем ниже величина, тем медленнее мы движемся по наклонной. Хотя при использовании низкого коэффициента скорости обучения мы можем получить положительный эффект в том смысле, чтобы не пропустить ни одного локального минимума, — это также может означать, что нам придётся затратить много времени на cходимость, особенно если мы попали в область плато.
Отношение иллюстрируется следующей формулой

Градиентный спуск с маленьким (вверху) и большим (внизу) коэффициентами скорости обучения. Источник: Andrew Ng’s Machine Learning course on Coursera
Чаще всего коэффициент скорости обучения устанавливается пользователем произвольно. В лучшем случае для интуитивного понимания того, какое значение более всего подходит для установления коэффициента скорости обучения, он может опираться на проведённые ранее эксперименты (или иной вид обучающего материала).
По существу достаточно трудно выбрать правильное значение. Приведённая ниже диаграмма наглядно показывает различные сценарии, которые могут возникнуть при самостоятельной настройке коэффициента скорости обучения пользователем.
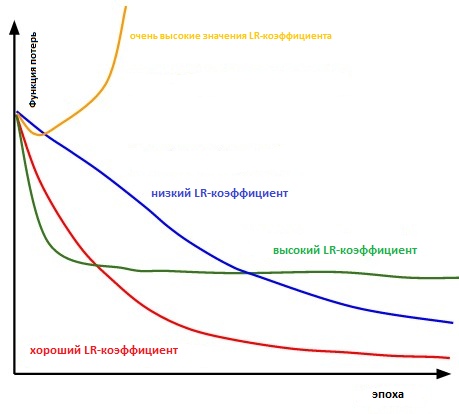
Влияние различных коэффициентов скорости обучения на сходимость. (Img Credit: cs231n)
Далее, коэффициент скорости обучения воздействует на то, как быстро наша модель достигнет локального минимума (aka достигнет наилучшей точности). Тем самым правильный выбор с самого начала гарантирует меньшую трату времени на тренировку модели. Чем меньше тренировочного времени, тем меньше средств тратится на вычислительные мощности GPU в облаке.
Есть ли более удобный способ определения коэффициент скорости обучения?
В параграфе 3.3. «Циклических коэффициентов скорости обучения для нейронных сетей» Лесли Смит отстаивал следующее положение: эффективность скорости обучения может быть оценена путём тренировки модели с изначально заданной низкой скоростью обучения, которая затем повышается (линейно или по экспоненте) в каждой итерации.
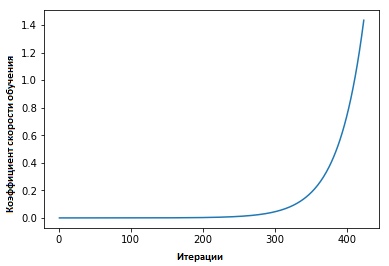
Коэффициент скорости обучения растёт после каждого мини-пакета.
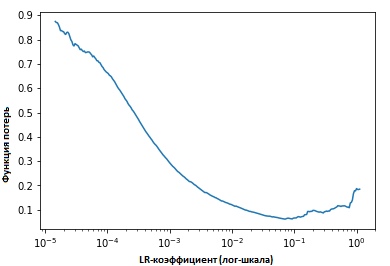
Фиксируя значения показателей на каждой итерации, мы увидим, что по мере повышения скорости обучения будет (достигнута) точка, в которой значения функции потерь перестаёт уменьшаться и начинает увеличиваться. На практике наша скорость обучения в идеальном варианте должна быть где-то слева от нижней точки на графике (как показано на графике ниже). В этом случае (значение будет) от 0.001 до 0.01.
На данный момент есть готовая функция в пакете fast.ia, разработанная Джереми Ховардом, это своего рода абстракция/надстройка поверх библиотеки pytorch (наподобие того, как это сделано в случае с Keras и Tensorflow).
Необходимо лишь ввести следующую команду для того чтобы начать поиск оптимального коэффициента скорости обучения, прежде нежели (начать) тренировать нейронную сеть.
Итак, мы рассказали, что такое коэффициент скорости обучения, каково его значение и каким образом можно достичь его оптимального значения прежде, чем начать тренировать саму модель.
Теперь мы остановимся на том, как коэффициент скорости обучения может быть использован для тюнинга моделей.
Обычно, когда пользователь устанавливает свой коэффициент скорости обучения и приступает к тренировке модели, ему необходимо подождать до тех пор, пока коэффициент скорости обучения не начнёт падать и модель не достигнет оптимального значения.
Однако с того момента, как градиент достигнет плато, улучшить значения функции потерь при обучении модели становится тяжелее. В [3] Dauphin высказывает точку зрения о том, что сложность в минимизации функции потерь проистекает от седловой точки, а не от локального минимума.

Седловая точка на поверхности ошибок. Седловая точка – такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. (ImgCredit: safaribooksonline)
Предлагаю рассмотреть несколько вариантов. Один из них, общий, — пользуясь цитатой из [1],
В [2] Лесли предлагает «метод треугольников», в котором коэффициент скорости обучения пересматривается после каждой из нескольких итераций.

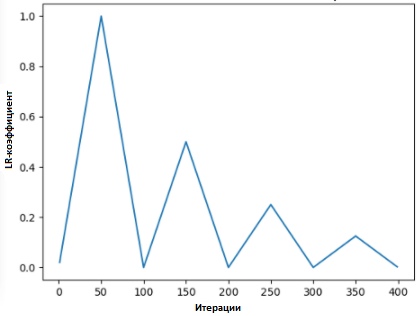
«Метод треугольников» и «метод треугольников-2» — методы для циклического тестирования коэффициентов скорости обучения, предложенные Лесли Н. Смитом. На верхнем графике минимальный и максимальный Ir сохраняются равными.
Другой метод, обладающий не меньшей популярностью и носящий название «Стохастический градиентный спуск с тёплой перезагрузкой», был предложен Lonchilov & Hutter [6]. Данный метод, в основе которого лежит использование функции косинуса как циклической, перезапускает коэффициент скорости обучения в точке максимума в каждом цикле. Появление «Горячего» бита связано с тем, что при перезапуске коэффициента скорости обучения он начинается не с нулевого уровня, а от параметров, до которых модель дошла за предыдущий шаг.
Поскольку у данного метода существуют вариации, приведённый ниже график демонстрирует один из способов его применения, где каждый цикл привязан к одинаковому временному отрезку.

SGDR –график, коэффициент скорости обучения vs. итераций
Тем самым мы получаем способ сократить продолжительность тренировки, просто время от времени перепрыгивая «вершины» (как показано ниже).

Сравнение фиксированного и циклического коэффициентов скорости обучения (img credit: arxiv.org/abs/1704.00109
Дополнительно к экономии времени данный метод, согласно исследованиям, улучшает точность классификации без тюнинга и за меньшее число итераций.
В курсе fast.ai акцент сделан на управление предварительно обученной моделью при решении проблем искусственного интеллекта. Например, при решении проблем классификации изображений студентов обучают пользованию такими заранее обученными моделями как VGG и Resnet50 и увязыванию их к той выборке данных изображений, которые необходимо предсказать.
Чтобы подытожить, как происходит построение модели в программе fast.ai (не следует путать с fast. ai package – пакетом из программы), ниже мною приведены шаги, которые мы будем предпринимать в обыкновенной ситуации:
Можно заметить, что шаги второй, пятый и седьмой (из приведённых выше) связаны с коэффициент скорости обучения. В более ранней части нашего поста мы осветили пункт второй упомянутых шагов – где коснулись того, как получить наилучший коэффициент скорости обучения прежде, нежели начать тренировку модели.
В последующем абзаце мы рассказали, как путём использования SGDR можно сократить тренировочное время, а благодаря периодическому перезапуску коэффициента скорости обучения – повысить точность, с тем чтобы в последующем избежать областей, где градиент близок к нулю.
В последней секции мы затронем понятие дифференцированного обучения и поясним, каким образом оно применяется для определения коэффициента скорости обучения, когда обучаемая модель связывается с заранее обученной…
Это метод, при котором во время тренировки в сети устанавливаются различные коэффициенты скорости обучения. Он представляет собой альтернативу тому способу, которым пользователи обыкновенно настраивают коэффициенты скорости обучения – а именно использованию одного и того же коэффициента скорости обучения сквозь сеть во время тренировки.

Причина, по которой я люблю Твиттер, — прямой ответ от самого человека.
(Во время написания этого поста Джереми опубликовал статью с Себастьяном Рудером, который ещё глубже погрузился в эту тему. Так что, я полагаю, дифференциальный коэффициент скорости обучения имеет теперь и другое название – дискриминационный точный тюнинг :)
Чтобы нагляднее продемонстрировать концепцию, мы можем сослаться на приведённую ниже диаграмму, на которой заранее обученная модель «расколота» на 3 группы, где каждая настраивается с возрастающей величиной коэффициента скорости обучения.

Пример CNN с дифференцированным коэффициентом скорости обучения. Image credit from [3]
За этим методом конфигурации стоит следующее понимание: первые несколько слоёв обыкновенно содержат очень мелкие детали данных, такие как линии и углы – из которых мы не будем пытаться изменить много и постараемся сохранить имеющуюся в них информацию. В целом нет серьёзной необходимости менять их веса на какое-либо большо́е число.
Напротив, для последующих слоёв,- таких как те, что на картинке окрашены в зелёный цвет, где мы получаем детализированные признаки данных, как то: белки глаз, или рот, или нос – необходимость сохранять их исчезает.
В [9] доказывается, что точная настройка целой модели будет чересчур затратной, так как пользователи могут получить свыше 100 слоёв. Чаще всего люди прибегают к оптимизации модели на один слой за раз.
Однако, это является причиной ряда требований, т.н. мешающего параллелизма, и требует множественных входов через набор данных, что приводит к чрезмерному обучению маленьких наборов.
Также нами было показано, что методы, представленные в [9], способны как улучшить точность, так и сократить количество ошибок в различных заданиях, связанных с NRL классификацией.

Результаты взяты из источника [9]
References:
[1] Improving the way we work with learning rate.
[2] The Cyclical Learning Rate technique.
[3] Transfer Learning using differential learning rates.
[4] Leslie N. Smith. Cyclical Learning Rates for Training Neural Networks.
[5] Estimating an Optimal Learning Rate for a Deep Neural Network
[6] Stochastic Gradient Descent with Warm Restarts
[7] Optimization for Deep Learning Highlights in 2017
[8] Lesson 1 Notebook, fast.ai Part 1 V2
[9] Fine-tuned Language Models for Text Classification
- Что такое коэффициент скорости обучения и каково его значение?
- Как подбирать данный коэффициент при обучении моделей?
- Почему необходимо менять коэффициент скорости обучения в процессе тренировки моделей?
- Как поступать с коэффициентом скорости обучения, когда используется предварительно обученная модель?
Бо́льшая часть данного поста базируется на материалах, подготовленных авторами fast.ai: [1], [2], [5] и [3], — представляя собой сжатую и предназначенную для максимально быстрого понимания сути вопроса версию их работы. Для ознакомления с деталями рекомендуется переходить по ссылкам, данным ниже.
Что такое коэффициент скорости обучения?
Коэффициент скорости обучения – это гиперпараметр, определяющий порядок того, как мы будем корректировать наши весы с учётом функции потерь в градиентном спуске. Чем ниже величина, тем медленнее мы движемся по наклонной. Хотя при использовании низкого коэффициента скорости обучения мы можем получить положительный эффект в том смысле, чтобы не пропустить ни одного локального минимума, — это также может означать, что нам придётся затратить много времени на cходимость, особенно если мы попали в область плато.
Отношение иллюстрируется следующей формулой

Градиентный спуск с маленьким (вверху) и большим (внизу) коэффициентами скорости обучения. Источник: Andrew Ng’s Machine Learning course on Coursera
Чаще всего коэффициент скорости обучения устанавливается пользователем произвольно. В лучшем случае для интуитивного понимания того, какое значение более всего подходит для установления коэффициента скорости обучения, он может опираться на проведённые ранее эксперименты (или иной вид обучающего материала).
По существу достаточно трудно выбрать правильное значение. Приведённая ниже диаграмма наглядно показывает различные сценарии, которые могут возникнуть при самостоятельной настройке коэффициента скорости обучения пользователем.

Влияние различных коэффициентов скорости обучения на сходимость. (Img Credit: cs231n)
Далее, коэффициент скорости обучения воздействует на то, как быстро наша модель достигнет локального минимума (aka достигнет наилучшей точности). Тем самым правильный выбор с самого начала гарантирует меньшую трату времени на тренировку модели. Чем меньше тренировочного времени, тем меньше средств тратится на вычислительные мощности GPU в облаке.
Есть ли более удобный способ определения коэффициент скорости обучения?
В параграфе 3.3. «Циклических коэффициентов скорости обучения для нейронных сетей» Лесли Смит отстаивал следующее положение: эффективность скорости обучения может быть оценена путём тренировки модели с изначально заданной низкой скоростью обучения, которая затем повышается (линейно или по экспоненте) в каждой итерации.

Коэффициент скорости обучения растёт после каждого мини-пакета.
Фиксируя значения показателей на каждой итерации, мы увидим, что по мере повышения скорости обучения будет (достигнута) точка, в которой значения функции потерь перестаёт уменьшаться и начинает увеличиваться. На практике наша скорость обучения в идеальном варианте должна быть где-то слева от нижней точки на графике (как показано на графике ниже). В этом случае (значение будет) от 0.001 до 0.01.

Приведённое выше выглядит полезным. Как начать использовать это?
На данный момент есть готовая функция в пакете fast.ia, разработанная Джереми Ховардом, это своего рода абстракция/надстройка поверх библиотеки pytorch (наподобие того, как это сделано в случае с Keras и Tensorflow).
Необходимо лишь ввести следующую команду для того чтобы начать поиск оптимального коэффициента скорости обучения, прежде нежели (начать) тренировать нейронную сеть.
learn.lr_find()
learn.sched.plot_lr()
Улучшая модель
Итак, мы рассказали, что такое коэффициент скорости обучения, каково его значение и каким образом можно достичь его оптимального значения прежде, чем начать тренировать саму модель.
Теперь мы остановимся на том, как коэффициент скорости обучения может быть использован для тюнинга моделей.
Конвенциональная мудрость
Обычно, когда пользователь устанавливает свой коэффициент скорости обучения и приступает к тренировке модели, ему необходимо подождать до тех пор, пока коэффициент скорости обучения не начнёт падать и модель не достигнет оптимального значения.
Однако с того момента, как градиент достигнет плато, улучшить значения функции потерь при обучении модели становится тяжелее. В [3] Dauphin высказывает точку зрения о том, что сложность в минимизации функции потерь проистекает от седловой точки, а не от локального минимума.

Седловая точка на поверхности ошибок. Седловая точка – такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. (ImgCredit: safaribooksonline)
Итак, как же можно избежать этого?
Предлагаю рассмотреть несколько вариантов. Один из них, общий, — пользуясь цитатой из [1],
…вместо того, чтобы использовать фиксированную величину для коэффициента скорости обучения и уменьшать его с течением времени, в том случае если тренировка больше не сглаживает нашу потерю, мы собираемся менять коэффициент скорости обучения в каждой итерации согласно некоторой циклической функции f. Каждый цикл имеет – в вопросе числа итераций – фиксированную длину. Данный метод позволяет коэффициенту скорости обучения варьировать между разумными граничными значениями. Это реально помогает, потому что, увязнув в седловых точках, мы путём увеличения коэффициент скорости обучения получим более быстрое пересечение плато седловых точек
В [2] Лесли предлагает «метод треугольников», в котором коэффициент скорости обучения пересматривается после каждой из нескольких итераций.


«Метод треугольников» и «метод треугольников-2» — методы для циклического тестирования коэффициентов скорости обучения, предложенные Лесли Н. Смитом. На верхнем графике минимальный и максимальный Ir сохраняются равными.
Другой метод, обладающий не меньшей популярностью и носящий название «Стохастический градиентный спуск с тёплой перезагрузкой», был предложен Lonchilov & Hutter [6]. Данный метод, в основе которого лежит использование функции косинуса как циклической, перезапускает коэффициент скорости обучения в точке максимума в каждом цикле. Появление «Горячего» бита связано с тем, что при перезапуске коэффициента скорости обучения он начинается не с нулевого уровня, а от параметров, до которых модель дошла за предыдущий шаг.
Поскольку у данного метода существуют вариации, приведённый ниже график демонстрирует один из способов его применения, где каждый цикл привязан к одинаковому временному отрезку.

SGDR –график, коэффициент скорости обучения vs. итераций
Тем самым мы получаем способ сократить продолжительность тренировки, просто время от времени перепрыгивая «вершины» (как показано ниже).

Сравнение фиксированного и циклического коэффициентов скорости обучения (img credit: arxiv.org/abs/1704.00109
Дополнительно к экономии времени данный метод, согласно исследованиям, улучшает точность классификации без тюнинга и за меньшее число итераций.
Коэффициент скорости обучения в Transfer learning
В курсе fast.ai акцент сделан на управление предварительно обученной моделью при решении проблем искусственного интеллекта. Например, при решении проблем классификации изображений студентов обучают пользованию такими заранее обученными моделями как VGG и Resnet50 и увязыванию их к той выборке данных изображений, которые необходимо предсказать.
Чтобы подытожить, как происходит построение модели в программе fast.ai (не следует путать с fast. ai package – пакетом из программы), ниже мною приведены шаги, которые мы будем предпринимать в обыкновенной ситуации:
- Включим data augmentation и precompute=True
- Используйте Ir_find () для нахождения наибольшего коэффициента скорости обучения, где потеря по-прежнему явно улучшается.
- Тренируйте последний слой из заранее вычисленных активаций для 1-2 эпохи.
- Тренировать последний слой с приростом данных (т.е. предвычислить=false) на 1-2 эпохи с циклом _len 1.
- Разморозить все слои.
- Поместить более ранние слои на коэффициент скорости обучения, который был бы на 3x-10x ниже следующего высокого слоя
- Вновь использовать Ir_find()
- Тренировать полную сеть с циклом _mult=2 =2 пока она не начнет переобучаться.
Можно заметить, что шаги второй, пятый и седьмой (из приведённых выше) связаны с коэффициент скорости обучения. В более ранней части нашего поста мы осветили пункт второй упомянутых шагов – где коснулись того, как получить наилучший коэффициент скорости обучения прежде, нежели начать тренировку модели.
В последующем абзаце мы рассказали, как путём использования SGDR можно сократить тренировочное время, а благодаря периодическому перезапуску коэффициента скорости обучения – повысить точность, с тем чтобы в последующем избежать областей, где градиент близок к нулю.
В последней секции мы затронем понятие дифференцированного обучения и поясним, каким образом оно применяется для определения коэффициента скорости обучения, когда обучаемая модель связывается с заранее обученной…
Что такое дифференцированное обучение
Это метод, при котором во время тренировки в сети устанавливаются различные коэффициенты скорости обучения. Он представляет собой альтернативу тому способу, которым пользователи обыкновенно настраивают коэффициенты скорости обучения – а именно использованию одного и того же коэффициента скорости обучения сквозь сеть во время тренировки.

Причина, по которой я люблю Твиттер, — прямой ответ от самого человека.
(Во время написания этого поста Джереми опубликовал статью с Себастьяном Рудером, который ещё глубже погрузился в эту тему. Так что, я полагаю, дифференциальный коэффициент скорости обучения имеет теперь и другое название – дискриминационный точный тюнинг :)
Чтобы нагляднее продемонстрировать концепцию, мы можем сослаться на приведённую ниже диаграмму, на которой заранее обученная модель «расколота» на 3 группы, где каждая настраивается с возрастающей величиной коэффициента скорости обучения.

Пример CNN с дифференцированным коэффициентом скорости обучения. Image credit from [3]
За этим методом конфигурации стоит следующее понимание: первые несколько слоёв обыкновенно содержат очень мелкие детали данных, такие как линии и углы – из которых мы не будем пытаться изменить много и постараемся сохранить имеющуюся в них информацию. В целом нет серьёзной необходимости менять их веса на какое-либо большо́е число.
Напротив, для последующих слоёв,- таких как те, что на картинке окрашены в зелёный цвет, где мы получаем детализированные признаки данных, как то: белки глаз, или рот, или нос – необходимость сохранять их исчезает.
Как это соотносится с другими методами точной настройки?
В [9] доказывается, что точная настройка целой модели будет чересчур затратной, так как пользователи могут получить свыше 100 слоёв. Чаще всего люди прибегают к оптимизации модели на один слой за раз.
Однако, это является причиной ряда требований, т.н. мешающего параллелизма, и требует множественных входов через набор данных, что приводит к чрезмерному обучению маленьких наборов.
Также нами было показано, что методы, представленные в [9], способны как улучшить точность, так и сократить количество ошибок в различных заданиях, связанных с NRL классификацией.

Результаты взяты из источника [9]
References:
[1] Improving the way we work with learning rate.
[2] The Cyclical Learning Rate technique.
[3] Transfer Learning using differential learning rates.
[4] Leslie N. Smith. Cyclical Learning Rates for Training Neural Networks.
[5] Estimating an Optimal Learning Rate for a Deep Neural Network
[6] Stochastic Gradient Descent with Warm Restarts
[7] Optimization for Deep Learning Highlights in 2017
[8] Lesson 1 Notebook, fast.ai Part 1 V2
[9] Fine-tuned Language Models for Text Classification

