Факторизация неотрицательных матриц (NMF) — это представление матрицы V в виде произведения матриц W и H, в котором все элементы трех матриц неотрицательны. Это разложение используется в различных областях знаний, например, в биологии, компьютерном зрении, рекомендательных системах. В этой публикации пойдет речь о таблицах сопряженности социологических и маркетинговых данных, факторизация которых помогает понять структуру данных этих таблиц.

Удивительно, но на Хабре, видимо, еще не писали о NMF. История этого метода и общие сведения доступны в Википедии (eng). Но сначала ответим на вопрос зачем вообще как-либо преобразовывать таблицы сопряженности.
Если число строк и столбцов в таблице небольшое, то достаточно простой диаграммы со столбцами или stacked bar графика, чтобы иметь представление о данных таблицы. Например, таблица полученная пересечением переменных «пол» и «частота посещения спортивных или фитнес клубов за последний месяц (4 категории)» размера 2х4 может быть легко проанализирована. Другое дело, если размер таблицы вырастает, скажем до 20х30 или более. В джунглях цифр таблицы и в лесу столбцов графика обнаружить закономерности будет невозможно или крайне затруднительно. В этом случае альтернативой является NMF, которое понижает размерность таблицы сопряженности и отображает результат в виде тепловых карт. Это дает крайне наглядное и легко интерпретируемое представление о таблице.
Исторически одним из первых методов графического представления структуры преобразованной таблицы является анализ соответствий (CA). Он восходит к методу главных компонент, и основан на сингулярном разложении матрицы (SVD). Об SVD можно почитать в этой статье на Хабре. Там же упоминается превосходное видео с определением SVD и примером построения анализа соответствий. Анализ соответствий популярный метод, но факторизация неотрицательных матриц, на мой взгляд, имеет ряд преимуществ. Соображения по этому поводу будут представлены в конце этой статьи.
Далее даны только те определения факторизации, которые необходимы для анализа таблиц сопряженности. Пусть таблица V имеет размер m x n. Обозначим через r ранг матриц W и H, как правило r << min(n,m). В отличии от точного представления матрицы в SVD, в NMF имеем только приближенное равенство
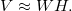
Матрицы W и H выбираются таким образом, чтобы минимизировать функцию потерь: D(V, WH) -> min. В нашем случае D задается на основе дивергенции Кульбака-Лейблера
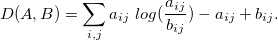
Остается вопрос с выбором ранга r. Есть несколько методов для оценки r (как, например, и в случае параметра k в методе k-средних). Но лучше вопрос выбора r оставить на усмотрения исследователя/пользователя, тот ранг, при котором структура таблиц наиболее понятна, проста, уместна, и является оптимальным.
В среде R есть пакет nmf [1], в котором реализованы несколько алгоритмов факторизации неотрицательных матриц, визуализации разложения и его диагностика. Возможности NMF будут продемонстрированы на данных 6 раунда европейского социального исследования (ESS). В предыдущей публикации было показано как можно загрузить эти данные в R.
В ESS проекте 2012 года принимало участие 29 стран. В анкету, в частности, был включен 21 вопрос о степени важности человеческих ценностей со шкалой из шести значений: от «Very much like me» до «Not like me at all». Каждую из этих 21 single response переменной преобразуем в логическую переменную. Значение True эта переменная принимает для тех респондентов, кому эта ценность важна — «Very much like me» и «Like me»; для всех остальных респондентов — сомневающихся, для тех кто не разделяет этой ценности или не ответивших, переменная принимает значение False.
Определим генеральную совокупность как «Мужчины возраста 20-45 лет». Строим таблицу пересечений этих логических переменных с каждой из 29 стран исследования, учитывая веса респондентов. Получаем таблицу размера 29х21.
Обратите внимание, таблица сопряженности воспринимается в расширенном смысле, она содержит multiple response переменную о человеческих ценностях. Кроме того, размеры ген. совокупности в каждой стране различны. По причине этих двух особенностей таблицы важно нормировать ее строки по размеру ген. совокупностей стран. То есть таблица состоит из взвешенных средних значений поддержки ценностей в каждой стране ESS исследования. Это ее фрагмент

Теперь строим теплокарты матриц W и H. Они определяют разложение исследуемых характеристик в пространстве 5 латентных переменных. Чем темнее клетка, тем более выражено соответствие между латентной переменной и ценностью или страной. Я опускаю математические детали точного определения, подробности можно найти в [1].
Далее отбираем лишь те human.values переменные, которые выражены только по одной из осей в этом пространстве. Названия осей даны мной самостоятельно.

Ниже показан итоговый результат — представление всех 29 стран. Цветом выражены степени соответствия переменных. К тому же страны группируются следуя иерархической кластеризации с евклидовой метрикой в 5-мерном пространстве латентных переменных.
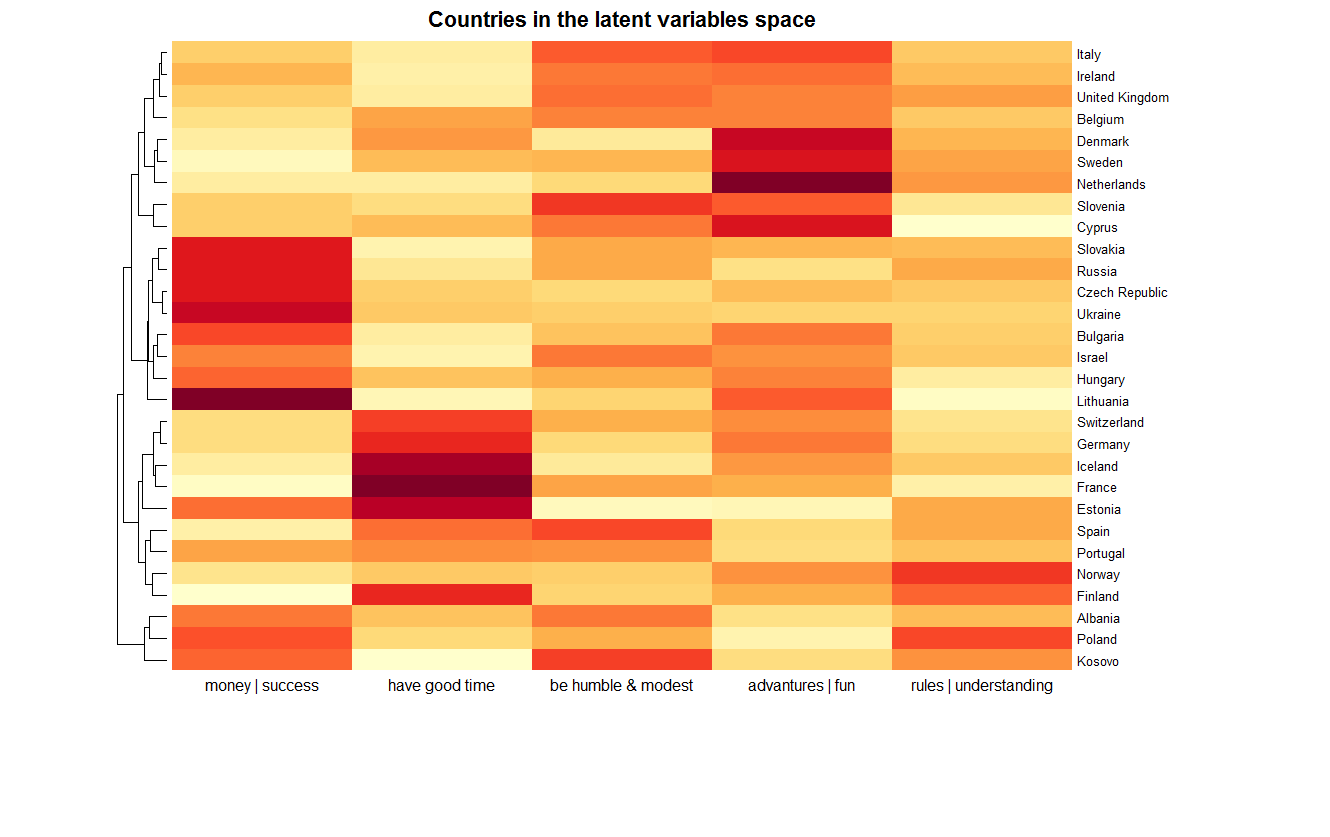
Видим, что в этом пространстве наиболее близкая страна к России — Словакия. Эти страны, в частности, выделяются выраженностью по первой оси, чего нельзя сказать, например, о Франции. Подробнее этот момент будет рассмотрен в следующей части статьи. Диаграмма также показывает какие страны составляют кластеры, в зависимости от требуемой подробности. Например, кластер из стран восточной Европы (Словакия, Россия, Чехия, Украина, Болгария, Венгрия, Литва) и Израиля. Любопытный кластер из Албании, Косово и… Польши. А Норвегия с Финляндией достаточно далеко расположены от Дании со Швецией.
С применением NMF для маркетинговой таблицы сопряженности можно познакомиться в этой публикации. В ней рассмотрен пример анализа восприятия 14 автомобильных марок.
Диаграммы NMF, на сколько хороши бы они не были, в общем случае, не дают оснований делать доказательные выводы о сходствах и различиях разных стран относительно представлений о ценностях. Эта задача будет рассмотрена в следующей части статьи.
Литература:
[1] Renaud Gaujoux et al. A flexible R package for nonnegative matrix factorization. In: BMC Bioinformatics 11.1 (2010), p. 367.

Удивительно, но на Хабре, видимо, еще не писали о NMF. История этого метода и общие сведения доступны в Википедии (eng). Но сначала ответим на вопрос зачем вообще как-либо преобразовывать таблицы сопряженности.
Если число строк и столбцов в таблице небольшое, то достаточно простой диаграммы со столбцами или stacked bar графика, чтобы иметь представление о данных таблицы. Например, таблица полученная пересечением переменных «пол» и «частота посещения спортивных или фитнес клубов за последний месяц (4 категории)» размера 2х4 может быть легко проанализирована. Другое дело, если размер таблицы вырастает, скажем до 20х30 или более. В джунглях цифр таблицы и в лесу столбцов графика обнаружить закономерности будет невозможно или крайне затруднительно. В этом случае альтернативой является NMF, которое понижает размерность таблицы сопряженности и отображает результат в виде тепловых карт. Это дает крайне наглядное и легко интерпретируемое представление о таблице.
Исторически одним из первых методов графического представления структуры преобразованной таблицы является анализ соответствий (CA). Он восходит к методу главных компонент, и основан на сингулярном разложении матрицы (SVD). Об SVD можно почитать в этой статье на Хабре. Там же упоминается превосходное видео с определением SVD и примером построения анализа соответствий. Анализ соответствий популярный метод, но факторизация неотрицательных матриц, на мой взгляд, имеет ряд преимуществ. Соображения по этому поводу будут представлены в конце этой статьи.
Далее даны только те определения факторизации, которые необходимы для анализа таблиц сопряженности. Пусть таблица V имеет размер m x n. Обозначим через r ранг матриц W и H, как правило r << min(n,m). В отличии от точного представления матрицы в SVD, в NMF имеем только приближенное равенство
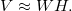
Матрицы W и H выбираются таким образом, чтобы минимизировать функцию потерь: D(V, WH) -> min. В нашем случае D задается на основе дивергенции Кульбака-Лейблера
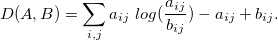
Остается вопрос с выбором ранга r. Есть несколько методов для оценки r (как, например, и в случае параметра k в методе k-средних). Но лучше вопрос выбора r оставить на усмотрения исследователя/пользователя, тот ранг, при котором структура таблиц наиболее понятна, проста, уместна, и является оптимальным.
В среде R есть пакет nmf [1], в котором реализованы несколько алгоритмов факторизации неотрицательных матриц, визуализации разложения и его диагностика. Возможности NMF будут продемонстрированы на данных 6 раунда европейского социального исследования (ESS). В предыдущей публикации было показано как можно загрузить эти данные в R.
В ESS проекте 2012 года принимало участие 29 стран. В анкету, в частности, был включен 21 вопрос о степени важности человеческих ценностей со шкалой из шести значений: от «Very much like me» до «Not like me at all». Каждую из этих 21 single response переменной преобразуем в логическую переменную. Значение True эта переменная принимает для тех респондентов, кому эта ценность важна — «Very much like me» и «Like me»; для всех остальных респондентов — сомневающихся, для тех кто не разделяет этой ценности или не ответивших, переменная принимает значение False.
Определим генеральную совокупность как «Мужчины возраста 20-45 лет». Строим таблицу пересечений этих логических переменных с каждой из 29 стран исследования, учитывая веса респондентов. Получаем таблицу размера 29х21.
Обратите внимание, таблица сопряженности воспринимается в расширенном смысле, она содержит multiple response переменную о человеческих ценностях. Кроме того, размеры ген. совокупности в каждой стране различны. По причине этих двух особенностей таблицы важно нормировать ее строки по размеру ген. совокупностей стран. То есть таблица состоит из взвешенных средних значений поддержки ценностей в каждой стране ESS исследования. Это ее фрагмент

Код построения таблицы и нахождения ее факторизации ранга 5.
Данные исследования уже загружены, имена объектов остались без изменений.
Перечисляем имена переменных в базе исследования соответствующих вопросам о человеческих ценностях
Добавляем в базу логические переменные, конвертированные в numeric тип и умноженные на веса респондентов
Строим требуемую таблицу (обозначена через cntry.human.values)
И выполняем факторизацию неотрицательных матриц ранга 5
Перечисляем имена переменных в базе исследования соответствующих вопросам о человеческих ценностях
human.values <- c("ipcrtiv", "imprich", "ipeqopt", "ipshabt", "impsafe", "impdiff", "ipfrule",
"ipudrst", "ipmodst", "ipgdtim", "impfree", "iphlppl", "ipsuces", "ipstrgv",
"ipadvnt", "ipbhprp", "iprspot", "iplylfr", "impenv", "imptrad", "impfun")
Добавляем в базу логические переменные, конвертированные в numeric тип и умноженные на веса респондентов
weighted.human.values<-paste(human.values,"w",sep="_")
add.binary.human.values<-function(){
adding.variables<-paste("srv.data[,c('", paste(weighted.human.values, collapse = "','"), "'):=list(",
paste("as.numeric(",human.values, " %in% c( 'Very much like me', 'Like me' ))
*dweight", collapse = ", " ), ")]", sep="")
eval(parse(text=adding.variables))
return(T)
}
add.binary.human.values()
Строим требуемую таблицу (обозначена через cntry.human.values)
target.audience.data <- srv.data[gndr == 'Male' & agea >= 25 & agea<=40,
c(weighted.human.values,'dweight', 'cntry'), with=FALSE]
cntry.human.values <- t(sapply(unique(target.audience.data[,cntry]), function(x)
colSums(target.audience.data[J(x)][,weighted.human.values,with=FALSE])))
cntry.pop.sizes <- target.audience.data[,list(W.Total=sum(dweight)),by=cntry]
cntry.human.values <- cntry.human.values/cntry.pop.sizes[,W.Total]*100
rownames(cntry.human.values) <- c("Albania", "Belgium", "Bulgaria", "Switzerland", "Cyprus",
"Czech Republic", "Germany", "Denmark", "Estonia", "Spain",
"Finland", "France", "United Kingdom", "Hungary", "Ireland",
"Israel", "Iceland", "Italy", "Lithuania", "Netherlands", "Norway",
"Poland", "Portugal", "Russia", "Sweden", "Slovenia", "Slovakia",
"Ukraine", "Kosovo")
colnames(cntry.human.values) <- sub(srv.variables[J(human.values)][,title],
pattern = "Important to |Important that ", replacement = "")
И выполняем факторизацию неотрицательных матриц ранга 5
nmf.fit <- nmf(cntry.human.values, 5, method = "brunet", seed=123456, nrun=100)
Теперь строим теплокарты матриц W и H. Они определяют разложение исследуемых характеристик в пространстве 5 латентных переменных. Чем темнее клетка, тем более выражено соответствие между латентной переменной и ценностью или страной. Я опускаю математические детали точного определения, подробности можно найти в [1].
Далее отбираем лишь те human.values переменные, которые выражены только по одной из осей в этом пространстве. Названия осей даны мной самостоятельно.
Построение карты профилей
nmf.selected <- nmf.fit[, c(2, 7:10, 13, 15, 21)]
basismap(t(nmf.selected), tracks=NA, main="Latent variables: Profiles explanation",
scale = "r1", legend = NA, Rowv=TRUE, labCol = c("money | success",
"have good time", "be humble & modest", "advantures | fun", "rules | understanding"))

Ниже показан итоговый результат — представление всех 29 стран. Цветом выражены степени соответствия переменных. К тому же страны группируются следуя иерархической кластеризации с евклидовой метрикой в 5-мерном пространстве латентных переменных.
Скрытый текст
basismap(nmf.selected, tracks=NA, main=«Countries in the latent variables space»,
legend = NA, labCol = c(«money | success», «have good time», «be humble & modest»,
«advantures | fun», «rules | understanding»))
legend = NA, labCol = c(«money | success», «have good time», «be humble & modest»,
«advantures | fun», «rules | understanding»))

Видим, что в этом пространстве наиболее близкая страна к России — Словакия. Эти страны, в частности, выделяются выраженностью по первой оси, чего нельзя сказать, например, о Франции. Подробнее этот момент будет рассмотрен в следующей части статьи. Диаграмма также показывает какие страны составляют кластеры, в зависимости от требуемой подробности. Например, кластер из стран восточной Европы (Словакия, Россия, Чехия, Украина, Болгария, Венгрия, Литва) и Израиля. Любопытный кластер из Албании, Косово и… Польши. А Норвегия с Финляндией достаточно далеко расположены от Дании со Швецией.
Сравнение с результатами анализа соответствий
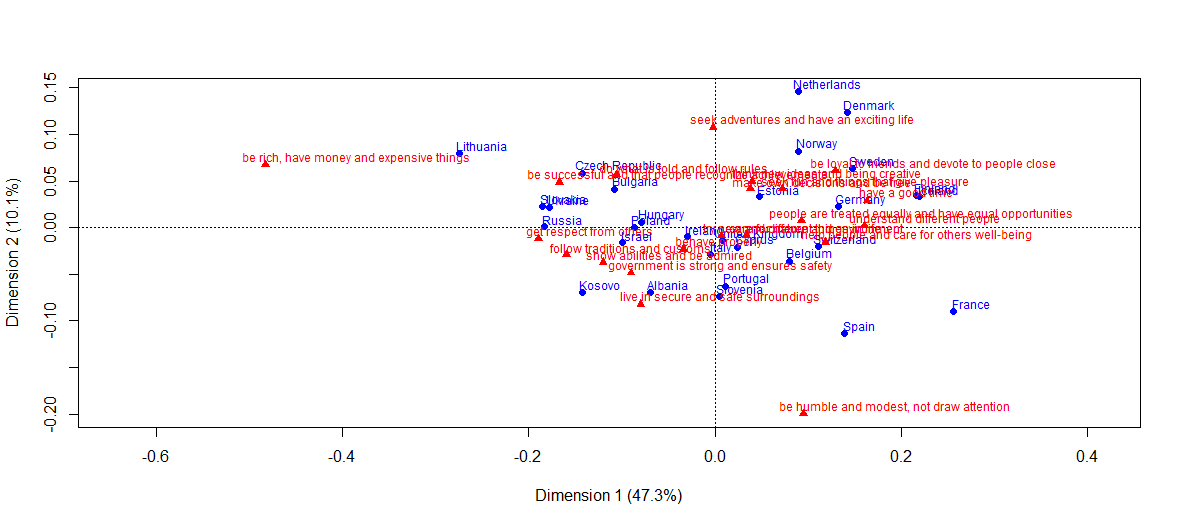
Какие преимущества у NMF?
— В отличии от NMF, в графическом представлении классического анализа соответствий используются только два собственных значения (на графике выше кумулятивная инерция осей CA равна 57.4 %). В NMF визуализация наглядна и для ранга большего двух.
— Во-вторых, теплокарты представляют информацию более структурировано и наглядно, нежели плоскость CA.
library(ca)
plot(ca(cntry.human.values), what=c("all", "active"))

Какие преимущества у NMF?
— В отличии от NMF, в графическом представлении классического анализа соответствий используются только два собственных значения (на графике выше кумулятивная инерция осей CA равна 57.4 %). В NMF визуализация наглядна и для ранга большего двух.
— Во-вторых, теплокарты представляют информацию более структурировано и наглядно, нежели плоскость CA.
С применением NMF для маркетинговой таблицы сопряженности можно познакомиться в этой публикации. В ней рассмотрен пример анализа восприятия 14 автомобильных марок.
Диаграммы NMF, на сколько хороши бы они не были, в общем случае, не дают оснований делать доказательные выводы о сходствах и различиях разных стран относительно представлений о ценностях. Эта задача будет рассмотрена в следующей части статьи.
Литература:
[1] Renaud Gaujoux et al. A flexible R package for nonnegative matrix factorization. In: BMC Bioinformatics 11.1 (2010), p. 367.


Arbuz
Спасибо за статью.
Поясните, пожалуйста, как произошёл переход к латентным переменным.
Или это «наиболее важные» из всех, полученные в результате факторизации?
Arbuz
Перечитал вторую статью, осознал, что мой вопрос задан не вполне корректно.
Переформулирую: почему переменные «латентные», ведь они наблюдались непосредственно?
barmaley_exe
Матрицы W и H были получены с помощью разложения и явно не наблюдались. Наблюдался лишь результат их перемножения.
jzha
Спасибо за вопрос. Я не знаю точного названия этих переменных. Вероятно, еще нет устоявшегося термина.
Как справедливо ответили ниже, эти переменные явно не наблюдались. Названия «money | success», «have good time»,… даны мной для упрощения. На самом деле вид этих «латентных» переменных сложнее. Упомянутые наблюдаемые логические переменные представлены наиболее значимо только на одной из этих осей (обратите внимание на опцию scale = «r1», для построения карты t(nmf.selected), детали можно найти в документации пакета). Поэтому да, выделенные 8 наблюдаемых переменных, с точки зрения поставленной задачи, «наиболее важные» составляющие 5 латентных переменных.