В предыдущей части публикации был рассмотрен метод факторизации неотрицательных матриц в качестве снижения размерности и визуализации таблиц сопряженности. В этой части будет проведен статистический анализ полученных диаграмм с использованием лог-линейных моделей. Напомню, примеры демонстрируются для complex survey данных — стратифицированных, кластеризованных и взвешенных выборок. Это обстоятельство предполагает применение специальных методов оценки и выбора моделей. Для визуализации полученных результатов применяются Марковские сети — удобный инструмент графического представления взаимодействия факторов лог-линейных моделей.

Кратко о предыдущей серии. По ESS данным 2012 года для генеральной совокупности “Мужчины возраста 25-40 лет” была построена таблица о степени поддержки человеческих ценностей в каждой из стран опроса. Для понижения размерности представления матрицы размера 29х21, определяемой таблицей, было произведено NMF преобразование ранга 5. Повторю итоговую теплокарту позиционирования всех 29 стран в полученном пространстве, чтобы она была перед глазами

Постановка задачи
Построенная карта подсказывает между какими странами (или кластерами стран) гипотеза о независимости распределения долей ценностных переменных от стран (кластеров стран) может быть отклонена. Требуется статистически подтвердить возникающие гипотезы. Для примеров будем использовать следующие группы стран
Разумеется выбор не ограничивается только этими примерами и исследователь может выбрать те страны или кластеры стран, совпадающие с его интересами.
Помимо проверки гипотез возникает вопрос — как взаимодействуют ценностные факторы в зависимости от группы выбранных стран? Требуется выявить эти возможные различия.
Немного о таблицах сопряженности
Все ценностные переменные в таблице для выполнения NMF преобразования воспринимались как одна переменная со множественным выбором (multiple response variable). Это было необходимо для представления данных в виде двухмерной таблицы, то есть таблицы образованной двумя переменными. В действительности у нас ситуация несколько иная, полный набор из 21 ценностной переменной и 1 переменная указывающая страну определяют 22-мерную таблицу сопряженности.
Вероятно это покажется удивительным, но с точки зрения построения статистических моделей, многомерные таблицы сопряженности (c single response переменными и без пропущенных ответов) — более простая ситуация, нежели таблицы с multiple response переменными. Кроме того, с помощью NMF размерность таблицы была снижена до 6 — 5 латентных переменных + 1 переменная со страной.
Лог-линейные модели
Классический метод анализа многомерной таблицы сопряженности — построение ее лог-линейной модели. Лог-линейный анализ можно воспринимать как обобщение хи-квадрат критерия на случай многомерных таблиц. Определение лог-линейных моделей можно посмотреть в Википедии (eng). По этой теме доступны материалы с примерами на русском языке, например, здесь или здесь, а также детальные лекции на английском языке здесь.
Прежде чем перейти к вычислениям отметим, что в общем случае многомерные таблицы сопряженности определяют мультиномиальное распределение. Но когда маргинальные суммы этого распределения по одному измерению или нескольким измерениям фиксированы, получаем так называемое product-multinomial распределение. Поэтому требуется накладывать дополнительные ограничения на параметры лог-линейных моделей для таких таблиц. Подробности можно найти в главе 12 книги [1]. В нашем случае маргинальные суммы фиксируются по одному измерению — размеры генеральных совокупностей в каждой из стран являются константами. Это означает, что главный эффект отвечающий переменной со страной не может быть исключен из модели.
Последнее замечание. Мы опустим вопрос о том, какие таблицы для survey данных считаются разреженными и, как следствие, не будем проводить соответствующие проверки.
Определяем и сравниваем модели
По-прежнему используем пакет survey [2] среды R для учета эффектов стратификации, кластеризации и взвешивания выборки. Более подробно об этом сообщалось в одной из прошлых публикаций. Параметры лог-линейных моделей для complex survey данных ровно те же самые, что и для таблиц без учета дизайна исследования. Требуется корректировка формул вычисляющих значимость параметров модели (как в отдельности, так и в совокупности).
Пример 1, простейший — таблица для России и Словакии с одной латентной переменной «money | success».

Строим две модели: предполагающую независимость факторов и насыщенную.
что насыщенная модель не является значимо лучшей по сравнению с моделью, предполагающей независимость.
То есть, мы не можем отвергнуть нулевую гипотезу о независимости переменных в таблице.
Для сравнения это таблица с результатами независимой модели

Пример 2. Рассмотрим таблицу со всеми пятью латентными переменными для Франции и России.
Лог-линейная модель, предполагающая попарную независимость всех факторов отвергается. Модель со всеми элементами второго порядка является приемлемой. Эту модель можно (и нужно) упростить — отбросить по результатам wald и likelihood ratio критериев, параметры второго порядка для переменной определяющей страну и последними двумя латентными переменными теплокарты.
Условная независимость. Почему математические способности и размер обуви — зависимые факторы?
Эта вариация на тему классического примера. Предположим, математические способности респондента определяются следующей градацией--- высокие, средние или низкие. Строим таблицу сопряженности с этими двумя переменными, скажем, для населения всей России. Гипотеза о независимости этих переменных смело может быть отвергнута. У людей с большим размером обуви выше математические способности. В чем причина? В отсутствии скрытой переменной — возраст. Ясно, что до определенного момента возраст положительно коррелирует как с математическими способностями, так и с размером обуви. Если фиксировать возраст (Age = k), то для любого k таблица совместного распределения величин M (мат. способности) и S (размер обуви) не будет указывать о наличии значимой зависимости между ними. В таком случае говорят, что величины M и S условно независимы. Этот результат выражается естественным образом в виде Марковской сети — ненаправленной графической модели.
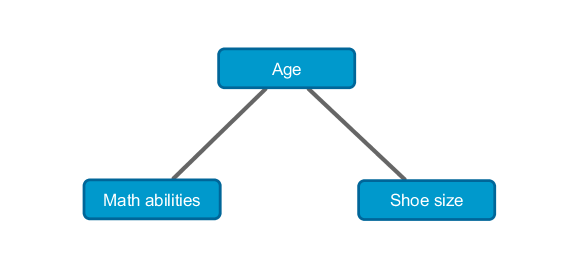
Добавлю, что на Хабре есть отличная статья о Байесовских сетях — направленных графических моделях.
Графическое представление лог-линейных моделей
Предыдущий пример можно обобщить и распространить его на произвольные иерархические лог-линейные модели, что и было реализовано в работе [3]. Рассмотрим ряд возможных вариантов для трех переменных A, B и C.
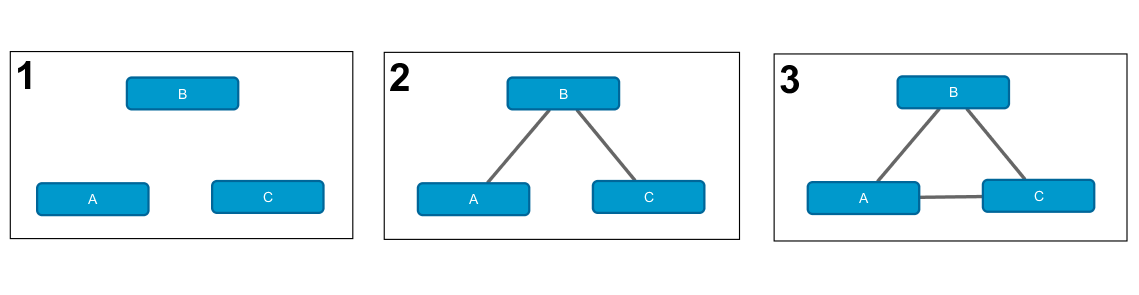
Эти Марковские сети соответствуют следующим лог-линейным моделям
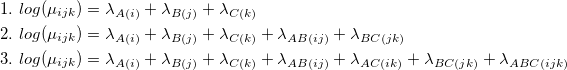
Заметим, что не всякая иерархическая лог-линейная модель может быть представлена в виде Марковской сети. Например — модель AB/AC/BC. Но любая модель может быть однозначно вложена в минимальную Марковскую сеть. Подробности соответствия лог-линейных и графических моделей можно найти в книге [1] или статье [3].
Итоговые результаты
Марковские сети позволяют относительно легко ориентироваться во взаимоотношениях переменных и сравнивать результаты различных таблиц.


Видим, что в случае России и Словакии наблюдается значимая взаимосвязь между страной и переменной «важен поиск приключений и риск или возможность повеселиться». С остальными ценностными качествами переменная Country условна независима.
Тогда как во Франции и России значимо различие в отношении к трем утверждениям: «важно быть богатым или иметь успех», «важно хорошо проводить время» и «важно быть простым и скромным».
Оба этих вывода согласуются с результатами теплокарты.
Что же касается взаимосвязи между латентными переменными, то графы для этих пар стран отличаются только одним ребром. Для России и Словакии переменные «важно хорошо проводить время» и «важно следовать правилам или важно помогать окружающим» условно независимы.
В заключение отмечу, что в лог-линейных моделях для complex survey данных пошаговый выбор модели, основанный на AIC или BIC результатах, пока не реализован. Статьи с адаптацией этих критериев к таким данным стали появляться только в последние годы. В частности, в этом году вышла статья [4], один из соавторов которой — T. Lumley, создатель пакета survey.
Литература:
[1] G. Tutz (2011) Regression for Categorical Data, Cambridge University Press.
[2] T. Lumley (2014) survey: analysis of complex survey samples. R package version 3.30.
[3] J. N. Darroch, S. L. Lauritzen, and T. P. Speed (1980) Markov fields and log-linear interaction models for contingency tables. Annals of Statistics 8(3), 522–539.
[4] T. Lumley, A. Scott (2015) AIC and BIC for modelling with complex survey data, J. Surv. Stat. Method. 3 (1), 1-18.

Кратко о предыдущей серии. По ESS данным 2012 года для генеральной совокупности “Мужчины возраста 25-40 лет” была построена таблица о степени поддержки человеческих ценностей в каждой из стран опроса. Для понижения размерности представления матрицы размера 29х21, определяемой таблицей, было произведено NMF преобразование ранга 5. Повторю итоговую теплокарту позиционирования всех 29 стран в полученном пространстве, чтобы она была перед глазами

Постановка задачи
Построенная карта подсказывает между какими странами (или кластерами стран) гипотеза о независимости распределения долей ценностных переменных от стран (кластеров стран) может быть отклонена. Требуется статистически подтвердить возникающие гипотезы. Для примеров будем использовать следующие группы стран
- Россия и Словакия, по результатам иерархической кластеризации — соседи;
- Франция и Россия, как варианты стран с различными представлениями.
Разумеется выбор не ограничивается только этими примерами и исследователь может выбрать те страны или кластеры стран, совпадающие с его интересами.
Помимо проверки гипотез возникает вопрос — как взаимодействуют ценностные факторы в зависимости от группы выбранных стран? Требуется выявить эти возможные различия.
Немного о таблицах сопряженности
Все ценностные переменные в таблице для выполнения NMF преобразования воспринимались как одна переменная со множественным выбором (multiple response variable). Это было необходимо для представления данных в виде двухмерной таблицы, то есть таблицы образованной двумя переменными. В действительности у нас ситуация несколько иная, полный набор из 21 ценностной переменной и 1 переменная указывающая страну определяют 22-мерную таблицу сопряженности.
Вероятно это покажется удивительным, но с точки зрения построения статистических моделей, многомерные таблицы сопряженности (c single response переменными и без пропущенных ответов) — более простая ситуация, нежели таблицы с multiple response переменными. Кроме того, с помощью NMF размерность таблицы была снижена до 6 — 5 латентных переменных + 1 переменная со страной.
Лог-линейные модели
Классический метод анализа многомерной таблицы сопряженности — построение ее лог-линейной модели. Лог-линейный анализ можно воспринимать как обобщение хи-квадрат критерия на случай многомерных таблиц. Определение лог-линейных моделей можно посмотреть в Википедии (eng). По этой теме доступны материалы с примерами на русском языке, например, здесь или здесь, а также детальные лекции на английском языке здесь.
Прежде чем перейти к вычислениям отметим, что в общем случае многомерные таблицы сопряженности определяют мультиномиальное распределение. Но когда маргинальные суммы этого распределения по одному измерению или нескольким измерениям фиксированы, получаем так называемое product-multinomial распределение. Поэтому требуется накладывать дополнительные ограничения на параметры лог-линейных моделей для таких таблиц. Подробности можно найти в главе 12 книги [1]. В нашем случае маргинальные суммы фиксируются по одному измерению — размеры генеральных совокупностей в каждой из стран являются константами. Это означает, что главный эффект отвечающий переменной со страной не может быть исключен из модели.
Последнее замечание. Мы опустим вопрос о том, какие таблицы для survey данных считаются разреженными и, как следствие, не будем проводить соответствующие проверки.
Определяем и сравниваем модели
По-прежнему используем пакет survey [2] среды R для учета эффектов стратификации, кластеризации и взвешивания выборки. Более подробно об этом сообщалось в одной из прошлых публикаций. Параметры лог-линейных моделей для complex survey данных ровно те же самые, что и для таблиц без учета дизайна исследования. Требуется корректировка формул вычисляющих значимость параметров модели (как в отдельности, так и в совокупности).
Загружаем данные, выделяем ген. совокупность, добавляем в базу латентные переменные и задаем дизайн исследования.
library(foreign)
library(data.table)
library(survey)
srv.data <- read.dta("ESS6e02_1.dta")
srv.variables <- data.table(name = names(srv.data), title = attr(srv.data, "var.labels"))
srv.data <- data.table(srv.data)
setkey(srv.data, cntry)
setkey(srv.variables, name)
fr.dt<-data.table(read.dta("ESS6_FR_SDDF.dta"))
ru.dt<-data.table(read.dta("ESS6_RU_SDDF.dta"))
ru.dt[,psu:=psu+150] # psu values are changed to avoid their intersections between countries
sk.dt<-data.table(read.dta("ESS6_SK_SDDF.dta"))
sddf.data <- rbind(fr.dt, ru.dt, sk.dt)
setkey(sddf.data, cntry, idno)
cntries.data <- srv.data[J(c("FR", "RU", "SK"))]
cntries.data[ ,weight:=dweight*pweight]
setkey(cntries.data, cntry, idno )
cntries.data <- cntries.data[sddf.data]
cntries.data <- cntries.data[gndr == 'Male' & agea >= 25 & agea<=40, ]
# add the latent variables<b> a.1, a.2, ..., a.5</b> to the cntries.data
answers <- c('Very much like me', 'Like me')
cntries.data[,a.1:= imprich %in% answers | ipsuces %in% answers]
cntries.data[,a.2:= ipgdtim %in% answers]
cntries.data[,a.3:= ipmodst %in% answers]
cntries.data[,a.4:= ipadvnt %in% answers | impfun %in% answers]
cntries.data[,a.5:= ipfrule %in% answers | ipudrst %in% answers]
# define survey design
srv.design.data <- svydesign(ids = ~psu, strata = ~stratify, weights = ~weight, data = cntries.data)
options(survey.lonely.psu="adjust")
Пример 1, простейший — таблица для России и Словакии с одной латентной переменной «money | success».

Строим две модели: предполагающую независимость факторов и насыщенную.
Вычисления показывают ...
Analysis of Deviance Table
Model 1: y ~ a.1 + cntry
Model 2: y ~ a.1 + cntry + a.1:cntry
Deviance= 0.1240613 p= 0.4737981
Score= 0.1217862 p= 0.4778766
ru.sk.data <- subset(srv.design.data, cntry %in% c("RU", "SK"))
srv.loglin.model.ind <- svyloglin(~a.1+cntry, ru.sk.data)
srv.loglin.model.sq <- update(srv.loglin.model.ind, ~.^2)
anova(srv.loglin.model.ind, srv.loglin.model.sq)
Analysis of Deviance Table
Model 1: y ~ a.1 + cntry
Model 2: y ~ a.1 + cntry + a.1:cntry
Deviance= 0.1240613 p= 0.4737981
Score= 0.1217862 p= 0.4778766
что насыщенная модель не является значимо лучшей по сравнению с моделью, предполагающей независимость.
То есть, мы не можем отвергнуть нулевую гипотезу о независимости переменных в таблице.
Для сравнения это таблица с результатами независимой модели

Пример 2. Рассмотрим таблицу со всеми пятью латентными переменными для Франции и России.
Лог-линейная модель, предполагающая попарную независимость всех факторов отвергается. Модель со всеми элементами второго порядка является приемлемой. Эту модель можно (и нужно) упростить — отбросить по результатам wald и likelihood ratio критериев, параметры второго порядка для переменной определяющей страну и последними двумя латентными переменными теплокарты.
Вычисления
cntry:a.1 cntry:a.2 cntry:a.3 cntry:a.4 cntry:a.5
0.000 0.000 0.000 0.437 0.524
0.6066181
fr.ru.data <- subset(srv.design.data, cntry %in% c("FR", "RU"))
srv.loglin.model.ind <- svyloglin(~ a.1 + a.2 + a.3 + a.4 + a.5 + cntry, fr.ru.data)
srv.loglin.model.sq <- update(srv.loglin.model.ind, ~.^2)
srv.loglin.model.tri <- update(srv.loglin.model.ind, ~.^3)
srv.loglin.model.four <- update(srv.loglin.model.ind, ~.^4)
anova(srv.loglin.model.ind, srv.loglin.model.sq)$dev$p[3] #5.745843e-50
c( anova(srv.loglin.model.sq, srv.loglin.model.tri), anova(srv.loglin.model.sq, srv.loglin.model.four) ) # 0.7335668 0.7427429
sapply(paste('cntry:a.',1:5,sep=""), function(x) round(regTermTest(srv.loglin.model.sq, x)$p, 3) )
cntry:a.1 cntry:a.2 cntry:a.3 cntry:a.4 cntry:a.5
0.000 0.000 0.000 0.437 0.524
anova(update(srv.loglin.model.sq, ~. -cntry:(a.4 + a.5)), srv.loglin.model.sq)$dev$p[3]
0.6066181
Условная независимость. Почему математические способности и размер обуви — зависимые факторы?
Эта вариация на тему классического примера. Предположим, математические способности респондента определяются следующей градацией--- высокие, средние или низкие. Строим таблицу сопряженности с этими двумя переменными, скажем, для населения всей России. Гипотеза о независимости этих переменных смело может быть отвергнута. У людей с большим размером обуви выше математические способности. В чем причина? В отсутствии скрытой переменной — возраст. Ясно, что до определенного момента возраст положительно коррелирует как с математическими способностями, так и с размером обуви. Если фиксировать возраст (Age = k), то для любого k таблица совместного распределения величин M (мат. способности) и S (размер обуви) не будет указывать о наличии значимой зависимости между ними. В таком случае говорят, что величины M и S условно независимы. Этот результат выражается естественным образом в виде Марковской сети — ненаправленной графической модели.

Добавлю, что на Хабре есть отличная статья о Байесовских сетях — направленных графических моделях.
Графическое представление лог-линейных моделей
Предыдущий пример можно обобщить и распространить его на произвольные иерархические лог-линейные модели, что и было реализовано в работе [3]. Рассмотрим ряд возможных вариантов для трех переменных A, B и C.

Эти Марковские сети соответствуют следующим лог-линейным моделям
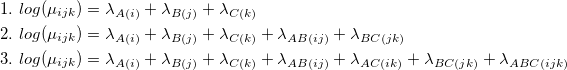
Заметим, что не всякая иерархическая лог-линейная модель может быть представлена в виде Марковской сети. Например — модель AB/AC/BC. Но любая модель может быть однозначно вложена в минимальную Марковскую сеть. Подробности соответствия лог-линейных и графических моделей можно найти в книге [1] или статье [3].
Итоговые результаты
Марковские сети позволяют относительно легко ориентироваться во взаимоотношениях переменных и сравнивать результаты различных таблиц.


Видим, что в случае России и Словакии наблюдается значимая взаимосвязь между страной и переменной «важен поиск приключений и риск или возможность повеселиться». С остальными ценностными качествами переменная Country условна независима.
Тогда как во Франции и России значимо различие в отношении к трем утверждениям: «важно быть богатым или иметь успех», «важно хорошо проводить время» и «важно быть простым и скромным».
Оба этих вывода согласуются с результатами теплокарты.
Что же касается взаимосвязи между латентными переменными, то графы для этих пар стран отличаются только одним ребром. Для России и Словакии переменные «важно хорошо проводить время» и «важно следовать правилам или важно помогать окружающим» условно независимы.
В заключение отмечу, что в лог-линейных моделях для complex survey данных пошаговый выбор модели, основанный на AIC или BIC результатах, пока не реализован. Статьи с адаптацией этих критериев к таким данным стали появляться только в последние годы. В частности, в этом году вышла статья [4], один из соавторов которой — T. Lumley, создатель пакета survey.
Литература:
[1] G. Tutz (2011) Regression for Categorical Data, Cambridge University Press.
[2] T. Lumley (2014) survey: analysis of complex survey samples. R package version 3.30.
[3] J. N. Darroch, S. L. Lauritzen, and T. P. Speed (1980) Markov fields and log-linear interaction models for contingency tables. Annals of Statistics 8(3), 522–539.
[4] T. Lumley, A. Scott (2015) AIC and BIC for modelling with complex survey data, J. Surv. Stat. Method. 3 (1), 1-18.

