22.01.2020 12:14
Serine 28 12200 Источник

image


Как быть, если дерево поиска разрослось на всю оперативку и вот-вот подопрет корнями соседние стойки в серверной? Что делать с инвертированным индексом, жадным до ресурсов? Завязывать ли с разработкой под Android, если пользователю прилетает «Память телефона заполнена», а приложение едва на половине загрузки важного контейнера?


В целом, можно ли сжать структуру данных, чтобы она занимала заметно меньше места, но не теряла присущих ей достоинств? Чтобы доступ к хэш-таблице оставался быстрым, а сбалансированное дерево сохраняло свои свойства. Да, можно! Для этого и появилось направление информатики «Succinct data structures», исследующее компактное представление структур данных. Оно развивается с конца 80-х годов и прямо сейчас переживает расцвет в лучах славы big data и highload.


А тем временем на Хабре найдется ли герой, способный пересковоговорить три раза подряд
[s?k?s??kt]?


Дверь в мир компактности


Итак, структура данных считается компактной (succinct), если она:


  • Занимает количество бит, близкое к информационно-теоретической нижней границе.
  • Не требует предварительной распаковки для полноценного использования.

Это означает, что алгоритмы сжатия без потерь никакого отношения к компактным структурам данных не имеют. Ведь они предполагают восстановление данных из сжатого состояния для их обработки.


Привычные, «мейнстримовые» реализации графов, хэш-таблиц и прочего тоже не годятся. Взять хотя бы указатели на дочерние элементы в дереве поиска. Они отъедают порядочно места: $O(MN)$, где $M$ — длина указателя, а $N$ — количество узлов в дереве. Зато succinct реализация дерева позволяет улучшить асимптотику до $2N + o(N)$, что близко к теоретической нижней границе $2N ? ?(log N)$ для дерева из $N$ узлов. При длине указателя $M=8$ байт это означает переход от $O(8N)$ к совершенно другому порядку асимптотики — всего лишь $2N$, если учитывать, что $o(N)$ — пренебрежимо малая величина относительно $N$.


Компактные (succinct) структуры данных — это сжатые представления для битовых векторов, мультимножеств, планарных графов и других всеми любимых классических структур. Зачастую они статические, построенные единожды и не меняющиеся в процессе использования. Есть и исключения — succinct-структуры с быстрыми операциями добавления и удаления элементов.


В основе большинства компактных структур лежит концепция так называемого компактного индексируемого словаря. Это — частный случай битовой карты (bitmap, bitset). Сама по себе битовая карта идеальна для проверки вхождения элементов в некое множество. Если элемент включен в множество, то значение бита по заданному индексу устанавливается в 1, если нет — сбрасывается в 0. Жизненный пример — inode-битмапа ext4, UFS и других юниксовых файловых систем. Она хранит данные о том, какие записи в таблице индексных дескрипторов заняты, а какие — свободны.


Компактный индексируемый словарь — это та же битовая карта, но дополненная двумя операциями: rank и select. Эти операции — слоны, на которых зиждется мир succinct. Грубо говоря, rank — это подсчет количества элементов, а select — поиск элемента:


  • $rank_x(i)$ возвращает количество бит, равных $x$, чьи индексы лежат на отрезке $[0; i]$. Так как $x$ — значение бита, то он может быть равен исключительно 0 или 1.
  • $select_x(j)$ возвращает индекс $j$-го бита, равного $x$. Здравый смысл говорит, что нулевого вхождения не бывает, есть только первое. Поэтому $inline$j > 0$inline$: подсчет ведется от единицы. Кроме того, $j$ не может превышать суммарное количество битов в словаре, равных $x$.

Допустим, у нас есть индексируемый словарь, в котором 4 из 7 бит установлены. Тогда $rank_1$ и $select_1$ примут следующие значения:



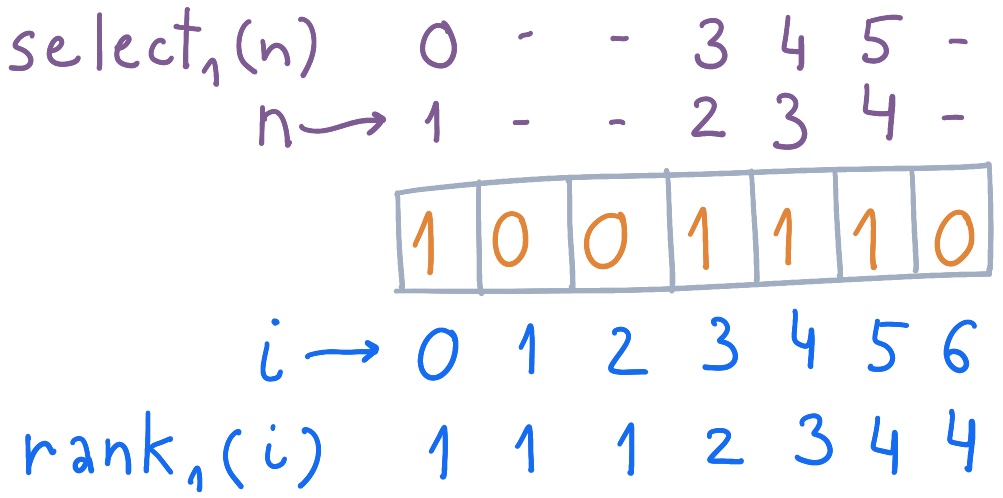
Пример индексируемого словаря и расчета для него $rank_1$, $select_1$.


Внимательный читатель заметит, что select — обратная операция для rank. Если $rank_1(5) = 4$, то $select_1(4)=5$.


У кого-нибудь возникло дежавю при виде $rank_1(i)$? А все потому, что эта операция обобщает Вес Хэмминга — количество ненулевых символов в последовательности. Применительно к бинарным последовательностям Вес Хэмминга также называется popcount (population count).


Rank/select применимы и для сброшенных битов. Вот пример расчета $rank_0$ и $select_0$ для битов, равных 0:



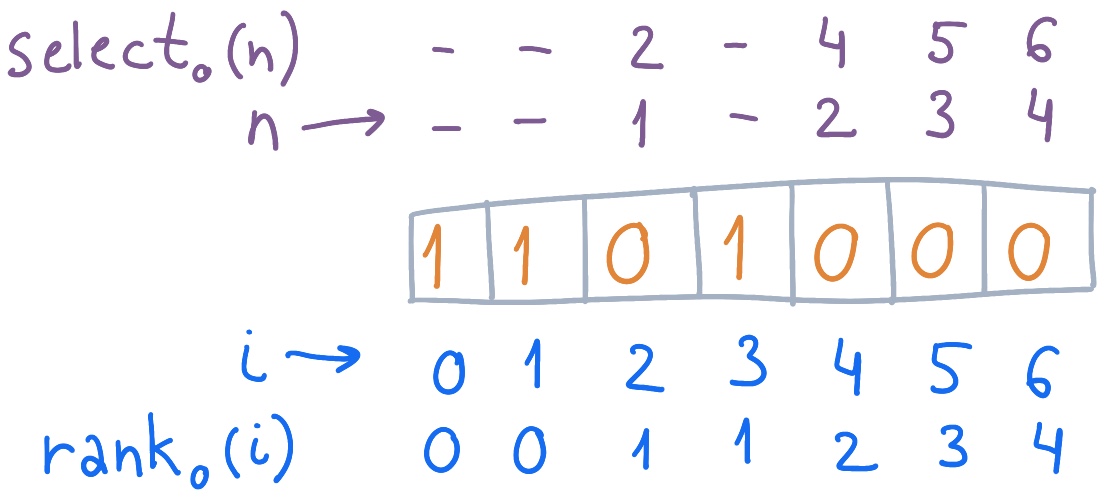
Пример компактного индексируемого словаря и расчета для него $rank_0$, $select_0$.


Распилить дерево на битики


Используем же это знание, чтобы построить компактное префиксное дерево! Префиксные деревья хороши для поиска строк по префиксу. С их помощью зачастую реализуется выпадающий список поисковых подсказок (саджест). Подход к succinct'изации префиксного дерева предельно обобщенный и по максимуму демонстрирует весь изюм компактных структур. В отличие от бинарного дерева, для которого выведены частные формулы, мешающие увидеть общую картину.


Популярнее всего три метода компактного представления деревьев:


  • BP (balanced parentheses) — сбалансированные скобочные последовательности.
  • DFUDS (depth-first unary degree sequence) — последовательности единично-закодированных узлов, сортированных поиском в глубину.
  • LOUDS (level-ordered unary degree sequences) — последовательности единично-закодированных узлов, сортированных по уровням.

Что за подозрительная логическая цепочка перевода «unary degree» в «единично-закодированный узел»? Что ж. Unary degree в этих названиях означает способ кодирования узлов дерева последовательностью единиц по количеству дочерних узлов, обязательно с нулем в прицепе.


Эти три метода представления деревьев объединяет наличие быстрых операций: найти родителя; найти первого потомка; найти последнего потомка; найти левый и правый соседние узлы. Принципиальная возможность и эффективность других операций отличаются от метода к методу.


Остановимся на методе LOUDS. Поняв его, не составит труда разобраться с двумя другими. К тому же, в прошлом году LOUDS-деревья отметили свой 30-й день рождения! Дополнительные полезные операции для LOUDS-деревьев реализуются за $O(1)$: найти количество потомков узла; вычислить номер потомка узла среди всех его потомков (первый потомок, второй, $i$-ый и т.д.); найти $i$-ого потомка. Недостаток LOUDS — отсутствие эффективного алгоритма подсчета количества узлов поддерева.


Суть метода проста: хранить ключи узлов дерева и всю ценную информацию в обычном массиве, а структуру дерева представить как последовательность бит. Итого имеем две статические структуры. Зато не нужно выделять память под указатели на узлы дерева: переходы между ними реализованы по формулам с активным применением rank/select.


Внимание, префиксное дерево:



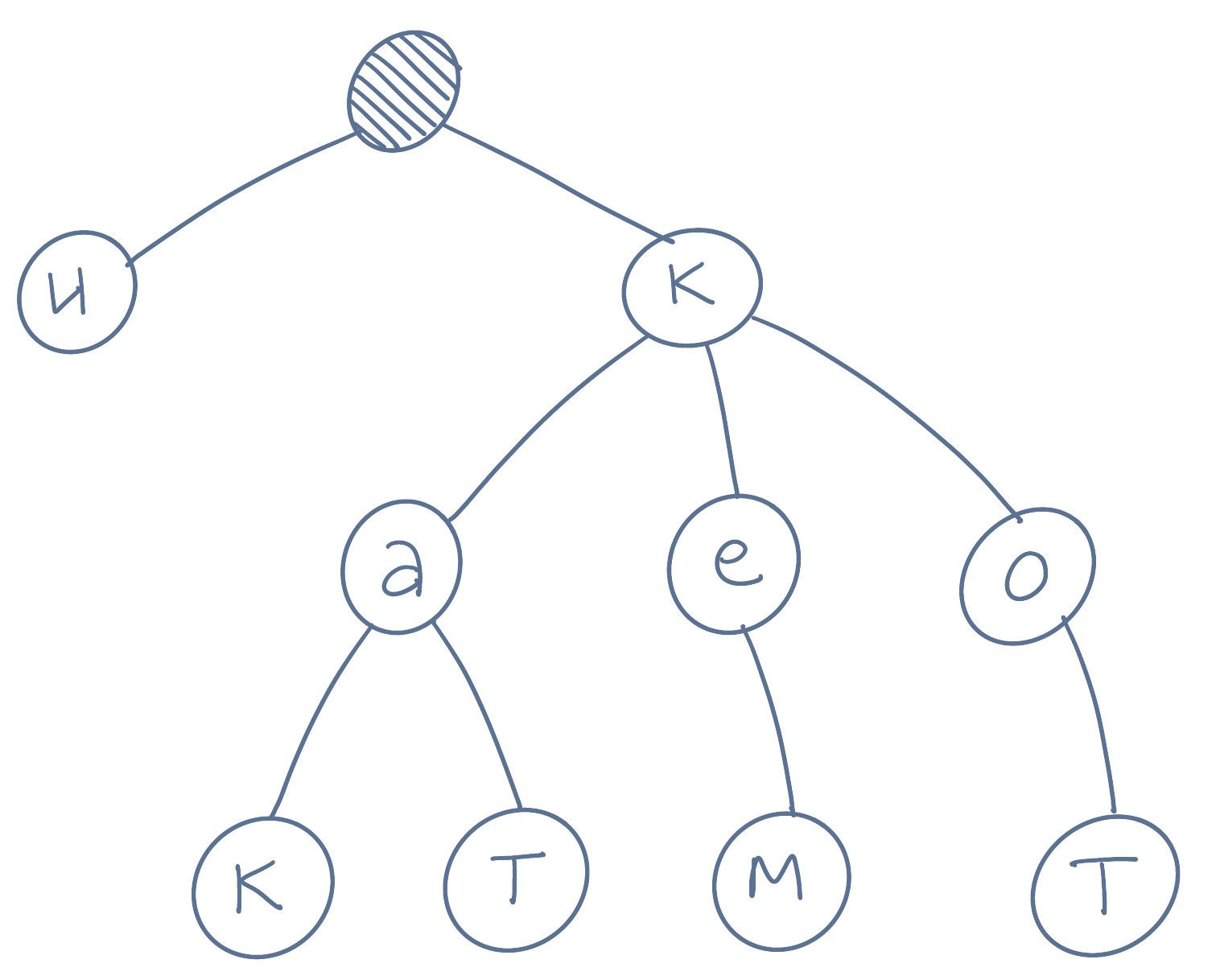
Префиксное дерево, готовое к сжатию методом LOUDS.


Подготовим дерево к представлению в бинарном виде:


  1. Прикрепим дерево к фейковому корню. Он сыграет свою роль совсем скоро.
  2. Пронумеруем все узлы дерева уровень за уровнем слева направо, как при BFS (поиске в ширину). Фейковый корень игнорируется, а настоящий индексируется нулем.
  3. Закодируем узлы. Узел дерева кодируется последовательностью единиц, соответствующим прямым потомкам, плюс ноль. Если у узла четыре дочерних элемента, то он кодируется как 11110, а если ни одного — как 0. Фейковый корень кодируется в первую очередь. У него единственный потомок, поэтому его код 10.


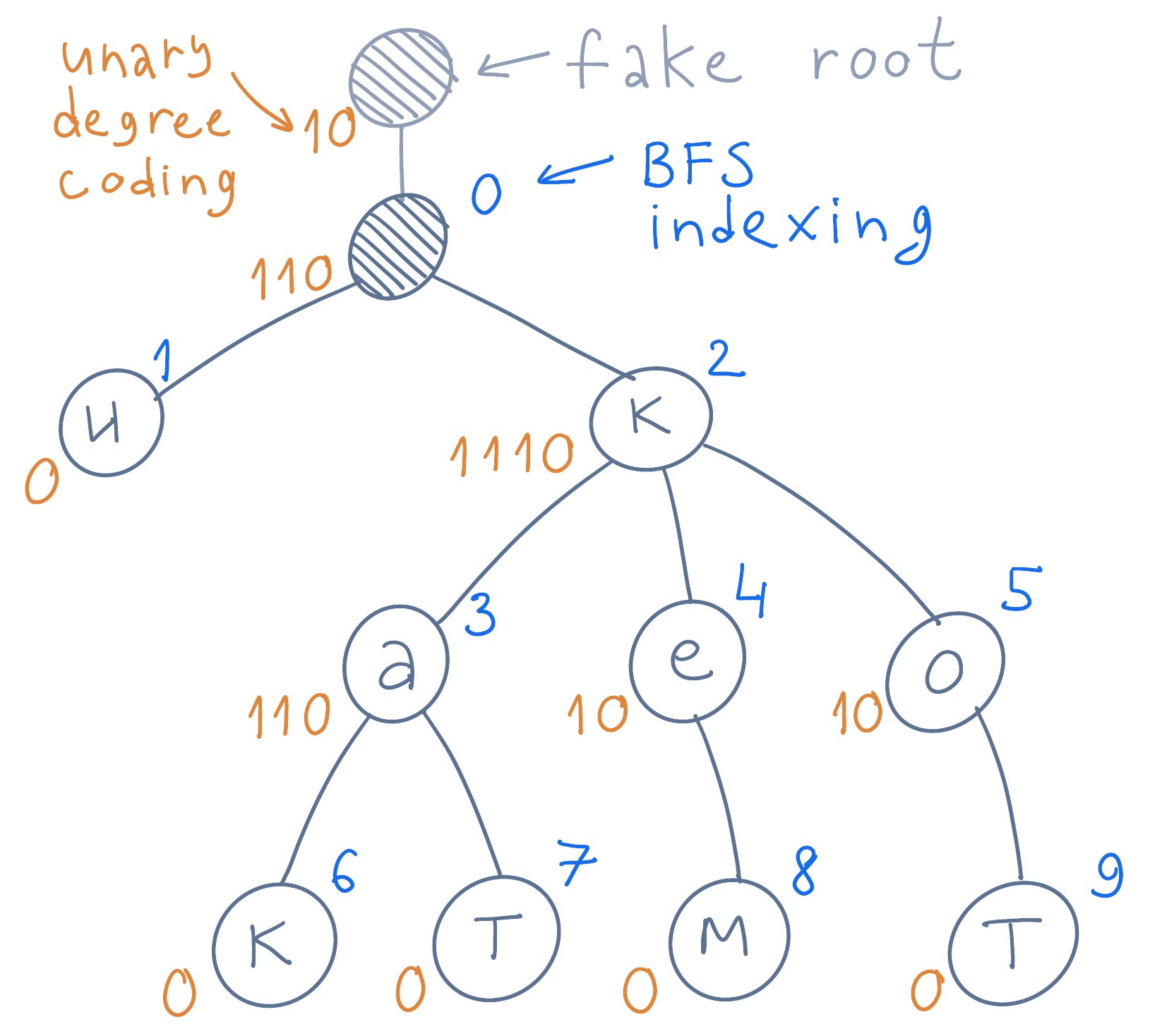
Префиксное дерево с пронумерованными по уровням узлами. Узлы закодированы.


В процессе поуровневого обхода дерева формируется компактный индексируемый словарь — последовательность бит из склеенных сверху вниз и слева направо закодированных узлов. У нас это 21-битная последовательность. Кстати, она называется LBS (LOUDS Bit String).



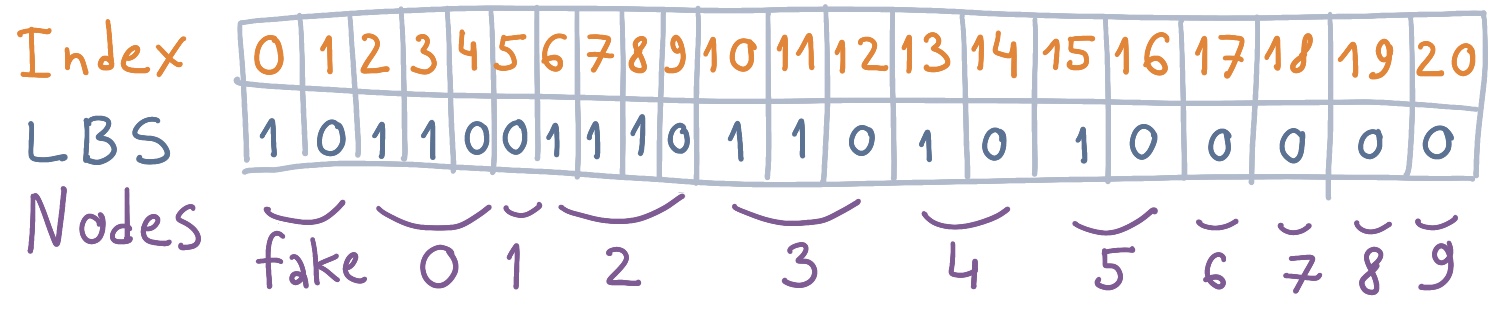
Компактный индексируемый словарь для префиксного дерева.


Компактное префиксное дерево LOUDS построено. LBS для дерева с $N$ узлами (фейковый не в счет) занимает $2N+1$ бит. Осталось самое интересное — формулы для обхода дерева, превращенного в битовую карту.


Поиск первого потомка. Переход от узла $i$ к его первому дочернему узлу осуществляется по формуле:


$firstChild(i)= select_0(i + 1) - i$


$i$ — это номер узла, в предыдущей табличке проставленный фиолетовым.


Найдем первого потомка узла с индексом 3 (буква «а»):


$firstСhild(3) = select_0(3+1) - 3 = select_0(4) - 3 = 9 - 3 = 6$


Первый дочерний узел находится по индексу 6, и это буква «к». Применим формулу для корня дерева:


$firstChild(0) = select_0(0+1) - 0 = select_0(1) = 1$


Мы нашли лист с индексом 1, букву «и». Сходится! Стало ясно, зачем потребовался фейковый корень: для магии индексации узлов. Во избежание странных ошибок перед переходом к потомкам узла $i$ неплохо бы выяснить количество этих потомков. Ведь для листьев дерева, что не удивительно, формула дает неадекватный результат. Чтобы найти следующего за первым потомка, нужно к его индексу прибавить 1. Это логично, потому что потомки одного узла всегда находятся рядом, без промежутков. Но при итерации по ним нужно вовремя остановиться — определить, какой потомок считается последним.


Поиск последнего потомка узла $i$ проходит в два этапа: определение индекса последней единицы в коде узла — именно она обозначает данного потомка; а затем определение индекса самого потомка:


$lastChildPos(i) = select_0(i+2)-1$


Получив индекс последней единицы в коде узла, необходимо проверить, что бит по этому индексу действительно установлен. Если нет, то вывод напрашивается сам собой: это узел без потомков, лист. Если же бит установлен, то действуем дальше:


$lastChild(i) = rank_1(lastChildPos(i)-1)$


Найдем последнего потомка узла 2 (буква «к»).


$lastChildPos(2) = select_0(2+2)-1=select_0(4)-1=9-1=8$


Бит по индексу 8 равен 1, следовательно, узел 2 — не лист, и мы можем найти индекс его последнего потомка:


$lastChild(i) = rank_1(8-1)=5$


Количество потомков. Простейший способ определить количество потомков — вычесть из индекса последнего потомка узла индекс его первого потомка и прибавить 1:


$childrenCount(i) = lastСhild(i) - firstСhild(i)+1$


Но допустим, у узла $i$ существует соседний узел $i+1$, который располагается на том же уровне дерева, что и $i$. Тогда количество потомков $i$ можно определить как разность индексов первых потомков узлов $i+1$ и $i$:


$childrenCount(i) = firstСhild(i+1) - firstСhild(i)$


Потомки узла также пронумерованы последовательно. Если первый потомок $i$ — это $j$, то второй — $j+1$ и так далее вплоть до потомка соседнего на этом уровне узла $i+1$ (если таковой есть).


Количество потомков листа «и» с индексом 1 ожидаемо нулевое:


$childrenCount(1) =(select_0(2+1) - 2) - (select_0(1+1) - 1) = 3 - 3 = 0$


Поиск родителя для узла $i$ организуется по формуле:


$parent(i) = rank_0(select_1(i+1) - 1) -1$


Воспользуемся ей для поиска родителя узла 6 (буква «к»):


$parent(6) = rank_0(select_1(7) - 1) -1 = rank_0(9) -1 = 3$


Это узел 3, буква «а».


Обладая знанием о формулах для индексов потомка и родителя, не составит труда обойти дерево целиком. Главное — не забывать об обработке граничных условий для корня и листьев.


Пара копеек про методы BP и DFUDS. У обоих методов пространственная асимптотика — $2N + o(N)$ бит для дерева из $N$ узлов, и оба они схожи представлением узла дерева в виде открывающих и закрывающих скобок.


BP (balanced parentheses) конвертирует дерево в последовательность скобок, по паре на каждый узел. Для этого дерево обходится в глубину; каждый узел посещается дважды. При первом посещении записывается открывающая скобка, при повторном — закрывающая. Между ними оказываются скобки дочерних элементов.


Последовательность скобок удобно представить в виде битовой карты, где 1 — открывающая скобка, а 0 — закрывающая. На быстрый поиск в ней заточены все формулы для работы с BP. В отличие от LOUDS, BP позволяет быстро подсчитать размер поддерева и определить ближайшего общего предка у двух узлов. А вот найти $i$-ого потомка гораздо сложнее, чем в LOUDS.


DFUDS (depth-first unary degree sequence) схож одновременно и с BP, и с LOUDS. С BP его объединяет обход дерева в глубину и его скобочное представление. А принцип расстановки скобок такой же, как принцип кодирования узлов в LOUDS. Перед обходом дерева заранее добавляем в скобочную последовательность одну открывающую скобку. Потом при обходе узлов записываем открывающие скобки по количеству потомков, плюс одну закрывающую. Получается, что локальность хранения потомков у DFUDS выше, чем у BP. Вычисление размера поддерева и поиск ближайшего общего предка осуществляются за $O(1)$. Зато определение высоты поддерева и поиск родителя на $j$-ом уровне — тяжелые для DFUDS операции.


Для наглядности сравним методы LOUDS, BP и DFUDS на примере мини-дерева.



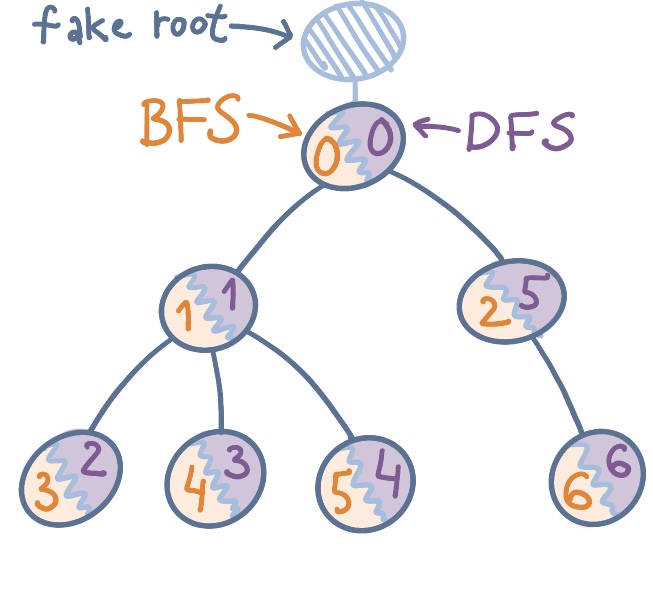
Оранжевым цветом пронумерованы узлы дерева как при обходе в ширину (для LOUDS), синим — как при обходе в глубину (для BP и DFUDS).



LOUDS, BP и DFUDS представления дерева.


Не удивляйтесь, если в англоязычных работах увидите отличия в формулах. Среди математиков встречаются любители индексировать начиная с единицы. А некоторые разработчики считают слова rank и range созвучными, поэтому делают rank на полуинтервале $[0; i)$. Из-за необходимости сохранения симметричности rank/select они вычисляют $select(i)$ как $select(i+1)$. Зато некоторые формулы в таком виде выглядят короче.


Разреженный массив: взболтать, но не смешивать


Разреженный массив (sparse array) — еще одна структура, буквально созданная для сжатия. Размер такого массива порой на порядки превышает количество заполненных элементов. А пустые элементы либо принимают значение по умолчанию, либо помечаются чем-то вроде null. Разреженный массив маячит на горизонте всякий раз при необходимости хранить множество объектов и связей между ними. На ум сразу приходят графы друзей в социальных сетях, алгоритмы ранжирования поисковой выдачи, Excel-подобные таблицы, симуляторы электрических схем с миллиардами транзисторов в чипе.


Зачастую такие массивы по-лавкрафтовски циклопические, при наивной реализации не умещаются в оперативку, оставаясь фактически не заполненными. В зависимости от требований к памяти и скорости разреженные массивы превращают в куда более компактные хэш-таблицы, списки смежности, бинарные деревья… или подвергают succinct'изации.


Допустим, у нас есть разреженный массив строк. Прицепим к нему компактный индексируемый словарь. Что это даст?



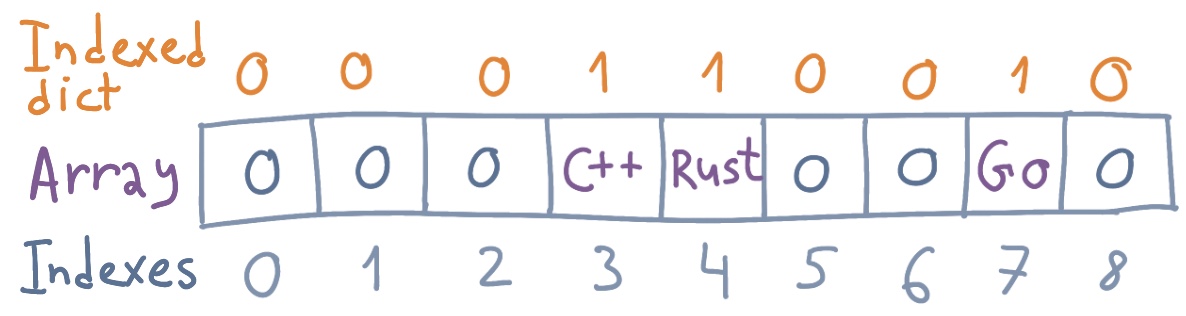
Разреженный массив с битовой картой.


Теперь, не обращаясь к оригинальному массиву напрямую, легко проверить, присутствует ли в нем элемент по интересующему индексу. Ничто не мешает ужать исходный массив, выкинув все не заполненные элементы:



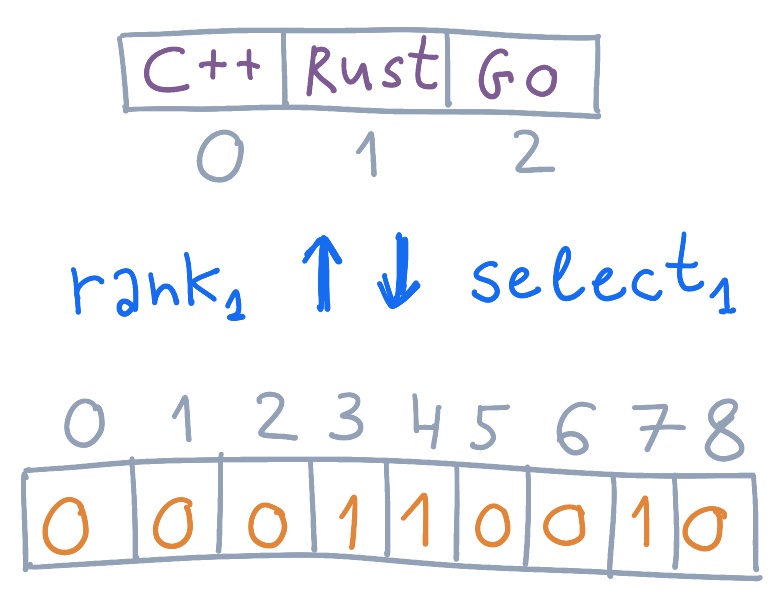
Массив без пустых элементов.


Вычисление индекса в сжатом массиве. После проверки присутствия элемента неплохо бы получить доступ к его значению в исходном массиве, то есть сопоставить индекс $i$ в индексируемом словаре индексу $j$ в сжатом массиве. Не сюрприз, что для этого используется rank:


$j = rank_1(i) -1$


Проверим, как обстоят дела с 8-м элементом: $bitmap[8] = 0$. Значит, в исходном массиве такого элемента нет. А что с элементом 7? $bitmap[7] = 1$. Получим его значение: $rank_1(7) - 1 = 3-1 = 2$. По индексу 2 находится «go».


Вычисление индекса в исходном массиве. Наверняка в массиве потребуется искать элементы по значению! Если данные не сортированы, поиск сводится к перебору за $O(N)$, где $N$ — количество не пустых элементов. Для найденного элемента $j$ может потребоваться получить его индекс $i$, как если бы массив не был ужат. Для этого воспользуемся select — обратной операцией к rank:


$i = select_1(j+1)$


Для примера отыщем строку «C++». В компактном массиве она находится по индексу 0. А ее индекс в исходном массиве равен $select_1(0+1) = 3$.


Уже на примере со строками заметна экономия памяти. Если массив предназначен для хранения классов со множеством полей, экономия становится куда весомее. Кроме того, поиск в компактном массиве работает быстрее, чем в большом и разреженном: он лучше кэшируется процессором. У битового индексируемого словаря больше шансов уместиться в кэш-линию, чем у обычного массива чисел, строк или навороченных пользовательских типов.


Конечно, для хранения $2^{30}$ элементов описанный способ не годится. Его применимость заканчивается там, где начинаются проблемы с разрастанием индекса. Но своя ниша у этого способа сжатия массивов и его вариаций, конечно, есть. Будничный пример — это реализация протокола BitTorrent. Битовая карта содержит информацию о скачанных сегментах файлов, и пиры обмениваются индексами имеющихся у них сегментов. Космический пример — варианты сегментированной передачи данных, которые используют марсоходы, Вояджеры и станция «Новые Горизонты», бороздящая транснептуновые просторы.


Описанные примеры succinct'изации префиксного дерева и разреженного массива построены на общем фундаменте. Он основан на несокрушимой вере в эффективность операций rank/select. Без нее вся теория компактных, но достаточно быстрых структур трещит по швам. От скорости rank и select зависит адекватность использования компактных структур за пределами диссертаций.


Эти операции в самом деле можно реализовать крайне эффективно: rank — за $O(1)$; select — за $O(lg (lg N))$, что тоже почти константа. И конечно без некоторых уловок не обойдется. А так как в любом произведении с запутанным сюжетом должна витать легкая недосказанность, на этом я и остановлюсь.


Интересные факты


Что такое теоретическая нижняя граница занимаемых ресурсов с точки зрения теории информации? Допустим, структура данных хранит множество из $N$ элементов. Чтобы идентифицировать их без коллизий, потребуется количество бит, не меньшее $X=log_2N$. $X$ и есть та самая нижняя граница, определенная по формуле Хартли. В некоторых частных случаях, обладая информацией о природе хранимых данных, структуру удается ужать еще эффективнее.


Считается ли сишная строка succinct структурой данных? Она содержит $N$ символов и завершается нулевым символом ASCII. Значит, занимает $N+1$ места, и поэтому… она succinct, а конкретнее, implicit! Что приводит нас к следующему вопросу.


Все ли succinct структуры одинаково компактны? Область исследования succinct определяет аж три вида компактных структур, различающихся пространственной сложностью:


  • compact — $O(N)$. Линейная сложность от $N$ — количества хранимых элементов. Самые «халявные» в плане требований к сжатию структуры. Так сказать разминка перед настоящим хардкором. Если уж мы заговорили про строки, то подходит следующий пример: последовательность строк переменной длины. Строки хранятся одна за другой, безо всяких разделителей. Для поиска отдельных строк формируется битовая карта, в которой все биты сброшены в 0 кроме битов с индексами, соответствующими началам строк. Эта структура занимает $O(2N)$ (множитель 2 при использовании символов Ландау правильнее всего опустить, но так нагляднее) и позволяет реализовать быстрый select для определения начала каждой строки в последовательности.
  • succinct — $N + o(N)$. Структуры с этой пространственной сложностью — то, что имеется ввиду под succinct data structures по умолчанию. Пример из мира строк: строки наподобие паскалевских (Pascal string), в которых последовательность символов предваряется их количеством. Они занимают $N + log(N)$.
  • implicit — $N + O(1)$. Структуры, дополнительно использующие фиксированное количество памяти. Примеры: куча (heap) и сишная строка. Обе структуры занимают $N + 1$.

Какие еще компактные структуры используются на практике? В смысле, не для научных публикаций по плану кафедры, а в качестве обкатанных боевых решений. В статье речь шла про succinct-префиксные деревья и разреженные массивы. Но это вершина айсберга, в глубине которого кроются компактные вейвлет-деревья, FM-индексы, RMQ (range minimum queries), LCP (longest common prefix), суффиксные массивы и огромное количество других структур, пригодных к succinct'изации. У каждой из них своя сфера использования и свои соотношения эффективности-компактности.


Эпилог


Компактные структуры данных здорово облегчают жизнь разработчикам поисковых движков, мобильных приложений, высоконагруженных сервисов. И не только. В принципе для любого проекта, работающего с растущими объемами данных, может наступить час X, когда бутылочным горлышком внезапно станут структуры данных в их текущей реализации.


Но succinct — не безвредный подорожник на коленку, от которого «хуже-то уж точно не будет». Succinct — это демон со множеством имен. Призвать и управлять им подвластно лишь искушенному демонологу, имеющему кристальное представление о хитростях, опасностях и могуществе succinct. Достоверно известно, что такие храбрецы живут среди нас. Они приложили руку к редактору метода ввода (IME) в Google, компактному представлению ДНК в Гонконгском университете. В MAPS.ME мы используем succinct-реализацию для обработки географических высот.


Как бы то ни было, знание о компактных представлениях для знакомых структур данных однажды может стать судьбоносным при принятии решений об оптимизации проекта. Ибо как сказал Дональд К., в 97 % случаев лучше забыть о микро-оптимизациях: преждевременная оптимизация корень всех зол. Однако мы не должны упускать наши возможности в оставшихся 3 %.


Что дальше?


Для тех, кто жаждет теоретических подробностей из мира succinct:



Для тех, кто желает поскорее перейти от теории к практике: