В последнее время задача распознавания символов в прикладных программах не представляет особой сложности — можно использовать множество готовых OCR-библиотек, многие из которых доведены почти до совершенства. Но все же иногда может возникнуть задача разработать свой алгоритм распознавания без использования сторонних «навороченных» OCR-библиотек.

Именно такая задача возникла у меня по ходу работы, а причин, почему лучше не использовать готовые библиотеки, несколько: закрытость проекта, с его дальнейшей сертификацией, определенное ограничение на количество строчек кода и размер подключаемых библиотек, тем более что по предметной области распознавать приходится достаточно определенный набор символов.

Алгоритм распознавания простой, и, конечно же, не претендует на звание самого точного, быстрого и эффективного, но со своей маленькой задачей справляется хорошо.

Допустим, у нас есть входные данные в виде отсканированных изображений документов, структурированной формы. У этих документов есть специальный односимвольный код расположенный в верхнем левом углу. Наша задача этот символ распознать и дальше произвести какие-нибудь действия, например классифицировать исходный документ по заданным правилам.

Схема алгоритма выглядит следующим образом:

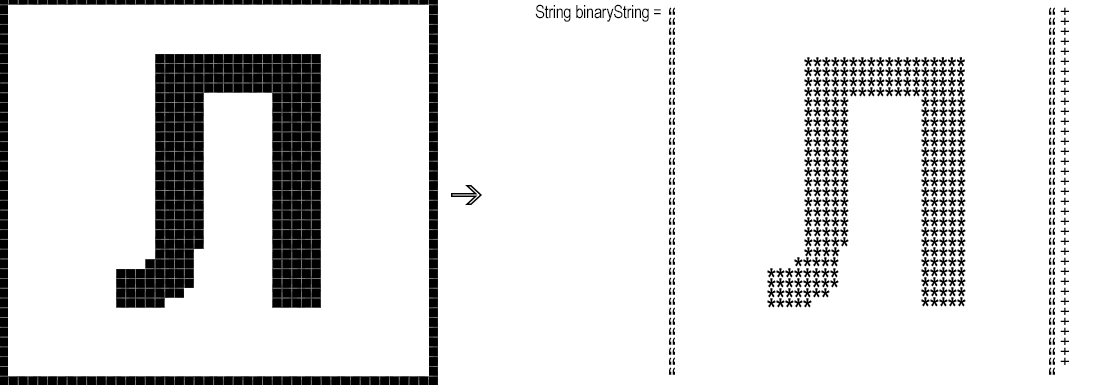
Так как мы заранее знаем где у нас находится символ, вырезать определенную область не составит труда. Для того чтобы убрать все «неровности» краев символа переводим изображение в монохромное (черно-белое).

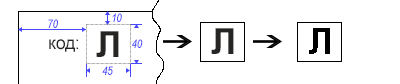
short width = 45, height = 40, offsetTop = -10, offsetLeft = -70;
BufferedImage image = ImageIO.read(file);
BufferedImage symbol = new BufferedImage(width, height, BufferedImage.TYPE_BYTE_BINARY);
Graphics2D g = symbol.createGraphics();
g.drawImage(image, offsetLeft, offsetTop, null);

Далее необходимо преобразовать «попиксельно» полученный фрагмент в бинарную строку, то есть строку, где черному пикселю соответствует, например, '*', а белому — пробел.

short whiteBg = -1;
StringBuilder binaryString = new StringBuilder();  
for (short y = 1; y < height; y++)
   for (short x = 1; x < width; x++) {
       int rgb = symbol.getRGB(x, y);
       binaryString.append(rgb == whiteBg ? " " : "*");
   }

Далее необходимо найти минимальное расстояние Левенштейна между полученной строкой и заранее подготовленными эталонными строками (на самом деле метод сравнения строк можно взять любой).

int min = 1000000;
char findSymbol = "";
for (Map.Entry<Character, String> entry : originalMap.entrySet()) {
     int levenshtein = levenshtein(binaryString.toString(), entry.getValue());
     if (levenshtein < min) {
             min = levenshtein;
             findSymbol = entry.getKey();
     }
}

Функция нахождения расстояния Левенштейна реализована в виде метода по стандартному алгоритму:

public static int levenshtein(String targetStr, String sourceStr) {
        int m = targetStr.length(), n = sourceStr.length();
        int[][] delta = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++)
            delta[i][0] = i;
        for (int j = 1; j <= n; j++)
            delta[0][j] = j;
        for (int j = 1; j <= n; j++)
            for (int i = 1; i <= m; i++) {
                if (targetStr.charAt(i - 1) == sourceStr.charAt(j - 1))
                    delta[i][j] = delta[i - 1][j - 1];
                else
                    delta[i][j] = Math.min(delta[i - 1][j] + 1,
                            Math.min(delta[i][j - 1] + 1, delta[i - 1][j - 1] + 1));
            }
        return delta[m][n];
    }

Полученный findSymbol и будет нашим распознанным символом.

Данный алгоритм можно оптимизировать для повышения быстродействия и дополнить разными проверками для улучшения эффективности распознавания. Многие показатели зависят от конкретной предметной области решаемой задачи (количество символов, разнообразия шрифтов, качества изображения и др.)

Практическим способом было обнаружено, что метод качественно справляется даже с такими проблемными вопросами, как «схожесть» символов, например «Л»<->«П», «5»<->«S», «O»<->«0». Так как, к примеру, расстояние между бинарными строками «Л» и «П» будет всегда больше, чем между распознаваемой «Л» и эталонной строкой «Л», даже с некоторыми «неровностями».

В общем, если Вам необходимо решить похожую задачу (например, распознавание игральных карт), с рядом ограничений по использованию нейронок и других готовых решений, можете смело брать и дорабатывать данный метод.