В циклосферной теории строения электронных оболочек атомов и молекул, предложенной Кеннетом Снельсоном, электроны считаются отрицательно заряженными кольцевыми магнитами. При противоположной ориентации магнитных полей у смежных электронов их края притягиваются друг к другу и формируют электронные оболочки. Наиболее устойчивые оболочки атомов получаются из 8, 10 и 14 электронов.

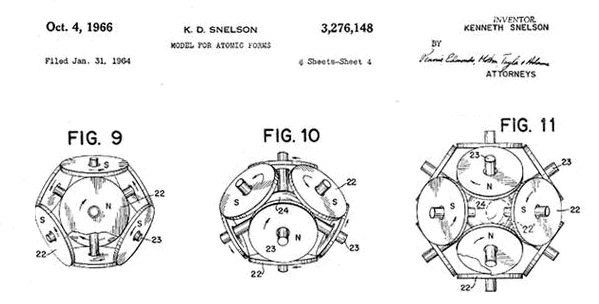
Рис. 1. Иллюстрации к описанию атомных электронных оболочек из патента К. Снельсона

Эта теория хорошо объясняет известные химические свойства и структурные особенности различных простейших молекул, а также длину периодов в таблице Менделеева (см. «Химия Кеннета Снельсона»). И объясняет явно лучше квантовой механики с её многочисленными постулатами — орбиталями, принципом неопределённости, волновыми функциями и т.п.. Зато квантовая механика неплохо справляется с описанием спектральных свойств атома водорода, которые сложно объяснить исходя из простой кольцевой формы электрона. Но можно предположить, что у электрона кольцо не простое, а составное – состоящее из замкнутой цепочки мелких колечек. И попытаться обосновать этим линейчатость спектра водородного атома.

Предположим, что электрон атома водорода в наивысшем возбуждённом состоянии имеет простую кольцевую форму — ту же, что и свободный электрон. А переходы на нижележащие энергетические уровни (стационарные состояния) сопровождаются не только излучением, но и увеличением количества образующих его уменьшенных колечек. Точнее – пар колечек, поскольку только при чётном количестве они удерживаются вместе магнитным полем (Рис. 2).

Рис. 2. Схема основных стационарных состояний электрона

Такая плоская схема демонстрирует только общий принцип дробления электронного кольца. Но в атоме водорода все колечки, образующие электронную цепь, должны располагаться на эквипотенциальной сфере, для показа которой лучше использовать объёмные изображения (Рис. 3).

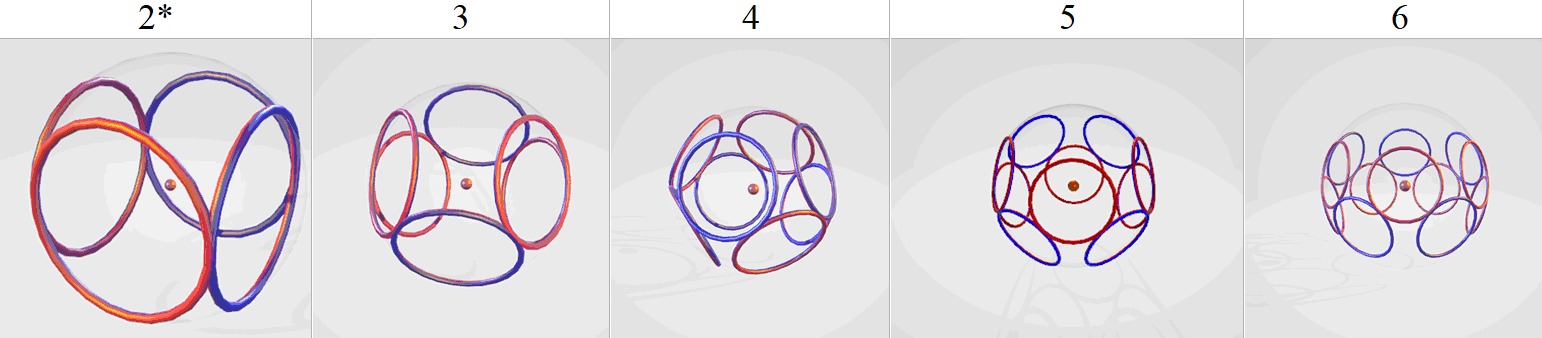
* Цифры соответствуют количеству пар электронных колец

Рис. 3. Низшие многокольцевые состояния электрона

Существование пяти основных спектральных серий атомарного водорода – Лаймана, Бальмера, Пашена, Брэккета и Пфунда – может объясняться излучательными переходами электрона на энергетические уровни, соответствующие этой пятёрке стационарных состояний (2, 3, 4, 5 и 6 пар колец). В таком случае существование серии Хэмпфри объясняется переходом электрона из однокольцевого состояния в двухкольцевое (или в соответствующее ему двухволновое). А многочисленность спектральных линий у этой серии может отражать множество возможных колебательных состояний однокольцевого электрона (Рис. 4).

* Цифры соответствуют количеству стоячих волн в электронном кольце

Рис. 4. Низшие колебательные состояния электрона

На схеме основных стационарных состояний электрона (Рис. 2) показана его гипотетическая двухкольцевая форма. Логично предположить, что она может формироваться из однокольцевого двухволнового варианта. Но ещё логичнее выглядит трансформация двухволнового кольца в четырёхкольцевую форму. Во всяком случае, при построении 3D-моделей трансформация четырёх колец в две волны (и наоборот) не вызывает затруднений (Рис. 5).

Рис. 5. Переходные формы электрона (двухволновой <--> четырёхкольцевой)

Если переходная двухкольцевая форма всё-таки существует, то её энергетический уровень не должен отличаться от уровня двухволновой формы. Поэтому её совсем не обязательно показывать на схеме излучательных переходов электрона в атоме водорода (Рис. 6).

Рис. 6. Серии излучательных переходов электрона в атоме водорода

Известны и другие серии излучения электрона, но все они лежат в далёкой инфракрасной области и с трудом поддаются изучению. Последняя, получившая именное название, — серия Хансена-Стронга – была описана в 1972 году. На приведённой выше схеме её основному энергетическому уровню соответствует трёхволновое состояние электрона.

У свободного кольцевого электрона, на который не действует поле притяжения атомного ядра, невозбуждённое состояние в идеале должно соответствовать наивысшему (нулевому) энергетическому уровню, показанному на Рис. 6. Такой идеал возможен только при бесконечно большом количестве стоячих волн, энергия которых стремится к нулевому пределу. Но достичь этого предела невозможно. Поэтому свободный кольцевой электрон всегда близок к идеалу (нулевому энергетическому состоянию), но не идеален. Причём его энергия при снижении количества (и увеличении амплитуды) стоячих волн не уменьшается, как в атоме водорода, а увеличивается.

Существование множества колебательных состояний свободного кольцевого электрона не представляет особого интереса для химиков, но способно пролить свет на некоторые астрофизические явления. Например, объяснить причины существования реликтового микроволнового излучения, обосновать концепцию старения света, дать альтернативное объяснение красному смещению, опровергнуть теорию Большого взрыва и доказать вечность и бесконечность Вселенной. Но сначала нужно доработать теорию Кеннета Снельсона – доказать, что электронные оболочки атомов и молекул можно строить не только из простых колец, но и из их многокольцевых цепочек.

Иллюстрации к этой заметке подготовлены 3DKiwi, за что автор выражает ему свою глубочайшую благодарность. Им же построены наглядные 3D-модели основных стационарных состояний электрона атома водорода, позволяющие детально рассмотреть все подробности:
https://p3d.in/2d5ol — 6 пар колец
https://p3d.in/DtkLu — 5 пар
https://p3d.in/TrAmL — 4 пары
https://p3d.in/fhaVp — 3 пары
https://p3d.in/9uWEb — 2 пары
https://p3d.in/gAwto — 2 волны
https://p3d.in/Te4xo — 3 волны
https://p3d.in/DkhLr — 4 волны
https://p3d.in/ZChp6 — 5 волн
https://p3d.in/o3S47 — 6 волн
https://p3d.in/CkBMl — 7 волн

Наверное, Снельсон одобрил бы эти модели. Если бы не умер в конце 2016 года.