Поиск и маркировка связных компонентов в бинарных изображениях — один из базовых алгоритмов анализа и обработки изображений. В частности, этот алгоритм может быть использован в машинной зрении для поиска и подсчета единых структур в изображении, с последующих их анализом.
В рамках этой статьи будут рассмотрены два алгоритма для маркировки связных компонентов, показана их реализация на языке программирования F#. А также, произведен сравнительный анализ алгоритмов, поиск слабых мест. Исходный материал для реализации алгоритмов был взят из книги “Компьютерное зрение” (авторы Л. Шапиро, Дж. Стокман. перевод с английского А. А. Богуславского под редакцией С. М. Соколова).
Звучит заумно, поэтому давайте просто посмотрим картинку. Примем за основу, что пиксели переднего плана бинарного изображения помечены как 1, а фоновые пиксели помечены 0.
После обработки изображения алгоритмом маркировки связных компонентов мы получим следующую картину. Здесь, вместо пикселей сформированы связные компоненты, отличающиеся друг от друга цифрой. В этом примере таких компонент найдено 5 штук и с ними можно будет работать, как с отдельными сущностями.
Figure 1: Маркированные связные компоненты
Ниже будут рассмотрены два алгоритма, которые могут быть использованы для решения такой задачи.
Мы начнем с рассмотрения алгоритма, построенного на рекурсии, как наиболее очевидного. Принцип работы такого алгоритма будет следующим
Назначаем метку, которой будем помечать связанные компоненты, начальным значением.
Таким образом, перебирая все точки массива и вызывая для каждой рекурсивный алгоритм, то в конце перебора мы получим полностью промаркированную таблицу. Так как присутствует проверка на то, была ли уже данная точка промаркирована, каждая точка будет обработана только один раз. Глубина рекурсии будет зависеть только от количества связанных соседей к текущей точке. Данный алгоритм хорошо подходит для изображений, в которых нет большой заливки изображений. То есть изображения, на которых присутствуют тонкие и короткие линии, а все остальное является фоновым изображением, которое не обрабатывается. При этом скорость такого алгоритма может быть выше построчного алгоритма (о нем речь будет ниже по статье).
Так как двумерные бинарные изображения являются двумерными матрицами, то при написании алгоритма я буду оперировать понятиями матриц, о которых делал отдельную статью, которую можно почитать здесь
Функциональное программирование на примере работы с матрицами из теории линейной алгебры
Рассмотрим и подробно разберем F#-функцию, которая реализует рекурсивный алгоритм маркировки связных компонентов бинарного изображения
Объявляем функцию recMarkingOfConnectedComponents, принимающую двумерный массив matrix, упакованный в запись типа Matrix. Функция не будет менять исходный массив, поэтому сначала создаем его копию, которая будет обрабатываться алгоритмом и возвращаться.
Для упрощения проверок индексов запрашиваемых точек за пределы массива создадим активный шаблон, который возвращает одно из трех значений.
Out — запрашиваемый индекс вышел за пределы двумерного массива
Zero — точка содержит фоновый пиксель (равна нулю)
Value — запрашиваемый индекс находится в пределах массива
Данный шаблон упростит проверку координаты точки изображения при очередном кадре рекурсии:
Функция MarkBits объявлена как рекурсивная и служит для обработки текущего пикселя и всех его соседей (верхнего, нижнего, левого, правого):
Функция принимает на вход следующие параметры:
x — номер строки
y — номер столбца
value — текущее значение метки, которым нужно пометить пиксель
При помощи конструкции match/with и активного шаблона (приведенного выше) делается проверка координат пикселя, чтобы он не вышел за пределы двумерного массива. Если точка находится внутри двумерного массива, то делаем предварительную проверку, чтобы не обрабатывать точку, которая уже была обработана.
В противном случае возникнет бесконечная рекурсия и алгоритм не будет работать.
Далее, маркируем точку текущим значением маркера:
И обрабатываем всех его соседей, рекурсивно вызывая эту же функцию:
После того, как алгоритм мы реализовали, его нужно использовать. Рассмотрим код подробнее.
Перед обработкой изображения установим начальное значение метки, которой будем помечать связные группы пикселей.
Дело в том, что фронтовые пиксели в бинарном изображении уже установлены в 1, поэтому, если начальное значение метки будет тоже равно 1, то алгоритм работать не будет. Поэтому начальное значение метки должно быть больше чем 1. Есть и другой способ решения проблемы. Перед запуском алгоритма отметить все пиксели, установленные в 1, начальным значением -1. Тогда мы сможем установить value в 1. Вы это сможете сделать самостоятельно, если захотите
Следующая конструкция при помощи функции Array2D.iteri перебирает все точки массива, и если во время перебора встречается точка, установленная в 1, то это значит, что она является не обработанной и для нее нужно вызвать рекурсивную функцию markBits с текущим значением метки. Все пиксели, установленные в 0, алгоритм игнорирует.
После рекурсивной обработки точки можно считать, что вся связная группа, к которой эта точка относится, гарантированно промаркирована и можно увеличить значение метки на 1, чтобы применить его к следующей связной точки.
Рассмотрим пример применения такого алгоритма.
К достоинствам рекурсивного алгоритма относится его простота в написании и понимании. Он отлично подходит для бинарных изображений, содержащее большой фон и с вкраплениями небольших групп пикселей (например, линии, не крупные пятна и так далее). В таком случае скорость обработки изображение может быть высокой, так как алгоритм обрабатывает все изображение за один проход.
Недостатки также очевидны — это рекурсия. Если изображение состоит из крупных пятен или вообще целиком залито, тогда скорость обработки резко снижается (на порядки) и возникает риск того, что программа вообще аварийно закончит свою работу из-за нехватки свободного места в стеке.
К сожалению в данном алгоритме нельзя применить принцип хвостовой рекурсии, потому что хвостовая рекурсия предъявляет два требования:
В нашем случае рекурсия не выполняет никаких конечных вычислений, который можно передать следующему кадру рекурсии, а просто модифицирует двумерный массив. В принципе, это можно было бы обойти, просто возвращая некоторое холостое число, которое само по себе ничего не значит. Также мы рекурсивно делаем 4 вызова, так как нам нужно обработать всех четырех соседей точки.
У алгоритма есть и другое название “Алгоритм построчной маркировки” и здесь мы попытаемся его разобрать.
Определение выше еще больше запутывает, поэтому мы попробуем разобраться с принципом работы алгоритма по другому и начнем издалека.
Сначала разберемся с определением четырехсвязной и восьмисвязной окрестностями текущей точки. Посмотрите на картинках ниже, чтобы понять что это такое и в чем отличие.
Figure 2: Четырехсвязная компонента
\begin{matrix}
& 1 & \\
2 & * & 3 \\
& 4 &
\end{matrix}
Figure 2: Восьмисвязная компонента
\begin{matrix}
1 & 2 & 3 \\
4 & * & 5 \\
6 & 7 & 8
\end{matrix}
Первая картинка показывает четырехсвязную компоненту точки, то есть это значит, алгоритм обрабатывает 4-ех соседей текущей точки (слева, справа, сверху и снизу). Соответственно, восьмисвязная компонента точки означает, что у нее есть 8 соседей. В рамках данной статьи мы будет работать с четырехсвязными компонентами.
Теперь нужно разобраться, что такое структура данных для объединения поиска, построенная на некоторых множествах?
Для примера допустим, что у нас есть два множества
Эти множества организованы в виде следующих деревьев:
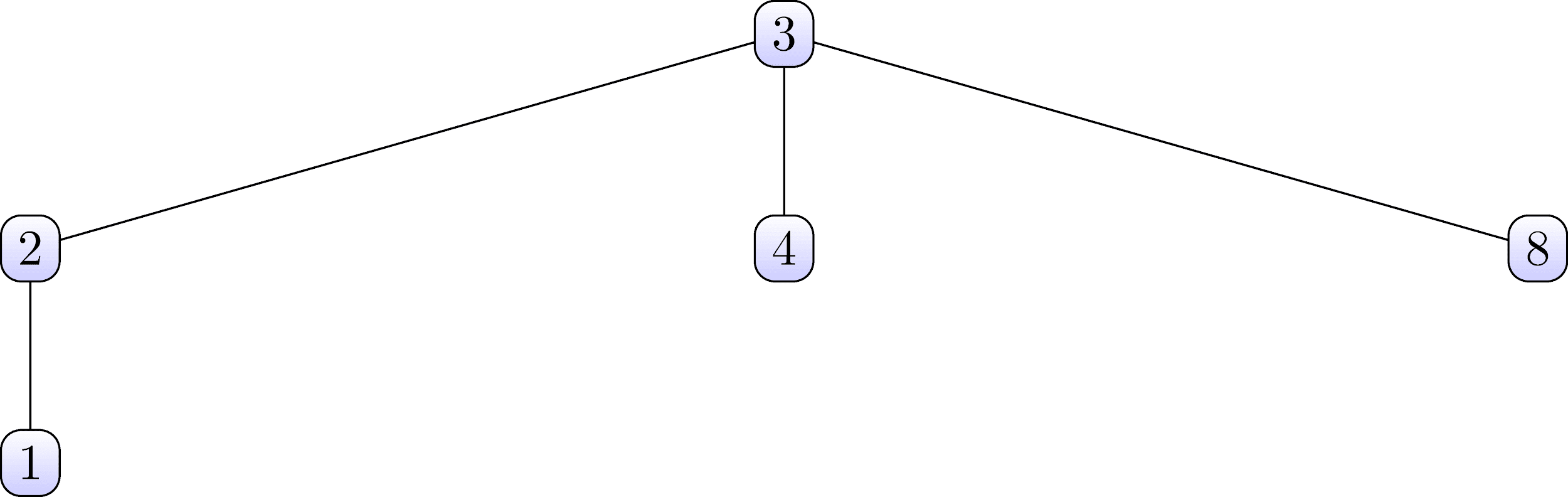

Обратите внимание, что в первом множестве нод 3 является корневым, а во втором — нод 6.
Теперь рассмотрим структуру данных для объединения-поиска, которое содержит в себе оба этих множества, а также организует их древовидную структуру.
Figure 4: Структура данных для объединения-поиска
\begin{matrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
2 & 3 & 0 & 3 & 7 & 7 & 0 & 3
\end{matrix}
Посмотрите внимательно на таблицу выше и попробуйте найти связь с деревьями множеств, которые показаны выше. Рассматривать таблицу следует по вертикальным столбцам. Видно, что числу 3 в первой строке соответствует число 0 во второй строке. И в первом дереве число 3 является корнем первого множества. По аналогии можно найти, что числу 7 из первой строки соответствует число 0 из второй строки. Число 7 также является корнем дерева второго множества.
Таким образом приходим к выводу, что числа из верхнего ряда представляют собой дочерние ноды множеств, а соответствующие числа из нижнего ряда — их родительские ноды. Руководствуясь этим правилом вы легко можете восстановить оба дерева из приведенной таблицы.
Мы разбираем такие детали для того, чтобы впоследствии нам было проще разобраться в том, как работает алгоритм построчной маркировки. Пока что остановимся на том, что ряд чисел из первого ряда — это всегда числа от 1 до некоторого максимального числа. По сути максимальное число первого ряда представляет из себя максимальное значение меток, которыми будут маркироваться найденные связные компоненты. А отдельные множества — переходы между метками, которые образуются в результате первого прохода (подробнее рассмотрим позже).
Перед тем, как продолжить, рассмотрим псевдокод некоторых функций, которые будут использоваться алгоритмом.
Обозначим таблицу, представляющую собой структуру данных для объединения-поиска, как PARENT. Следующая функция называется find и будет принимать в качестве параметров текущую метку X и массив PARENT. Эта процедура прослеживает родительские указатели вверх к корню дерева и находит метку корневого узла дерева, которому принадлежит X.
Рассмотрим, как такую функцию можно реализовать на F#
Здесь мы объявляем рекурсивную функцию find, которая принимает текущую метку X. Массив PARRENT здесь не передается, так как он у нас уже есть в глобальном пространстве имен и функция его уже видит и может с ним работать.
Сначала функция пытается найти индекс метки в верхней строке (так как нужно найти его родителя, который расположен в нижней строке.
Если поиск увенчался успешно, то мы получаем его родителя и сравниваем с 0. Если родитель не равен 0, значит у этого нода тоже есть родитель и функция рекурсивно вызывает саму себя до тех пор, пока родитель не будет равен 0. Это будет означать, что мы нашли корневой нод множества.
Следующая функция, которая нам понадобится, называется union. Она принимает две метки X и Y, а также массив PARENT. Эта структура модифицирует (если необходимо) PARENT для слияния подмножества, содержащего метку X, с множеством, содержащим метку Y. Процедура ищет корневые узлы обеих меток и если они не совпадают, то узел одной из метки назначается родительским узлом второй метки. Так происходит объединение двух множеств.
Реализация на F# выглядит так
Обратите внимание, что здесь уже используется функция find, которую мы уже реализовали.
Также алгоритм требует дополнительных двух функций, которые называются neighbors и labels. Функция neighbors возвращает множество соседних точек слева и сверху (так как в нашем случае алгоритм работает по четырехсвязной компоненте) от заданного пикселя, а функция labels — возвращает множество меток, которые уже были присвоены заданному множеству пикселей, которые вернула функция neighbors. В нашем случае мы не будем реализовывать две эти функции, а сделаем только одну, которая объединит в себе обе функции и вернет найденные метки.
Забегая вперед сразу скажу, что массив step1, который использует функция уже существует в глобальном пространстве и содержит в себе результат обработки алгоритма при первом проходе. Хочу обратить особое внимание на дополнительный фильтр.
Он отсекает все результаты, которые равны 0. То есть, если метка содержит в себе 0, то мы имеем дело с точкой фонового изображения, которую обрабатывать не нужно. Это очень важный нюанс, который не упомянут в книге, из которой мы берем примеры, но тем не менее без такой проверки алгоритм работать не будет.
Постепенно, шаг за шагом мы приближаемся с самой сути алгоритма. Давайте еще раз посмотрим на изображение, которое нам нужно будет обработать.
Figure 5: Исходное бинарное изображение
\begin{matrix}
1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 \\
1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 \\
0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 \\
1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\
1 & 1 & 0 & 1 & 0 & 1 & 1 & 1
\end{matrix}
Перед обработкой создадим пустой массив step1, в котором будет сохраняться результат первого прохода.
Figure 6: Массив step1 для хранение результатов первичной обработки
\begin{matrix}
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Рассмотрим первые несколько шагов первичной обработки данных (только первые три строчки исходного бинарного изображения).
Перед тем, как пошагово рассмотреть алгоритм, посмотрим на псевдокод, которые объясняет общий принцип работы.
Figure 7: Шаг 1. Точка (0,0), label = 1
\begin{matrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Figure 8: Шаг 2. Точка (1,0), label = 1
\begin{matrix}
1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Figure 9: Шаг 2. Точка (2,0), label = 1
\begin{matrix}
1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Figure 10: Шаг 4. Точка (3,0), label = 2
\begin{matrix}
1 & 1 & 0 & 2 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Figure 11: Шаг последний, окончательный результат первого прохода
\begin{matrix}
1 & 1 & 0 & 2 & 2 & 2 & 0 & 3 \\
1 & 1 & 0 & 2 & 0 & 2 & 0 & 3 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\
4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\
0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\
6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\
6 & 6 & 0 & 4 & 0 & 7 & 7 & 3
\end{matrix}
Обратите внимание, что в результате первичной обработки исходного изображения у нас получилось два множества
Визуально это видно как соприкосновение меток 1 и 2 (координата точек (1,3) и (2,3)) и меток 3 и 7 (координата точек (7,7) и (7,6)). С точки зрения структуры данных для объединения-поиска получился такой результат.
Figure 12: Вычисленная структура-данных для объединения поиска
\begin{matrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 \\
0 & 1 & 0 & 0 & 0 & 0 & 3
\end{matrix}
После окончательно обработки изображения с помощью полученной структуры-данных мы получаем следующий результат.
Figure 13: Окончательный результат
\begin{matrix}
1 & 1 & 0 & 1 & 1 & 1 & 0 & 3 \\
1 & 1 & 0 & 1 & 0 & 1 & 0 & 3 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\
4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\
0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\
6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\
6 & 6 & 0 & 4 & 0 & 3 & 3 & 3
\end{matrix}
Теперь все связные компоненты у нас имеют уникальные метки и их можно использовать в последующих алгоритма для обработки.
Реализация кода на F# выглядит следующим образом
Построчное объяснение кода уже не имеет смысла, так как все было рассказано выше. Здесь можно просто сопоставить код F# с псевдокодом, чтобы стало понятно, как он работает.
Давайте сравним скорость обработки данных обоими алгоритмами (рекурсивный и построчный).
Как видно, на таком примере скорость работы рекурсивного алгоритма существенно превышает скорость построчного алгоритма. Но все меняется как только мы начинаем обрабатывать картинку, залитую сплошным цветом и для наглядности также увеличим ее размеры до 100х100 пикселей.
Как видим, рекурсивный алгоритм уже в 25 раз работает медленнее линейного. Давайте увеличим размер картинки до 200х200 пикселей.
Разница уже во много сотен раз. Отмечу, что уже при размере 300х300 пикселей рекурсивный алгоритм вызывает переполнение стека и программа аварийно завершает свою работу.
В рамках данной статьи был рассмотрен один из базовых алгоритмов маркировки связных компонентов для обработки бинарных изображений на примере функционального языка F#. Здесь были приведены примеры реализации рекурсивного и классического алгоритмов, объяснен их принцип работы, произведен сравнительный анализ на конкретных примерах.
Исходный код, рассмотренный здесь, также можно посмотреть на гитхабе
MatrixAlgorithms
Надеюсь, статья была интересна тем, кто интересуется F# и алгоритмами по обработке изображений в частности.
В рамках этой статьи будут рассмотрены два алгоритма для маркировки связных компонентов, показана их реализация на языке программирования F#. А также, произведен сравнительный анализ алгоритмов, поиск слабых мест. Исходный материал для реализации алгоритмов был взят из книги “Компьютерное зрение” (авторы Л. Шапиро, Дж. Стокман. перевод с английского А. А. Богуславского под редакцией С. М. Соколова).
Введение
Связная компонента со значением v — это множество C таких пикселов, которые имеют значение v и каждая пара этих пикселов является связной по значению v
Звучит заумно, поэтому давайте просто посмотрим картинку. Примем за основу, что пиксели переднего плана бинарного изображения помечены как 1, а фоновые пиксели помечены 0.
После обработки изображения алгоритмом маркировки связных компонентов мы получим следующую картину. Здесь, вместо пикселей сформированы связные компоненты, отличающиеся друг от друга цифрой. В этом примере таких компонент найдено 5 штук и с ними можно будет работать, как с отдельными сущностями.
Figure 1: Маркированные связные компоненты
Ниже будут рассмотрены два алгоритма, которые могут быть использованы для решения такой задачи.
Рекурсивный алгоритм маркировки
Мы начнем с рассмотрения алгоритма, построенного на рекурсии, как наиболее очевидного. Принцип работы такого алгоритма будет следующим
Назначаем метку, которой будем помечать связанные компоненты, начальным значением.
- Перебираем все точки таблицы, начиная с координаты 0х0 (левый верхний угол). После обработки очередной точки увеличиваем метку на единицу
- Если пиксель по текущей координате равен 1, то сканируем всех четырех соседей этой точки (верхний, нижний, правый, левый)
- Если соседняя точка тоже равна 1, то функция рекурсивно вызывает саму себя для обработки соседа до тех пор, пока не упрется в границу массива или точку 0
- Во время рекурсивной обработки соседа должна быть произведена проверка, что точка не была уже обработана и помечена текущим маркером.
Таким образом, перебирая все точки массива и вызывая для каждой рекурсивный алгоритм, то в конце перебора мы получим полностью промаркированную таблицу. Так как присутствует проверка на то, была ли уже данная точка промаркирована, каждая точка будет обработана только один раз. Глубина рекурсии будет зависеть только от количества связанных соседей к текущей точке. Данный алгоритм хорошо подходит для изображений, в которых нет большой заливки изображений. То есть изображения, на которых присутствуют тонкие и короткие линии, а все остальное является фоновым изображением, которое не обрабатывается. При этом скорость такого алгоритма может быть выше построчного алгоритма (о нем речь будет ниже по статье).
Так как двумерные бинарные изображения являются двумерными матрицами, то при написании алгоритма я буду оперировать понятиями матриц, о которых делал отдельную статью, которую можно почитать здесь
Функциональное программирование на примере работы с матрицами из теории линейной алгебры
Рассмотрим и подробно разберем F#-функцию, которая реализует рекурсивный алгоритм маркировки связных компонентов бинарного изображения
let recMarkingOfConnectedComponents matrix =
let copy = Matrix.clone matrix
let (|Value|Zero|Out|) (x, y) =
if x < 0 || y < 0
|| x > (copy.values.[0, *].Length - 1)
|| y > (copy.values.[*, 0].Length - 1) then
Out
else
let row = copy.values.[y, *]
match row.[x] with
| 0 -> Zero
| v -> Value(v)
let rec markBits x y value =
match (x, y) with
| Value(v) ->
if value > v then
copy.values.[y, x] <- value
markBits (x + 1) y value
markBits (x - 1) y value
markBits x (y + 1) value
markBits x (y - 1) value
| Zero | Out -> ()
let mutable value = 2
copy.values
|> Array2D.iteri (fun y x v -> if v = 1 then
markBits x y value
value <- value + 1)
copy
Объявляем функцию recMarkingOfConnectedComponents, принимающую двумерный массив matrix, упакованный в запись типа Matrix. Функция не будет менять исходный массив, поэтому сначала создаем его копию, которая будет обрабатываться алгоритмом и возвращаться.
let copy = Matrix.clone matrix
Для упрощения проверок индексов запрашиваемых точек за пределы массива создадим активный шаблон, который возвращает одно из трех значений.
Out — запрашиваемый индекс вышел за пределы двумерного массива
Zero — точка содержит фоновый пиксель (равна нулю)
Value — запрашиваемый индекс находится в пределах массива
Данный шаблон упростит проверку координаты точки изображения при очередном кадре рекурсии:
let (|Value|Zero|Out|) (x, y) =
if x < 0 || y < 0
|| x > (copy.values.[0, *].Length - 1)
|| y > (copy.values.[*, 0].Length - 1) then
Out
else
let row = copy.values.[y, *]
match row.[x] with
| 0 -> Zero
| v -> Value(v)
Функция MarkBits объявлена как рекурсивная и служит для обработки текущего пикселя и всех его соседей (верхнего, нижнего, левого, правого):
let rec markBits x y value =
match (x, y) with
| Value(v) ->
if value > v then
copy.values.[y, x] <- value
markBits (x + 1) y value
markBits (x - 1) y value
markBits x (y + 1) value
markBits x (y - 1) value
| Zero | Out -> ()
Функция принимает на вход следующие параметры:
x — номер строки
y — номер столбца
value — текущее значение метки, которым нужно пометить пиксель
При помощи конструкции match/with и активного шаблона (приведенного выше) делается проверка координат пикселя, чтобы он не вышел за пределы двумерного массива. Если точка находится внутри двумерного массива, то делаем предварительную проверку, чтобы не обрабатывать точку, которая уже была обработана.
if value > v thenВ противном случае возникнет бесконечная рекурсия и алгоритм не будет работать.
Далее, маркируем точку текущим значением маркера:
copy.values.[y, x] <- valueИ обрабатываем всех его соседей, рекурсивно вызывая эту же функцию:
markBits (x + 1) y value
markBits (x - 1) y value
markBits x (y + 1) value
markBits x (y - 1) value
После того, как алгоритм мы реализовали, его нужно использовать. Рассмотрим код подробнее.
let mutable value = 2
copy.values
|> Array2D.iteri (fun y x v -> if v = 1 then
markBits x y value
value <- value + 1)
Перед обработкой изображения установим начальное значение метки, которой будем помечать связные группы пикселей.
let mutable value = 2Дело в том, что фронтовые пиксели в бинарном изображении уже установлены в 1, поэтому, если начальное значение метки будет тоже равно 1, то алгоритм работать не будет. Поэтому начальное значение метки должно быть больше чем 1. Есть и другой способ решения проблемы. Перед запуском алгоритма отметить все пиксели, установленные в 1, начальным значением -1. Тогда мы сможем установить value в 1. Вы это сможете сделать самостоятельно, если захотите
Следующая конструкция при помощи функции Array2D.iteri перебирает все точки массива, и если во время перебора встречается точка, установленная в 1, то это значит, что она является не обработанной и для нее нужно вызвать рекурсивную функцию markBits с текущим значением метки. Все пиксели, установленные в 0, алгоритм игнорирует.
После рекурсивной обработки точки можно считать, что вся связная группа, к которой эта точка относится, гарантированно промаркирована и можно увеличить значение метки на 1, чтобы применить его к следующей связной точки.
Рассмотрим пример применения такого алгоритма.
let a = array2D [[1;1;0;1;1;1;0;1]
[1;1;0;1;0;1;0;1]
[1;1;1;1;0;0;0;1]
[0;0;0;0;0;0;0;1]
[1;1;1;1;0;1;0;1]
[0;0;0;1;0;1;0;1]
[1;1;0;1;0;0;0;1]
[1;1;0;1;0;1;1;1]]
let A = Matrix.ofArray2D a
let t = System.Diagnostics.Stopwatch.StartNew()
let R = Algorithms.recMarkingOfConnectedComponents A
t.Stop()
printfn "origin =\n %A" A.values
printfn "rec markers =\n %A" R.values
printfn "elapsed recurcive = %O" t.Elapsed
origin =
[[1; 1; 0; 1; 1; 1; 0; 1]
[1; 1; 0; 1; 0; 1; 0; 1]
[1; 1; 1; 1; 0; 0; 0; 1]
[0; 0; 0; 0; 0; 0; 0; 1]
[1; 1; 1; 1; 0; 1; 0; 1]
[0; 0; 0; 1; 0; 1; 0; 1]
[1; 1; 0; 1; 0; 0; 0; 1]
[1; 1; 0; 1; 0; 1; 1; 1]]
rec markers =
[[2; 2; 0; 2; 2; 2; 0; 3]
[2; 2; 0; 2; 0; 2; 0; 3]
[2; 2; 2; 2; 0; 0; 0; 3]
[0; 0; 0; 0; 0; 0; 0; 3]
[4; 4; 4; 4; 0; 5; 0; 3]
[0; 0; 0; 4; 0; 5; 0; 3]
[6; 6; 0; 4; 0; 0; 0; 3]
[6; 6; 0; 4; 0; 3; 3; 3]]
elapsed recurcive = 00:00:00.0037342
К достоинствам рекурсивного алгоритма относится его простота в написании и понимании. Он отлично подходит для бинарных изображений, содержащее большой фон и с вкраплениями небольших групп пикселей (например, линии, не крупные пятна и так далее). В таком случае скорость обработки изображение может быть высокой, так как алгоритм обрабатывает все изображение за один проход.
Недостатки также очевидны — это рекурсия. Если изображение состоит из крупных пятен или вообще целиком залито, тогда скорость обработки резко снижается (на порядки) и возникает риск того, что программа вообще аварийно закончит свою работу из-за нехватки свободного места в стеке.
К сожалению в данном алгоритме нельзя применить принцип хвостовой рекурсии, потому что хвостовая рекурсия предъявляет два требования:
- каждый кадр рекурсии должен производить вычисления и полученный результат добавлять в аккумулятор, который будет передаваться вниз по стеку.
- В одном кадре рекурсии не должно быть больше одного рекурсивного вызова функции.
В нашем случае рекурсия не выполняет никаких конечных вычислений, который можно передать следующему кадру рекурсии, а просто модифицирует двумерный массив. В принципе, это можно было бы обойти, просто возвращая некоторое холостое число, которое само по себе ничего не значит. Также мы рекурсивно делаем 4 вызова, так как нам нужно обработать всех четырех соседей точки.
Классический алгоритм маркировки связных компонентов на основе структуры данных для объединения поиска
У алгоритма есть и другое название “Алгоритм построчной маркировки” и здесь мы попытаемся его разобрать.
Алгоритм обрабатывает изображение за два прохода. При первом проходе определяются классы эквивалентности и присваиваются врЕменные метки. На втором проходе каждая врЕменная метка заменяется меткой соответствующего класса эквивалентности. Между первым и вторым проходами записанное множество отношений эквивалентности, сохраненное в виде бинарном таблицы, обрабатывается с целью определения классов эквивалентности.
Определение выше еще больше запутывает, поэтому мы попробуем разобраться с принципом работы алгоритма по другому и начнем издалека.
Сначала разберемся с определением четырехсвязной и восьмисвязной окрестностями текущей точки. Посмотрите на картинках ниже, чтобы понять что это такое и в чем отличие.
Figure 2: Четырехсвязная компонента
\begin{matrix}
& 1 & \\
2 & * & 3 \\
& 4 &
\end{matrix}
Figure 2: Восьмисвязная компонента
\begin{matrix}
1 & 2 & 3 \\
4 & * & 5 \\
6 & 7 & 8
\end{matrix}
Первая картинка показывает четырехсвязную компоненту точки, то есть это значит, алгоритм обрабатывает 4-ех соседей текущей точки (слева, справа, сверху и снизу). Соответственно, восьмисвязная компонента точки означает, что у нее есть 8 соседей. В рамках данной статьи мы будет работать с четырехсвязными компонентами.
Теперь нужно разобраться, что такое структура данных для объединения поиска, построенная на некоторых множествах?
Для примера допустим, что у нас есть два множества
Эти множества организованы в виде следующих деревьев:


Обратите внимание, что в первом множестве нод 3 является корневым, а во втором — нод 6.
Теперь рассмотрим структуру данных для объединения-поиска, которое содержит в себе оба этих множества, а также организует их древовидную структуру.
Figure 4: Структура данных для объединения-поиска
\begin{matrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
2 & 3 & 0 & 3 & 7 & 7 & 0 & 3
\end{matrix}
Посмотрите внимательно на таблицу выше и попробуйте найти связь с деревьями множеств, которые показаны выше. Рассматривать таблицу следует по вертикальным столбцам. Видно, что числу 3 в первой строке соответствует число 0 во второй строке. И в первом дереве число 3 является корнем первого множества. По аналогии можно найти, что числу 7 из первой строки соответствует число 0 из второй строки. Число 7 также является корнем дерева второго множества.
Таким образом приходим к выводу, что числа из верхнего ряда представляют собой дочерние ноды множеств, а соответствующие числа из нижнего ряда — их родительские ноды. Руководствуясь этим правилом вы легко можете восстановить оба дерева из приведенной таблицы.
Мы разбираем такие детали для того, чтобы впоследствии нам было проще разобраться в том, как работает алгоритм построчной маркировки. Пока что остановимся на том, что ряд чисел из первого ряда — это всегда числа от 1 до некоторого максимального числа. По сути максимальное число первого ряда представляет из себя максимальное значение меток, которыми будут маркироваться найденные связные компоненты. А отдельные множества — переходы между метками, которые образуются в результате первого прохода (подробнее рассмотрим позже).
Перед тем, как продолжить, рассмотрим псевдокод некоторых функций, которые будут использоваться алгоритмом.
Обозначим таблицу, представляющую собой структуру данных для объединения-поиска, как PARENT. Следующая функция называется find и будет принимать в качестве параметров текущую метку X и массив PARENT. Эта процедура прослеживает родительские указатели вверх к корню дерева и находит метку корневого узла дерева, которому принадлежит X.
Поиск родительскои? метки для заданнои? метки множества.
X — метка множества
PARENT — массив, представляющии? структуру данных для объединения-поиска
procedure find(X, PARENT);
{
j := X;
while PARENT[j] <> 0
j := PARENT[j]; return(j);
}
Рассмотрим, как такую функцию можно реализовать на F#
let rec find x =
let index = Array.tryFindIndex ((=)x) parents.[0, *]
match index with
| Some(i) ->
match parents.[1, i] with
| p when p <> 0 -> find p
| _ -> x
| None -> x
Здесь мы объявляем рекурсивную функцию find, которая принимает текущую метку X. Массив PARRENT здесь не передается, так как он у нас уже есть в глобальном пространстве имен и функция его уже видит и может с ним работать.
Сначала функция пытается найти индекс метки в верхней строке (так как нужно найти его родителя, который расположен в нижней строке.
let index = Array.tryFindIndex ((=)x) parents.[0, *]
Если поиск увенчался успешно, то мы получаем его родителя и сравниваем с 0. Если родитель не равен 0, значит у этого нода тоже есть родитель и функция рекурсивно вызывает саму себя до тех пор, пока родитель не будет равен 0. Это будет означать, что мы нашли корневой нод множества.
match index with
| Some(i) ->
match parents.[1, i] with
| p when p <> 0 -> find p
| _ -> x
| None -> x
Следующая функция, которая нам понадобится, называется union. Она принимает две метки X и Y, а также массив PARENT. Эта структура модифицирует (если необходимо) PARENT для слияния подмножества, содержащего метку X, с множеством, содержащим метку Y. Процедура ищет корневые узлы обеих меток и если они не совпадают, то узел одной из метки назначается родительским узлом второй метки. Так происходит объединение двух множеств.
Построение объединения двух множеств.
X — метка, принадлежащая первому множеству.
Y — метка, принадлежащая второму множеству.
PARENT — массив, представляющии? структуру данных для объединения-поиска.
procedure union(X, Y, PARENT);
{
j := X;
k := Y;
while PARENT[j] <> 0
j := PARENT[j];
while PARENT[k]] <> 0
k := PARENT[k];
if j <> k then PARENT[k] := j;
}
Реализация на F# выглядит так
let union x y =
let j = find x
let k = find y
if j <> k then parents.[1, k-1] <- j
Обратите внимание, что здесь уже используется функция find, которую мы уже реализовали.
Также алгоритм требует дополнительных двух функций, которые называются neighbors и labels. Функция neighbors возвращает множество соседних точек слева и сверху (так как в нашем случае алгоритм работает по четырехсвязной компоненте) от заданного пикселя, а функция labels — возвращает множество меток, которые уже были присвоены заданному множеству пикселей, которые вернула функция neighbors. В нашем случае мы не будем реализовывать две эти функции, а сделаем только одну, которая объединит в себе обе функции и вернет найденные метки.
let neighbors_labels x y =
match (x, y) with
| (0, 0) -> []
| (0, _) -> [step1.[0, y-1]]
| (_, 0) -> [step1.[x-1, 0]]
| _ -> [step1.[x, y-1]; step1.[x-1, y]]
|> List.filter ((<>)0)
Забегая вперед сразу скажу, что массив step1, который использует функция уже существует в глобальном пространстве и содержит в себе результат обработки алгоритма при первом проходе. Хочу обратить особое внимание на дополнительный фильтр.
|> List.filter ((<>)0)
Он отсекает все результаты, которые равны 0. То есть, если метка содержит в себе 0, то мы имеем дело с точкой фонового изображения, которую обрабатывать не нужно. Это очень важный нюанс, который не упомянут в книге, из которой мы берем примеры, но тем не менее без такой проверки алгоритм работать не будет.
Постепенно, шаг за шагом мы приближаемся с самой сути алгоритма. Давайте еще раз посмотрим на изображение, которое нам нужно будет обработать.
Figure 5: Исходное бинарное изображение
\begin{matrix}
1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 \\
1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 \\
0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 \\
1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\
1 & 1 & 0 & 1 & 0 & 1 & 1 & 1
\end{matrix}
Перед обработкой создадим пустой массив step1, в котором будет сохраняться результат первого прохода.
Figure 6: Массив step1 для хранение результатов первичной обработки
\begin{matrix}
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Рассмотрим первые несколько шагов первичной обработки данных (только первые три строчки исходного бинарного изображения).
Перед тем, как пошагово рассмотреть алгоритм, посмотрим на псевдокод, которые объясняет общий принцип работы.
Поиск связных компонент на бинарном изображении.
B — исходное бинарное изображение.
LB — выходное маркированное изображение.
procedure classical_with_union-find(B, LB);
{
“Инициализация структур данных.” initialize();
“На проходе 1 каждои? строке L изображения присваиваются начальные значения меток.”
for L := 0 to MaxRow
{
“Инициализация всех меток в строке L нулевыми значениями”
for P := 0 to MaxCol
LB[L,P] := 0;
“Обработка строки L.”
for P := 0 to MaxCol
if B[L,P] == 1 then
{
A := prior_neighbors(L,P);
if isempty(A)
then {M := label; label := label + 1;};
else M := min(labels(A));
LB[L,P] := M;
for X in labels(A) and X <> M
union(M, X, PARENT);
}
}
“На проходе 2 метки, обнаруженные на проходе 1, заменяются метками соответствующих классов эквивалентности.”
for L := 0 to MaxRow
for P := 0 to MaxCol
if B[L, P] == 1
then LB[L,P] := find(LB[L,P], PARENT);
};
Шаг за шагом рассмотрим состояние массива LB (или step1) после каждого кадра алгоритма (первый проход).
Figure 7: Шаг 1. Точка (0,0), label = 1
\begin{matrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Figure 8: Шаг 2. Точка (1,0), label = 1
\begin{matrix}
1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Figure 9: Шаг 2. Точка (2,0), label = 1
\begin{matrix}
1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Figure 10: Шаг 4. Точка (3,0), label = 2
\begin{matrix}
1 & 1 & 0 & 2 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
Figure 11: Шаг последний, окончательный результат первого прохода
\begin{matrix}
1 & 1 & 0 & 2 & 2 & 2 & 0 & 3 \\
1 & 1 & 0 & 2 & 0 & 2 & 0 & 3 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\
4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\
0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\
6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\
6 & 6 & 0 & 4 & 0 & 7 & 7 & 3
\end{matrix}
Обратите внимание, что в результате первичной обработки исходного изображения у нас получилось два множества
Визуально это видно как соприкосновение меток 1 и 2 (координата точек (1,3) и (2,3)) и меток 3 и 7 (координата точек (7,7) и (7,6)). С точки зрения структуры данных для объединения-поиска получился такой результат.
Figure 12: Вычисленная структура-данных для объединения поиска
\begin{matrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 \\
0 & 1 & 0 & 0 & 0 & 0 & 3
\end{matrix}
После окончательно обработки изображения с помощью полученной структуры-данных мы получаем следующий результат.
Figure 13: Окончательный результат
\begin{matrix}
1 & 1 & 0 & 1 & 1 & 1 & 0 & 3 \\
1 & 1 & 0 & 1 & 0 & 1 & 0 & 3 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\
4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\
0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\
6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\
6 & 6 & 0 & 4 & 0 & 3 & 3 & 3
\end{matrix}
Теперь все связные компоненты у нас имеют уникальные метки и их можно использовать в последующих алгоритма для обработки.
Реализация кода на F# выглядит следующим образом
let markingOfConnectedComponents matrix =
// up to 10 markers
let parents = Array2D.init 2 10 (fun x y -> if x = 0 then y+1 else 0)
// create a zero initialized copy
let step1 = (Matrix.cloneO matrix).values
let rec find x =
let index = Array.tryFindIndex ((=)x) parents.[0, *]
match index with
| Some(i) ->
match parents.[1, i] with
| p when p <> 0 -> find p
| _ -> x
| None -> x
let union x y =
let j = find x
let k = find y
if j <> k then parents.[1, k-1] <- j
// returns up and left neighbors of pixel
let neighbors_labels x y =
match (x, y) with
| (0, 0) -> []
| (0, _) -> [step1.[0, y-1]]
| (_, 0) -> [step1.[x-1, 0]]
| _ -> [step1.[x, y-1]; step1.[x-1, y]]
|> List.filter ((<>)0)
let mutable label = 0
matrix.values
|> Array2D.iteri (fun x y v ->
if v = 1 then
let n = neighbors_labels x y
let m = if n.IsEmpty then
label <- label + 1
label
else
n |> List.min
n |> List.iter (fun v -> if v <> m then union m v)
step1.[x, y] <- m)
let step2 = matrix.values
|> Array2D.mapi (fun x y v ->
if v = 1 then step1.[x, y] <- find step1.[x, y]
step1.[x, y])
{ values = step2 }
Построчное объяснение кода уже не имеет смысла, так как все было рассказано выше. Здесь можно просто сопоставить код F# с псевдокодом, чтобы стало понятно, как он работает.
Сравнительный анализ алгоритмов
Давайте сравним скорость обработки данных обоими алгоритмами (рекурсивный и построчный).
let a = array2D [[1;1;0;1;1;1;0;1]
[1;1;0;1;0;1;0;1]
[1;1;1;1;0;0;0;1]
[0;0;0;0;0;0;0;1]
[1;1;1;1;0;1;0;1]
[0;0;0;1;0;1;0;1]
[1;1;0;1;0;0;0;1]
[1;1;0;1;0;1;1;1]]
let A = Matrix.ofArray2D a
let t1 = System.Diagnostics.Stopwatch.StartNew()
let R1 = Algorithms.markingOfConnectedComponents A
t1.Stop()
let t2 = System.Diagnostics.Stopwatch.StartNew()
let R2 = Algorithms.recMarkingOfConnectedComponents A
t2.Stop()
printfn "origin =\n %A" A.values
printfn "markers =\n %A" R1.values
printfn "rec markers =\n %A" R2.values
printfn "elapsed lines = %O" t1.Elapsed
printfn "elapsed recurcive = %O" t2.Elapsed
origin =
[[1; 1; 0; 1; 1; 1; 0; 1]
[1; 1; 0; 1; 0; 1; 0; 1]
[1; 1; 1; 1; 0; 0; 0; 1]
[0; 0; 0; 0; 0; 0; 0; 1]
[1; 1; 1; 1; 0; 1; 0; 1]
[0; 0; 0; 1; 0; 1; 0; 1]
[1; 1; 0; 1; 0; 0; 0; 1]
[1; 1; 0; 1; 0; 1; 1; 1]]
markers =
[[1; 1; 0; 1; 1; 1; 0; 3]
[1; 1; 0; 1; 0; 1; 0; 3]
[1; 1; 1; 1; 0; 0; 0; 3]
[0; 0; 0; 0; 0; 0; 0; 3]
[4; 4; 4; 4; 0; 5; 0; 3]
[0; 0; 0; 4; 0; 5; 0; 3]
[6; 6; 0; 4; 0; 0; 0; 3]
[6; 6; 0; 4; 0; 3; 3; 3]]
rec markers =
[[2; 2; 0; 2; 2; 2; 0; 3]
[2; 2; 0; 2; 0; 2; 0; 3]
[2; 2; 2; 2; 0; 0; 0; 3]
[0; 0; 0; 0; 0; 0; 0; 3]
[4; 4; 4; 4; 0; 5; 0; 3]
[0; 0; 0; 4; 0; 5; 0; 3]
[6; 6; 0; 4; 0; 0; 0; 3]
[6; 6; 0; 4; 0; 3; 3; 3]]
elapsed lines = 00:00:00.0081837
elapsed recurcive = 00:00:00.0038338
Как видно, на таком примере скорость работы рекурсивного алгоритма существенно превышает скорость построчного алгоритма. Но все меняется как только мы начинаем обрабатывать картинку, залитую сплошным цветом и для наглядности также увеличим ее размеры до 100х100 пикселей.
let a = Array2D.create 100 100 1
let A = Matrix.ofArray2D a
let t1 = System.Diagnostics.Stopwatch.StartNew()
let R1 = Algorithms.markingOfConnectedComponents A
t1.Stop()
printfn "elapsed lines = %O" t1.Elapsed
let t2 = System.Diagnostics.Stopwatch.StartNew()
let R2 = Algorithms.recMarkingOfConnectedComponents A
t2.Stop()
printfn "elapsed recurcive = %O" t2.Elapsed
elapsed lines = 00:00:00.0131790
elapsed recurcive = 00:00:00.2632489
Как видим, рекурсивный алгоритм уже в 25 раз работает медленнее линейного. Давайте увеличим размер картинки до 200х200 пикселей.
elapsed lines = 00:00:00.0269896
elapsed recurcive = 00:00:06.1033132
Разница уже во много сотен раз. Отмечу, что уже при размере 300х300 пикселей рекурсивный алгоритм вызывает переполнение стека и программа аварийно завершает свою работу.
Итоги
В рамках данной статьи был рассмотрен один из базовых алгоритмов маркировки связных компонентов для обработки бинарных изображений на примере функционального языка F#. Здесь были приведены примеры реализации рекурсивного и классического алгоритмов, объяснен их принцип работы, произведен сравнительный анализ на конкретных примерах.
Исходный код, рассмотренный здесь, также можно посмотреть на гитхабе
MatrixAlgorithms
Надеюсь, статья была интересна тем, кто интересуется F# и алгоритмами по обработке изображений в частности.

