Логистическая регрессия является одним из статистических методов классификации с использованием линейного дискриминанта Фишера. Также она входит в топ часто используемых алгоритмов в науке о данных. В этой статье суть логистической регрессии описана так, что она станет понятна даже людям не очень близким к статистике.

В отличие от обычной регрессии, в методе логистической регрессии не производится предсказание значения числовой переменной исходя из выборки исходных значений. Вместо этого, значением функции является вероятность того, что данное исходное значение принадлежит к определенному классу. Для простоты, давайте предположим, что у нас есть только два класса (см. Множественная логистическая регрессия для задач с большим количеством классов) и вероятность, которую мы будем определять, вероятности того, что некоторое значение принадлежит классу "+". И конечно
вероятности того, что некоторое значение принадлежит классу "+". И конечно 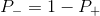 . Таким образом, результат логистической регрессии всегда находится в интервале [0, 1].
. Таким образом, результат логистической регрессии всегда находится в интервале [0, 1].
Основная идея логистической регрессии заключается в том, что пространство исходных значений может быть разделено линейной границей (т.е. прямой) на две соответствующих классам области. Итак, что же имеется ввиду под линейной границей? В случае двух измерений — это просто прямая линия без изгибов. В случае трех — плоскость, и так далее. Эта граница задается в зависимости от имеющихся исходных данных и обучающего алгоритма. Чтобы все работало, точки исходных данных должны разделяться линейной границей на две вышеупомянутых области. Если точки исходных данных удовлетворяют этому требованию, то их можно назвать линейно разделяемыми. Посмотрите на изображение.

Указанная разделяющая плоскость называется линейным дискриминантом, так как она является линейной с точки зрения своей функции, и позволяет модели производить разделение, дискриминацию точек на различные классы.
Но каким образом используется линейная граница в методе логистической регрессии для количественной оценки вероятности принадлежности точек данных к определенному классу?
Во-первых, давайте попробуем понять геометрический подтекст «разделения» исходного пространства на две области. Возьмем для простоты (в отличие от показанного выше ?3-мерного графика) две исходные переменные -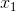 и
и 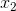 , тогда функция, соответствующая границе, примет вид:
, тогда функция, соответствующая границе, примет вид:
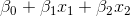
Рассмотрим точку . Подставляя значения
. Подставляя значения 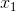 и
и 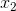 в граничную функцию, получим результат
в граничную функцию, получим результат 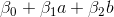 . Теперь, в зависимости от положения
. Теперь, в зависимости от положения  следует рассмотреть три варианта:
следует рассмотреть три варианта:
Итак, мы имеем функцию, с помощью которой возможно получить значение в пределах (-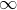 ,
,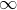 ) имея точку исходных данных. Но каким образом преобразовать полученное значение в вероятность
) имея точку исходных данных. Но каким образом преобразовать полученное значение в вероятность  , пределы которой [0, 1]? Ответ — с помощью функции отношения шансов (OR).
, пределы которой [0, 1]? Ответ — с помощью функции отношения шансов (OR).
Обозначим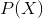 вероятностью происходящего события
вероятностью происходящего события 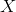 . Тогда, отношение шансов (
. Тогда, отношение шансов (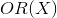 ) определяется из
) определяется из 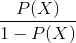 , а это — отношение вероятностей того, произойдет ли событие или не произойдет. Очевидно, что вероятность и отношение шансов содержат одинаковую информацию. Но, в то время как
, а это — отношение вероятностей того, произойдет ли событие или не произойдет. Очевидно, что вероятность и отношение шансов содержат одинаковую информацию. Но, в то время как 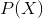 находится в пределах от 0 до 1,
находится в пределах от 0 до 1, 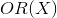 находится в пределах от 0 до
находится в пределах от 0 до 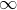 .
.
Это значит, что необходимо еще одно действие, так как используемая нами граничная функция выдает значения от -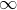 до
до 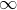 . Далее следует вычислить логарифм
. Далее следует вычислить логарифм 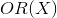 , что называется логарифмом отношения шансов. В математическом смысле,
, что называется логарифмом отношения шансов. В математическом смысле, 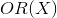 имеет пределы от 0 до
имеет пределы от 0 до 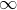 , а
, а  — от -
— от -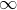 до
до 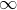 .
.
Таким образом, мы получили способ интерпретации результатов, подставленных в граничную функцию исходных значений. В используемой нами модели граничная функция определяет логарифм отношения шансов класса "+". В сущности, в нашем двухмерном примере, при наличии точки , алгоритм логистической регрессии будет выглядеть следующим образом:
, алгоритм логистической регрессии будет выглядеть следующим образом:
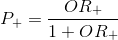
Получив значение в шаге 1, можно объединить шаги 2 и 3:
в шаге 1, можно объединить шаги 2 и 3:
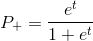
Правая часть уравнения, указанного выше, называется логистической функцией. Отсюда и название, данное этой модели обучения.
Остался не отвеченным вопрос: «Каким образом обучается граничная функция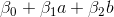 ?» Математическая основа этого выходит за рамки статьи, но общая идея заключается в следующем:
?» Математическая основа этого выходит за рамки статьи, но общая идея заключается в следующем:
Рассмотрим функцию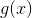 , где
, где 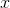 — точка данных обучающей выборки. В простой форме
— точка данных обучающей выборки. В простой форме 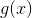 можно описать так:
можно описать так:
Функция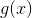 проводит количественную оценку вероятности того, что точка обучающей выборки классифицируется моделью правильным образом. Поэтому, среднее значение для всей обучающей выборки показывает вероятность того, что случайная точка данных будет корректно классифицирована системой, независимо от возможного класса.
проводит количественную оценку вероятности того, что точка обучающей выборки классифицируется моделью правильным образом. Поэтому, среднее значение для всей обучающей выборки показывает вероятность того, что случайная точка данных будет корректно классифицирована системой, независимо от возможного класса.
Скажем проще — механизм обучения логистической регрессии старается максимизировать среднее значение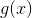 . А название этого метода — метод максимального правдоподобия. Если вы не математик, то вы сможете понять каким образом происходит оптимизация, только если у вас есть хорошее представление о том, что именно оптимизируется.
. А название этого метода — метод максимального правдоподобия. Если вы не математик, то вы сможете понять каким образом происходит оптимизация, только если у вас есть хорошее представление о том, что именно оптимизируется.

Основная идея логистической регрессии
В отличие от обычной регрессии, в методе логистической регрессии не производится предсказание значения числовой переменной исходя из выборки исходных значений. Вместо этого, значением функции является вероятность того, что данное исходное значение принадлежит к определенному классу. Для простоты, давайте предположим, что у нас есть только два класса (см. Множественная логистическая регрессия для задач с большим количеством классов) и вероятность, которую мы будем определять,
 вероятности того, что некоторое значение принадлежит классу "+". И конечно
вероятности того, что некоторое значение принадлежит классу "+". И конечно 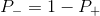 . Таким образом, результат логистической регрессии всегда находится в интервале [0, 1].
. Таким образом, результат логистической регрессии всегда находится в интервале [0, 1].Основная идея логистической регрессии заключается в том, что пространство исходных значений может быть разделено линейной границей (т.е. прямой) на две соответствующих классам области. Итак, что же имеется ввиду под линейной границей? В случае двух измерений — это просто прямая линия без изгибов. В случае трех — плоскость, и так далее. Эта граница задается в зависимости от имеющихся исходных данных и обучающего алгоритма. Чтобы все работало, точки исходных данных должны разделяться линейной границей на две вышеупомянутых области. Если точки исходных данных удовлетворяют этому требованию, то их можно назвать линейно разделяемыми. Посмотрите на изображение.

Указанная разделяющая плоскость называется линейным дискриминантом, так как она является линейной с точки зрения своей функции, и позволяет модели производить разделение, дискриминацию точек на различные классы.
Если невозможно произвести линейное разделение точек в исходном пространстве, стоит попробовать преобразовать векторы признаков в пространство с большим количеством измерений, добавив дополнительные эффекты взаимодействия, члены более высокой степени и т.д. Использование линейного алгоритма в таком пространстве дает определенные преимущества для обучения нелинейной функции, поскольку граница становится нелинейной при возврате в исходное пространство.
Но каким образом используется линейная граница в методе логистической регрессии для количественной оценки вероятности принадлежности точек данных к определенному классу?
Как происходит разделение
Во-первых, давайте попробуем понять геометрический подтекст «разделения» исходного пространства на две области. Возьмем для простоты (в отличие от показанного выше ?3-мерного графика) две исходные переменные -
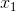 и
и 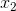 , тогда функция, соответствующая границе, примет вид:
, тогда функция, соответствующая границе, примет вид: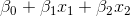
Важно отметить, что ии
являются исходными переменными, а выходная переменная не является частью исходного пространства в отличие от метода линейной регрессии.
Рассмотрим точку
 . Подставляя значения
. Подставляя значения 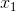 и
и 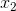 в граничную функцию, получим результат
в граничную функцию, получим результат 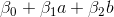 . Теперь, в зависимости от положения
. Теперь, в зависимости от положения  следует рассмотреть три варианта:
следует рассмотреть три варианта: лежит в области, ограниченной точками класса "+". Тогда
лежит в области, ограниченной точками класса "+". Тогда 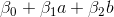 , будет положительной, находясь где-то в пределах (0,
, будет положительной, находясь где-то в пределах (0,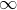 ). С математической точки зрения, чем больше величина этого значения, тем больше расстояние между точкой и границей. А это означает большую вероятность того, что
). С математической точки зрения, чем больше величина этого значения, тем больше расстояние между точкой и границей. А это означает большую вероятность того, что  принадлежит классу "+". Следовательно,
принадлежит классу "+". Следовательно,  будет находиться в пределах (0,5, 1].
будет находиться в пределах (0,5, 1]. лежит в области, ограниченной точками класса "-". Теперь,
лежит в области, ограниченной точками класса "-". Теперь, 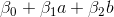 будет отрицательной, находясь в пределах (-
будет отрицательной, находясь в пределах (-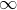 , 0). Но, как и в случае с положительным значением, чем больше величина выходного значения по модулю, тем больше вероятность, что
, 0). Но, как и в случае с положительным значением, чем больше величина выходного значения по модулю, тем больше вероятность, что  принадлежит классу "-", и
принадлежит классу "-", и  находится в интервале [0, 0.5).
находится в интервале [0, 0.5). лежит на самой границе. В этом случае,
лежит на самой границе. В этом случае, 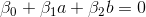 . Это означает, что модель действительно не может определить, принадлежит ли
. Это означает, что модель действительно не может определить, принадлежит ли  к классу "+" или к классу "-". И в результате,
к классу "+" или к классу "-". И в результате,  будет равняться 0,5.
будет равняться 0,5.
Итак, мы имеем функцию, с помощью которой возможно получить значение в пределах (-
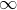 ,
,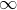 ) имея точку исходных данных. Но каким образом преобразовать полученное значение в вероятность
) имея точку исходных данных. Но каким образом преобразовать полученное значение в вероятность  , пределы которой [0, 1]? Ответ — с помощью функции отношения шансов (OR).
, пределы которой [0, 1]? Ответ — с помощью функции отношения шансов (OR).Обозначим
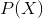 вероятностью происходящего события
вероятностью происходящего события 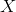 . Тогда, отношение шансов (
. Тогда, отношение шансов (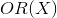 ) определяется из
) определяется из 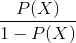 , а это — отношение вероятностей того, произойдет ли событие или не произойдет. Очевидно, что вероятность и отношение шансов содержат одинаковую информацию. Но, в то время как
, а это — отношение вероятностей того, произойдет ли событие или не произойдет. Очевидно, что вероятность и отношение шансов содержат одинаковую информацию. Но, в то время как 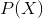 находится в пределах от 0 до 1,
находится в пределах от 0 до 1, 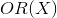 находится в пределах от 0 до
находится в пределах от 0 до 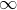 .
.Это значит, что необходимо еще одно действие, так как используемая нами граничная функция выдает значения от -
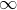 до
до 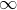 . Далее следует вычислить логарифм
. Далее следует вычислить логарифм 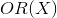 , что называется логарифмом отношения шансов. В математическом смысле,
, что называется логарифмом отношения шансов. В математическом смысле, 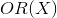 имеет пределы от 0 до
имеет пределы от 0 до 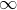 , а
, а  — от -
— от -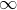 до
до 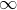 .
.Таким образом, мы получили способ интерпретации результатов, подставленных в граничную функцию исходных значений. В используемой нами модели граничная функция определяет логарифм отношения шансов класса "+". В сущности, в нашем двухмерном примере, при наличии точки
 , алгоритм логистической регрессии будет выглядеть следующим образом:
, алгоритм логистической регрессии будет выглядеть следующим образом:- Шаг 1. Вычислить значение
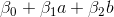 граничной функции (или, как вариант, функцию отношения шансов). Для простоты обозначим эту величину
граничной функции (или, как вариант, функцию отношения шансов). Для простоты обозначим эту величину  .
. - Шаг 2. Вычислить отношение шансов:
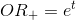 . (так как
. (так как  является логарифмом ).
является логарифмом ). - Шаг 3. Имея значение
 , вычислить
, вычислить  с помощью простой зависимости.
с помощью простой зависимости.
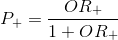
Получив значение
 в шаге 1, можно объединить шаги 2 и 3:
в шаге 1, можно объединить шаги 2 и 3: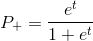
Правая часть уравнения, указанного выше, называется логистической функцией. Отсюда и название, данное этой модели обучения.
Как обучается функция
Остался не отвеченным вопрос: «Каким образом обучается граничная функция
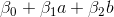 ?» Математическая основа этого выходит за рамки статьи, но общая идея заключается в следующем:
?» Математическая основа этого выходит за рамки статьи, но общая идея заключается в следующем:Рассмотрим функцию
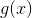 , где
, где 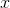 — точка данных обучающей выборки. В простой форме
— точка данных обучающей выборки. В простой форме 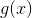 можно описать так:
можно описать так:еслиявляется частью класса "+",
(здесь
— выходное значение, полученное из модели логистической регрессии). Если
является частью класса "-",
.
Функция
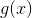 проводит количественную оценку вероятности того, что точка обучающей выборки классифицируется моделью правильным образом. Поэтому, среднее значение для всей обучающей выборки показывает вероятность того, что случайная точка данных будет корректно классифицирована системой, независимо от возможного класса.
проводит количественную оценку вероятности того, что точка обучающей выборки классифицируется моделью правильным образом. Поэтому, среднее значение для всей обучающей выборки показывает вероятность того, что случайная точка данных будет корректно классифицирована системой, независимо от возможного класса. Скажем проще — механизм обучения логистической регрессии старается максимизировать среднее значение
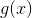 . А название этого метода — метод максимального правдоподобия. Если вы не математик, то вы сможете понять каким образом происходит оптимизация, только если у вас есть хорошее представление о том, что именно оптимизируется.
. А название этого метода — метод максимального правдоподобия. Если вы не математик, то вы сможете понять каким образом происходит оптимизация, только если у вас есть хорошее представление о том, что именно оптимизируется.Конспект
- Логистическая регрессия — одно из статистических методов классификации с использованием линейного дискриминанта Фишера.
- Значением функции является вероятность того, что данное исходное значение принадлежит к определенному классу.
- механизм обучения логистической регрессии старается максимизировать среднее значение
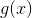 .
.


Dreamastiy
Спасибо за статью.
Интересно было бы почитать про многоклассовый логит.
Стоило упомянуть (поправьте, пожалуйста, если я ошибаюсь), что оценки максимального правдоподобия логита не существует в случае идеальной линейной разделимости исходных данных на классы (ситуация которая приведена в качестве примера в статье).
NotImplemented
Вы, очевидно, имеете ввиду мультиномиальную регрессию. Её можно построить, например, с помощью n-1 (n — число классов) независимых логистических регрессий, выбрав один класс в качестве базового (допустим первый). То есть, найти коэффициенты (беты) логарифма отношения вероятности того, что объект принадлежит в второму, третьему, ..., n-1 классу к вероятности того, что объект принадлежит первому. Получится n-1 комплект коэффициентов.