Это — специальная рубрика Нового физтеха ИТМО. Здесь учёные, преподаватели и студенты физико-технического факультета размышляют о науке, учебном процессе и трудовых буднях.

Капля, падающая на поверхность жидкости, исчезает быстро, но не мгновенно. Слияние капли с жидкостью задерживается из-за воздуха, выходящего из промежуточного слоя. Эффект можно пронаблюдать в фонтане, раковине на кухне и даже стакане с кофе.
 Капля в чашке кофе
Капля в чашке кофе
При сближении капли с поверхностью жидкости воздух в промежуточном слое не успевает выйти наружу. Давление возрастает, капля теряет свою скорость и может даже отскочить вверх. Но с каждым разом она подскакивает все ниже, так как часть энергии рассеивается благодаря воздействию внешних сил. Из промежуточного выходит все больше воздуха, и когда его толщина становится критической, водяной шарик сливается с жидкостью из-за сил молекулярного взаимодействия.
Интересен тот факт, что каплю можно заставить прыгать, если непрерывно подводить к ней потерянную энергию — например, с помощью колебаний водной поверхности. Жидкость будет выталкивать каплю вверх еще до того, как истончится воздушный слой.
Установка, необходимая для наблюдения за прыгающими каплями, достаточно проста. Она состоит из возбудителя колебаний и генератора капель. Роль первого может играть динамик, на который установлена ванночка с мыльным раствором или силиконовым маслом. В качестве второго подойдет обычная зубочистка. Вот пример собранного нами аппарата:
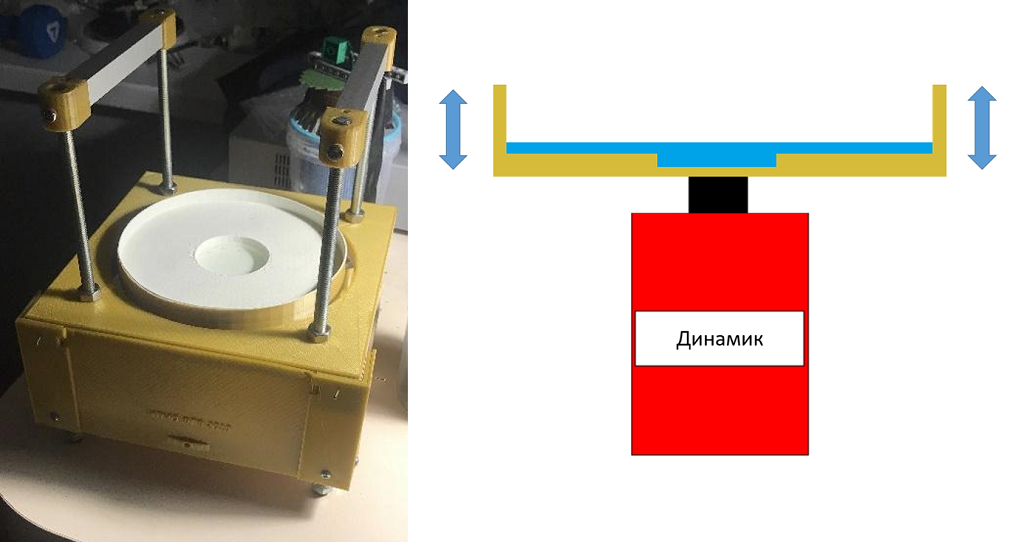
Корпус установки, напечатанный на 3D-принтере, и её схема
Капля, упавшая в ванночку, начнет «левитировать» только при определенной частоте и амплитуде колебаний динамика — эти параметры определяются экспериментально. Но есть основное условие: амплитуда должна быть достаточной для подбрасывания капли, но недостаточной для возникновения ряби Фарадея. Это — стоячие волны на поверхности жидкости, которые её дестабилизируют.
На способность водяного шарика подпрыгивать также влияет его размер. Он определяет минимальную амплитуду, необходимую для достижения эффекта. Чем меньше капля, тем меньшая амплитуда требуется для отскока — то есть капля способна продолжительно прыгать в большем диапазоне амплитуд и частот.

Рябь Фарадея
Что интересно, капли могут не только подпрыгивать. Они способны двигаться по определённым траекториям и взаимодействовать друг с другом. Явление обусловлено волнами, которые шарики генерируют при каждом отскоке от поверхности. Капли стремятся занять положение, соответствующее локальному минимуму потенциальной энергии, определяемому интерференцией порождаемых волн. Таких положений много, но расположены они на одинаковом расстоянии друг от друга — оно равно половине длины волны. Из одного положения каплю всегда можно «подтолкнуть» в другое.

Кристалл из двух стабильно прыгающих капель
Также bouncing droplets формируют устойчивые кристаллоподобные структуры. Например, правильные геометрические фигуры — треугольники, квадраты, пентагоны.
Волновой природой взаимодействия можно объяснить интересный эффект — масштабируемость кристалла при медленном изменении частоты. При её увеличении расстояние между водяными шариками растет, а при уменьшении, наоборот, сокращается.



Геометрические фигуры из капель
Фигуры являются достаточно «упругими», чтобы их можно было двигать, не разрушая структуру кристалла. Вот пример такого воздействия:

Перемещение кристалла
Если bouncing droplets находятся достаточно близко, и их размеры относительно велики, то они будут дрейфовать навстречу друг другу, образуя другое связанное состояние — кластер.

Кластеры
Большие капли тяжелые, поэтому они «продавливают» поверхность жидкости под собой. Возникает потенциальная яма, куда устремляются другие большие капли.
Система левитирующих капель — это не только красивый эффект макромира, но и явление, находящее отклик в квантовом мире.
Американский физик Джон Буш (John Bush) с коллегами из MIT в 2013 году наблюдал за так называемыми «ходячими» каплями, появляющимися вблизи порога Фарадея. Они «напрыгивают» на свою волну и двигаются по поверхности жидкости. Как и квантовые частицы, скорость которых не превышает скорости света, ходячие капли имеют аналогичное ограничение — скорость распространения волны в жидкости.
В свою очередь, Ива Кудер в 2006 году обнаружил, что капли проявляют свойства, характерные для волн. Физик направил водяные шарики на щель и сумел пронаблюдать явление дифракции — очень похожее на дифракцию электрона. Таким образом, bouncing droplets можно рассматривать как объекты (частицы), проявляющие корпускулярно-волновой дуализм.
И это лишь малая часть интересных экспериментов. Ученые также обнаружили следующие аналогии:
Таким образом, эти эксперименты, явления и зависимости представляют физический интерес и позволяют наблюдать квантоподобное поведение в масштабах капель жидкости.

Сегодня студенты бакалавриата на примерах с картинками покажут, как процесс подпрыгивания капель над поверхностью жидкости помогает понять квантовую механику.
Авторы проекта: Мария Цимоха, Анастасия Никитина, Владимир Игошин
Научный консультант: Дмитрий Соловьев
Физика процесса слияния капли
Капля, падающая на поверхность жидкости, исчезает быстро, но не мгновенно. Слияние капли с жидкостью задерживается из-за воздуха, выходящего из промежуточного слоя. Эффект можно пронаблюдать в фонтане, раковине на кухне и даже стакане с кофе.
 Капля в чашке кофе
Капля в чашке кофеПри сближении капли с поверхностью жидкости воздух в промежуточном слое не успевает выйти наружу. Давление возрастает, капля теряет свою скорость и может даже отскочить вверх. Но с каждым разом она подскакивает все ниже, так как часть энергии рассеивается благодаря воздействию внешних сил. Из промежуточного выходит все больше воздуха, и когда его толщина становится критической, водяной шарик сливается с жидкостью из-за сил молекулярного взаимодействия.
Как заставить капли прыгать
Интересен тот факт, что каплю можно заставить прыгать, если непрерывно подводить к ней потерянную энергию — например, с помощью колебаний водной поверхности. Жидкость будет выталкивать каплю вверх еще до того, как истончится воздушный слой.
Впервые явление прыгающих капель (bouncing droplets) было описано американским физиком Джерлом Уокером (Jearl Walker) в 1978 году. Но изучением динамики этого явления занялись лишь 30 лет спустя — французские исследователи из Университета Париж VII во главе с Ивом Кудером (Yves Couder).
Установка, необходимая для наблюдения за прыгающими каплями, достаточно проста. Она состоит из возбудителя колебаний и генератора капель. Роль первого может играть динамик, на который установлена ванночка с мыльным раствором или силиконовым маслом. В качестве второго подойдет обычная зубочистка. Вот пример собранного нами аппарата:

Корпус установки, напечатанный на 3D-принтере, и её схема
Капля, упавшая в ванночку, начнет «левитировать» только при определенной частоте и амплитуде колебаний динамика — эти параметры определяются экспериментально. Но есть основное условие: амплитуда должна быть достаточной для подбрасывания капли, но недостаточной для возникновения ряби Фарадея. Это — стоячие волны на поверхности жидкости, которые её дестабилизируют.
На способность водяного шарика подпрыгивать также влияет его размер. Он определяет минимальную амплитуду, необходимую для достижения эффекта. Чем меньше капля, тем меньшая амплитуда требуется для отскока — то есть капля способна продолжительно прыгать в большем диапазоне амплитуд и частот.

Рябь Фарадея
Что интересно, капли могут не только подпрыгивать. Они способны двигаться по определённым траекториям и взаимодействовать друг с другом. Явление обусловлено волнами, которые шарики генерируют при каждом отскоке от поверхности. Капли стремятся занять положение, соответствующее локальному минимуму потенциальной энергии, определяемому интерференцией порождаемых волн. Таких положений много, но расположены они на одинаковом расстоянии друг от друга — оно равно половине длины волны. Из одного положения каплю всегда можно «подтолкнуть» в другое.

Кристалл из двух стабильно прыгающих капель
Также bouncing droplets формируют устойчивые кристаллоподобные структуры. Например, правильные геометрические фигуры — треугольники, квадраты, пентагоны.
Волновой природой взаимодействия можно объяснить интересный эффект — масштабируемость кристалла при медленном изменении частоты. При её увеличении расстояние между водяными шариками растет, а при уменьшении, наоборот, сокращается.



Геометрические фигуры из капель
Фигуры являются достаточно «упругими», чтобы их можно было двигать, не разрушая структуру кристалла. Вот пример такого воздействия:

Перемещение кристалла
Если bouncing droplets находятся достаточно близко, и их размеры относительно велики, то они будут дрейфовать навстречу друг другу, образуя другое связанное состояние — кластер.

Кластеры
Большие капли тяжелые, поэтому они «продавливают» поверхность жидкости под собой. Возникает потенциальная яма, куда устремляются другие большие капли.
Эта яма преобладает над потенциальными ямами поверхностных волн. Поэтому для больших капель не характерен волновой тип взаимодействия.
Какое отношение капли имеют к квантовой механике
Система левитирующих капель — это не только красивый эффект макромира, но и явление, находящее отклик в квантовом мире.
Американский физик Джон Буш (John Bush) с коллегами из MIT в 2013 году наблюдал за так называемыми «ходячими» каплями, появляющимися вблизи порога Фарадея. Они «напрыгивают» на свою волну и двигаются по поверхности жидкости. Как и квантовые частицы, скорость которых не превышает скорости света, ходячие капли имеют аналогичное ограничение — скорость распространения волны в жидкости.
В свою очередь, Ива Кудер в 2006 году обнаружил, что капли проявляют свойства, характерные для волн. Физик направил водяные шарики на щель и сумел пронаблюдать явление дифракции — очень похожее на дифракцию электрона. Таким образом, bouncing droplets можно рассматривать как объекты (частицы), проявляющие корпускулярно-волновой дуализм.
И это лишь малая часть интересных экспериментов. Ученые также обнаружили следующие аналогии:
- Колебания капель в связанном состоянии и колебательное движение фононов в атоме кристалла;
- Вращательное движение капель и перемещение электронов по орбите.
Таким образом, эти эксперименты, явления и зависимости представляют физический интерес и позволяют наблюдать квантоподобное поведение в масштабах капель жидкости.
- Сайт Нового физтеха ИТМО
- Мы в Instagram, Facebook и Vk


vitalijlysanov
На поверхности воды с помощью стробоскопа можно наблюдать еще одни волны, так понял что волны образуются от поверхностного натяжения.
Эти волны тоже могут принимать участие в эффектах.
На напряжение подводимое к динамику можно включить светодиод, а что будет — ?
(Стробоскоп — это велосипедный фонарик в режиме меандра 50 гц)
BD9
Нет.
Стробоскоп.
С точки зрения КМ электроны по орбитам не перемещаются.
Про «колебательное движение фотонов в атоме кристалла» вообще не понял. Фотон есть также и волна. И при чём тут кристалл?
Yermack
там наверно имелись в виду фононы
itmo Автор
Да, фононы (автокоррект сработал, исправление уже внесли).
itmo Автор
О стробоскопе: будет казаться, что жидкость не колеблется, а замерла, при этом картина максимумов и минимумов будет перемещаться за каплей.