01.09.2020 16:11
Refridgerator 7 3800 Источник
Как известно, кривыми Безье нельзя построить дугу окружности или эллипса. В этой статье рассматриваются кривые, лишённые такого недостатка.



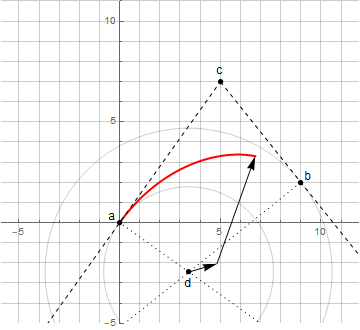
Кривые Безье


Логика построения кривых Безье хорошо понятна из следующей анимации:



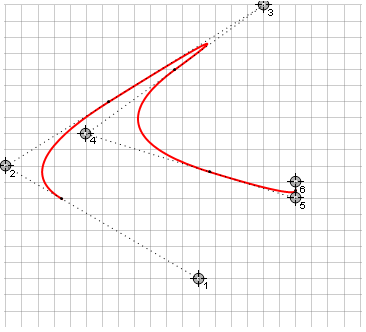
Чтобы получить формулу непосредственно из графического представления, достаточно определить вспомогательную функцию для линейной интерполяции между двумя точками, в которая при изменении параметра t от 0 до 1 возвращает промежуточные значения от a до b:

$mix(a,b,t) =a (1-t)+b t$

Примечание
В математике как-то не сложилось устойчивого названия для функции линейной интерполяции и в зависимости от сферы применения она может называться lerp, blend, mix и как-то ещё. К ней также относится и кривая Безье первого порядка.


С её помощью можно последовательно найти необходимые точки — сначала найти

$ac = mix(a, c, t)$

и

$cb = mix(с, b, t)$


а затем уже через них найти

$d = mix(ac, cb, t)$


При желании, можно подставить функции друг в друга и сократить — хотя это особо и не упростит вычисления, зато позволит обобщить кривые на произвольное количество опорных точек (через полиномы Бернштейна). В нашем случае получим

$d = a (1-t)^2+b t^2+2 c t (1-t)$


Увеличение порядка кривых достигается тривиально — исходные точки задаются не константно, а как результат интерполяции между n+1 других контрольных точек:


Примечание
В этих формулах в качестве точек могут выступать как комплексные числа, так и векторы произвольной размерности. Дальнейшие формулы будут корректными только для комплексных чисел.

Циркулярные кривые



Дуга окружности


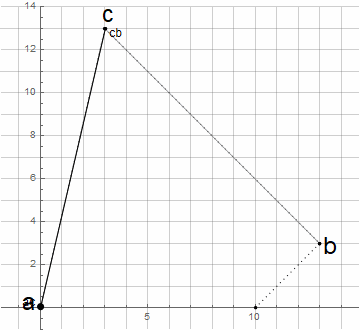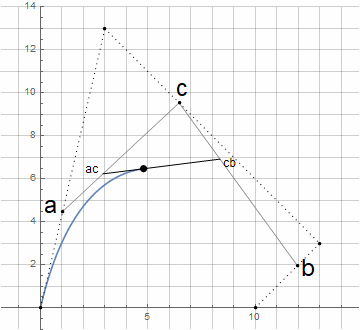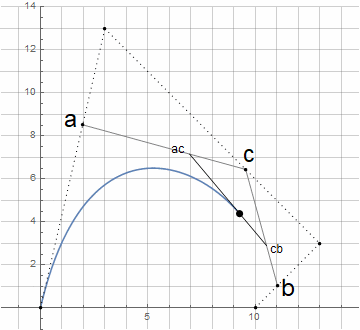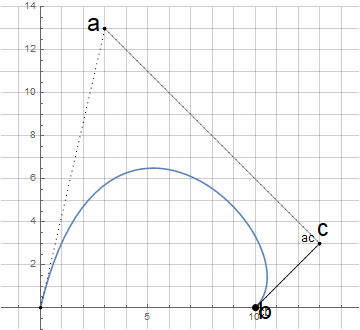
Чтобы похожим образом построить дугу окружности, необходимо определить соответствующую логику построения — по аналогии с черчением окружности циркулем.


Изначально нам неизвестен центр окружности d — он находится через пересечение перпендикуляров к касательным в точках a и b (далее узловых); сами же касательные задаются с помощью точки c (далее направляющей). Для построения произвольной дуги окружности (меньшей 180°) достаточно, чтобы расстояния от направляющей точки до узловых были одинаковыми.


Дуга эллипса


Построить дугу эллипса уже посложнее — потребуется два вектора, вращающихся в разные стороны (подробнее здесь)


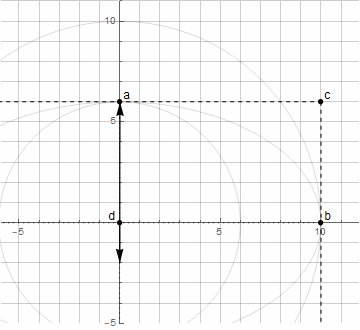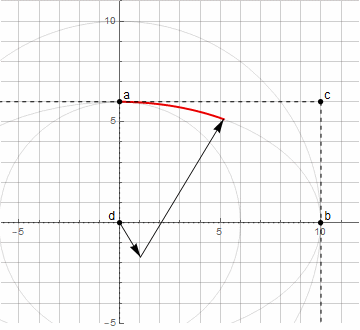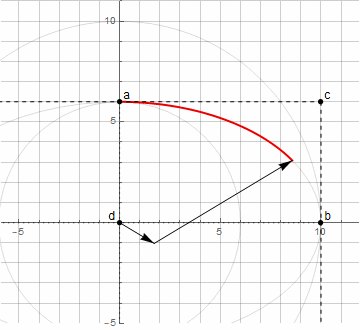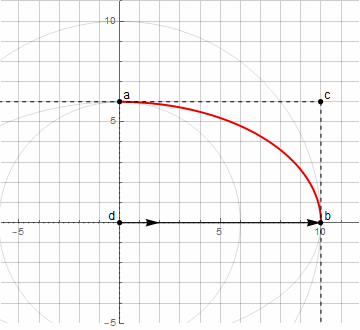
Используя озвученный выше способ нахождения точки d, мы уже не можем построить произвольную дугу эллипса — только лишь от 0° до 90° (в том числе и повёрнутую на некоторый угол).

Дуга гипотрохоиды


Задав условие, что в начале и конце черчения векторы должны лежать на одной прямой, мы получим дугу гипотрохоиды во всех остальных случаях. Это условие не случайно и (помимо однозначного определения кривой) гарантирует совпадение касательных в узловых точках. Как следствие, угловые пути, которые проходят оба вектора, станут разными, но в сумме по-прежнему будут давать 180°.


Как изменяется форма кривой в зависимости от положения направляющей точки, можно посмотреть на следующей анимации:



Алгоритм


Поскольку здесь мы имеем вращения на двумерной плоскости, математику построения этих кривых удобно описывать через комплексные числа.

1) находим точку пересечения нормалей касательных, проведённых от направляющей точки к узловым:

$d=\frac{(2 a-c) (c-b) a^*+ (2 b-c) (a-c) b^*-c (a-b) c^*}{(c-b)a^*+(a-c) b^*-(a-b) c^*}$

(здесь звёздочка означает комплексное сопряжение).

2) зная d, находим длины нормалей

$r_{\text{ad}}=\left| a-d\right|$

$r_{\text{bd}}=\left| b-d\right|$



и их сумму и разность

$r_m=\frac{1}{2} \left(r_{\text{ad}}+r_{\text{bd}}\right)$

$r_s=\frac{1}{2} \left(r_{\text{ad}}-r_{\text{bd}}\right)$



3) находим единичный вектор, от которого начинается построение

$v=\frac{a-d}{\left| a-d\right| }$


Примечание
в некоторых библиотеках для работы с комплексными числами и системах компьютерной алгебры для этого есть отдельная функция sign(x).


4) находим угловые пути, которые должны пройти каждый из векторов

$\phi _m=\arg \left(\frac{a-d}{b-d}\right)$

$\phi _s=\arg \left(-\frac{a-d}{b-d}\right)$


Примечание
При умножении векторов их длины умножаются, а углы — складываются. Здесь деление используется для противоположной задачи — найти разницу углов, т. е. угол между векторами.

Поскольку для функции аргумента длина вектора не играет роли, тот же результат можно получить и заменив деление умножением на комплексно сопряжённый вектор — такой вариант даже предпочтительнее, поскольку будет более численно устойчив на очень малых значениях из-за отсутствия деления; здесь же выбор в пользу деления сделан исключительно ради наглядности.

Здесь имеется ещё один крайне важный момент. Если бы мы сначала нашли углы для каждого вектора по отдельности, а потом бы считали разницу как

$\arg (a-d)-\arg (b-d)$


— результат не всегда был бы корректным из-за многозначности функции аргумента.

5) последовательно изменяя t от 0 до 1 с некоторым шагом, находим принадлежащую кривой точку по формуле

$d+v \left(r_m e^{-i t \phi _m}+r_s e^{-i t \phi _s}\right)$



Циркулярные сплайны


Так же, как и кривые Безье, эти кривые можно совмещать для кусочно-непрерывного построения сплайнов. Для обеспечения гладкости в узловых точках (стыковки) необходимо, чтобы узловая точка находилась на одной линии с двумя соседними направляющими точками. Для этого можно задавать узловые точки не явным образом, а через интерполяцию направляющих точек. Их также можно не задавать вообще, вычисляя полностью автоматически — например, как среднее между направляющих точек:



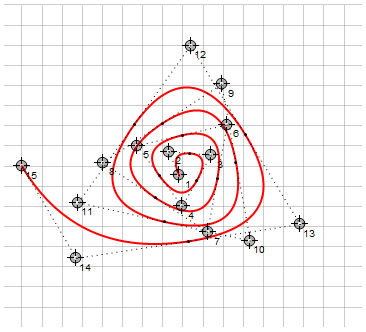
Справа для сравнения использован тот же подход с кривыми Безье 2-го порядка.

Замечания и нюансы


В отличие от кривых Безье, здесь кривая не всегда лежит внутри фигуры из линий, соединяющих контрольные точки, например


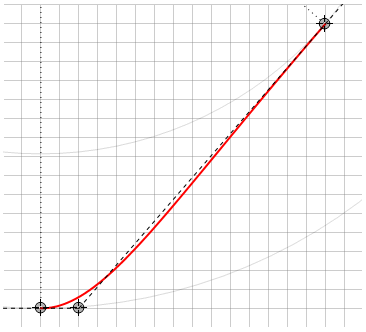
Кроме того, существует вырожденный случай, который необходимо обрабатывать отдельно — когда направляющая точка лежит на одной прямой с узловыми точками. При этом кривая вырождается в прямую, а при попытке вычислить точку d возникает деление на ноль.

У этих кривых также имеется ограничения на кривизну линии, поскольку в соответствии с алгоритмом выбирается наименьший путь следования и кривая не может обогнуть больше, чем 180°. Это приводит к тому, что при кусочно-непрерывной интерполяции могут возникать острые углы при определённом положении направляющих точек (справа — те же точки для Безье):



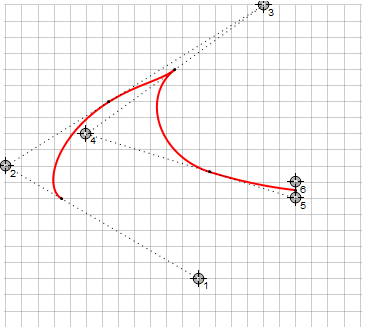
Заключение


Дальнейшим развитием рассмотренного метода построения кривых является увеличение количества векторов, участвующих в построении кривой и, соответственно, увеличение количества направляющих точек. Однако, в отличие от кривых Безье, повышение порядка здесь не является очевидным и требует отдельного вдумчивого размышления. Также возможны различные методы комбинации их с кривыми Безье — в частности, интерполяции центра окружности рисующих векторов.

Рассмотренный метод построения кривых также не является единственным, частным случаем которого являются дуги окружности и эллипса — как минимум, эллипс можно построить через пересечение прямых в параллелограмме (правда, в этом варианте автор потерпел неудачу). Возможно, что существуют и другие решения, в том числе и варианты описанного в статье — пишите в комментариях, если вам что-то известно на эту тему.

Исходный код статьи можно скачать на GitHub.