03.09.2020 09:38
Refridgerator 40 13000 Источник
На днях вышла статья, посвящённая разнице между квадратом со скруглёнными краями и «квадрокругом» — промежуточной фигурой между окружностью и квадратом, полученной из формулы cуперэллипса. Мнения читателей разделились — не все увидели разницу, а кто увидели — не все отдали предпочтение «правильному» варианту. И я подозреваю, почему: эти ваши квадрокруги — ненастоящие!




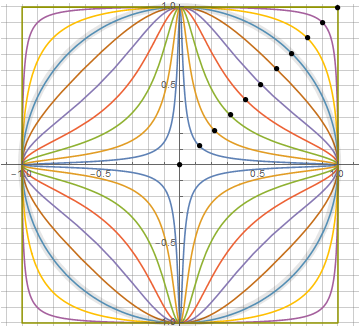
Альтернативное решение


Предпосылки
Некоторое время назад один мой близкий человек увлёкся рупоростроением и захотел построить рупор с круглым входом (для динамика), но прямоугольным выходом — из эстетических и практических соображений. Естественно, профиль должен перетекать из круга в квадрат достаточно плавно, чтобы не возникало излишних паразитных переотражений. Довольно быстро он нашёл формулу суперэллипса, однако результат его совершенно не вдохновил. При n от 1 до 2 углы были острыми, при n от 2 до бесконечности фигуры были больше похожи на квадраты со скруглёнными углами, чем на действительно промежуточные фигуры. И, поскольку квадрат получался лишь при стремлении n к бесконечности, совершенно непонятно было, на какой n останавливаться. 5? 10? 1000? А ещё при больших n формула становилась численно неустойчивой.

А ещё ему хотелось иметь формулу не параметрически заданную, а в полярных координатах.

В общем, он предложил мне подумать над альтернативным решением.

Моё решение (в полярных координатах) получилось таким:

$\rho =\sqrt{\frac{2}{1+\sqrt{1+\left(\frac{1}{k^4}-\frac{2}{k^2}\right) \sin ^2(2 \phi )}}}$


в которой параметр $k$ от 0 до 1 задаёт степень «оквадрачивания», причём линейно — определяя точку пересечения (k,k) фигуры с диагональю. Это значит, что можно однозначно определить наш квадрокруг через 3 точки. И да, при $k = 1$ мы имеем самый настоящий квадрат, с прямыми сторонами и острыми углами. Ну а круг, соответственно, получается при $k = \frac{1}{\sqrt{2}}$ (косинус 45°). Варианты получаемых фигур отражены на КДПВ.

Вы также можете обратить внимание, что в этой формуле нет таких хитростей, как функции остатка от деления, взятия/отбрасывания знака и прочего — как это требуется для суперэллипса. Всё честно, только стандартные математические функции, с которыми не возникнет сложности при дифференцировании или интегрировании. Кстати про интегрирование — при желании, можно найти и площадь этих фигур (через эллиптические интегралы):

$\frac{4 k^4 E\left(\frac{2 k^2-1}{k^4}\right)-4 \left(k^2-1\right)^2 K\left(\frac{2 k^2-1}{k^4}\right)}{2 k^2-1}$

Примечание
Эллиптические интегралы — это такие же функции, как и все остальные, вроде sin и cos. Похожее на операцию взятия первообразной название не должно вводить вас в заблуждение.


Развитие


Можно добавить больше вариативности полученным фигурам. Например, так:

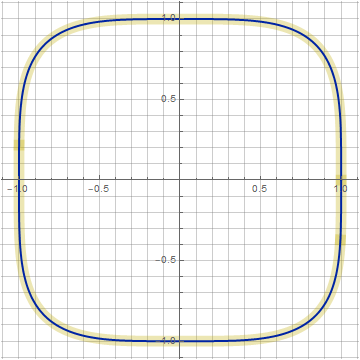
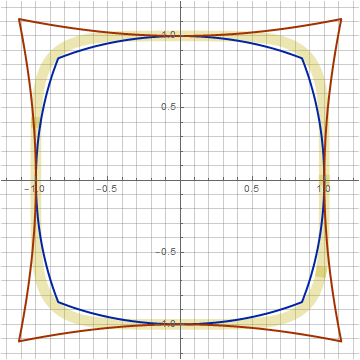
$\rho =\sqrt{\frac{1+\sqrt{\frac{(z-2)^2}{z^2}}}{1+\sqrt{1+\left(\frac{1}{k^4}-\frac{2}{k^2}\right) \sin^2(2\phi)+\left(\frac{4(1-z)}{z^2}\right)\cos^2(2 \phi)}}}$


Здесь у нас появился ещё один параметр z, позволяющий искажать фигуру не нарушая идеологию построения. С её помощью можно приблизить нашу фигуру к суперэллипсу (на графиках отображён жёлтым цветом). Например, при n=4 (k=0.266, z=0.1) совпадение почти идеальное:



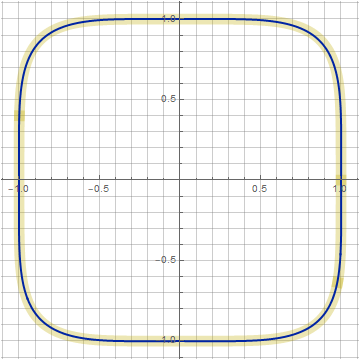
при более высоких n разница уже более ощутима (n=5, k=0.6, z=0.48):



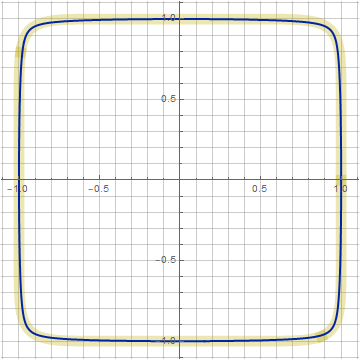
n=10, k=0.942, z=1.02:


И да, можно же пойти совсем радикальным способом! Такой дизайн иконок уж точно ни с чем не перепутаешь:



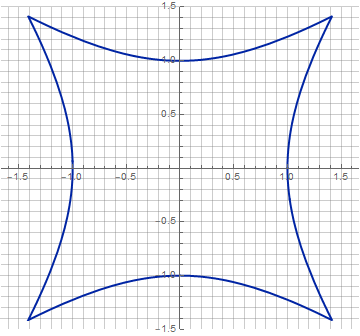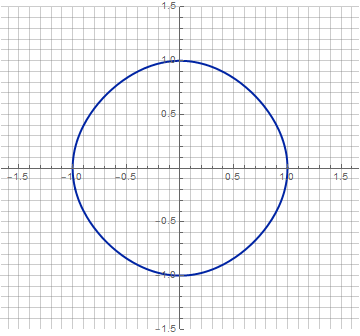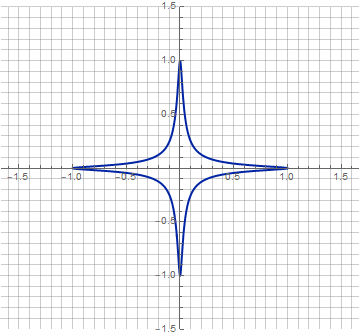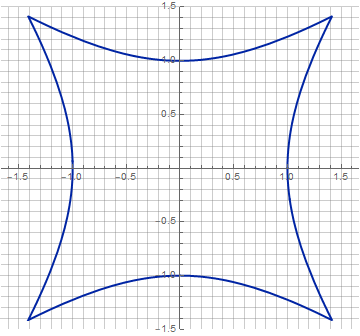
Ну и с анимацией тоже можно слегка пофантазировать:



Заключение


Если некий дизайнер некоторой фирмы с (необязательно) фруктовым логотипом хочет получить уникальный дизайн, пусть и не отличающийся принципиально от уже существующих решений — возможно, стоит попробовать поискать и запатентовать действительно новую формулу, а не привлекать давно известное решение, навешивая на него тонны маркетингового булшита. Особенно если это может сделать just for fun простой человек из глубинки без специального образования.

P.S. Исходники статьи здесь.

P.P.S. Через уравнение кривой в декартовых координатах первоначальная формула будет выглядеть как

$0=-2+\left(x^2+y^2\right) \left(1+\sqrt{1+\frac{\left(4-8 k^2\right) x^2 y^2}{k^4 \left(x^2+y^2\right)^2}}\right)$