18.12.2020 04:45
a_zamashchikova 6 2100 Источник

Мы в 2ГИС хотим облегчить пользовательскую поисковую рутину и потому стремимся предугадывать запросы пользователей. Под катом расскажем про то, как мы придумали алгоритм для персонализации интересных мест и что из этого вышло.


image


POI (point of interest) — маленькая круглая иконка на карте. Обозначает место или компанию, которые могут представлять интерес для пользователя.


image
Вот они — POI 2ГИС. У каждой рубрики своя иконка


Объекты POI — популярные у большинства городские объекты в разных рубриках. А хочется учитывать ещё и интересы каждого пользователя отдельно. Поэтому мы решили добавить на карту персонализированные POI, которые будут отвечать за это.


Удачно подобранные POI ещё и сокращают цепочку шагов поиска на карте. Обычно пользователь ищет что-то так: открыл приложение > ввёл поисковый запрос > просмотрел выдачу > открыл карточку объекта.


С персонализированными POI пользователь может без поискового запроса сориентироваться на карте и найти информацию: открыл приложение > увидел нужный POI на карте > открыл карточку объекта.


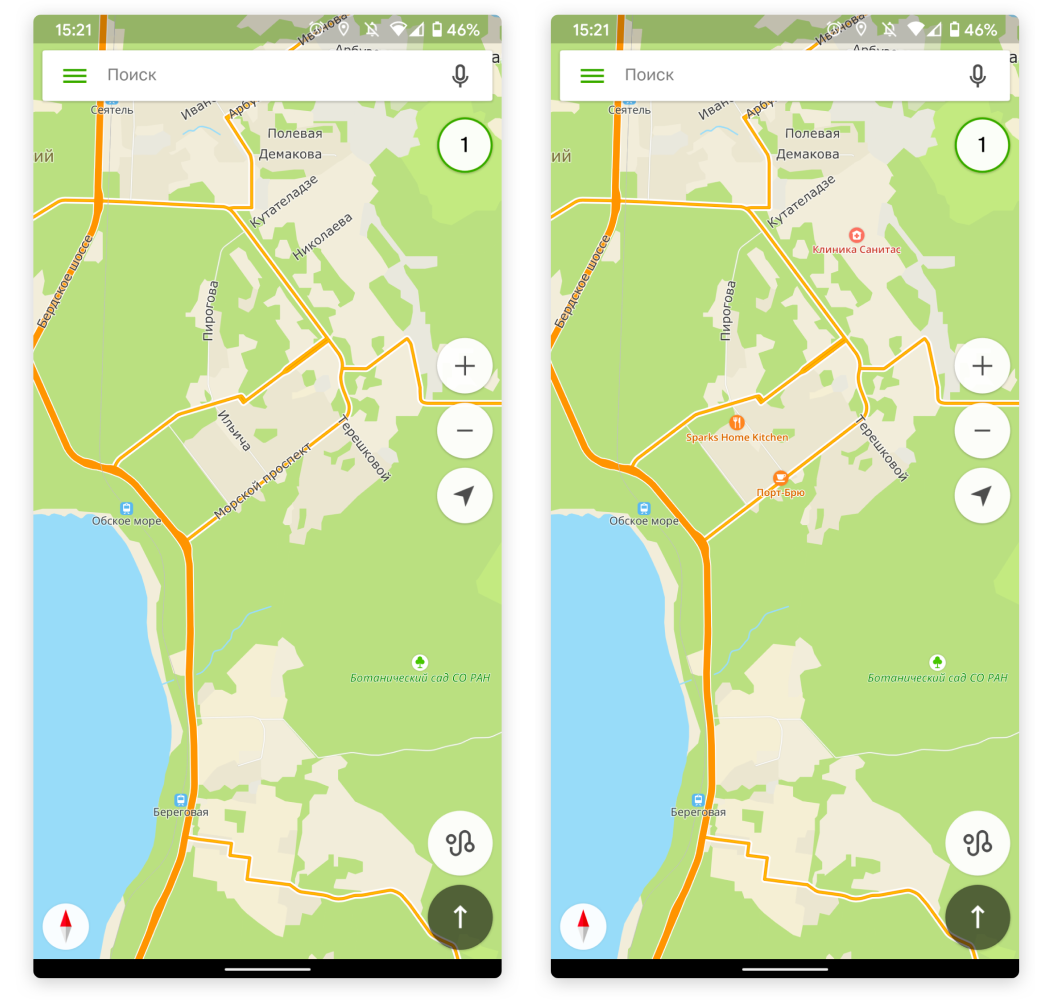
image
Карта без персонализированных POI и с ними — интересными для пользователя рестораном, кофейней и клиникой


Данные


В качестве потенциальных объектов для POI логично брать те, к которым пользователь уже проявлял интерес. А среди них искать такие, к которым он вернётся с наибольшей вероятностью. При этом желательно, чтобы объекты интересовали пользователя как можно дольше — чтобы он привык искать их на карте.


Но как классифицировать эти данные? Можно разметить выборку объектов, обогатить множеством признаков и применить бустинг или нейронные сети. Но можно пойти другим путём — и придумать эмпирическое правило.


Эмпирическое правило


У эмпирического правила есть и плюсы, и минусы. Да, это даст более слабое качество классификации. Но главное преимущество — мы можем быстро и легко проверить востребованность POI. Подготовка данных, обучение такой модели и её внедрение займёт значительно меньше времени, чем, например, бустинг. А если фича окажется успешной как для пользователя, так и для компании, мы всегда сможем переключиться на более сложные и затратные модели.


Для эмпирических моделей важен хороший контекст в предметной области. Исследуя поведение пользователей в продукте, мы выяснили, что вероятность повторного обращения пользователя к продукту (retention rate) имеет экспоненциальное распределение.


Такое свойство есть не только у retention rate продукта, но и у многих других явлений, связанных с повторным обращением — например, повторное обращение к объекту, как в нашем случае. Это знание помогло нам разработать алгоритмы по определению «домашнего» города для пользователя, краткосрочных и долгосрочных пользовательских интересов.


Первый алгоритм


Первым делом сформировали выборку вида

$X^{l}=(x_{i},y_{i})_{i=1}^{l}$


$x_{i} $ — n-мерный вектор признаков i-го объекта, а в качестве объекта классификации рассматриваем все объекты, которыми интересовался пользователь за определённое время до даты расчёта. В нашем случае это два месяца.

$y_{i} $ — класс i-го объекта — отклик, который принимает значение, равное 1, если пользователь посетил фирмы в контрольный период времени, и 0, если не посетил.


Так как нам важны объекты, которые будут долго интересны пользователю, то в качестве контрольного периода выбрали месяц через две недели после даты расчёта. Этот лаг в две недели нужен, чтобы не захватить в число успешных объекты мгновенного/краткосрочного интереса — те, которые пользователь ищет прямо в дату расчёта или рядом с ней, но не факт, что вернётся к ним. Успешными считаем объекты с y=1 — то есть те, к которым пользователь вернулся во время контрольного периода.


Правило $a:X\rightarrow Y$, которое множеству признаков объекта Х ставит в соответствие его класс Y, выглядит так:


$f(y|x)=\left\{\begin{matrix} \sum_{i=1}^{k}x_{i} \cdot exp\left ( \frac{i\cdot \beta}{k} \right )>\alpha ,y=1 \\иначе,y=0\end{matrix}\right., $


где k — общее количество дней (или любой другой единицы времени) в обучающей выборке.


$x_{i} $ равно 1, если в день с номером i пользователь интересовался объектом, иначе 0. ??Номер дня равен 1 в первый день обучающей выборки и k в последний.


$\beta $ — параметр, отвечающий за скорость изменения значимости дня взаимодействия с объектом по мере удаления от даты расчёта.


$\alpha $ — пороговое значение.


Идея в том, что чем дальше день, когда пользователь интересовался объектом, тем меньший вес будет у этого дня при оценке этого объекта. Параметры функции $\alpha $ и $\beta $ подбираются путём максимизации целевой переменной:


$\hat{\alpha },\hat{\beta }= \arg\max_{\alpha ,\beta }F\left ( f\left(y| x \right ) \right )$


где F — это F-мера с соответствующим соотношением желаемой точности и полноты модели. В этой задаче основной акцент на точности алгоритма, поэтому брали параметр $\gamma =0.5$.


$F_{\gamma }=\left ( 1+\gamma ^{2} \right )\cdot \frac{precision\cdot recall}{\gamma ^{2}*precision+recall}$


Результаты 1.0


Проверили алгоритм больше чем на 450 млн объектов. Среди них доля объектов с откликом, равным 1, составляет примерно 5%. Полнота алгоритма — 0.153, точность — 0.401, а F-мера $(\gamma =0.5)$ — 0.303.


Качество такого алгоритма может показаться недопустимо низким. Дело в том, что в число объектов для классификации входят объекты, которые мы не можем отнести к долгосрочным интересам на основе данных метрик — пользователи интересовались ими слишком мало, чтобы делать какие-то выводы.


Только 3% объектов интересовали пользователя больше двух дней за обучающий период. В этом нет ничего удивительного: туда входят объекты из сфер с низким retention. Таких много, они могут быть очень крупными — например, аптеки, бары или просто объекты, которые не заинтересовали пользователя.


Среди объектов с откликом, равным 1, такой процент выше — 22%. Это тоже мало, но объясняется большим периодом между посещениями объекта.


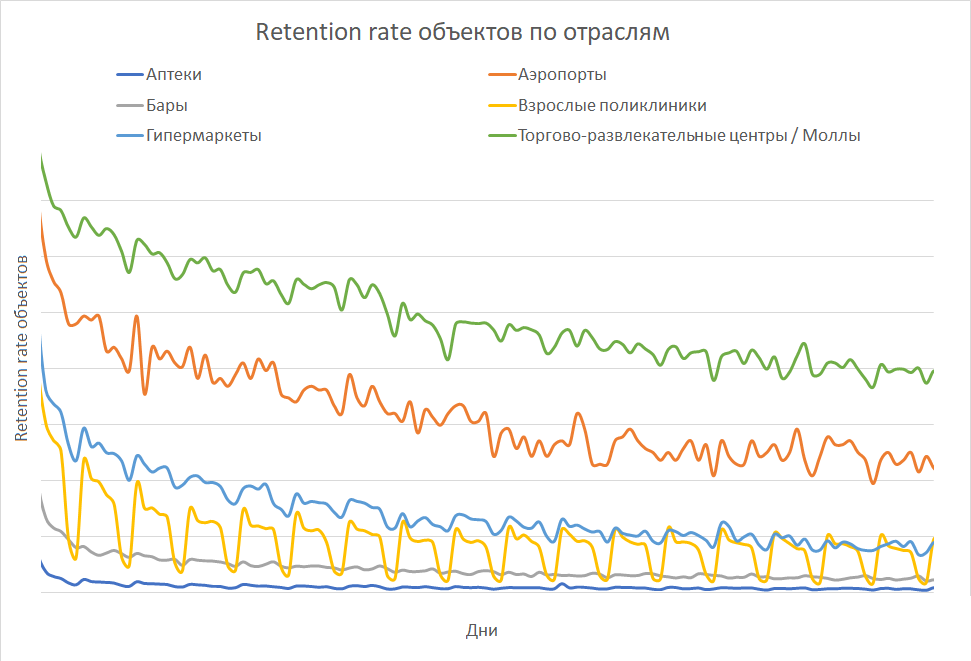
image


Если исключить такие объекты, то при тех же параметрах модели полнота вырастает с 0.153 до 0.684 при той же точности в 0.401, а F-мера с акцентом на точности становится равной 0.437 — классическая, конечно, выше.


Однако при таком виде модели остаётся ещё две проблемы. Во-первых, у пользователей разный уровень активности: кто-то пользуется приложением раз в день, а кто-то — раз в месяц. Поэтому использование общего порогового значения и одних параметров весовой функции может занижать качество классификации.


Во-вторых, у объектов может быть разная частота посещения в зависимости от их сферы деятельности. Например, за продуктами в гипермаркет пользователь ездит стабильно раз в неделю, в парикмахерскую ходит раз в месяц, а при простуде может посещать поликлинику так часто, как скажет врач. Так что мы можем упускать объекты с большими интервалами посещения.


Второй алгоритм


Чтобы учесть эти проблемы, мы добавили в функцию признак, показывающий максимальный период пользовательского интереса, и немного иначе учли интенсивность посещения объекта и его актуальность. Разделили пользователей на три группы по частоте посещения продукта. Для каждой из них подобрали свои параметры этой модели:


$f(y|x)=\left\{\begin{matrix} exp\left ( \frac{x_{1}\cdot \beta }{k} \right )\cdot \left ( \lambda x_{2}+\mu x_{3} \right ))>\alpha ,y=1 \\иначе,y=0\end{matrix}\right.,$


k — количество дней в обучающей выборке.


$x_{1} $— номер последнего дня взаимодействия пользователя с объектом (равен 1 в первый день обучающей выборки и k в последний).


$x_{2} $— количество дней взаимодействия пользователя с объектом в рассматриваемом периоде.


$x_{3} $— количество дней между первым и последним днём взаимодействия пользователя с объектом в рассматриваемом периоде.


$\alpha ,\beta, \lambda ,\mu $ — параметры функции, которые подбираются путём максимизации целевой переменной (в нашем случае это F-мера) аналогичным для первой модели образом.


Результаты 2.0


Оценили параметры и получили следующие результаты по кластерам пользователей.


Кластер Полнота Точность F-мера
$\bf (\gamma =0.5)$
1. Объекты пользователей, которые заходят в 2ГИС реже трёх раз в месяц 0.072 0.349 0.197
2. Объекты пользователей, которые заходят в 2ГИС чаще трёх раз в месяц 0.162 0.457 0.335
3. Объекты пользователей, которые заходят в 2ГИС чаще десяти раз в месяц 0.194 0.514 0.386
Итого по 2-му алгоритму 0.177 0.492 0.363
Итого по 1-му алгоритму 0.153 0.401 0.303

F-мера увеличилась для всех кластеров, кроме первого — ему соответствует самая неактивная часть аудитории и на неё приходится не так много объектов.


Количество истинно-положительных объектов увеличилось на 17%. Прирост в точности составил 9.1%, а в полноте — 2.4%. Общая F-мера увеличилась на 6%.


Если исключить объекты с слишком маленьким количеством уникальных дней, то при тех же параметрах модели полнота вырастает с 0.177 до 0.802 (для первой модели 0.684, то есть прирост на 11.8%) при той же точности в 0.492 (для первой модели 0.401, то есть прирост на 9.1%). И если исходя из этого оценить F-меру $(\gamma =0.5)$, то для второго алгоритма она будет 0.533, а для первого 0.437, то есть прирост составляет 9.6%.


Итог эксперимента на бою


Декомпозиция данных и ввод дополнительных параметров значительно улучшили качество модели. Значит, более сложные модели могут повысить качество результата. Но прежде чем улучшать алгоритм, решили проверить фичу на бою и посмотреть, понравится ли она пользователям.


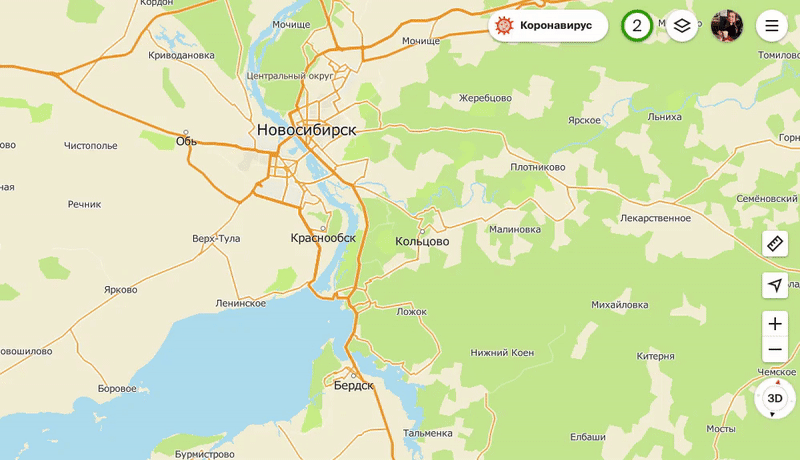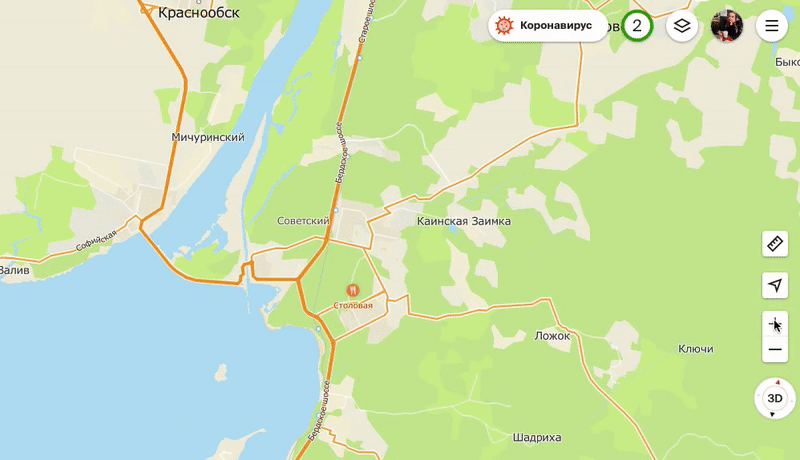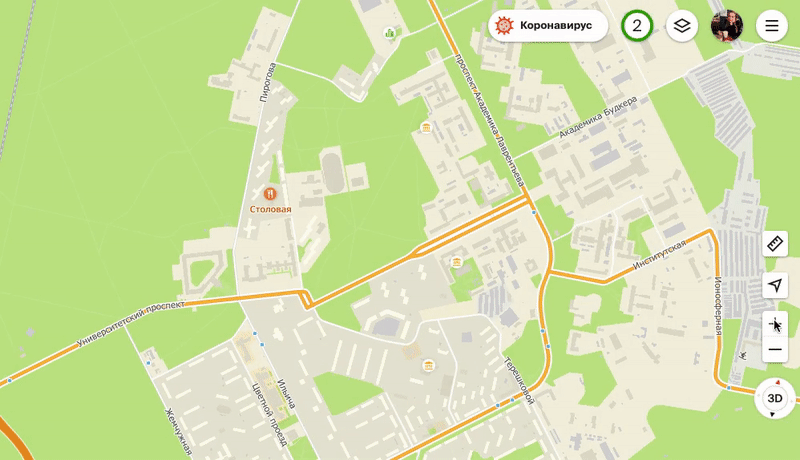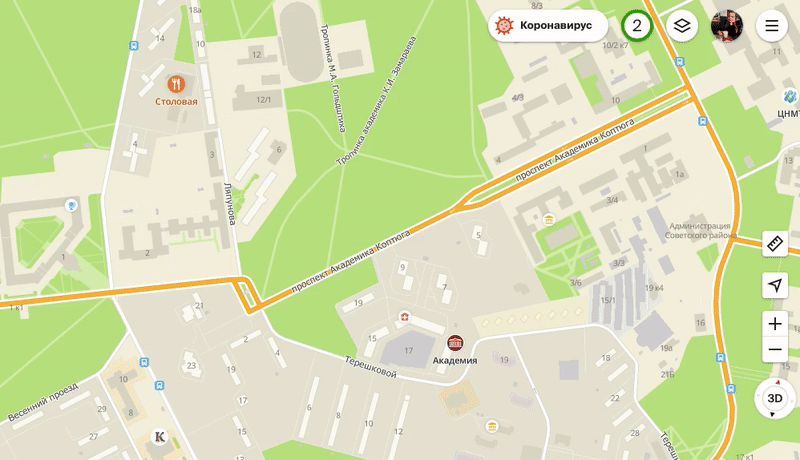
Персонализированные POI чуть больше обычных и появляются на карте раньше них
Персонализированные POI чуть больше обычных и появляются на карте раньше них


За месяц 500 000 пользователей сделали 1 млн кликов по персонализированным POI. Это примерно 12% от тех пользователей, кому мы их подобрали — но это не значит, что остальные пользователи не обратили на них внимание.


Примерно 40% от тех, кому подобрали персонализированные объекты, обращались к этим объектам другими способами. И это тоже хорошо — значит, есть потребность в персонализации не только на карте, но и в других составляющих продукта.


POI vs Избранное


Чтобы оценить, достаточно ли для нас таких результатов, мы решили сравнить персонализированные нами POI с объектами, которые пользователь персонализировал сам — с Избранным.


У персонализированных POI и Избранного похожая цель — запомнить места, в которые хочется вернуться. Похож и внешний вид — они отмечены иконками на карте и имеют примерно один и тот же масштаб отображения. Разница во внешнем виде: значок у всех объектов Избранного всегда один и тот же — белый флажок на оранжевом или красном фоне, а у персонализированных POI цвет и пиктограмма иконки меняется и зависит от отрасли объекта.


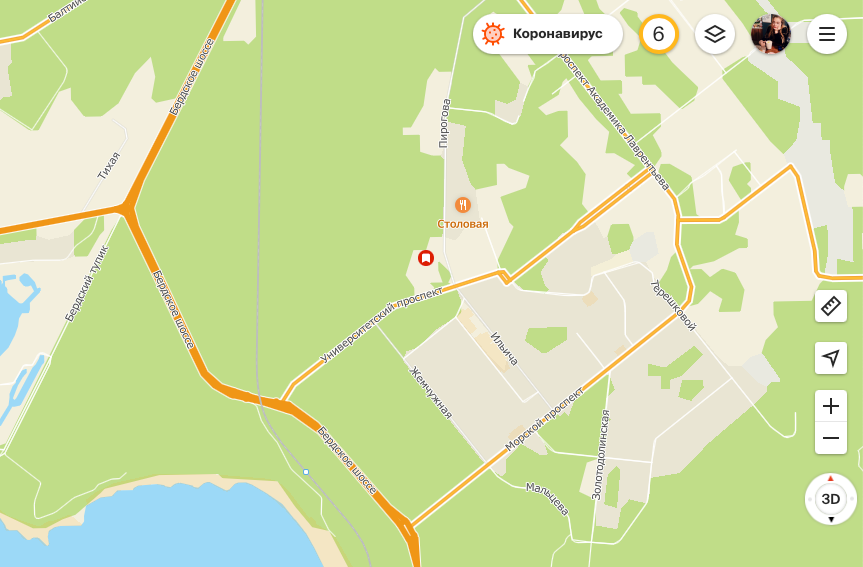
image
Персонализированные POI ещё и подскажут текстом, что за объект нас интересовал — в отличие от иконок Избранного без подписей


Оказалось, что доля пользователей с кликами в персональные POI больше, чем доля пользователей с кликами в Избранное с карты — в два раза среди тех, кому POI вообще были подобраны, и в полтора раза среди всех пользователей.


Фактически, мы сделали для пользователя обновляемое Избранное на карте, за которым ему не надо следить и вообще что-либо самому делать. Это довольно неплохой результат — поэтому есть смысл развивать персональные POI и дальше.


Выводы


Эмпирические модели могут быть полезны и эффективны на начальных этапах запуска фич и в условиях ограниченности ресурсов, потому что они могут дать результат быстро и дёшево. Главное — формировать предположения, исходя из глубокого понимания логики продукта, его природы и поведения пользователей.


Ну и ещё один вывод — будущее за персонализацией.