Изучая курс Алгоритмы на строках столкнулся с задачей о построении суффиксного дерева. Перейдя по ссылке на дополнительные материалы наткнулся на рекомендацию "просмотреть этот замечательный комментарий на Stack Overflow". Изучив и реализовав по приведённому вольному описанию алгоритм Укконена решил поделиться переводом.
Ниже приводится попытка описания алгоритма Укконена; сначала показав, как он работает на простой строке (т.е. строка не содержит повторяющихся символов), постепенно расширяясь до полного алгоритма.
Несколько предварительных утверждений:
То, что мы строим - это в основе похоже на префиксное дерево. Это корневая вершина, чьи ребра выходят из неё в новые вершины, и последующие ребра выходят из них и так далее
Но, в отличие от префиксного дерева, метки ребра - не одиночные символы, у каждого ребра метка это пара чисел [от, до] - указатели на позиции в тексте. В таком случае, каждое ребро содержит строку произвольной длины, но занимает только O(1) памяти (два указателя)
Базовый принцип
Сначала автор хочет продемонстрировать как создать суффиксное дерево чрезвычайно простой строки, строки без повторяющихся символов:
abc
Алгоритм работает по шагам, слева направо. Один шаг на каждый символ строки. Каждый шаг может включать в себя больше чем одну индивидуальную операцию, но мы увидим (смотрите заключительные наблюдения в конце), что общее количество операций O(n).
Мы начинаем слева и сначала вставляем одиночный символ a , создавая ребро из корня к листу и отмечаем его [0, #] - это означает что ребро представляет подстроку начинающуюся с позиции 0 и заканчивающуюся на текущем конце. Автор использует символ # , означающий текущий конец, который указывает на позицию 1 (сразу за a).
У нас есть начальное дерево, которое выглядит так:
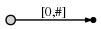
И означает это:

Теперь мы переходим к позиции 2 (сразу за b). Наша цель: на каждом шаге вставлять все суффиксы до текущей позиции. Мы делаем это так:
расширяя существующее
a-ребро доabвставляя новое ребро для
b
В нашем представлении это выглядит так:
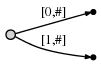
И означает это:
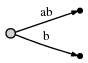
Наблюдается два момента:
Представление ребра для
abтакое же, как и было в начальном дереве:[0, #]. Его значение автоматически изменилось, потому что мы обновили текущую позицию#с 1 на 2.Каждое ребро занимает O(1) места, потому что состоит только из двух указателей на позиции в тексте, независимо от того, сколько символов оно представляет.
Далее мы снова увеличиваем позицию и обновляем дерево добавлением c ко всем существующим ребрам и вставляя одно новое ребро для нового суффикса c.
В нашем представлении:
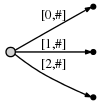
Означает:
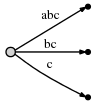
Наблюдения:
Дерево является корректным суффиксным деревом вплоть до текущей позиции после каждого шага
Шагов столько же, сколько и символов в тексте
Объем работы на каждом шаге O(n), потому что все существующие ребра обновляются автоматически приращением
#, а вставка одного нового ребра для конечного символа может выполняться за O(1). Следовательно для строки длинной n, необходимо O(n) времени
Первое расширение: Простое повторение
Конечно, это работает хорошо только потому, что строка не содержит повторений. Сейчас мы рассмотрим более реалистичную строку:
abcabxabcd
Она начинается с abc, как в предыдущем примере, затем ab повторяется с последующим x, а затем повторяется abc с последующим d.
Шаги с 1 по 3: После первых 3 шагов у нас есть дерево из предыдущего примера:
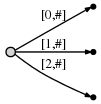
Шаг 4: Сдвигаем # на позицию 4. Это неявно обновляет все существующие ребра:

и нужно вставить конечный суффикс текущего шага a в корень.
Прежде чем сделать это, вводим еще две переменные (в дополнение к #), которые, конечно, существовали всё время, но до сих пор не использовались:
активная точка представляет тройку
(активная_вершина, активное_ребро, активная_длина)остатокпредставляет собой количество новых суффиксов, которые нужно вставить
Точное значение обоих скоро станет ясно, а пока просто скажем:
в простом
abcпримере активная точка всегда была(корень, '\0x', 0), т.е.активная_вершинабыла корневой вершиной,активное_ребробыло указано как нулевой символ '0\x', аактивная_длинабыла нулём. Эффект от этого был в том, что новое ребро, которое добавлялось на каждом шаге, вставлялось в корневую вершину как свежесозданное ребро. Скоро мы увидим почему необходима тройка для представления этой информацииостатоквсегда устанавливался равным 1 на начале каждого шага. Смысл этого был в том, что количество суффиксов, которые необходимо вставить в конце каждого шага, было 1 (всегда только конечный символ)
Теперь это изменится. При вставке текущего конечного символа a в корень замечаем, что уже существует выходящее ребро начинающееся с a, а именно: abca. Вот что мы делаем в таком случае:
Не вставляем свежее ребро
[3, #]в корневую вершину. Вместо этого мы просто замечаем, что суффиксaуже в дереве. Он заканчивается в середине более длинного ребра, но мы не беспокоимся из-за этого. Просто оставляем всё, как есть.Устанавливаем активную точку как
(корень, 'a', 1). Это означает, что активная точка сейчас где-то в середине исходящего из корневой вершины ребра начинающегося сa, а именно, после позиции 1 этого ребра. Наблюдаем, что ребро указано просто его первым символомa. Этого достаточно, потому что может быть только одно ребро начинающееся с конкретного символа (вы убедитесь, что это правда, после прочтения всего описания).Так же приращиваем
остаток, чтобы на начале следующего шага он был равен 2
Spoiler
В оригинале не вставляется ребро [4, #], но очевидно, что a находится на 3 позиции в строке
Наблюдение: Когда конечный суффикс, который нужно вставить, найден уже существующим в дереве, само дерево не изменяется вообще (только обновляется активная точка и остаток). После этого дерево больше не является точным представлением суффиксного дерева вплоть до текущей позиции, но оно содержит все суффиксы (потому что финальный суффикс a содержится неявно). Следовательно, помимо обновления переменных (которые все фиксированного размера, так что это O(1)), более никакой работы не было сделано на текущем шаге.
Шаг 5: обновляем текущую позицию # до 5. Это автоматически обновляет дерево до:
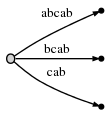
и потому, как остаток равен 2, необходимо вставить два конечных суффикса текущей позиции: ab и b. По существу это из-за того, что:
aсуффикс из предыдущего шага никогда не был вставлен должным образом. Он остался, и поскольку мы продвинулись на один шаг, он вырос садоab.и необходимо вставить новое финальное ребро
b.
На практике это означает, что мы переходим к активной точке (которая указывает за a, что сейчас является ребром abcab), и вставляем текущий конечный символ b. Но: оказывается, что b уже присутствует на этом же ребре.
Итак, мы не меняем дерево. Мы просто:
Обновляем активную точку
(корень, 'a', 2)(та же вершина и ребро, что и раньше, но теперь мы указываем заb)Приращиваем
остатокдо 3, потому что конечное ребро из предыдущего шага всё ещё не вставлено должным образом, и также не вставлено текущее конечное ребро.
Чтобы было ясно: нужно было вставить ab и b на текущем шаге, но поскольку ab уже был найден, мы обновили активную точку и даже не пытались вставить b. Почему? Потому что, если ab находится в дереве, каждый его суффикс (включая b) также должен быть в дереве. Возможно, только неявно, но он должно быть там, из-за метода, которым до сих пор строилось дерево.
Переходим к шагу 6, приращивая #. Дерево автоматически обновляется до:
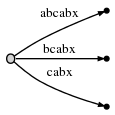
Поскольку остаток равен 3, необходимо вставить abx, bx и x. Активная точка показывает, где заканчивается ab, поэтому нужно только перепрыгнуть туда и вставить x. Действительно, x еще не там, поэтому разделяем ребро abcabx и вставляем внутреннюю вершину:

Представления ребер по-прежнему являются указателями на позиции в тексте, поэтому разделение и вставка внутренней вершины может быть выполнено за время O(1).
Итак, мы разобрались с abx и уменьшили остаток до 2. Теперь нужно вставить следующий оставшийся суффикс bx. Но прежде чем сделать это, необходимо обновить активную точку. Правило для этого, после разделения и вставки ребра, будет называться Правилом 1, и оно применяется всякий раз, когда активная_вершина является корневой (изучим Правило 3 для других случаев ниже).
Правило 1, после вставки из корня:
-
активная_вершинаостается корнем-
активное_ребростановится первым символом нового суффикса, который нужно вставить, т.е.b-
активная_длинауменьшается на 1
Cледовательно, новая тройка активной точки (корень, 'b', 1) указывает, что следующая вставка должна быть сделана на bcabx ребре, за 1 символом, то есть за b. Можно идентифицировать точку вставки за время O(1) и проверить, присутствует ли уже x или нет. Если бы он присутствовал, текущий шаг закончился и все бы осталось как есть. Но x нет, поэтому мы вставляем его, разделяя ребро:
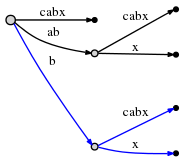
Это заняло время O(1), и остаток обновляется до 1, а активная точка до (корень, 'x', 0), как указано в правиле 1.
Но нужно сделать еще кое-что. Назовем это Правилом 2:
Если ребро разделяется
ивставляется новая вершина, и если это не первая вершина, созданная на текущем шаге, ранее вставленная вершина и новая вершина соединяются через специальный указатель, суффиксную ссылку.
Spoiler
1 дополнение к правилу 2
Если вставляется новая вершина, и если это не первая вершина, созданная на текущем шаге, ранее вставленная вершина и активная вершина соединяются через специальный указатель, суффиксную ссылку.
Позже мы увидим, почему это полезно. Вот что мы получаем (суффиксная ссылка представлена пунктирным ребром):

Всё ещё нужно вставить конечный суффикс текущего шага, x. Поскольку компонент активная_длина активной вершины снизился до 0, конечная вставка выполняется непосредственно в корень. Поскольку в корневой вершине нет исходящего ребра начинающегося с x, вставляем новое ребро:
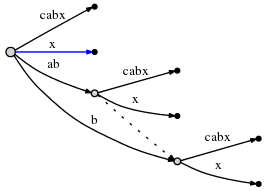
Spoiler
Применяем правило 2, так как существует ранее созданная вершина
Как видно, на текущем этапе все оставшиеся вставки были сделаны.
Переходим к шагу 7, устанавливая # = 7, что, как всегда, автоматически добавляет следующий символ a ко всем листовым ребрам. Затем пытаемся вставить новый конечный символ в активную точку (корень) и обнаруживается, что он уже там. Текущий шаг завершается, ничего не вставляется, но обновляется активная точка до (корень, 'a', 1).
Spoiler
под листовыми ребрами подразумеваются ребра оканчивающиеся на #
на практике указатели хранятся в вершинах, а не в ребрах, поэтому приращивание # автоматически обновляет все листовые вершины
На шаге 8, # = 8, добавляется b, и, как было показано ранее, это только означает, что обновляется активная точка до (корень, 'a', 2) и увеличивается остаток, не делается ничего другого, потому что b уже присутствует. Однако наблюдаем (за время O(1)), что активная точка теперь находится в конце ребра. Это отражается в её переустановлении на (вершина1, '\0x', 0). Здесь автор использует вершина1 для обозначения внутренней вершины, на которой заканчивается ребро ab.
Далее, на шаге # = 9 нужно вставить 'c', и это поможет нам понять последний трюк:
Второе расширение: Использование суффиксных ссылок
Как всегда, обновление # автоматически добавляет c к листовым ребрам, и мы переходим к активной точке, чтобы посмотреть, можно ли вставить 'c'. Оказывается, 'c' уже существует на этом ребре, поэтому активная точка устанавливается как (вершина1, 'c', 1), увеличивается остаток и больше ничего не происходит.
Теперь на шаге # = 10 остаток равен 4, и поэтому сначала нужно вставить abcd (который остался с 3 шагов назад), вставив d в активную точку.
Попытка вставить d в активную точку способствует разделению ребра за время O(1):

активная_вершина, из которой было инициировано разделение, отмечена красным выше. Вот последнее правило
Правило 3
После разделения ребра из
активная_вершина, которая не является корнем, переходим по суффиксной ссылке, выходящей из этой вершины, если таковая имеетсяактивная_вершинаустанавливается вершиной, на которую она указывает. Если суффиксная ссылка отсутствует,активная_вершинаустанавливается корнем.активное_реброиактивная_длинаостаются без изменений.
Активная точка теперь (вершина2, 'c', 1), а вершина2 отмечена красным ниже:
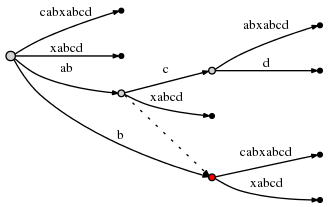
Поскольку вставка abcd завершена, остаток уменьшается до 3 и рассматривается следующий оставшийся суффикс текущего шага: bcd. Правило 3 установило активную точку как раз на нужную вершину и ребро, поэтому вставку bcd можно выполнить, просто вставив ее конечный символ d в активную точку.
Это вызывает еще одно разделение ребер, а из-за правила 2 необходимо создать суффиксную ссылку от ранее вставленной вершины к новой:
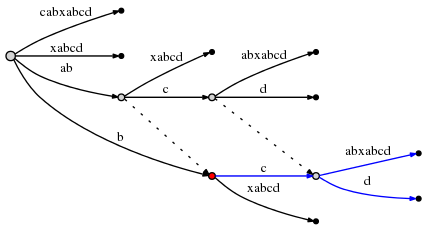
Наблюдение: суффиксные ссылки позволяют переназначить активную точку, чтобы можно было сделать следующую остающуюся вставку за O(1). Посмотрите на граф выше, чтобы убедиться, что на самом деле вершина на метке ab связана с вершиной с меткой b (её суффикс), а вершина с abc связана с bc.
Текущий шаг еще не закончен. остаток теперь равен 2, и нужно следовать правилу 3, чтобы снова переназначить активную точку. Поскольку текущая активная_вершина (красная выше) не имеет суффиксной ссылки, она становится корнем. Теперь активная точка (корень, 'c', 1).
Следовательно, следующая вставка происходит на одном исходящем ребре корневой вершины, чья метка начинается с c: cabxabcd, после первого символа, то есть после c. Это вызывает еще одно разделение:
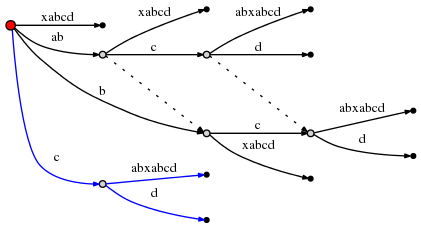
И поскольку это включает в себя создание новой внутренней вершины, следуем правилу 2 и устанавливаем новую суффиксную ссылку из ранее созданной внутренней вершины:
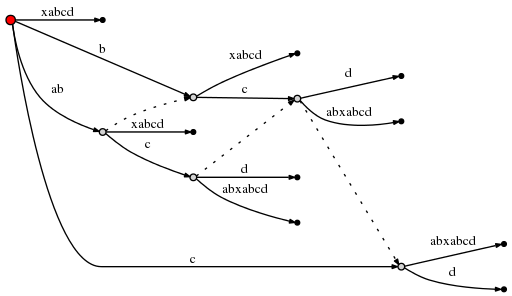
(автор использует Graphviz Dot для этих маленьких графов. Новая суффиксная ссылка заставила переупорядочить существующие ребра, поэтому внимательно проверьте, чтобы убедиться, что единственное, что было вставлено выше - это новая суффиксная ссылка)
При этом остаток может быть установлен равным 1, и поскольку активная_вершина является корневой, то используется правило 1 для обновления активной точки до (root, 'd', 0). Это означает, что последней вставкой текущего шага является вставка единственного d в корень:
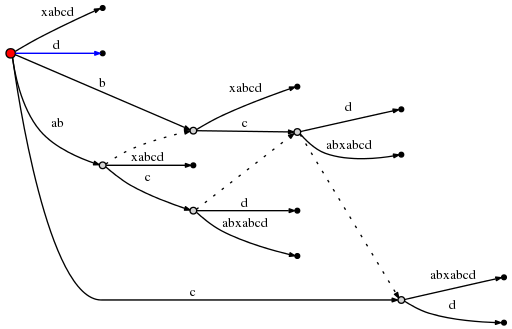
Spoiler
Применяем правило 2
Это был последний шаг, и мы закончили. Однако есть ряд заключительных замечаний:
На каждом шаге # перемещается вперед на 1 позицию. Это автоматически обновляет все листовые вершины за O(1).
Но это не касается:
любых суффиксов, оставшихся от предыдущих шагов
одного последнего символа текущего шага.
остаток отображает, сколько дополнительных вставок нужно сделать. Эти вставки индивидуально соответствуют конечным суффиксам строки, которая заканчивается в текущей позиции #. Рассматриваем суффиксы один за другим и делаем вставку. Важно: каждая вставка выполняется за O(1), так как активная точка сообщает, куда именно идти, и нужно добавить только один единственный символ в активную точку. Почему? Потому что другие символы неявно содержатся (иначе активной точки не было бы там, где она есть).
После каждой такой вставки остаток уменьшается и происходит переход по суффиксной ссылке, если она есть. Если нет, то переход в корень (правило 3). Если уже в корне, то модифицируется активная точка, используя правило 1. В любом случае это занимает всего O(1) времени.
Если во время одной из этих вставок обнаруживается, что символ, который хочется вставить, уже существует, ничего не делается и текущий шаг завершается, даже если остаток> 0. Причина в том, что все оставшиеся вставки будут суффиксами той, которую только что пытались сделать. Следовательно, все они неявны в текущем дереве. Тот факт, что остаток> 0, гарантирует, что с остальными суффиксами разберутся позже.
Spoiler
2 дополнение к правилу 2
Если текущий шаг завершается при остаток>0, и если это не первая вершина, созданная на текущем шаге, ранее вставленная вершина и активная вершина соединяются через специальный указатель, суффиксную ссылку.
Что, если в конце алгоритма остаток> 0? Так будет всегда, когда конец текста - это подстрока, которая встречалась где-то раньше. В этом случае нужно добавить один дополнительный символ в конец строки, которого раньше не было. Обычно для этого обычно используется знак доллара $. Почему это имеет значение? > Если позже законченное дерево суффиксов будет использовано для поиска суффиксов, совпадения должны приниматься, только если они заканчиваются в листе. В противном случае получится много ложных совпадений, потому что в дереве неявно содержится много строк, которые не являются фактическими суффиксами основной строки. Принуждение остаток к нулю в конце - это, по сути, способ гарантировать, что все суффиксы заканчиваются на листовой вершине. Однако, если дерево используется для поиска общих подстрок, а не только суффиксов основной строки, этот последний шаг на самом деле не требуется.
Какова сложность всего алгоритма? Если длина текста n символов, очевидно, что есть n шагов (или n + 1, если добавляется знак доллара). На каждом шаге либо ничего не делается (кроме обновления переменных), либо происходит количество вставок равных остаток, каждая из которых занимает O(1) времени. Поскольку остаток указывает, сколько раз ничего не делалось на предыдущих шагах, и уменьшается для каждой вставки, которая делается сейчас, общее количество раз, которое делается что-то, равно ровно n (или n + 1). Следовательно, общая сложность O(n).
Однако есть одна мелочь, которую автор не объяснил должным образом: может случиться так, что перейдя по суффиксной ссылке, обновив активную точку, а затем обнаружим, что ее компонент активная_длина плохо соотносится с активная_вершина. Например, рассмотрим такую ситуацию:
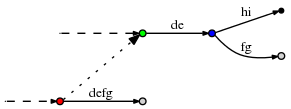
(Пунктирными линиями обозначена остальная часть дерева. Точечная линия обозначает суффиксную ссылку)
Теперь представьте, что активная точка равна (красная, 'd', 3), чтобы она указывала на позицию за f на краю defg. Теперь предположим, что мы сделали необходимые обновления и теперь переходим по суффиксной ссылке, чтобы обновить активную точку в соответствии с правилом 3. Новая активная точка (зеленая, 'd', 3). Однако d-ребро, выходящее из зеленой вершины - это de, поэтому в нем всего 2 символа. Чтобы найти правильную активную точку, нам, очевидно, нужно пройти по этому ребру к синей вершине и обновить его до (синяя, 'f', 1).
В особенно плохом случае активная_длина может быть такой же большой, как и остаток, который может достигать n. И вполне может случиться так, что для нахождения правильной активной точки нам нужно перепрыгнуть не только через одну внутреннюю вершину, но, возможно, через многие, вплоть до n в худшем случае. Означает ли это, что алгоритм имеет скрытую сложность O(n2), потому что на каждом шаге остаток обычно O(n), а пост-корректировки активная_вершина после перехода по суффиксной ссылке тоже могут быть O(n)?
Нет. Причина в том, что если нам действительно нужно настроить активную точку (например, с зеленой на синюю, как указано выше), это приведет нас к новой вершине, которая имеет свою собственную суффиксную ссылку, и активная_длина будет уменьшена. По мере того, как мы переходим по цепочке суффиксных ссылок, мы делаем оставшиеся вставки, активная_длина может только уменьшаться, а количество корректировок активных точек, которые мы можем сделать в пути, не может быть больше, чем активная_длина в любой момент времени. Поскольку активная_длина никогда не может быть больше, чем остаток, а остаток равен O(n) не только на каждом отдельном шаге, но и общая сумма приращений, когда-либо сделанных для остаток в ходе всего процесса тоже O(n), то количество корректировок активной точки также ограничена O(n).
Примечания переводчика
В целом алгоритм описан легким и понятным языком. Следуя описанию, возможно его реализовать, а естественные оптимизации произойдут на лету. Те места, которые создали мне сложности, выделил спойлерами.
В моей реализации используется алфавит ACGT, так как преследовал цель прохождения тестов для задачи внутри курса.

