Если хочется сделать передачу или хранение данных более надёжными, применив к ним избыточное кодирование, то для этого неплохо подойдёт код Рида-Соломона. Понимаю, что на эту тему написано немало материала, тем не менее ориентирован он, как правило, на людей неплохо подготовленных в математике. Если просто хочется реализовать такой алгоритм в каком-нибудь проекте, не сильно углубляясь в математику, то надеюсь этот материал будет весьма полезным.
При кодировании Рида-Соломона сообщения представляются в виде полиномов, дальше с этими полиномами выполняются разные арифметические операции. Но прежде чем приступать к операциям над полиномами нужно вспомнить (узнать) об полях Галуа.
Арифметика в поле Галуа GF[256]
В своей предыдущей, первой во всех смыслах статье, я подробно описал, как можно реализовать умножение в полях Галуа и приводил пример кода на C#. Там же я кратко писал что такое поля Галуа и зачем они нужны.
Напомню. В нашей привычной арифметике результатом операции деления может оказаться дробное число вроде (1/3). В десятичном представлении это 0,3333333… и так далее. Такие числа не очень удобны для компьютерных вычислений, так что для кодирования информации решили применить давно придуманные поля Галуа. Здесь числа это такие же привычные нам числа, только их количество – это строго определённая величина. Для кодирования хорошо подходит поле GF[256] (Galois Field 256 – поле Галуа, содержащее 256 элементов), То есть вместо всех привычных значений от до , с вообще всеми возможными промежуточными, включая , , 42, а также гугол и прочие, у нас есть 256 чисел: 0, 1, 2… 255. Всё. Никаких тебе 7092, 3,15 и 2/3. Только числа из списка. (42 — в списке. Без паники).
Но просто так числа ничего не дают. Вся их польза – это операции. Их можно складывать, вычитать, делить и умножать, только это не просто так сложил-вычел. Результат сложения-вычитания-деления-умножения есть число также от 0 до 255. Какое это число? Два плюс два равно сколько? Так вот, ни разу не 4. 2+2=0. Вообще, сложение в GF[256] работает также, как и вычитание. это побитовое исключающее «или» – XOR. Умножение-деление — там другие правила, но на простейшем уровне можно считать, что это таблицы. Так как чисел ограниченное количество, то можно составить всеобъемлющую таблицу умножения. Каким образом? Совсем детально здесь не буду распространяться. Про умножение – подробно писал в предыдущей статье, деление и возведение в степень проще всего реализовать используя таблицы степеней и логарифмов. Да, умножение тоже можно реализовать с помощью логарифмов, так эта операция выполняется быстрее.
Ну конечно же, кодирование и декодирование будут делать не специально обученные эмигранты с калькуляторами. Это должно быть реализовано программно. Конечно же это должен быть язык низкого уровня, какой кому ближе. Может быть, даже verilog (в этом случае речь идёт уже об аппаратной реализации, и на самом деле, как заметили в комментариях, verilog относится к языкам высокого уровня). Для того чтобы разобраться как работает кодирование, для себя я решил написать все алгоритмы на высокоуровневом C#, но постарался не сильно задействовать высокий уровень абстракции. Просто чтобы разобраться. Должен сразу сказать, что мой код ни коим образом не претендует ни на быстродействие, ни на оптимальность или на правильность с точки зрения ООП либо каких-нибудь ещё паттернов или подходов. Единственно, я старался, чтобы код был максимально понятным. Весь код вместе с каким-никаким GUI выложен на гитхабе. Собирается под win в VS2019. Бинарник тоже выложен.
Для начала нужно составить таблицы степеней и логарифмов примитивного члена. Здесь надо напомнить (рассказать) про свойство возведения в степень в поле Галуа. Если последовательно умножать (по правилам поля, конечно) двойку: , то начиная со степени 255 результат начнёт повторяться, то есть и также . Если упорно продолжить умножать дальше, пока есть терпение и деньги на зарплату эмигрантам, то результат будет такой:
и так далее. Значения, если использовать порождающий полином 285 (о нём было в предыдущей статье сейчас это не сильно важно), такие: Также в промежутке от до включительно нет ни одного повторяющегося результата. А это значит, что любое число (кроме нуля) из поля GF[256] можно записать как два в какой-нибудь степени. И что из этого? А вот что. Правила умножения и деления степеней здесь выполняются. То естьа также . Это вместе значит, что не надо заморачиваться и реализовывать алгоритмы умножения и деления по сложным правилам, достаточно лишь узнать в какой степени двойка для каждого множителя (логарифм) и сложить или вычесть степени чтобы произвести операции умножения или деления. Пример: Возведение в степень и нахождение логарифма – просто обращение к массивам, в которых по 256 элементов (так как , для таблицы степеней достаточно 255 элементов).
Теперь нужно сделать пару важных оговорок для тех, кто захочет самостоятельно реализовать алгоритмы исходя из описания. (Когда я изучал вопрос, везде эти вещи считались «очевидными» со всеми вытекающими)
- Во-первых: В примере выше мы возводили в степень число 2. Для числа 2 выполняется правило об уникальности степеней от 0 до 254. Не для каждого числа поля это верно. Те числа, для которых это верно – это примитивные члены поля. Часто в литературе обозначают как . При кодировании Рида-Соломона число неоднократно вспоминают и используют. Хотя его выбор не влияет на арифметику, результат кодирования будет отличаться в зависимости от выбора.
- Во-вторых: Когда мы говорим о сложении и вычитании степеней при умножении и делении, то речь идёт не о сложении и вычитании по правилам поля Галуа. Здесь это просто сложение и вычитание. Могут получиться как отрицательные значения, так и числа больше 255 результат при этом легко найти, помня о том, что степени повторяются через каждые 255 значений, то есть, например, степень 257 равна степени 2, а степень -1 равна степени 254.
Теперь имея описание умножения-деления-сложения-вычитания можно составить алгоритм на каком нравится языке. Для составления таблицы степеней и логарифмов можно взять функцию умножения из предыдущей статьи. В коде ниже есть ещё операция инвертирования, это 1/x и возведения числа в степень. Для кодирования Рида-Соломона можно обойтись и без них, но можно и воспользоваться. Они также используют свойства степени: Умножение здесь не по правилам поля Галуа, а обычное привычное нам.
public static void MakePowTable(uint New_GF_Byte_poly, uint New_GF_Byte_prim_memb, bool ShowMessageboxes) {
//Если есть функция умножения, то составить таблицу степеней и логарифмов
//не составляет никакого труда, ведь возведение в степень – есть умножение
//несколько раз подряд
//Здесь создаётся таблица степеней методом последовательного умножения
//примитивного члена (как правило выбирают число 2, но здесь это может
//быть любое число).
//Затем таблица проверяется на наличие повторяющихся значений. Если нет
//повторяющихся значений, то выбранный примитивный член и порождающий
//полином сохраняются вместе с вычисленными таблицами.
//для параметра New_GF_Byte_prim_memb валидны следующие значения:
//285, 299, 301, 333, 351, 355, 357, 361, 369, 391, 397, 425, 251, 463,
//487, 501.
//Этот массив можно сделать на единицу меньше, так как для поля GF[256]
//верно, что a^0= ^255, но чтобы не путаться оставляю 256 элементов массива.
byte[] tmp_GF_256_power_a = new byte[256];
byte[] tmp_GF_256_log_a = new byte[256];
GF_256_power_a = new byte[256];
GF_256_log_a = new byte[256];
uint tmp_GF_Byte_poly = New_GF_Byte_poly;
uint tmp_GF_Byte_prim_memb = New_GF_Byte_prim_memb;
//Пропишем тривиальные вещи как то: a^0=1 и a^1=a, и наоборот
tmp_GF_256_power_a[0] = 1;
tmp_GF_256_log_a[1] = 0;
tmp_GF_256_power_a[1] = (byte)tmp_GF_Byte_prim_memb;
tmp_GF_256_log_a[tmp_GF_Byte_prim_memb] = 1;
//Остальные члены поля
for (int i = 2; i < 256; i++) {
tmp_GF_256_power_a[i] = (byte)GF_b2_Aryth.Galois_b2_ext_mult(tmp_GF_Byte_prim_memb, tmp_GF_256_power_a[i - 1], tmp_GF_Byte_poly);
//Для значения степени "0" тут проходят 2 значения: 1 и 255. Это надо учесть
if(0 != tmp_GF_256_power_a[i]) {
tmp_GF_256_log_a[tmp_GF_256_power_a[i]] = (byte)i;
}
}
bool Ok = true;
//Для поля GF[256] верно, что a^0 = a^255. Так что проверка
//не затрагивает степень 255
for (int i = 0; i <= 254; i++) {
for (int j = 0; j <= 254; j++) {
if (i != j) {
if (tmp_GF_256_power_a[i] == tmp_GF_256_power_a[j]) {
Ok = false;
}
}
}
}
//Копируем в используемые таблицы, если нет повторов в таблице
//степеней выбранного примитивного члена
if (Ok) {
for (int i = 0; i < 256; i++) {
GF_256_power_a[i] = tmp_GF_256_power_a[i];
}
for (int i = 0; i < 256; i++) {
GF_256_log_a[i] = tmp_GF_256_log_a[i];
}
GF_256_poly = tmp_GF_Byte_poly;
GF_256_prim_memb = tmp_GF_Byte_prim_memb;
if (ShowMessageboxes) { MessageBox.Show("Всё хорошо. При таком сочетании порождающего полинома и примитивного члена в таблице степеней примитивного члена (a^1 .. a^255) нет повторений."); }
} else {
if (ShowMessageboxes) { MessageBox.Show("Всё плохо! При таком сочетании порождающего полинома и примитивного члена в таблице степеней примитивного члена есть повторяющиеся значения."); }
}
}
public static byte Pow_a(int Degr) {
//Возведение примитивного члена в степень. Свойство степени в поле
//Галуа GF[256] таково, что степень примитивного члена 0 равна
//степени 255; 1 - 256; 2 - 527 и так далее.
if (0 <= Degr && Degr < 255) {
return GF_256_power_a[Degr];
} else {
int TmpDegr = Glob.IntMod(Degr);
TmpDegr %= 255;
//Хоть и не существует отрицательных чисел в поле Галуа, здесь под
//отрицательной степенью подразумевается число обратное.
if (Degr < 0) {
TmpDegr = 255 - TmpDegr;
}
return GF_256_power_a[TmpDegr];
}
}
public static byte Log_a(byte Arg) {
//Логарифм по основанию примитивного члена
if (0 == Arg) {
throw new Exception("Argument cannot be zero in GF_Byte.Log_a(Arg)");
//Логарифм единицы в GF[256] равен нулю и 255, так как a^0==a^255.
//Для кодирования Рида-Соломона выбираем 0.
} else if (1 == Arg) {
return 0;
}else {
return GF_256_log_a[Arg];
}
}
public static byte Inverse(byte Arg) {
//Можно обойтись и без этой функции и писать Div(1, Arg)
if (1 == Arg) { return 1; }
return GF_256_power_a[255 - GF_256_log_a[Arg]];
}
public static byte Add(byte a1, byte a2) {
//Сложение таково же как и вычитание - побитовое "ИЛИ"
return (byte)(a1 ^ a2);
}
public static byte Sub(byte s1, byte s2) {
//Вычитание таково же как и сложение - побитовое "ИЛИ"
return (byte)(s1 ^ s2);
}
public static byte Mult(byte m1, byte m2) {
//Умножение с использованием таблиц степеней и логарифмов.
//Довольно таки быстрая операция
if (0 == m1 || 0 == m2) { return 0; }
return Pow_a(Log_a(m1) + Log_a(m2));
}
public static byte Div(byte d1, byte d2) {
//Деление с использованием таблиц степеней и логарифмов.
if (0 == d2) { throw new Exception("Division by zero"); }
if (0 == d1) { return 0; }
return Pow_a(Log_a(d1) - Log_a(d2));
}
public static byte Pow(byte b, int p) {
//Возведение в степень с помощью таблиц логарифмов и степеней.
//Так как нуль в степени нуль равно одному, сначала проверяем
//на равенство нулю показателя
if (0 == p) { return 1; }
if (0 == b) { return 0; }
byte BaseLog = GF_256_log_a[b];
int TmpDegr = Glob.IntMod(p);
TmpDegr = TmpDegr * BaseLog;
TmpDegr %= 255;
if (p < 0) {
TmpDegr = 255 - TmpDegr;
}
return GF_256_power_a[(byte)TmpDegr];
}
И так, мы построили свою арифметику. С целыми числами и делением без остатка. Для простоты использования чисел GF[256] можно создать класс и в нём переопределить операции сложения, вычитания, деления и умножения. Так дальнейший код будет немного короче.
Полиномы
Переходим к полиномам. Для кодирования Рида-Соломона сообщения представляются в виде полиномов. Как правило, считается, что этой фразы достаточно. Но я распишу поподробнее, потому что, когда я изучал вопрос мне было не до конца всё понятно. Полином – это выражение вроде такого:
Член полинома – это или . Степень члена – это показатель , коэффициент члена это множитель перед x. Теперь, если мы хотим представить сообщение в виде полинома, то числовые значения байт сообщения мы записываем как коэффициенты членов. Ещё одна оговорка: при реализации умножения в поле Галуа (без таблиц степеней и логарифмов) также используются полиномы. Эти полиномы не имеют никакого отношения к тем, что мы рассматриваем здесь. Как говорится: «Это другое!»
Например нам нужно закодировать сообщение «DON'T PANIC». Для этого нужно перевести символы в числа. С русскими буквами было бы сложнее, там на каждый символ (UTF8) приходится по 2 байта. А здесь воспользуемся UTF8, или ASCII и получим: 44 4F 4E 27 54 20 50 41 4E 49 43 – это в шестнадцатеричном виде, или 68, 79, 78, 39, 84, 32, 80, 65, 78, 73, 67 обычными числами. Теперь записываем каждое число как коэффициент перед x, и получаем, что сообщению «DON'T PANIC» соответствует такой полином:
Степени можно расположить как в порядке возрастания, так и в порядке убывания. Полином в зависимости от этого остаётся полиномом, но становится другим полиномом и об этом надо помнить. То есть, выбор порядка нужно сделать один раз и его придерживаться. (В зависимости от этого выбора избыточные символы при кодировании будут находиться в начале или в конце сообщения). Для себя я выбрал возрастание степеней. Полином при этом выглядит задом наперёд (нулевая степень в начале, а не в конце, как принято в математике), но при этом номер члена равен его степени. Избыточные символы при кодировании будут в начале. При написании кода можно хранить лишь массив с коэффициентами, так что кодируемое сообщение это просто массив байт.
Операции с полиномами
Сложение и умножение полиномов (многочленов) – это, на самом деле, восьмой класс средней школы (точно не помню, может другой). Кому-то покажется излишним (мне точно кажется), но для полноты картины распишу с примерами. Для кодирования я выбрал записывать полиномы в порядке убывания степеней членов, так что и в примерах буду записывать также. Закодированное сообщение из примера выше в виде полинома довольно-таки громоздко, поэтому для примеров будут просто рандомные полиномы невысоких степеней.
Сложение полиномов
Для того чтобы сложить два полинома мы просто складываем коэффициенты при одинаковых степенях по правилам поля Галуа. Всё. Пример: выполняем следующую операцию:
Для программной реализации (и для кодирования) лучше записать полиномы так, чтобы они были одной длины и с явным указанием степеней:
В результате имеем:
Так как в поле GF[256] вычитание эквивалентно сложению то пишу только знак "+". Вычитание полиномов также эквивалентно сложению полиномов.
Умножение полиномов
При умножении каждый член одного полинома умножается на каждый член второго. Результат складывается:
Когда мы перемножаем и складываем коэффициенты — мы используем правила умножения и сложения поля Галуа GF[256]. Сложение степеней — это обычное сложение, то есть:
Деление полиномов
С делением всё немного сложнее, но тоже ничего сверхъестественного. Это как деление столбиком, только с полиномами. Берём старший член делимого и старший делителя. Делим, записываем результат. Полученное умножаем на делитель и вычитаем (прибавляем – в поле Галуа неважно) из делимого. Далее результат вычитания делим также, как делили изначально. Всё повторяется до тех пор, пока старшая степень остатка больше или равна старшей степени делителя.
Пример:
Нужно разделить на . Записываем в столбик. Затем делим старшие члены: на (деление по правилам поля Галуа, вычитание степени — обычное). Результат записываем.

Теперь умножаем на . Получаем записываем это под делимым и складываем. Результат сложения также записываем под чертой (это остаток)
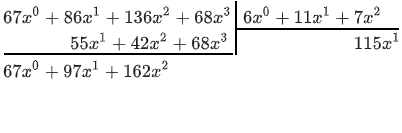
Теперь остаток также делим на делитель. (Делим старшие члены) умножаем — вычитаем — всё как на первом шаге:

В остатке теперь старший член – это . Степень меньше, чем у старшего члена делителя () – значит всё, деление закончено. Частное это , остаток .
Код деления умножения и вычитания хоть и не очень сложный, но довольно-таки громоздкий вместе со всеми вспомогательными функциями, без которых код не очень понятен. Думаю, здесь его приводить нет особого смысла. Но всё же продублирую ссылку на Github: https://github.com/AV-86/Reed-Solomon-Demo/releases
И какой толк от всех этих ваших полиномов? В принципе без алгоритмов кодирования-декодирования Рида-Соломона я не знаю как их с пользой применить. Слышал краем уха, что они также применяются при шифровании информации. Непосредственно как кодировать и декодировать по методу Рида-Соломона напишу в следующей статье, а пока, благодарю за внимание!


livsius
Только verilog — это не программа, это описание железа.
av-86 Автор
Безусловно! Verilog это не программа. Verilog — это язык. Тем не менее рисовать схему не надо, надо писать код. Наверное, действительно вопрос спорный, можно ли называть этот код программным. Аргументом в пользу того, что всё-таки можно, может служить, то, что на verilog мы пишем код для синтезатора, и называть его аппаратным не совсем корректно. Разработчики языка старались сделать его похожим на Си, и им это удалось, так что легко попутать. Спасибо за замечание, добавлю уточнение в статью.
livsius
Фраза <verilog — это не программа> подразумевала по смыслу < код на verilog — это не программа>.
Вопрос тут абсолютно не спорный, а однозначный. Важно не то, куда вы скармливаете код, а то, что этот код описывает.
Программный код описывает алгоритм. Код verilog (его синтезируемое подмножество) описывает электрическую схему. И это их ключевое отличие друг от друга.
И разработчики языка, сделав его похожим на СИ, не подразумевали, что это еще один язык программирования, конечно. Просто создан он был под влиянием синтаксиса Си, который был тогда очень распространен. Но, конечно, семантика verilog ничего общего не имеет с семантикой Си.
av-86 Автор
Тогда ещё аргумент. Когда мы применяем распространённую аббревиатуру SDR (software defined radio), то как вы переводите её на русский язык?
livsius
Радио реализованное программно. А что?
Почему вы рассматриваете этот вопрос как аргумент?
av-86 Автор
Потому, что вы сами применили «программно», хотя довольно-таки часто SDR реализуется на ПЛИС. Я это всё не к тому, что код на verilog однозначно «программный», а к тому, что однозначности нет.
livsius
Во-первых, вы делаете странный "логический" вывод: <довольно-таки часто SDR реализуется на ПЛИС> --> < verilog может считаться программой>
Во-вторых, вы не совсем правильно понимаете идею SDR.
На пальцевом уровне идея следующая: сырой, грубо отфильтрованный аналоговый сигнал нормализуется по амплитуде (усиливается но нужного уровня) и преобразуется с помощью АЦП в цифровую форму и посылается в виде сырого потока цифровых данных на порт обычного компьютера. И вся последующая обработка (фильрация, декодирование, тд) выполняется с помощью процессора общего назначения ПРОГРАММНО.
Отсюда и название метода "Software Defined" пошло. ПЛИС могут использовать а могут и не использовать для аппаратного ускорения программных алгоритмов, но не использование ПЛИС дало название подходу. Существует куча реализаций без каких-либо ПЛИС вообще, погуглите те же USB ТВ тюнеры, испрользуемые для SDR.
Существует куча ПЛИС-based аппаратных ускорителей разного рода алгоритмов (те же crypto-coin miner boards). Никто не называет их "software defined miner" или чем-то похожим. В данном случае использование ПЛИС лишь позволяет на коленке сделать железку с нужным функционалом вместо выпуска ASIC кристалла, и никак не переводит железку в категорию "Software defined".
Как ни крути, но все-таки код verilog — это не программа, а лишь еще один формат (помимо графического) описание аппаратной схемы.