По моему глубокому убеждению, все задачи делятся на два типа: простые и сложные. У простых задач есть простые решения (пусть и требующие для их нахождения некоторого объёма специальных знаний), а сложных задач в математике нет. Чтобы проиллюстрировать это, я покажу вам удивительное в своей простоте доказательство вынесенного в заголовок поста утверждения. Одной картинкой.
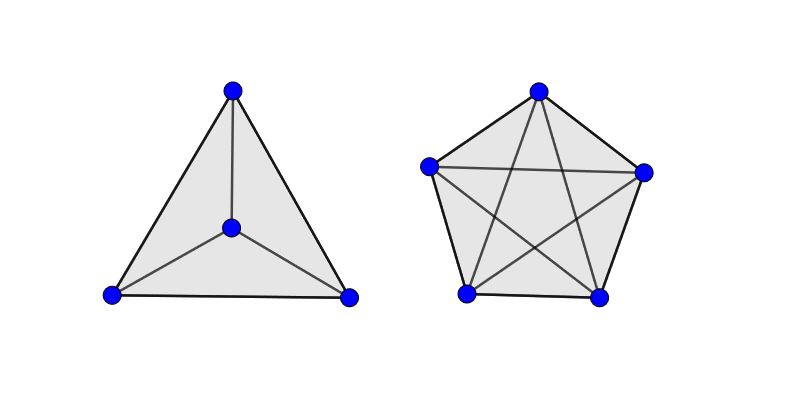
Для начала, что изображено на картинке? Однозначного математического ответа на этот вопрос нет: с геометрической точки зрения это ортогональные проекции пятиячейника на плоскости Коксетера A2 и A4, а с точки зрения теории графов — диаграммы K4 и K5.
Геометрия нагляднее, интуитивнее и потому гораздо проработаннее остальной математики, поэтому своё R(5,5) в ней давно нашли: этой публикацией доказано, что существует ровно 39 компактных арифметических групп треугольников общего вида и 4 паракомпактных группы прямоугольных треугольников, что в сумме даёт искомое 43 — произвольный пятиячейник не может быть однозначно определён меньшим количеством групп, а необходимости в уточнении паракомпактных групп компактными нет. Собственно, на этом доказательство можно считать оконченным, так что дальше я буду лить воду на мельницу теории графов, брюзжать и рассказывать как до всего этого докатился.
С чего всё началось
Всё началось с того, что девушка приняла моё предложение и на горизонте замаячили большие расходы — свадьба штука весьма затратная. Разумеется, на следующий день я начал думать над этим вопросом; ответ нашёлся довольно быстро: в математике есть куча наград с денежными премиями и если решить какую-нибудь сложную задачу, то одну из этих премий почти наверняка дадут. Так как предмет я знаю хорошо, остальное было делом техники.
Числа Рамсея идеально вписались в мой план: задачи их нахождения формулируются просто, интуитивно понятны и при этом сложны настолько, что за последние полвека прогресса в решениях почти нет — словом, игнорировать их было попросту глупо. Чтобы составить общее впечатление о проблеме рекомендую прочитать эти два поста на Хабре и узнать здесь детали. Примерно понятно о чём пойдёт речь? Тогда приступим.
Используемые определения:
(Простой неориентированный) граф — это пара множеств (V, E) (множество вершин и множество рёбер), причём E ? {{v1, v2} | v1, v2 ? V, v ? v2}.
Диаграмма графа — наглядное изображение графа, на котором вершины графа изображаются точками, а рёбра — линиями, соединяющими между собой точки.
Регулярный граф — граф, степени всех вершин которого равны, то есть каждая вершина имеет одинаковое количество соседей. Например, если граф 10-регулярен, то каждая его вершина соединена ребром с 10 другими вершинами.
Гамильтонов граф — граф, содержащий гамильтонов цикл. При этом гамильтоновым циклом является такой цикл (замкнутый путь), который проходит через каждую вершину данного графа ровно по одному разу; то есть простой цикл, в который входят все вершины графа.
Полный граф Kg — граф имеющий g вершин, в котором каждая пара различных вершин смежна, то есть соединена ребром.
Подграф — граф, содержащий некое подмножество вершин исходного графа и некое подмножество инцидентных им рёбер.
Полный подграф — подграф, каждая пара вершин которого соединена ребром исходного графа.
Раскраска графа — разбиение вершин или рёбер графа на множества (называемые цветами).
(Двухцветное) число Рамсея R(n,m) — минимальное число вершин графа, двухцветная раскраска рёбер которого содержит либо полный подграф из n вершин одного цвета, либо полный подграф из m вершин другого цвета.
Таблица значений и оценок чисел Рамсея:

Формальное определение графа это математическая заумь и требует дополнительных разъяснений.
Понятнее всего граф с геометрической точки зрения: достаточно задать на плоскости наборы точек, например A,B,C,D и соединяющих их отрезков, например AB, AC, BC, CD — это и будет граф.

Если отрезки будут соединять каждую точку с каждой получится полный граф. Несколько менее интуитивна численная интерпретация графа: для приведённого выше примера вершины это четыре простых числа, рёбра — произведения соответствующих чисел. Теперь становится ясно почему задачи поиска чисел Рамсея стоят без движения: геометрически отрезок AB без дополнительной параметризации ничем не отличается от отрезка CD и приходится действовать полным перебором, а для численного подхода нужно сначала найти характеристические многочлены.
Ход решения
Числа Рамсея были записаны треугольником и сравнены треугольником Паскаля.

Стала видна область пересечения (красный треугольник на рисунке выше), а также то, что 36 (синий квадрат) это R(3,9), из чего родилась гипотеза: R(5,5)=45, R(4,6)=36, R(4,7)=49.
Предполагаемое решение основывалось на:
Хвостовой рекурсии, которая должна была «съесть» интервалы оценок до конкретного значения. Забегая вперёд, идея была верна. Ошибка в том, что «съедать» она может только в одном направлении — сверху вниз.
10-регулярном гамильтоновом графе с 45 вершинами, из которого будет построен K45. Промежуточный итог его построения:

Для рассмотрения мелких подробностей файл открывать здесь, голубые вершины графа имеют по 10 рёбер, серая 16. Для сравнения, насколько проще сделать аналогичное построение на 43 вершинах (ещё 150 рёбер должны попарно соединять фиолетовые вершины с оранжевыми, рисовать их не стал).

Довольно быстро я понял, что нужный граф построить невозможно, осознал описанную выше ошибку и после непродолжительного интернет-сёрфинга нашёл публикацию на которую сослался в начале поста. При кажущейся сложности задачи для её решения потребовалось всего три недели; необходимости чтения математических талмудов, на каждой из тысяч страниц которых формул больше чем слов, не возникло ни разу.
Happy end? Нет! За применение полученного 43 года назад результата награду скорее всего не дадут, значит необходимо двигаться дальше. На тот момент я понял природу чисел Рамсея настолько, что поиск алгоритма их нахождения занял всего два дня. Барабанная дробь!
Первый алгоритм нахождения чисел Рамсея
Предельно прост. Это сумма предыдущего числа, его квадрата и единицы: R(9,9)=432+43+1=1893 и так далее, что нетрудно доказать через теорию бифуркаций (делать это я, конечно же, не буду) или через графы (квадрат — это петля). Давайте лучше ещё раз взглянем на таблицу с числами Рамсея.

R(3,3) находится в центре квадрата с длиной стороны 5 ячеек, R(5,5) находится в его правой нижней точке, при этом 43=62+6+1. Аналогично, R(5,5) центр квадрата со стороной 9, R(9,9) его правая нижняя точка. Далее по индукции. К сожалению, алгоритм работает только в конкретном, описанном выше случае. К счастью, разложение R(9,9) на простые множители 631 и 3 явно указывает на то, что каждое неизвестное число Рамсея может быть вычислено алгоритмически.
Этих алгоритмов не более двенадцати, включая найденный.
Благодарю Михаила Ивановича Снегирёва за неоценимый вклад.
Использованные материалы:
TAKEUCHI, Kisao. Arithmetic triangle groups. J. Math. Soc. Japan 29 (1977), no. 1, 91--106.
Немного личного
Два года назад сэр Майкл Фрэнсис Атья, у которого заслуг и математических наград больше чем у Брежнева медалей, доказал гипотезу Римана, получив вместо заслуженной благодарности молчаливый скепсис математического сообщества и шквал оскорблений от физиков, самым мягким из которых было, пожалуй, «выживший из ума старый маразматик», — и ни один коллега не выступил в его защиту публично. Конечно, ведь у физики есть адронные коллайдеры, фотографии чёрных дыр и всякие другие токамаки, а у математики нет ничего. Даже цеховой солидарности и чувства собственного достоинства.
Примерно тогда же обстоятельства потребовали моего пребывания в Москве и я решил заглянуть в стекляшку с безобидным предложением: рассматривать центры чисел-близнецов как аттракторы. Дальше поста охраны меня конечно не пустили — плебсу запрещено входить в храм мудрости, для этого нужен академический документ установленного образца, «паспорт учёного», как любят называть его эти самые «учёные». Ладно, я не гордый, подошёл к рядом стоящему телефону и начал набирать внутренние номера сотрудников кафедры теории чисел — пусть санкционируют пропуск. Ни один телефон не отвечал. «Может у них конференция, семинар, коллоквиум, библиотечные дни, преподавательская работа, оппонирование, заседание, обмен опытом, диссертационный совет, отпуска, выходные, больничные, научные встречи, форум или другая академическая чепуха?» — спросил я охранника. В ответ услышал, что все на своих рабочих местах, никто никогда не берёт трубки и ничего удивительного в этом нет. Согласен, если бы я в коротких перерывах между очередным симпозиумом и международным конгрессом писал научные работы, состоящие из заголовка «Грант успешно и безрезультатно освоен, подробности ниже» и стостраничного рерайта ранее изданных учебников, то тоже бы оглох и ослеп — некогда, ctrl+c/ctrl+v само себя не нажмёт.
Так обстоят дела только в России? Нет, так везде. Большинство не желает видеть дальше собственного носа, все озабочены своими гомологиями, гомотетиями, самоцитированием и прочей ерундой. К примеру, кто систематически развивает идеи Джейкоба Лурье? Единицы. Остальные морщат носик: мы заслуженные специалисты, поэтому изучать что-то новое не можем — займёт целый год, может пострадать карьера. Тусовка эгоистична настолько, что среди миллионов(!!!) не-англоязычных математиков до сего момента не нашлось ни одного человека, готового потратить час своего драгоценного времени на перевод статьи Википедии о центрах Морли — фундаментальном результате планиметрии треугольника — с английского на язык которым говорят его дети.
Резюмируя, единственное чувство которое должен испытывать адекватный человек по отношению к большинству математиков — чувство глубочайшего презрения.
Ценный совет специалистам по теории Рамсея
Каждый из вас должен задать себе простой вопрос: чему равно количество независимых наборов рёбер графа K8? В случае ответа «двести тридцать два» необходимо незамедлительно встать, начать лупить себя по затылку и делать это до того момента, пока из головы не вылупятся все стереотипы, предрассудки и заблуждения. Это количество равно сумме всех различных функций от набора из четырех элементов до надлежащего подмножества того же набора.
Резко поумнев, можно браться за самостоятельное доказательство R(5,5)=43 через графы:
Взять три копии K4 и раскрасить их вершины, например цветами CMYK, — рёбра раскрасятся естественным образом.
Из 6 рёбер первой копии сделать соответственно раскрашенные вершины K6, 15 рёбер которого снова раскрасятся естественным образом, из них сделать 15 вершин.
Вторую и третью копии исходного K4 объединить в K8, получить раскраску 28 его рёбер, сделать из них 28 вершин.
На основе 15 предварительно раскрашенных вершин из п.2 и 28 вершин из п.3 построить K43, все 903 ребра которого вновь окажутся раскрашены оттенками всего 4 исходных.
Немного поскрипеть мозгом на тему температуры цвета или пригласить какого-нибудь художника с лекцией о тёплых и холодных оттенках, на два множества которых (чёрное-белое) и нужно разбивать рёбра получившегося графа.
Profit!
Спасибо дочитавшим, на этом на сегодня всё. Всегда ваш, Мальчег-Зайчег.


Barbaresk
Из статьи я так и не понял, оказалось ли решение математической проблемы решением проблемы материальной: «девушка приняла моё предложение и на горизонте замаячили большие расходы — свадьба штука весьма затратная.» Если да, то насколько?))