Недавно я сделал проект, в котором целевая переменная была мультиклассовой,  поэтому, я искал подходящие пути для кодирования категориальных признаков. Я нашёл множество статей, перечислявших преимущества кодирования через среднее значение целевой переменной перед другими методами, а также то, как выполнить эту задачу в двух строчках кода, используя библиотеку category_encoders . Однако, к своему удивлению, я обнаружил, что ни одна статья не продемонстрировала этого метода для мультиклассовой целевой переменной. Я просмотрел документацию category_encoders, и понял, что библиотека работает только для бинарных или вещественных переменных, посмотрел оригинальную работу  Даниэля Мисси-Баррека (Daniele Micci-Barreca), который ввел средне-целевую кодировку (mean target encoding) и так же не обнаружил ничего толкового. 

В этой статье я дам обзор документа, в котором описана кодировка по целевому признаку, и покажу на примере, как целевая кодировка работает для двоичных проблем.

Теория

Итак: если вас спрашивают «0 / 1», «кликнули / не кликнули» или «кошка / собака», то ваша проблема классификации бинарная; если вы хотите ответить «красный либо зеленый или синий, но может быть желтый» или «седан против хэчбэка и все против внедорожника», тогда проблема в нескольких классах.

Вот что вкратце говорится в упомянутой выше статье о категориальной цели:

Результат любого наблюдения можно отобразить через оценку вероятности целевой переменной.

При классификации, числовое представление будет соответствовать вероятности выпадения целевой переменной, обусловленной значением категориальной переменной.

Это эффективнее простого числового кодирования.

Для избежания переобучения при небольшом количестве наблюдений, может применяться сглаживание средних значений.

Давайте посмотрим на это практически. В бинарной задаче целью является либо 0, либо 1. В таком случае оценка вероятности для категориальной переменной может быть задана эмпирической бейесовской вероятностью P (Y = 1 | X = X_i), т.е.:

n(Y) - общее количество строк с 1 в целевой метрике,

n(i) - количество строк с i-той категории,

n(iY) - количество строк с 1 в целевой метрике в i-той категории. 

Следовательно, дробь в левой части представляет собой вероятность наличия 1 в i-той категории, а дробь в правой - вероятность наличия 1 в общих данных. ? - это функция, добавляющая монотонный вес от 0 до 1, возрастающий с увеличением n(i), который помогает при небольшом количестве наблюдений в категориях.

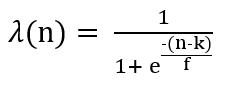
Если вы использовали TargetEncoder из библиотеки category_encoders, k - это параметр min_sample_leaf, а f - параметр сглаживания.

Введение весового коэффициента имеет смысл, когда размер выборки большой, и мы должны уделять больше внимания оценке вероятности, определяемой в левой части выражения.  Однако, если размер выборки невелик, то мы должны заменить оценку вероятности нулевой гипотезой, заданной первоначальной вероятностью зависимого атрибута (т. е. средним значением от всех Y).  С помощью такого преобразования пропущенные значения обрабатываются подобно остальным переменным.

В документе та же концепция распространяется и на мультиклассовые целевые признаки. У нас есть по одной новой функции для каждого целевого класса. Таким образом, каждая функция фактически является числовым представлением ожидаемого значения ровно одного целевого класса с учетом значения категориального признака. Конечно, количество входов может значительно увеличиться, если цель имеет очень большое количество классов, однако на практике количество значений обычно невелико. Подробнее об этом будет другая статья.

А теперь, давайте рассмотрим ситуацию с двоичной классификацией на примере.

Практика

Давайте посмотрим на пример двоичной целевой переменной.

Какова вероятность того, что целевая переменная примет значение 1, если значение признака пол «Мужской»?

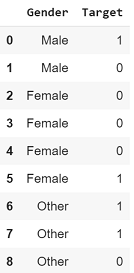
Посчитаем: 1/2 = 0,5.

Аналогичным образом, какова вероятность того, что Target будет 1, если пол «Женский»?

Посчитаем: 1/4 = 0,25.

Достаточно просто?

Теперь, если вы замените все значения «Female» на 0,25, вы рискуете так называемым переобучением. Это происходит потому, что общая вероятность единицы равна 4/9 = 0,4.

Чтобы учесть этот факт, мы добавляем вес к этой «предварительной» информации, используя формулу, из предыдущего раздела.

Установка min_sample_leaf, k = 1 и сглаживание, f = 1,

У нас есть две строки со значением «Male», поэтому n = 2;

?(‘Male’)=1/(1+exp(-(2–1)/1))=0.73    # Weight Factor for 'Male'

Target Statistic=(Weight Factor * Probability of 1 for Males)

       + ((1-Weight Factor) * Probability of 1 Overall)S(‘Male’)= (0.73 * 0.5) + ((1–0.73) * 0.4) = 0.485

Аналогично, для «Female» у нас четыре строки, поэтому n = 4;

?(‘Female’)=1/(1+exp(-(4–1)/1))=0.95 #Weight Factor for 'Female'

Target Statistic=(Weight Factor * Probability of 1 for Females)

    + ((1-Weight Factor) * Probability of 1 Overall)S(‘Female’)= (0.95 * 0.25) + ((1–0.95) * 0.4) = 0.259

Если приглядеться, можно заметить, что ? увеличивает значимость тех категорий, для которых количество строк больше. В нашем примере было 4 строки с полем «Female», и только 2 строки с полем «Male». Соответствующие весовые коэффициенты составили 0,95 и 0,73.

Таким образом, мы заменим все вхождения «Male» на 0,485 , а «Female» на 0,259. Аналогичным образом можно рассчитать значение «Другое».

Поздравляю! Вы только что реализовали вероятностную кодировку через целевой признак!

Не верите?

Убедитесь сами, запустив этот код, который делает то же самое с использованием библиотеки category_encoders:

!pip install category_encoders

import category_encoders as ce 

x=['Male','Male','Female','Female','Female','Female','Other','Other','Other']

y=[1,0,0,0,0,1,1,1,0]

print(ce.TargetEncoder().fit_transform(x,y))

Вывод

В этой статье я описал недостаток класса TargetEncoder библиотеки category_encoders. Я объяснил и резюмировал статью, в которой было введено целевое кодирование. Я объяснил на примере, как категории можно заменить числовыми значениями.

 Следующая статья будет полностью посвящена тому, как мы можем сделать то же самое для мультиклассовых целевых признаков. 

Будьте на связи!