В этой статье речь пойдет о гравитационном двигателе.
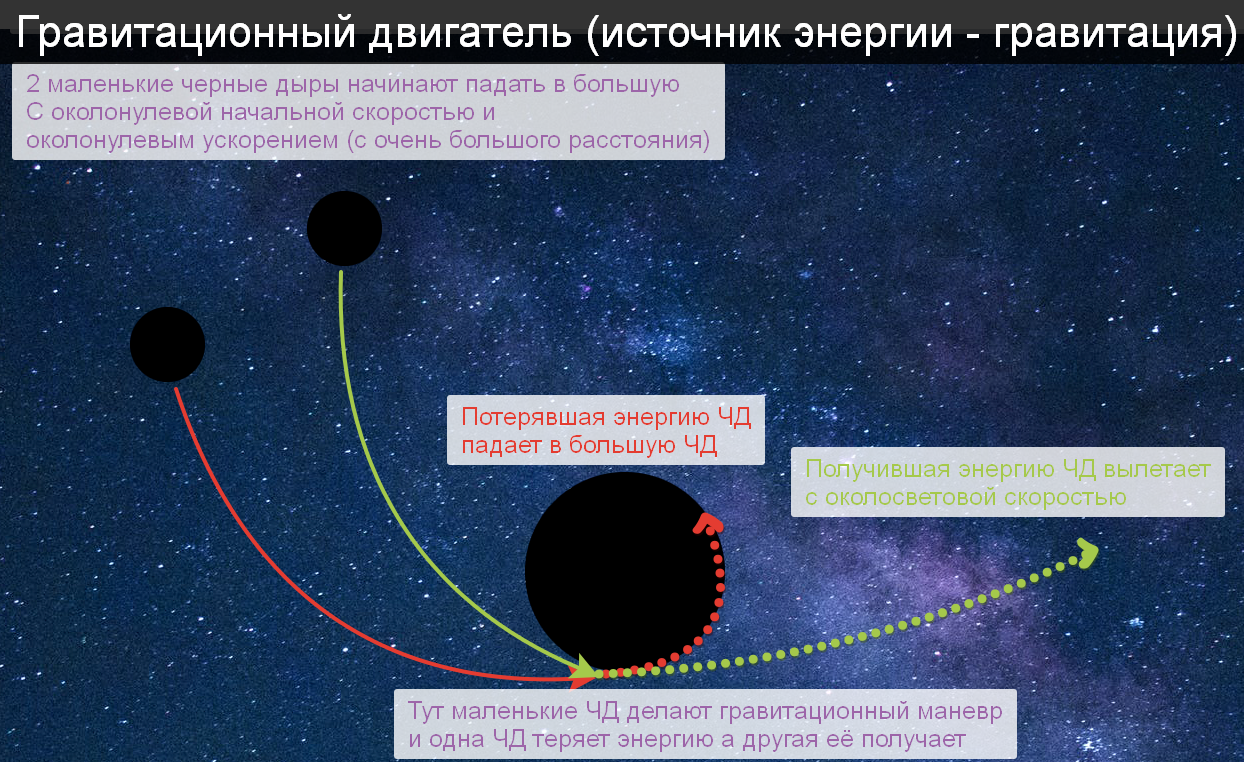
На картинке самая простая схема:
2 маленькие черные дыры издалека начинают падать в большую центральную.

Изначально никакой энергии ни у кого нет — все начинают с околонулевой скоростью.
Для примера давайте возьмем Солнечную систему и сожмем Солнце в Черную дыру.
Массу маленьких ЧД возьмем в тысячи раз меньше Солнечной — масса имеет значение, но для простоты возьмем одинаковую и незначительную относительно центральной ЧД.

Начальную скорость маленьких ЧД возьмем вторую космическую для начальной высоты, Например если мы начинаем падение с высоты Земли, то начальная скорость ~42 км/с, если начинать с высоты Юпитера, то ~18,3 км/с — т. е. Чем дальше, тем меньше начальная энергия, она может быть и 100 м/с и околонулевой, но для удобства начнем с высоты Земли и скорости ~42 км/с.

Итак: Для начала давайте бросим одну ЧД в нормальное Солнце со скоростью ~42 км/с по параболической траектории — в таком случае она подлетая к Солнцу ускоряется и около «поверхности» Солнца (695 700 километров от центра самого Солнца) разгонится до скорости ~617 км/с, пролетит рядом с «поверхностью» и начнет отдаляться/замедляться и на высоте Земли её скорость будет такая же как изначально 42 км/с.

Теперь бросаем 2 ЧД в нормальное Солнце примерно как на первой картинке. Вариантов начальных параметров очень много и можно бросать с разной начальной скоростью или разного расстояния, но мы возьмем самый простой и наглядный, одинаковая скорость, одинаковое расстояние до Солнца, но бросаем из разных начальных точек.

Итак, изначально маленькие ЧД друг с другом не связанны (расстояние между ними миллионы километров).
Они начинают каждая со скоростью 42 км/с, а при максимальном приближении к Солнцу их скорость будет ~617 км/с, и в этот же момент они приблизятся максимально близко друг к другу и сделают гравитационный маневр для перераспределения энергии.



За 1 гравитационный манёвр можно передать максимум 50% энергии, т. е. Забрать всю энергию у «сбрасываемой» ЧД за 1 раз не получится и в таком случае КПД 50%, но там очень много параметров и не вдаваясь в детали КПД 50% — это очень легко, 99% — это уже сложнее, но тем не менее тоже возможно.
Для начала давайте разберемся сколько вообще энергии можно получить таким образом (КПД как бы 100%).

Итак при сближении с Солнцем у нас 2 ЧД на скорости 617 км/с = энергией ~190 гигаджоулей на килограмм у каждой. Забираем энергию у одной и отдаем другой.
Итого ЧД без энергии как бы «ляжет» на «поверхность» Солнца с нулевой скоростью.
А ЧД получившая энергию начнет удаляться от Солнца со скоростью 872 км/с, а когда она отлетит до высоты Земли — на которой она была изначально, то её скорость составит ~618,5 км/с = энергия 191 263 МДж на каждый килограмм. А это энергия, которую можно получить при сжигании 4,3 ТОННЫ бензина!!!

Теперь просто сожмём Солнце в 100 тысяч раз (нет ничего проще — чем сжать термоядерную бомбу в активной фазе) до диаметра ~7 км — это еще не ЧД, а нейтройнная звезда. Итак масса у нас та же самая — Солнечная, и даже сама материя та же самая и ничего внутри не поменялось, поменялась только плотность, но теперь мы можем получить гораздо больше энергии и если раньше мы могли приблизится к центру масс на расстояние 696 тысяч километров и столкнулись бы с «Поверхностью» Солнца, то теперь «путь свободный» и мы можем пролететь еще сотни тысяч километров получая энергию/ускорение.

Сколько энергии можно получить около нейтронной звезды?

Около нейтронной звёзды скорость будет составлять сотни тысяч км/с (десятки процентов от скорости света) и там уже нужно учитывать эффекты Теории Относительности, а я к сожалению не «гравитолог» и кривые пространства считать не умею, но в одной из лекций Сергея Попова, он говорил, что при падении на нейтронную звезду энергия составляет 20% от $$ Т.е. Около нейтронной звезды с каждого сброшенного килограмма мы можем получить 20% от энергии, которую мы бы получили от аннигиляции 1 кг материи и антиматерии. И это от нейтройнной звезды, если мы сожмем её до черной дыры, то энергии будет больше чем 20% от $$.

Сколько максимум энергии можно получить из гравитации?

И это самый интересный и сложный вопрос. Я конечно не астрофизик, но кое что в физике и математике понимаю, а на этот вопрос я потратил часов 300 и в конечном итоге вопросов у меня стало гораздо больше чем было изначально. В общем дальше я просто расскажу свои мысли по этому поводу.

Итак, сжимаем Солнце в ЧД и получаем кристально чистый гравитационный двигатель. Никакой термодинамики, энтропии, фотонов и электронов тут нет = Электромагнитное взаимодействие тут не участвует вообще!!! -Только масса и гравитация, и при этом мы можем получить энергию. В системе из 3-х тел, где изначально нет никакой энергии и всё никуда не двигается (почти), мы можем получить массу летящую с околосветовой скоростью. Т.е. По сути, в системе из 3-х тел гравитация может отталкивать, а потенциальная энергия — это не отрицательная энергия — её можно сделать положительной.

При плотности нейтронной звезды можно получить 20% энергии от $$, у ЧД плотность выше и энергии будет больше. Минимальное расстояние пролета около звезды ограничивается поверхностью самой Звезды, у ЧД поверхности нет, но есть горизонт событий из под которого уже ничего не вытащить и забрать энергию можно только над горизонтом. А горизонт событий как раз и начинается там, где вторая космическая скорость становится равна $$. И по сути максимальная энергия, которую можно забрать у сбрасываемого тела равна энергии аннигиляции. И мы как бы можем избавиться от массы аннигилировав материю с антиматерией и получить энергию, либо мы можем сбросить массу в черную дыру (по сути в никуда) и получить ровно такую же энергию и точно так же навсегда и безвозвратно потерять массу.

Но при этом — Черные дыры гораздо «реальней» чем антиматерия, найти чистую антиматерию во вселенной вообще невозможно, а черные дыры просто валяются в вакууме. В галактике существуют двойные черные дыры вращающиеся друг вокруг друга с околосветовой скоростью образовавшиеся естественным путём.



ЧД тормозит камень ускоряется. Если для примера опять взять Солнечную систему (в центре 2 вращающиеся ЧД массой 0,5 Солнечной каждая), то мы сбрасываем с Земли 2 камня один камень остается в центре — после тормозящего гравитационного маневра он останется на орбите центра масс — вокруг которого вращаются и сами ЧД и со временем упадет в одну из ЧД, а второй ускорившийся камень, прилетит к Земле с околосветовой скоростью. Камень летящий с околосветовой скоростью — это конечно замечательно, но нам нужно электричество. Самый тупой способ получить электричество — столкнуть этот камень с Луной, т. е. Камни влетают на околосветовой скорости в Луну, она нагревается и начинает светиться как лампочка — из света получаем электричество. При столкновении на такой скорости, мощность взрыва будет в ~2 миллиона раз больше чем мощность бомбы сброшенной на Хирасиму (при массе камня, равной массе бомбы). На самом деле, способов получить электричество с помощью гравитации очень много, но пока давайте разберемся с самим источником энергии.

Тратить массу в случае нахождения 2-х Черных дыр, нам придется только для того, чтобы чёрные дыры не слились и вечно находились на одном и том же расстоянии друг от друга. Если же не «тратить» массу, а кидать камни только для ускорения, то ЧД начнут сближаться
и когда-нибудь сольются, а для получения энергии нужно обязательно две — Вернее главный элемент конструкции — это одно плотное тело с большой скоростью на орбите массивного тела, (идеал — это как раз черная дыра двигающаяся с околосветовой скоростью вокруг другой черной дыры). А если они сольются, то ЧД у нас будет всего одна, и с нулевой скоростью, поэтому нужно держать баланс. Но всё же возникает вопрос:- Сколько энергии можно забрать до того как 2 ЧД сольются? — 100% от $$, если у нас 2 ЧД по 0,5 Массы солнца, то сольются они, когда мы заберем энергию равную аннигиляции целого Солнца (зависит от изначального расстояния между ними, но даже если изначально они будут вращаться на орбите Меркурия ~ 120 млн км друг от друга, то суммарная энергия будет больше 99% от $$). На самом деле, Солнце за 5 миллиардов лет своего существования не произведет столько энергии, а за всю свою жизнь Солнце «растворит» меньше 0,1% своей массы.

Термоядерный синтез — это вообще фуфло по сравнению с тем, сколько энергии можно получить с помощью гравитации. К слову, масса ЧД совершенно не влияет на КПД = скорость около горизонта событий всегда одинаковая. И для получения энергии, по факту нам не обязательно иметь черные дыры огромной массы, по сути, масса ЧД может быть даже по 1 кг и мы можем сжать 2 арбуза до черных дыр, и всё будет работать так же как и с большими черными дырами. Причем управлять маленькими ЧД гораздо проще чем термоядерным синтезом (есть даже мнение, что удерживать материю температурой несколько миллиардов градусов вообще невозможно), а черные дыры можно держать теми же самыми гравитационными маневрами. Поэтому маленький и даже переносной реактор массой несколько килограмм вполне возможен. Правда чем меньше ЧД — тем она «злее», около горизонта событий огромные приливные силы будут разрывать любую материю и получится 2 маленьких злобных и неуправляемых квазара. В общем сбрасывать материю в маленькие ЧД плохая затея.

Можно ли сбрасывать в Черные Дыры свет?

Я конечно не специалист по кривым пространствам, но вроде бы гравитационные маневры должны работать и со светом. По крайней мере, я слышал о таком эксперименте: В институте светили «фонариком» вертикально вверх/вниз. И фотоны поднимающиеся вверх теряли энергию (краснели), а фотоны падающие вниз получали энергию (синели). Т.е. Гравитация передаёт энергию свету, а значит и гравитационные маневры со светом тоже должны работать (свет проходящий позади движения ЧД будет «ускоряться»/синеть/получать энергию, а пролетающий перед движением ЧД будет «тормозить»/краснеть/терять энергию). У света есть импульс и он может «толкать» парус, поэтому и гравитационные маневры скорее всего должны работать. Тогда энергию гравитации можно легко получать даже из очень маленьких черных дыр.

А как же излучение Хокинга?

Излучение Хокинга позволяет создать вечный двигатель, мы сбрасываем массу и получаем энергию, а она опять выходит, мы опять сбрасываем и получаем энергию, а она опять выходит. Поэтому по всем вопросам обращайтесь к самому Хокингу, а ещё лучше к тем, кто ему нобелевскую премию выдал. В моем двигателе, никакие квантовые числа не нарушаются — Всё абсолютно легально!!! Кот Шрёдингера будет доволен!!!

Хотя всё же запашок вечного двигателя тут есть. Импульс света равен $$
Чем больше частота — тем больше импульс, но «тормозящий» гравитационный маневр будет уменьшать частоту и в предельном случае, если забрать у света всю энергию около горизонта событий — то он упадет в ЧД с нулевой энергией, тогда на сколько увеличится масса ЧД?
У материи, к слову, возникает такая же проблема, если забрать всю энергию у килограммового камня перед сбросом, масса ЧД должна увеличится на 1 кг. Но второй килограммовый камень который унесёт энергию — при столкновении с Луной на околосветовой скорости, осколков из него вылетит на 2 кг. ($$ работает в обе стороны). И в результате у нас будет опять 2 кг., да еще и масса ЧД увеличится на 1 кг. Итого суммарная масса вселенной увеличится на 1 кг. И вроде бы эта проблема вообще никак не решается — суммарная масса вселенной при любом КПД будет увеличиваться.

Либо каким-то чудесным образом, при сбросе в ЧД со скоростью/энергией меньше чем $$ — масса ЧД будет уменьшаться и тогда получается, что с помощью гравитации мы можем вытаскивать энергию из ЧД.

Либо масса вселенной всё таки увеличится… но произойдет какая-нибудь дичь. Всё же бесконечно увеличивать массу мы не сможем, если мы всё это будем делать условно на орбите Земли, то со временем, горизонт событий «дотянется» до Земли, и мы просто окажемся в ЧД (энергии при этом мы не получим). И тогда бесконечно получать массу/энергию мы не сможем. Но все эти проблемы начнутся после увеличения центральной массы в миллионы раз.

В общем что это за энергия и откуда она берется вопрос весьма интересный и возможно что эта энергия вообще никак не связанна с $$ – это какая-то другая энергия и её гораздо больше. Если пойти с другой стороны и задаться вопросом — А почему вся масса вселенной не схлопнулась в огромную ЧД? — Её растолкала какая-то энергия…

P.S.

В общем Черные дыры и мутная энергия всё это конечно замечательно, но это крайне далекое будущее, да и не понятно как это будет работать с ЧД. В следующей статье поговорим о более реальных вариантах. На самом деле, даже на орбите Юпитера можно легко построить электростанцию из грязи палок и фольги — производящую 900 Мдж с каждого сброшенного килограмма, а это энергия 25 литров бензина. Вот в следующей статье я и попробую прикинуть сколько будет весить такая орбитальная конструкция.

P.P.S.

Хотелось бы еще обратится к читателям. А может кто-нибудь перевести статью на английский язык? Просто на такие статьи уходит очень много времени, да и в России физика никому особо и не нужна. Нужен хотя бы спрос. И вообще куда можно на английских ресурсах писать такие статьи?

Иногда, между состояниями ни жив ни мертв — я коллапсирую на твиче.