Вместо предисловия:

Да, наверное, нет более избитой темы, чем алгоритмы сортировки. Однако, меня в свое время так увлек процесс разбора того, какие алгоритмы задействованы в NumPy, что захотелось всем об этом рассказать. Возможно, слишком мелкая вещь, возможно, занудство какое-то, но тешу себя надеждой, что материал может быть полезным для тех, кто тему только начал! Особенно для таких же людей, как я, перешедших из смежных сфер (из телекома, например), где алгоритмы и структуры данных могут попросту не изучаться (бывает и такое). Если где-то что-то напутал (или наоборот материал оказался для вас полезным), буду рад обратной связи!

Итак, я искренне считаю, что тема реализации сортировки в рамках библиотеки NumPy - это одна из самых интересных тем по алгоритмам и структурам данных для человека, работающего с языком Python, потому что:

1. можно узнать больше о теории алгоритмов;

2. есть пример практической реализации.

Окей, звучит, наверное, как что-то на ботанском. Но дайте мне шанс - я все объясню (ниже)!

Кратко по структуре

По каждой опции я добавил:

• небольшие теоретические описания, чтобы сделать обзор более содержательным,

• и к ним же добавил работы проекта AlgoRythmics - чтобы сделать статью более наглядной (да, это те, которые танцуют всякие сортировки; и да, я прямо без ума от вещей, которые совмещают и искусство, и образование!).

  Ну, и как же без мемов (просто для удовольствия)!

  Упомянутые алгоритмы собрал по ссылке (исходные коды взяты из проекта TheAlgorithms).

Итак, какие алгоритмы сортировки предоставляет NumPy? Конечно же, идем на страницу документации (numpy.sort() method (version 1.21)):

- heapsort

- mergesort

- stable (начиная с версии 1.15.0)

- quicksort (по умолчанию)

В общем-то, не так уж и много, давайте разбираться!

heapsort

Если коротко, то алгоритм heapsort напрямую "вырастает" из двоичных куч (binary heaps - от них, собственно, и название алгоритма) и состоит из следующих шагов:

• допустим, есть массив длинною N, который должен быть отсортирован;

• данный массив преобразуется в двоичную кучу: занимает эта операция O(N*log2(N)) O(N) (UPD 28.07.21: Спасибо @makaedgar, что указал в комментариях на более эффективный способ построения двоичных куч!);

• наименьший элемент в случае min-кучи (или наибольший элемент в случае max-кучи) берется из корня: O(1);

• оставшаяся структура перестраивается, чтобы стать снова кучей: O(log2(N));

• предыдущие два шага повторяются N раз.

Общая асимптотическая сложность составляет O(N*log2(N)) (на самом деле,  O(N) + O(N*log2(N)), но меньшими слагаемыми принято пренебрегать).

Потанцуем?

Кстати, пример применения heapsort с использованием min-куч хорошо описан в документации самого Python (см. модуль heapq).

А еще в нашей литературе и переводах вы можете встретить термин "пирамидальная сортировка" - это она же, сортировка кучей, heapsort.

mergesort

На первый взгляд, перед нами классическая сортировка слиянием (mergesort), главная идея которой может быть описана древней пословицей “разделяй и властвуй”:

• сортируемый массив (или список) разбивается на две части примерно равной длины;

• каждая из частей сортируется независимо от другой (возможно, той же сортировкой слиянием, а значит снова будет разбивка на две части);

• отсортированные части соединяются в одну.

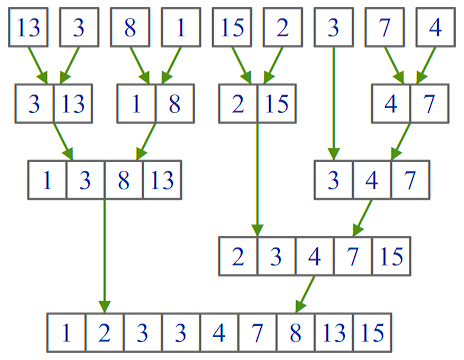
Credits: ITMO University

Несколько важных фактов о сортировке слиянием:

• асимптотическая сложность одинакова для худшего, лучшего и среднего случаев: O(N*log2(N));

• требует O(N) дополнительной памяти для сортировки массивов (но в случае связных списков, где манипуляции происходят только со ссылками на узлы, данный недостаток роли не играет);

• оптимально работает с теми структурами данных, которые обеспечивают последовательный доступ к своим элементам (например, со связными списками);

• стабильная (stable) - то есть при нахождении двух равноправных элементов оставляет их порядок в неизменном виде (имеет значение, когда сортируются, допустим, ключи ведущие к разным элементам (цены на машины - ключи, сами машины - значения) и вы хотите оставить порядок изначального массива или списка по возможности не тронутым).

На первый взгляд... Однако, что говорит нам документация:

New in version 1.17.0.

Timsort is added for better performance on already or nearly sorted data. On random data timsort is almost identical to mergesort. It is now used for stable sort while quicksort is still the default sort if none is chosen. For timsort details, refer to CPython listsort.txt. ‘mergesort’ and ‘stable’ are mapped to radix sort for integer data types. Radix sort is an O(n) sort instead of O(n log n).

То есть:

1. Опции mergesort и stable обозначают одно и тоже в рамках numpy.sort();

2. Гибридная сортировка Timsort используется вместо “чистой” mergesort (такая же, как в методе sort() и функции sorted() CPython);

3. Если элементы сортируемого массива - это целые числа (int), то применяется вообще поразрядная сортировка (radix sort), занимающая O(N) времени (просто "отвал башки"!).

А гибридная Timsort, потому что совмещает в себе сортировку вставками (insertion sort) и сортировку слиянием (подробно см. здесь: CPython listsort.txt).

Итак, получается, что само название опции (mergesort) - это скорее пример наследия в целях обратной совместимости. "Под капотом" происходят более сложные вещи.

quicksort

Начнем с азов. Если коротко, то классическая быстрая сортировка (quicksort):

• выбирает опорный (pivot) элемент;

• разбивает массив на три группы: “меньше”, “больше” и “равно” опорного(ому) элемента(у);

• рекурсивно применяет себя саму же к полученным группам.

Несколько фактов о быстрой сортировке:

• средняя асимптотическая сложность: O(N*log2(N));

• худшая асимптотическая сложность: O(N²);

• требует относительно малого количества дополнительной памяти: O(log2(N));

• часть стандартной библиотеки языка C (qsort());

• не является стабильной.

Однако! На самом деле, сейчас данная опция тоже обозначает другой алгоритм сортировки:

New in version 1.12.0.

quicksort has been changed to introsort. When sorting does not make enough progress it switches to heapsort. This implementation makes quicksort O(n*log(n)) in the worst case.

То есть, опция быстрой сортировки означает гибридный алгоритм introsort, который использует либо быструю сортировку, либо пирамидальную сортировку в зависимости от обстоятельств (обычно это зависит от глубины рекурсии быстрой сортировки - если она слишком большая, то имеет смысл переключиться).

Здесь может возникнуть вопрос, а зачем тогда оставили чистую heapsort? Я вот задался этим вопросом, но думаю разгадка тривиальна: для обратной совместимости.

Заключение

Подведем итоги:

1. Теория: чтение документации о том, как и какие реализованы алгоритмы сортировки в рамках библиотеки NumPy - это хороший повод изучить несколько простых и гибридных алгоритмов.

2. Практика: чтение документации о том, как и какие реализованы алгоритмы сортировки в рамках библиотеки NumPy позволяет проследить, как простые подходы усложняются, развиваются в гибридные и находят применение в популярных реализациях, используемых инженерами и учеными по всему Миру (отметим, что метод pandas.DataFrame.sort_values использует тот же пул алгоритмов).

Надеюсь, мой небольшой обзор был вам полезен, и да пребудет с вами сила документации!

P.S.

И да, на практике, вы скорее всего будете использовать опцию stable (или mergesort по старинке), если вам нужна будет стабильная сортировка; или оставите параметр незаполненным (и тогда по умолчанию будет quicksort, которая на самом деле introsort), если стабильная сортировка не нужна - и всё. Но, согласитесь, как же приятно бывает в чем-то разобраться!

Литература

1. Стивенс, Р., 2016. Алгоритмы. Разработка и применение. М.: Издательство «Э.

2. Седжвик, Р., 2001. Фундаментальные алгоритмы на С++. К.: Диасофт.

Ресурсы для визуализации алгоритмов

1. SORTING.at

2. Sorting Algorithms Animations

3. Min Heap sort

Полезные ссылки

1. Описание алгоритмов сортировки и сравнение их производительности

2. Основные виды сортировок и примеры их реализации

Версии статьи

1. NumPy sorting (and dancing and memes) (Medium)

2. NumPy sorting (and dancing and memes): ​ a short review for students​ (SlideShare)