21.05.2019 17:39
ritchie_kyoto 0 1100 Источник

Чтобы передать сообщение от базовой станции мобильному устройству (и наоборот), электромагнитной волне приходится преодолевать значительное количество препон: отражения, преломления, рассеивания, затенения, доплеровские смещения частот и так далее. Во-первых, все эти воздействия принято называть мультипликативными (от англ. multiplication — умножение) — по математической модели таких воздействий. А, во-вторых, можно собрать под общим термином замирания (fading).


От стандарта к стандарту, от поколения к поколению, от технологии к технологии ученые и инженеры бились и бьются над проблемой нивелирования этих замираний (fading mitigation).


И некоторые решения нашли широкое распространение. Скажем больше: почти все из них, так или иначе, связаны с понятием разнесения (diversity).



Источник иллюстрации (нет, это не реклама, просто удачное сочетание нужного термина и кота).

Пример таких решений:


  1. Frequency hopping — против частотно-селективных замираний;
  2. Оценка и выравнивание канала (channel estimation and equalization) через обратную связь — GSM, для подавления изменений во временной области;
  3. Расширение спектра (UMTS);
  4. Пилотные сигналы (начиная с UMTS) по нисходящему каналу (Down-link) и сопровождение сигнала (signal tracking) по восходящему каналу (Up-link) — для подавления изменений во временной области;
  5. OFDM — LTE, против частотно-селективных замираний;
  6. Временное разнесение (помехоустойчивое кодирование);
  7. Поляризационное разнесение (на стороне передатчика) + Сумматоры (combiners, на стороне приёмника);
  8. Пространственное разнесение.

Последнюю из упомянутых техник мы рассмотрим сегодня в рамках ещё одной темы по MIMO.


Space diversity order и array gain


Первое.


Есть такое понятие — порядок пространственного разнесения (space diversity order): если одна и та же информация может быть собрана с разных направлений, то надежда восстановить её правильно увеличится. В качестве примера из жизни, можно представить сбор информации об одном и том же событии от независимых друг от друга источников-информаторов. В радиосвязи этот порядок мы можем увеличить, в том числе, применяя MISO, SIMO или MIMO.


Теоретический предел такого разнесения M_TM_R, где M_T — количество передающих антенн, а M_R — количество приёмных антенн. Запомним это.


div

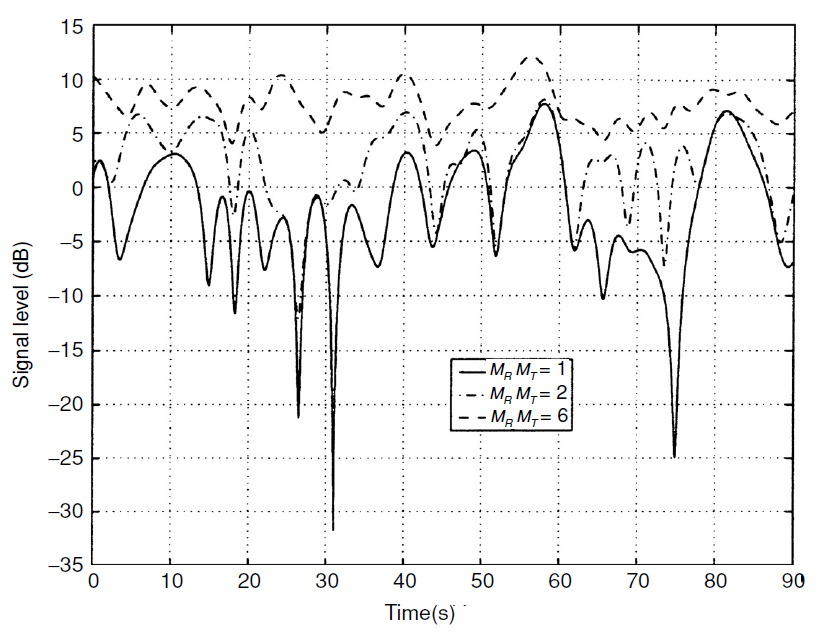
Рис.1. Стабильность канала, вызванная увеличением порядка пространственного разнесения. При значениях M_TM_R \to \infty канал полностью стабилизируется и превратится в канал без замираний (AWGN) [1, p.101].


Второе.


Используя SIMO, MIMO и даже MISO (в случае известного канала), можно получить, так называемое, усиление массива (array gain). Это означает, что применение нескольких приемных антенн и/или правильное распределение энергии на передающей стороне позволяет увеличить отношение сигнал/шум (SNR) — а значит снизит количество ошибок.


Порядки разнесения и усиления массива для различных конфигураций можно вывести аналитически [1, c. 86 — 100] и свести в одну таблицу [1, c. 101] и для случая, когда канал неизвестен (CU — Channel Unknown), и для случая, когда канал известен (CK — Channel Known) на стороне передатчика.


Конфигурация Diversity order Array gain
SIMO (CU, Rx-MRC) M_R M_R
SIMO (CK, Rx-MRC) M_R M_R
MISO (CU, OSTBC) M_T 1
MISO (CK, Tx-MRC) M_T M_T
MIMO (CU, OSTBC) M_TM_R M_R
MIMO (CK, DET) M_TM_R M_TM_R

Окей, пусть широкими мазками, но теперь у нас есть хоть какое-то понимание теоретических аспектов подавления замираний. Следующий вопрос — как достичь этих теоретических пределов? Какие существуют техники активации рассмотренных выигрышей?


Решение №1. Пространственно-временные коды


Одним из самых популярных классов решений по пространственному разнесению является, пожалуй, класс пространственно-временных кодов (space-time codes). Например, знакомый, я думаю, многим метод Аламоути (пример блочного кода) [2, c. 40-46]:


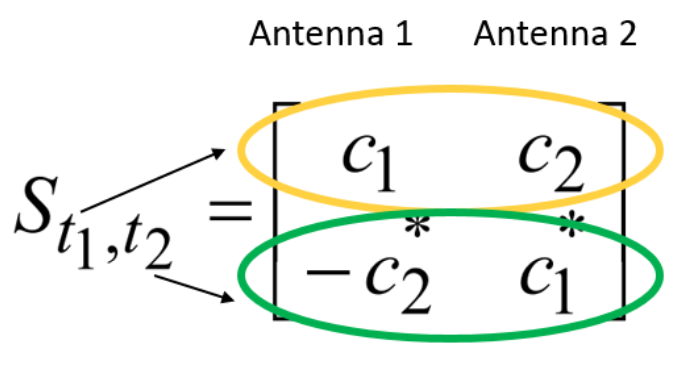
AlamF

где c_i при i=1,2 — это некоторые входные символы, t_i при i=1,2 — это временные отсчеты (time slots), а \mathbf{S} — это, собственно, матрица кодирования.


Схема Аламоути ортогональна [1, с.93-95, 97-98] и, что самое важное, не требует информации о состоянии канала (Channel State Information).


Математическое описание передачи кодированного по схеме Аламоути сигнала, а также несколько примеров моделирования этой техники в MatLab можно найти в моём репозитории. Интересующимся добро пожаловать!

Однако, как вы можете заметить, схема Аламоути — это случай, когда у нас есть только две передающие антенны (M_T = 2).
Но не стоит падать духом раньше времени: доступны, конечно, и другие варианты, просто называются они немного иначе. Например, согласно [3] можно применить такие схемы кодирования:


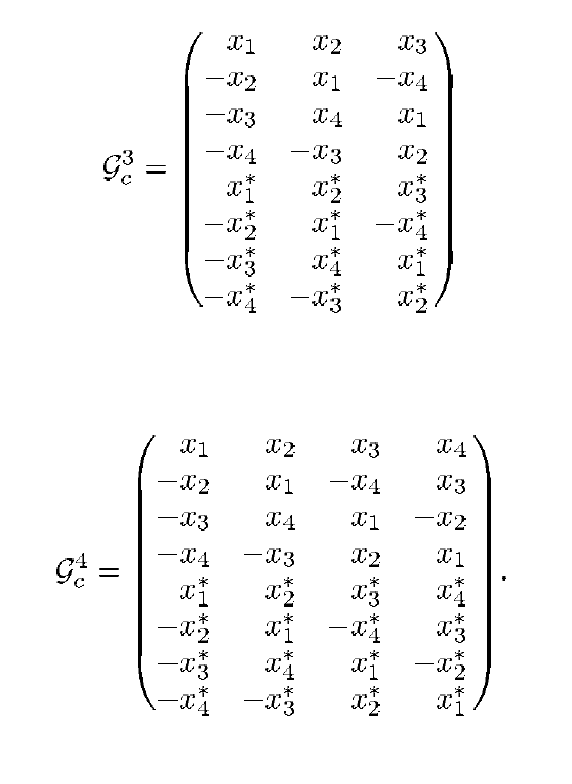
Tarokh

Рис. 2. Схемы передачи для случаев M_T = 3 и M_T = 4 [2].


И ещё много других вариантов: лишь бы отвечали условиям ортогональности.


Для таких кодов требуются, собственно, те же процедуры для кодирования и декодирования, что и для кода Аламоути. Поэтому объединяются они обычно под общим термином ортогональные пространственно-временные блочные коды (OSTBC — Ortogonal Space-Time Block Codes).


Достаточно большое внимание этому классу кодов уделено в материалах "Introduction to MIMO Systems" от компании MathWorks. Всем заинтересованным настоятельно советую ознакомиться!

Какова цена?


Как это видно из схемы передачи, мы хоть и передаём символы параллельно, но тратим на это несколько временных слотов. Следовательно, мы жертвуем пропускной способностью (как минимум, недополучаем её). Для схемы Аламоути такой компромисс симметричен: задействуем 2 антенны и 2 временных слота (будто бы используем SISO с точки зрения пропускной способности). Другие схемы могут влиять на скорость передачи ещё сильнее.


Решение №2. DET: Dominant Eigenmode Transmission


Хорошо, для предыдущего класса техник знания о канале нам важны не были. А что если эти знания у нас всё-таки есть? Нет ли в таком случае более подходящих техник?


В одной из предыдущих моих статей мы обсуждали, что, имея на руках знания о состоянии канала, мы можем применять различные методы обработки сигналов, чтобы увеличить пропускную способность. Этот же принцип работает и для повышения помехоустойчивости.


Наверное, многие слышали про метод MRC и многие знают, что метод этот как нельзя кстати подходит для случая SIMO, когда на передаче антенна хоть и одна, но на приёме их все-таки много, а значит есть из чего комбинировать.


Но, наверное, уже меньшее количество читателей сталкивалось с MRC на передающей стороне (Tx-MRC) [1, c. 95,96], и ещё меньше с технологией DET (Dominant Eigenmode Transmission) [1, c. 98-100]. Исправим!


Для начала рассмотрим общий случай MIMO канала и последний из названных методов — DET.


В чём суть:


  • Если у передатчика имеется матрица \mathbf{H}, то её можно обработать.
  • Например, разложить её через SVD: \mathbf{H} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^H, получив таким образом несколько матриц определенного свойства.
  • Эти свойства можно использовать для оптимизации передачи, например, применив предварительное кодирование (pre-coding).

Введём некоторый пре-кодирующий вектор:


\underset{M_T\times1} {\mathbf{w}} = \sqrt{M_T}\underset{M_T\times1} {\mathbf{v}_1}

где \mathbf{v}_1 — это первый (доминирующий, так сказать) вектор матрицы \mathbf{V}.


Более того, мы можем записать и вектор пост-обработки (post-processing):


\underset{M_R\times1} {\mathbf{g}} = \underset{M_R\times1} {\mathbf{u}_1}

где \mathbf{u}_1 — это первый вектор матрицы \mathbf{U}.


Переопределим модель принятого сигнала (см. тему пропускной способности):


{z} = \underset{1\times M_R} {\mathbf{g}^H} \underset{M_R\times 1} {\mathbf{y}} = \mathbf{g}^H \sqrt{\frac{E_s}{M_T}}\mathbf{H}\mathbf{w}s + \mathbf{g}^H\mathbf{n} = \sqrt{E_s}\mathbf{u}_1^H \mathbf{H} \mathbf{v}_1 s + \hat{\mathbf{n}} = \sqrt{E_s} \sigma_{max} s + \hat{\mathbf{n}}

Вуаля! Магия линейной алгебры выделила среди всех путей распространения самый выгодный и всю энергию направила туда. Фактически, перед нами линейный алгоритм диаграммообразования (beamforming).


Ценой рассмотренного подхода всё также, как и в случае OSTBC, является ограничение пропускной способности. Правда, происходит это теперь сугубо в пространственной области.


Почему же метод содержит в своём названии собственные числа (eigen values), если разговаривали мы только о сингулярных?

Потому что собственные числа (мощности путей распространения — замираний) могут быть напрямую выведены из сингулярных чисел (амплитуды замираний):


\mathbf{R}_{\mathbf{HH}^H} = \mathbf{HH}^H = \mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^H = \mathbf{Q} \begin{bmatrix} \lambda_{max} & & & &\ & . & & & \ & & . & & \& & & . & \& & & & \lambda_{min}\\end{bmatrix} \mathbf{Q}^H

Хорошо, с DET более или менее понятно — что с Tx-MRC?


С ним всё ещё проще — это частный случай DET, и сейчас мы это докажем.


Для Tx-MRC в литературе предложен следующий вектор пре-кодирования:


\mathbf{w} = \sqrt{M_T} \frac{\mathbf{h}^H}{\sqrt{||\mathbf{h}||^2_F}}

Держим в голове, что квадрат нормы Фробениуса равен собственному числу и, соответственно, квадрату сингулярного числа ||\mathbf{h}||^2_F = \lambda_{max} = \sigma^2_{max} (в случае SIMO и MISO).


Тогда снова переопределим модель принятого сигнала, только уже для MISO случая:


y = \sqrt{\frac{E_s}{M_T}} \mathbf{h} \mathbf{w} s + \mathbf{n} = \sqrt{\frac{E_s}{M_T}} \mathbf{h} \sqrt{M_T} \frac{\mathbf{h}^H}{\sqrt{||\mathbf{h}||^2_F}} s + \mathbf{n}} = \frac{\sqrt{E_s}}{\sigma_{max}} \mathbf{h} \mathbf{h}^H s + \mathbf{n}} = \frac{\sqrt{E_s}}{\sigma_{max}} ||\mathbf{h}||_F^2 s + \mathbf{n}} = \frac{\sqrt{E_s}}{\sigma_{max}} \lambda_{max} s + \mathbf{n}} = \sqrt{E_s} \sigma_{max} s + \mathbf{n}}

Что и требовалось доказать.


Заметьте, теперь мы говорим не просто о разнесении сигналов на передающей стороне и комбинировании их на стороне приёмной, как это было в случае с OSTBC. Теперь речь идет об оптимальном распределении энергии. А значит и значения array gain в данном случае выше, чем у OSTBC.

Теперь, когда все слова сказаны, попробуем промоделировать наши техники.


Моделирование


Сегодня я немного считерил: для моделирования OSTBC использованы готовые объекты из Communication Toolbox (MatLab R2014a — уж какой был):



Для модуляции и демодуляции (и подсчета битовой ошибки — BER) были использованы уже не объекты, а функции. Их аналоги есть в пакете communications Octave.


Исходные коды можно посмотреть здесь.
clear all; close all; clc

snapshots = 100000;
EbNo = 0:15;
M = 2; % modulation order (BPSK)
Mt = 2; % num. of Tx antennas
Mr = [1; 2]; % num. of Rx antennas

ostbcEnc = comm.OSTBCEncoder('NumTransmitAntennas', Mt); % for Alamouti

ric_ber = zeros(length(EbNo), length(M), length(Mr));
sum_BER_alam = zeros(length(EbNo), length(M), length(Mr));
sum_BER_det = zeros(length(EbNo), length(M), length(Mr));

for mr = 1:length(Mr)
    ostbcComb = comm.OSTBCCombiner('NumTransmitAntennas', Mt, 'NumReceiveAntennas', Mr(mr));
    H = zeros(Mr(mr), Mt, snapshots);
    alam_fad_msg = zeros(snapshots, Mr(mr));
        for m = 1:length(M)

            ric_ber(:,m,mr) = berfading(EbNo, 'psk', M(m), Mr(mr)*Mt, 0);

            snr = EbNo+10*log10(log2(M(m))); % Signal-to-Noise Ratio
            message = randi([0, M(m)-1],100000,1);

            mod_msg = pskmod(message, M(m), 0, 'gray');
            Es = mean(abs(mod_msg).^2); % symbol energy

            alam_msg = step(ostbcEnc, mod_msg); % OSTBC encoding

            % Channel
            h = (1/sqrt(2))*(randn(Mr(mr),Mt,snapshots/Mt)...
            + 1j*randn(Mr(mr),Mt, snapshots/Mt)); % Rayleigh flat fading

            % Channel is stable during to time-slots: 
            H(:,:,1:2:end-1) = h;
            H(:,:,2:2:end) = h;

            pathGainself = permute(H,[3,2,1]);

            % Transmit through the channel (Alamouti):
            for q = 1:snapshots;  
                alam_fad_msg(q,:) = (sqrt(Es/Mt)*H(:,:,q)*alam_msg(q,:).').';
            end

            % DET:
            sigmas = zeros(length(mod_msg), 1);
            for hi = 1:length(mod_msg)
                [U, Sigma, Vh] = svd(H(:, :, hi));
                sigmas(hi) = Sigma(1, 1);
            end

            det_fad_msg = mod_msg.*sigmas;

            No = Es./((10.^(EbNo./10))*log2(M(m))); % Noise spectrum density
            for c = 1:500
                for jj = 1:length(EbNo)
                    alam_noisy_msg = alam_fad_msg + ... 
                        sqrt(No(jj)/2)*(randn(size(alam_fad_msg)) + ...
                        1j*randn(size(alam_fad_msg))); % AWGN 
                    alam_decodeData = step(ostbcComb,alam_noisy_msg,pathGainself); %OSTBC combining
                    alam_demod_msg = pskdemod(alam_decodeData, M(m), 0, 'gray'); % demodulation
                    [number,alam_BER(c,jj)] = biterr(message, alam_demod_msg); % BER

                    det_noisy_msg = det_fad_msg+ ... 
                        sqrt(No(jj)/2)*(randn(size(mod_msg)) + ...
                        1j*randn(size(mod_msg))); %AWGN 
                    det_decodeData = det_noisy_msg./sigmas; % Zero-Forcing equalization
                    det_demod_msg = pskdemod(det_decodeData, M(m), 0, 'gray'); % demodulation
                    [number,det_BER(c,jj)] = biterr(message, det_demod_msg); % BER
                end
            end
            sum_BER_alam(:,m, mr) = sum(alam_BER)./c;
            sum_BER_det(:,m, mr) = sum(det_BER)./c;
        end
end

figure(1)

semilogy(EbNo, sum_BER_alam(:, 1, 1), 'b-o', ...
         EbNo, sum_BER_det(:,1,1), 'b->',...
         EbNo, ric_ber(:,1,1), 'b-',...
         EbNo, sum_BER_alam(:, 1, 2), 'r-o', ...
         EbNo, sum_BER_det(:,1,2), 'r->',...
         EbNo, ric_ber(:,1,2), 'r-',...
         'LineWidth', 1.5)
title('BPSK (Rayleigh flat fading)')
legend('Alamouti (2x1)','Tx-MRC (2x1)','2-nd order diversity', ...
        'Alamouti (2x2)','DET (2x2)','4-th order diversity')
xlabel('EbNo (dB)') 
ylabel('BER') 
grid on

Получиться должно что-то такое:



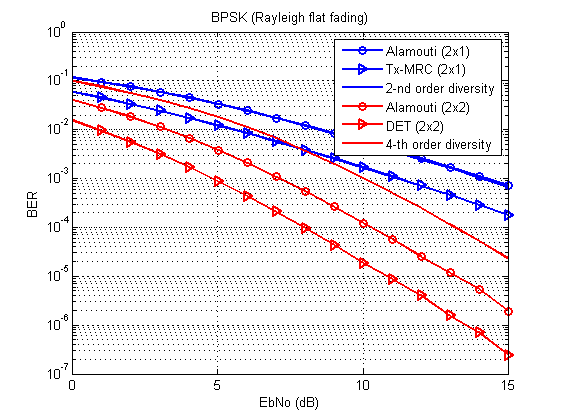
Рис. 3. Кривые битовых / символьных ошибок для разных техник передачи (BPSK, Рэлеевский канал с плоскими замираниями). Сравните с [1, c. 96, 100].


А теперь вопрос: а где же кривая теоретической границы разнесения второго порядка?


Ответ

Всё согласно таблице: эта кривая полностью совпадает с Аламоути 2x1. В случае MIMO в игру вступает ещё и array gain, и поэтому кривые разделены.


Так или иначе, а DET (или Tx-MRC) ожидаемо опережают Аламоути по качеству.


Вот так: знание — сила!


Литература


  1. Paulraj, Arogyaswami, Rohit Nabar, and Dhananjay Gore. Introduction to space-time wireless communications. Cambridge university press, 2003.


  2. Бакулин М. Г., Варукина Л. А., Крейнделин В. Б. Технология MIMO: принципы и алгоритмы //М.: Горячая линия–Телеком. – 2014. – Т. 244.


  3. Tarokh, V., Jafarkhani, H., & Calderbank, A. R. (1999). Space-time block codes from orthogonal designs. IEEE Transactions on Information theory, 45(5), 1456-1467.



P.S.


Преподавательскому составу и студенческой братии родной специальности передаю привет!

Комментарии (0)