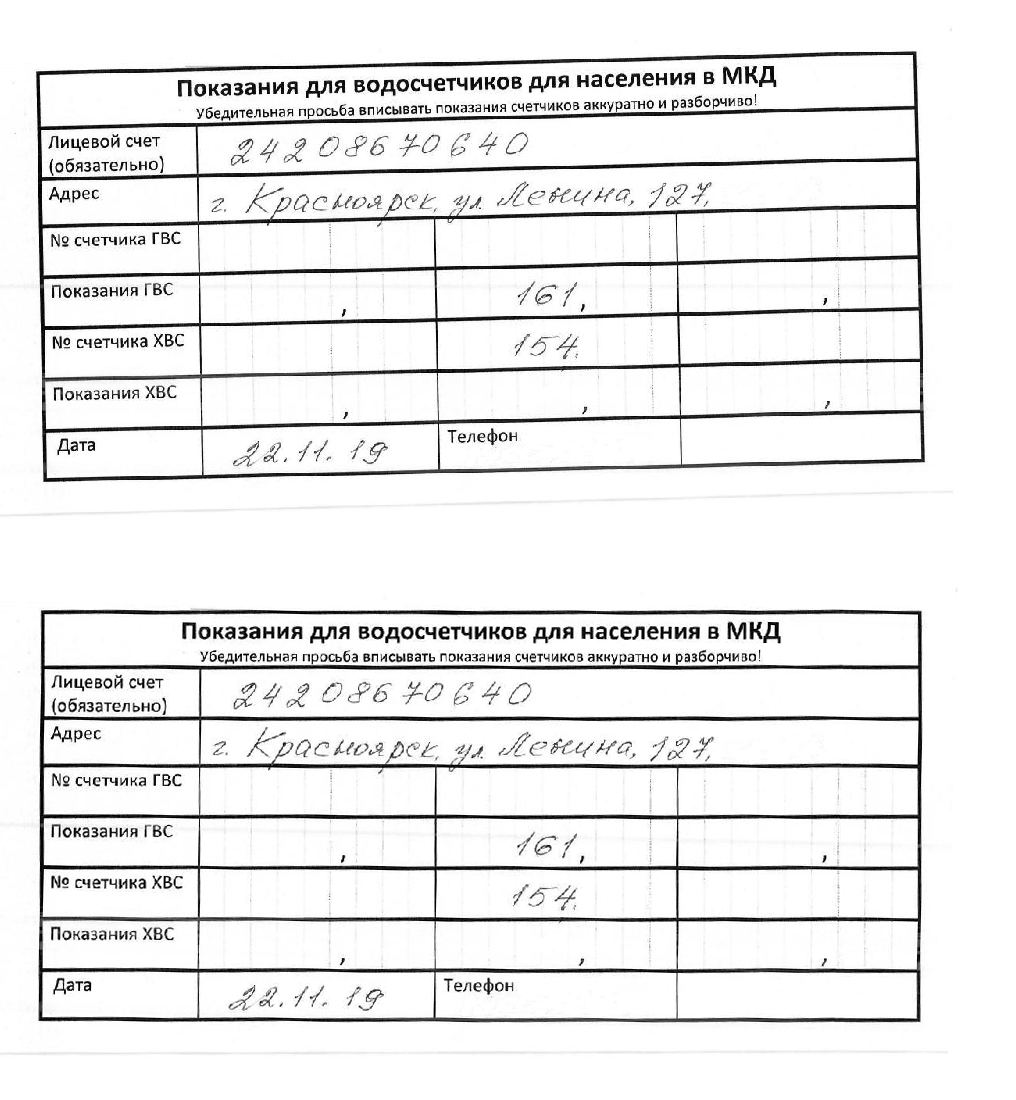
Привет, Хабр! В этой статье я расскажу о том, как восстановить структуру таблицы и извлечь рукописные числа из отсканированного документа такого плана:

Алгоритм

Допустим, у нас есть документ , который представлен выше, и в нём необходимо извлечь данные из тех ячеек, в которых имеются числа. Ячейки, в которых могут содержаться числа выделены красным цветом:

Для того, чтобы распознать информацию в ячейках, необходимо проделать следующие шаги:

1. Коррекция перекоса таблицы — в нашем случае это не так критично, так как у нас угол перекоса не очень большой, но если угол перекоса будет достаточно большой(от 10 градусов), в таком случае может возникнуть много трудностей при распознавании информации.

2. Восстановление структуры таблицы, то есть нахождения ограничительных рамок каждой ячейки.

3. Поиск нужных полей в таблице, то есть тех полей, в которых есть числа.

4. Распознавание рукописных чисел в ячейках.

Коррекция перекоса таблицы

img = cv2.imread(image_name)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
_, img_bin = cv2.threshold(gray, 128, 255,
                           cv2.THRESH_BINARY_INV)

Первым делом мы переводим наше изображение в оттенки серого и преобразуем серое изображение в бинарное с помощью функции threshold(), про которую я подробно писал тут .

coords = np.column_stack(np.where(img_bin == 255))
angle = cv2.minAreaRect(coords)[-1]

Теперь в функцию where() мы передаём чёрно-белое изображение, и берём координаты тех пикселей, у которых значения равны 255 . Эта функция возвращает нам два массива — координаты по оси y и x соответственно, поэтому с помощью функции column_stack() мы складываем два одномерных массива в виде столбцов, чтобы получить один двумерный массив. Далее этот массив мы передаём в функцию minAreaRect(), которая находит минимальную площадь повёрнутого прямоугольника и возвращает последним аргументом угол поворота. Теперь нам известен угол наклона, поэтому мы применяем аффинное преобразование для исправления перекоса:

(h, w) = img.shape[:2]
center = (w // 2, h // 2)
rotation_matrix = cv2.getRotationMatrix2D(center, angle, 1.0)
rotated = cv2.warpAffine(img, rotation_matrix, (w, h),
          flags=cv2.INTER_CUBIC, borderMode=cv2.BORDER_REPLICATE)

Мы передаём координаты точки вокруг которой будем вращаться, в нашем случае, это координаты центра, угол наклона и коэффициент масштабирования в функцию getRotationMatrix2D(). Данная функция возвращает массив numpy, который мы передаём вторым аргументом в функцию warpAffine(), которая выполняет преобразование. Сверху — изображение до, снизу — изображение после:

Восстановление структуры таблицы

Для того, чтобы восстановить структуру таблицы, нам необходимо воспользоваться методами математической морфологии такими как эрозия и наращивание:

if type == 'h':
    structuring_element = np.ones((1, 50), np.uint8)
elif type == 'v':
    structuring_element = np.ones((50, 1), np.uint8)
erode_image = cv2.erode(img_bin, structuring_element, iterations=1)
dilate_image = cv2.dilate(erode_image, structuring_element, iterations=1)

Эрозия(erode): прилагаем к каждой точке объекта на оригинальном изображении структурный элемент так, чтобы совпадал центр структурного элемента и точка на изображении, если структурный элемент полностью принадлежит объекту, то такая точка остается => удаляются детали, которые меньше чем структурный элемент и объект становится тоньше.

Наращивание (dilate): на каждую точку объекта накладывается структурный элемент, а недостающие точки дорисовываются => закрашиваются дырки меньшие, чем структурный элемент, а объект в целом становится толще.

В результате у нас получились следующие вертикальные и горизонтальные линии соответственно:

Далее полученные линии складываем и применяем к полученном изображению функцию dilate():

def merge_lines(horizontal_lines, vertical_lines):
    structuring_element = np.ones((3, 3), np.uint8)
    merge_image = horizontal_lines + vertical_lines
    merge_image = cv2.dilate(merge_image, structuring_element, iterations=2)
    return merge_image

В итоге восстановить структуру таблицы удалось:

Поиск необходимых полей в таблице

Теперь создадим словарь, где в качестве ключа будет выступать название колонки, а в качестве значения- True/False , True — те ячейки, в которых могут содержаться числа, False — это соответственно те поля, в которых информацию мы не собираемся распознавать. В дальнейшем для ключей, у которых значение True, информацию будем обновлять распознанными числами:

document_columns_dict = {
    "Name_0": False, "Account_0": False, "Account_1": True,
    "Adress_0": False, "Adress_1": False, "Number_GVS_0": False,
    "Number_GVS_1": True, "Number_GVS_2": True, "Number_GVS_3": True,
    "GVS_0": False, "GVS_1": True, "GVS_2": True, "GVS_3": True,
    "NUMBER_XVS_0": False, "NUMBER_XVS_1": True, "NUMBER_XVS_2": True,
    "NUMBER_XVS_3": True, "XVS_0": False, "XVS_1": True, "XVS_2": True,
    "XVS_3": True, "Date&Phone_0": False, "Date&Phone_1": False,
    "Date&Phone_2": False, "Date&Phone_3": False}

Далее необходимо найти контуры каждой колонки, что мы и делаем с помощью функции findContours(). Полученные контуры нам необходимо отсортировать в таком порядке, в котором идут пары «ключ-значение» в словаре, то есть сверху вниз и слева направо:

bounding_boxes = [cv2.boundingRect(c) for c in cnts]
if method == "top-to-right":
    bounding_boxes.sort(key=functools.cmp_to_key(lambda s, 
                                                 t: custom_tuple_sorting(s, t, 4)))

Сперва с помощью функции boundingRect() находим ограничительные рамки каждого контура: начальные x и y координаты, за которыми следуют ширина и высота рамки. В 3 строчке кода мы сортируем контуры с помощью функции custom_tuple_sorting(), реализацию которой Вы можете посмотреть на github . Данная функция сортирует контуры сначала по у, а потом по x. В качестве первых двух аргументов функция принимает координаты контура, а последним — смещение. Дело в том, что ячейки могут располагаться в одной строке, но координаты по y могут немного отличаться, поэтому, если разница между двумя координатами меньше смещения, то мы считаем такие координаты равными между собой. То есть, если смещение равно 3, то 34=35=36.

Следующим шагом мы вырезаем только ту ячейку с основного изображения, у которой значение в словаре True:

if list(document_columns_dict.values())[count]:
    img_crop = rotated_image[y - 12:y + h + 12,
                             x - 6:x + w + 6]

Находим ограничительные рамки чисел:

Как мы можем увидеть, у нас появилось две проблемы:

• Нашлись не все контуры чисел. Это связано с тем, что числа были написаны слишком близко к нижней линии ограничительной рамки.

• У последней цифры образовалось два контура.

Для того, чтобы решить первую проблему необходимо найти и заменить все пиксели ограничительной рамки ячейки белыми пикселями. Для этого мы вырезаем такой же кусок изображения только с изображения, которое нам вернула функция merge_lines(), где линии ограничительной рамки белого цвета:

Данное изображение мы передаём в функцию find_cell_contours(), где в качестве первого аргумента выступает предыдущее изображение, а вторым аргументом — изображение, которое было вырезано с основного изображения. В первой строчке кода мы находим координаты всех белых пикселей у изображения, которое было передано первым в функцию и в цикле заменяем цвет на белый у изображения, которое было передано в качестве второго аргумента, только для тех пикселей, которые были белыми у первого изображения:

def find_cell_contours(frame_image, crop_image):
    white_pixels = np.where(frame_image == 255)
    y = white_pixels[0]
    x = white_pixels[1]
    for i in range(len(y)):
        crop_image[y[i]][x[i]] = 255
    return crop_image

Для того, чтобы решить вторую проблему, мы с помощью функции permutations() модуля itertools перебираем все возможные комбинации контуров и если оно соответствует условию в 3 строчке кода => контур находится внутри контура и мы такой контур удаляем:

def detect_contour_in_contours(all_contours):
    for rec1, rec2 in itertools.permutations(all_contours, 2):
        if rec2[0] >= rec1[0] and rec2[1] >= rec1[1] 
        and rec2[2] <= rec1[2] and rec2[3] <= rec1[3]:
            in_rec = [rec2[0], rec2[1], rec2[2], rec2[3]]
            all_contours.remove(in_rec)
    return all_contours

После всех вышеперечисленных действий удалось решить проблему и получилось следующее изображение:

Распознавание рукописных чисел в ячейках

На этом этапе я не буду останавливаться подробно. Была обучена свёрточная нейронная сеть . Датасет был взят отсюда . В конечном итоге, для изображения, которое было приведено в начале статьи у нас получился вот такой словарик:

{'Name_0': False, 'Account_0': False, 'Account_1': '4204351220', 
 'Adress_0': False, 'Adress_1': False, 'Number_GVS_0': False, 
 'Number_GVS_1': '2353777',  'Number_GVS_2': '', 'Number_GVS_3': '',
 'GVS_0': False, 'GVS_1': '16', 'GVS_2': '', 'GVS_3': '',
 'NUMBER_XVS_0': False, 'NUMBER_XVS_1': '803',  'NUMBER_XVS_2': '', 
 'NUMBER_XVS_3': '', 'XVS_0': False, 'XVS_1': '41', 'XVS_2': '', 
 'XVS_3': '', 'Date&Phone_0': False, 'Date&Phone_1': False, 
 'Date&Phone_2': False, 'Date&Phone_3': False}

Заключение

Я надеюсь, вам понравилась моя статья, а знания пригодятся для разработки программы по анализу собственных документов. Код, как всегда, доступен на github.