Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.

Алгоритмы нахождения MST применимы в различных областях, начиная от кластеризации данных до построения компьютерных, транспортных сетей.
Я надеюсь, что вы после прочтения данной статьи, примерно понимали, как работают жадные алгоритмы нахождения MST.

Визуализация графов проводится с помощью graphonline.

Формальная постановка задачи

Имеется следующий неориентированный взвешенный граф. Назовем остовным деревом подграф, содержащий все вершины исходного графа, который является деревом. И задача состоит в том, чтобы найти такое остовное дерево, сумма рёбер которого минимальна.

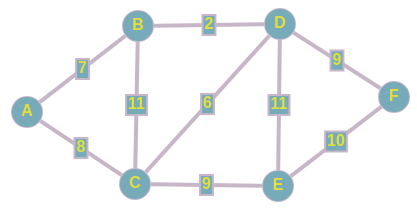
Неформальная постановка задачи

Представьте исходный граф без рёбер, теперь вам нужно как-то соединить все вершины между собой, чтобы можно было бы попасть из любой вершины в другую, не имея при этом циклов в получившемся графе с минимально возможной суммой весов включенных рёбер.

Алгоритм Краскала

Механизм, по которому работает данный алгоритм, очень прост. На входе имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева. Будем рассматривать только связные графы, в другом случае при применении алгоритма Краскала мы будем получать не минимальное остовное дерево, а просто остовной лес.

• Вначале мы производим сортировку рёбер по неубыванию по их весам.

• Добавляем i-ое ребро в наш подграф только в том случае, если данное ребро соединяет две разные компоненты связности, одним из которых является наш подграф. То есть, на каждом шаге добавляется минимальное по весу ребро, один конец которого содержится в нашем подграфе, а другой - еще нет.

• Алгоритм завершит свою работу после того, как множество вершин нашего подграфа совпадет с множеством вершин исходного графа.

Данный алгоритм называется жадным из-за того, что мы на каждом шаге пытаемся найти оптимальный вариант, который приведет к оптимальному решению в целом.

Разбор конкретного примера по шагам

Из представленного сверху графа, выпишем все его ребра в отсортированном порядке:

1) D <--> B; w = 2
2) D <--> C; w = 6
3) A <--> B; w = 7
4) A <--> C; w = 8
5) C <--> E; w = 9
6) D <--> F; w = 9
7) F <--> E; w = 10
8) B <--> C; w = 11
9) D <--> E; w = 11

И начнем по списку добавлять эти ребра в наш остов:

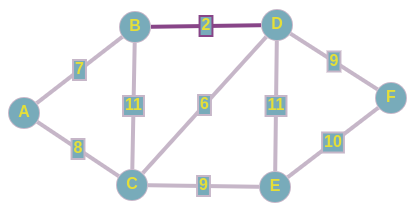
При добавлении в наше остовное дерево ребра A <--> C, как вы можете заметить, образовывается цикл, поэтому мы просто пропускаем данное ребро.

По итогу у нас образовывается следующий подграф, и как вы заметили, мы соединили все вершины ребрами с минимально-возможными весами, а значит, нашли минимальное остовное дерево для нашего исходного графа.

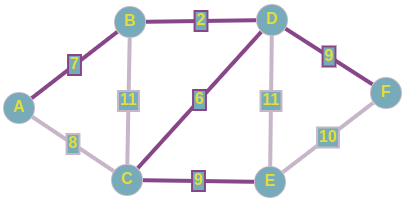
Проводим проверку с помощью встроенного алгоритма для нахождения MST на graphonline, и видим, что подграфы идентичны.
И да, из-за того, что при равенстве весов рёбер мы можем выбрать любое из них, конечные подграфы, являющиеся минимальными остовными деревьями, могут различаться с точностью до некоторых рёбер.

Суммарный вес искомого MST равен 33.

Реализация

Реализовать представленный алгоритм проще всего с помощью СНМ(система непересекающихся отрезков).

Вначале, как мы уже раннее говорили, необходимо отсортировать ребра по неубыванию по их весам. Далее с помощью вызовов функции make_set()мы каждую вершину можем поместить в свое собственное дерево, то есть, создаем некоторое множество подграфов. Дальше итерируемся по всем ребрам в отсортированном порядке и смотрим, принадлежат ли инцидентные вершины текущего ребра разным подграфам с помощью функции find_set() или нет, если оба конца лежат в разных компонентах, то объединяем два разных подграфа в один с помощью функции union_sets().

В итоге асимптотическая сложность данного алгоритма сводится к:

, где:
sort() -
make_set()-
find_set -
union_sets -

vector<int> parent, rank;

void make_set(int v) {
    parent[v] = v;
    rank[v] = 0;
}

int find_set(int v) {
    if (v == parent[v])
        return v;
    return parent[v] = find_set(parent[v]);
}

void union_sets(int a, int b) {
    a = find_set(a);
    b = find_set(b);
    if (a != b) {
        if (rank[a] < rank[b])
            swap(a, b);
        parent[b] = a;
        if (rank[a] == rank[b])
            rank[a]++;
    }
}

struct Edge {
    int u, v, weight;
    bool operator<(Edge const& other) {
        return weight < other.weight;
    }
};

int n;
vector<Edge> edges;

int cost = 0;
vector<Edge> result;
parent.resize(n);
rank.resize(n);
for (int i = 0; i < n; i++)
    make_set(i);

sort(edges.begin(), edges.end());

for (Edge e : edges) {
    if (find_set(e.u) != find_set(e.v)) {
        cost += e.weight;
        result.push_back(e);
        union_sets(e.u, e.v);
    }
}

Алгоритм Прима

Суть самого алгоритма Прима тоже сводится к жадному перебору рёбер, но уже из определенного множества. На входе так же имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева.

• Изначально наш подграф состоит из одной любой вершины исходного графа.

• Затем из рёбер инцидентных этой вершине, выбирается такое минимальное ребро, которое связала бы две абсолютно разные компоненты связности, одной из которых и является наш подграф. То есть, как только у нас появляется возможность добавить новую вершину в наш подграф, мы тут же включаем ее по минимальмально возможному весу.

• Продолжаем выполнять предыдущий шаг до тех пор, пока не найдем искомое MST.

Разбор конкретного примера

Выбираем чисто случайно вершину E,далее рассмотрим все ребра исходящие из нее, включаем в наше остовное дерево ребро C <--> E; w = 9, так как данное ребро имеет минимальный вес из всех рёбер инцидентных множеству вершин нашего подграфа. Имеем следующее:

Теперь выборка производится из рёбер:
D <--> C; w = 6
A <--> C; w = 8
F <--> E; w = 10
B <--> C; w = 11
D <--> E; w = 11

То есть, в данный момент, мы знаем только о двух вершинах, соответственно, знаем о всех ребрах, исходящих из них. Про связи между другими вершинами, которые не включены в наш подграф, мы ничего не знаем, поэтому они на этом шаге не рассматриваются.

Добавляем в наш подграф реброD <--> C и по аналогии добаляем ребро D <--> B. Получаем следующее:

Давайте добьем наш подграф до минимального остовного дерева. Вы, наверное, уже догадались о том, по каким ребрам мы будем связывать наши оставшиеся вершины:
A и F.

Проводим последние штрихи и получили тот же самый подграф в качестве минимального остовного дерева. Но как мы раннее говорили, сам подграф ничего не решает, главное тут - множество рёбер, которые включены в наше остовное дерево.

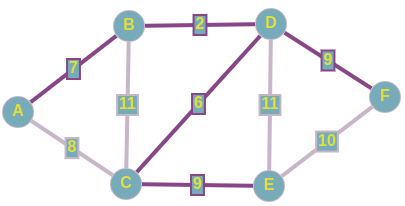
Суммарный вес искомого MST равен 33.

Источники

Инструмент для работы с графами
Лекция Павла Маврина