Заставляем компьютер выводить общие законы физики из наблюдений / forpes.ru

Главная
Заставляем компьютер выводить общие законы физики из наблюдений

Заставляем компьютер выводить общие законы физики из наблюдений +20

02.08.2021 12:47

Tereshkov 18 5800 Источник

Как правило, компьютеры в естественных науках занимаются либо получением чисел из чисел, либо выводом формул из формул. Попытаемся решить более экстравагантную задачу — из набора численных данных вывести формулы общих физических законов, причём не только неизвестные параметры формул, но и сам их вид. В качестве примера рассмотрим задачу о кеплеровых орбитах — в частности, о движении спутника вокруг Земли, и получим законы сохранения энергии и момента импульса, из которых в небесной механике и выводятся эллипсы орбит и законы Кеплера.

Вдохновением для этих занятий послужила замечательная статья из Science, которая убедила меня и многих других в том, что к таким задачам в принципе можно подступиться. Как и у авторов статьи, наш пример будет немного игрушечным, хоть и для совсем другой физической системы. Более того, мы ещё сильнее ограничим пространство поиска (до $2^{64}$ формул, что тоже немало), зато обойдёмся без 32 процессорных ядер и без GPU, а решение получим меньше чем за минуту против десятков минут или даже пары дней, как в статье. Для всего этого нам понадобится лишь 300 строк кода на C — и никаких фреймворков.

Вход и выход

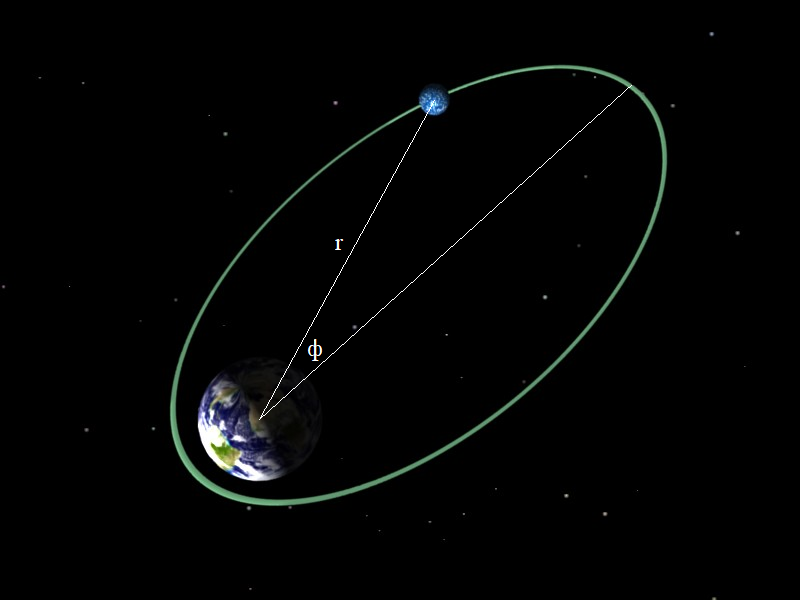
Итак, будем рассматривать движение спутника вокруг Земли, подчиняющееся закону всемирного тяготения $F={GMm}/{r^2}$ , где для удобства возьмём GM=1 и m=1 . Источником измерительных данных будет служить симулятор, выдающий массив полярных координат спутника в плоскости орбиты: расстояний и углов $\phi$ . Для основного алгоритма поиска симулятор является чёрным ящиком, так что никакого закона тяготения алгоритм поиска изначально не знает.

Вопрос о выходных данных сложнее. В ответе требуется иметь не число и не массив чисел, а формулу. Представим её в виде байт-кода простейшей стековой виртуальной машины, которая может оперировать следующими базовыми понятиями:

Действительные переменные
Целые числовые константы от 0 до 5
Сложение, вычитание, умножение, деление
Возведение в квадрат

Система команд виртуальной машины

Код	Мнемоника	Значение
0	0	Загрузка константы 0
...	...	...
5	5	Загрузка константы 5
6	a	Загрузка переменной a
...	...	...
9	d	Загрузка переменной d
10	+	Сложение
11	-	Вычитание
12	*	Умножение
13	/	Деление
14	^	Возведение в квадрат
15	.	Нет операции

Такой ограниченный набор позволяет уместить каждую команду виртуальной машины в 4 бита. Если теперь дополнительно ограничить длину формулы 16 командами, то любая формула будет представима в виде одного 64-битного целого числа. Это сулит исключительные удобства: тип данных uint64_t поддерживается как родной современными процессорами и компиляторами, любая формула целиком помещается в регистр процессора и легко передаётся в функции по значению. По сравнению с подходом авторов статьи в Science, всё это сильно упрощает и ускоряет обработку данных, а в конце концов позволяет быстро получить решение даже на весьма убогой машине.

В качестве четырёх допустимых переменных a, b,c, d у нас будут выступать расстояния и углы $\phi$ , взятые от симулятора, а также скорости их изменения (иными словами, производные по времени) $\dot r$ и $\dot \phi$ . Коль скоро мы взялись искать законы сохранения, то решением для нас будет любая формула, которая при подстановке в неё переменных, соответствующих истинному движению спутника, не будет изменять своего значения вдоль всей его орбиты, как бы ни менялись при этом сами переменные:

$f(r, \phi, \dot r, \dot \phi)=const$

Критерии качества формулы

Условие f=const можно записать и иначе: скорость изменения самой сохраняющейся величины должна быть нулевой, то есть $\dot f=0$ . Разумеется, из-за численных ошибок (а в реальной жизни ещё и из-за ошибок измерения) ни одна найденная нами формула не будет удовлетворять этому условию точно. Следовательно, мы можем лишь пожелать иметь как можно меньшее среднеквадратичное значение $RMS(\dot f)$ , посчитанное вдоль всей орбиты. Тогда для удобства ранжирования формул по качеству можно взять величину $S=-lg(RMS(\dot f))$ . Чем она больше, тем точнее сохраняется найденная величина .

Однако сразу же приходит понимание того, что существует множество формул вроде f = 0 или f=r/r+42 , которые совершенно постоянны и будто бы идеально соответствуют выбранному критерию качества (для них $S=\infty$ ), однако на самом деле тривиальны, поскольку просто не зависят ни от одной переменной. Поэтому необходим дополнительный критерий: у функции должны быть ненулевые составляющие градиента, то есть ненулевая чувствительность к её аргументам. В зависимости от того, к каким именно аргументам (среди четырёх имеющихся) мы потребуем чувствительности, алгоритм будет сходиться к разным сохраняющимся величинам.

Закон сохранения момента импульса

Начнём с очевидного. Потребуем ненулевой чувствительности к и запустим поиск максимума случайным перебором формул (ничего проще и тупее и не придумаешь!). Уже через несколько секунд начнут попадаться формулы вроде da^..*5/........ .

Попробуем расшифровать эту формулу. Воспользуемся мнемониками команд нашей виртуальной машины. Учтём соответствия переменных $a=r, d=\dot \phi$ . Наконец, вспомним о том, что последовательность команд стековой машины фактически содержит формулу вычисляемого выражения в обратной польской записи. Тогда окажется, что компьютер предлагает нам формулу $f=\dot \phi r^2 /5$ . Делитель 5 не играет никакой роли в том, будет ли величина сохраняться или нет, и его можно смело отбросить. Получается, что мы нашли соотношение

$r^2 \dot \phi=const$

Это не что иное, как закон сохранения момента импульса. Момент импульса — это, грубо говоря, произведение импульса тела на плечо . У нас m=1 , $v=r \dot \phi$ , так что закон имеет в точности тот вид, который мы и обнаружили. Можно даже вычислить конкретное значение этой константы. Для той орбиты, которая заложена в симулятор, получается $r^2 \dot \phi=2$ . Итак, у нас есть первый нетривиальный результат. Его наглядной геометрической трактовкой служит второй закон Кеплера:

За равные промежутки времени радиус-вектор спутника заметает равные площади.

Закон сохранения энергии

Закон сохранения энергии найти намного сложнее. Начинать следует с того, чтобы направить поиск в нужное русло, а именно потребовать, чтобы сохраняющаяся величина имела ненулевую чувствительность к скоростям $\dot r$ и $\dot \phi$ . В противном случае алгоритм будет постоянно натыкаться на формулы момента импульса. Их много, они рассеяны по всему пространству поиска, выглядят совершенно по-разному, украшены всевозможными бесполезными множителями и делителями, но физически все выражают один и тот же закон сохранения момента импульса, с которым мы уже разобрались. Теперь эти формулы стали для нас помехой, и найти среди них гораздо более сложные и редкие формулы закона сохранения энергии очень трудно. Когда эта помеха наконец исключена, обнаруживается, что случайный поиск не приносит больше ничего. Разумеется, бессмысленно надеяться и на исчерпывающий перебор среди всех $2^{64}$ формул. Ну а поскольку мы ищем дискретную величину, не даст результата и градиентный спуск.

Однако ничто не мешает применить, например, генетические алгоритмы или имитацию отжига. Наш метод будет похож на имитацию отжига. Создадим начальный набор случайных формул. На каждом шаге "отжига" будем вносить в формулы небольшие случайные модификации (менять одну из 16 команд виртуальной машины). Если критерий качества формулы при этом возрос, то есть S'>S , то модифицированная формула заменяет исходную. Если же он снизился, то модифицированная формула тоже может заменить исходную, но лишь с вероятностью p=exp((S'-S)/T) , где — "температура". Обычно по мере "отжига" уменьшают "температуру", однако даже без этого "охлаждения" удаётся получить результат. Спустя 1000 шагов при размере набора 500 формул часто находится несколько подходящих вариантов (их точное количество и вид зависят от генератора случайных чисел). Например:

.c^d3a-*d5.5++-+
d5.d+da.*-c.^++.

Расшифруем первую формулу (вторая даёт то же самое):

$f=\dot r^2 + \dot \phi (3-r)-(\dot \phi+5+5)=\dot r^2 - \dot \phi(r-2)-10$

После отбрасывания бесполезного члена -10 остаётся странное выражение, как будто бы не похожее ни на один из известных законов сохранения:

$\dot r^2 - \dot \phi(r-2)=const$

Однако можно вспомнить, что раньше мы получили закон сохранения момента импульса в виде $r^2 \dot \phi=2$ . Если теперь подставить этот момент импульса вместо 2, то получим:

$(\dot r^2 + r^2 \dot \phi^2)/2-1/r=const$

А это уже закон сохранения энергии. Первый член представляет собой кинетическую энергию, в которой квадрат скорости выражен в полярных координатах. Второй член -1/r описывает потенциальную энергию гравитационного притяжения, раз уж мы приняли GM=1 . Их сумма, то есть полная энергия, постоянна.

Итак, мы нашли в аналитическом виде два фундаментальных закона сохранения, опираясь лишь на численные данные о координатах движущегося спутника, с чем себя и поздравим.

Код на GitHub

Комментарии (18)

true-grue
02.08.2021 14:00
#23327032
Любопытная заметка! Спасибо Вам за ссылку на статью, послужившую вдохновением. Странно только, что Вы поместили свой текст в "компиляторы", но ни словом не обмолвились, что техника, которую Вы применяете, относится к известному и весьма сегодня популярному направлению -- синтезу программ. Опять же, если обращаться к компиляторным технологиям, хотел бы поинтересоваться, почему в своих решениях Вы не пошли по пути традиционной супероптимизации?
1. Tereshkov Автор
  02.08.2021 14:23
  #23327140
  По правде сказать, я с самого начала (ещё до обнаружения статьи в Science) размышлял над этой задачей преимущественно со стороны физики. Связь с компиляторами мне поначалу показалась поверхностной и чуть ли не случайной. Не поделитесь чем-нибудь интересным и релевантным по теме супероптимизации?
  
  Кстати, сейчас полюбопытствовал и обнаружил, что физики продолжают довольно активно писать об этом предмете, и кажется, безо всякой связи с компиляторами.
  1. true-grue
    02.08.2021 14:32
    #23327186
    Индуктивный синтез программ, в сущности, представляет собой поиск в пространстве возможных программ по заданной спецификации (состоящей из примеров входов и выходов, различного рода ограничений). В супероптимизаторах предпочтение отдается самому короткому решению, поэтому синтез начинают с программы длиной 1, затем 2 и так далее.
    
    Вот, к примеру, уже классическая работа по синтезу линейных RISC-подобных программ: Synthesis of Loop-free Programs.

OBIEESupport
02.08.2021 14:47
#23327278
Спасибо за статью!

Дискуссия, я думаю, будет еще плодотворней, если написать как из обратной польской бесскобочной записи рождаются такие красивые формулы. Статью из архив.орг тоже прочитал, отдельное спасибо. Вроде бы сумасшедшая идея, анализировать траекторию движения динамической системы через AI, но какая она, оказывается, плодотворная!

shadovv76
02.08.2021 15:07
#23327400
+2
трудно понять дает ли это пользу. По сути вы уже знаете что ищете и подправляете условия чтобы получить желаемое.

чем то похоже на написание биржевого робота приносящего максимальную прибыль по историческим данным, путем подбора частных параметров. И как следствие работает он только на этой истории.

как правильно сформулировать УНИВЕРСАЛЬНЫЕ условия, чтобы получить то чего еще не знаешь :) ?

для момента импульса вы откинули -10, а для ЗСЭ двойку заменили моментом импульса. Почему -10 вы не приняли как -5*на момент импульса?
1. Tereshkov Автор
  02.08.2021 15:55
  #23327630
  Не согласен. Разумеется, алгоритм не знает, что такое энергия и момент импульса, поэтому от него нельзя требовать, чтобы он искал именно закон сохранения энергии или момента импульса. Он ищет любые сохраняющиеся величины, не отдавая преимущества ни одной из них, кроме как в силу их встречаемости в пространстве поиска. Интерпретация этих величин - задача человека.
  
  Для установления универсальности сохраняющейся величины можно запустить симулятор несколько раз с разными параметрами и начальными условиями. Тогда и окажется, что -10 в первом случае действительно остаётся неизменным, а 2 во втором случае изменится вместе с моментом импульса.
  
  Если вы хотите найти этим алгоритмом по-настоящему неизвестное, то для начала надо предложить ему такую физическую систему, для которой вы не знаете законов сохранения. Я намеренно взял знакомую систему, чтобы проконтролировать результат.
  1. VMarkelov
    08.08.2021 03:01
    #23347804
    Думаю, что
    
    Начинать следует с того, чтобы направить поиск в нужное русло, а именно потребовать, чтобы сохраняющаяся величина имела ненулевую чувствительность к скоростям и .
    
    как раз выглядит как "подправление условий". В случае действительно незнакомых законов, нет знаний куда надо подправлять.
    
    Tereshkov Автор
    08.08.2021 22:55
    #23349658
    В случае действительно незнакомых законов, нет знаний куда надо подправлять.
    
    Разумеется. Но вариантов "куда подправлять" в рассматриваемой задаче не так уж много: 2 в степени 4 = 16. Если речь идёт о незнакомой (особенно большой) системе, конечно, нужен ручной или полуавтоматический отбор и анализ решений.
    
    И кстати, эта задача трудна даже когда человек-исследователь сам берётся искать законы сохранения: независима ли сохраняющаяся величина от всех предыдущих? случайно ли величина сохраняется или это глубокий закон? В статье в Science цитируются исследования насчёт ошибок, которые люди при этом допускают.
    
    VitalyDeCoder
    15.11.2021 18:07
    #23708511
    Здравствуйте! Я простой строитель, без высшего образования, но в свободное время интересуюсь наукой и пытаюсь, что-то понять.
    
    Вопрос у меня такой: Можете ли Вы написать код для проверки подлинности фундаментальных законов природы?
    
    Вы взяли симулятор, который строит орбиту в соответствии с F=GMm/R² и получили результаты, которые согласуются с ним. Если допустить, что эта формула не верна, то все результаты неверны. Давайте рассмотрим GM=const. Чему равна эта константа? Она равна W²•R³ - константа Кеплера. GM=W²•R³.... Эта константа для Земли=4е14m³/s², Солнца=1,3е20... Видите, масса небесного тела зависит от угловой скорости....что сразу вступает в конфликт с классической механикой Ньютона:
    
    "...Объектом, о котором идёт речь во втором законе Ньютона, является материальная точка, обладающая неотъемлемым свойством — инерцией [4], величина которой характеризуется массой. В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и не зависящей от каких-либо особенностей её движения и взаимодействия с другими телами."
    
    Если мы намагнитим железную болванку, мы никак не повлияем на ее инерциальную массу или её вес. Но теперь эта болванка будет влиять на другие железяки, примерно так- W²•R³, до намагничивания болванка никак не влияла...очевидно, W²•R³ это параметры сохраненной энергии, что получила болванка из внешнего источника и не зависит от массы болванки а только от свойств вещества из которого она состоит.
    
    Я конечно могу ошибаться, в силу необразованности своей, но я очень четко и ясно формулирую свои подозрения не прибегая к сложным формулам и софистике.
    
    Я думаю что Масса прописана прямо в первой строке кода этой вселенной, но полностью не уверен в этом...
    
    В виду тупости своей, у меня так же есть вопросы к Третьему закону Кеплера:
    
    Третий закон Кеплера описан в книге "Гармония мира" в одном абзаце, начинается на странице 189 и заканчивается на 190. Эта книга о музыке...музыке сфер.
    
    Страница 189 была сфальсифицирована и описание закона полностью утрачено, вероятно фальсификаторы добавили дату:"... 8 марта этого года одна тысяча шестьсот восемнадцать..." В 18 веке одну тысячу лет добавляли и на картинах... Слово "sesquialtera" - полтора, там шла речь о степени 3 и 2, фальсификатор прочитал как 3/2...=1,5 так и написал - полтора. На странице 190 приводится пример, который позволяет восстановить смысл закона: "...Итак, если кто-нибудь возьмет период, скажем, Земли, который составляет один год, и период Сатурна, который составляет тридцать лет, и извлечет кубические корни из этого отношения, а затем возведет в квадрат полученное отношение, возведя в квадрат кубические корни , он будет иметь в качестве своих числовых произведений наиболее справедливое соотношение расстояний Земли и Сатурна от Солнца. 1 Ибо кубический корень из 1 равен 1, а его квадрат равен 1; а кубический корень из 30 больше 3, и, следовательно, его квадрат больше 9. А Сатурн на своем среднем расстоянии от Солнца немного выше, чем в девять раз больше среднего расстояния Земли от Земли. солнце. Далее, в главе 9, использование этой теоремы будет необходимо для демонстрации эксцентриситетов." Старый перевод; https://www.sacred-texts.com/astro/how/how04.htm
    
    Кеплер говорит о среднеарифметическом радиусе эллипса. Мы же говорим о большой полуоси, что совсем не одно и тоже что и средний арифметический радиус.... Мы умнее Кеплера или мы делаем что-то не так? Где правда?
    
    Дисклаймер: Ребята, простите меня... накипело.
    
    Tereshkov Автор
    15.11.2021 19:54
    #23708851
    Можете ли Вы написать код для проверки подлинности фундаментальных законов природы?
    
    Нет. Численным моделированием можно проверить только корректность математических выкладок, но не справедливость закона как такового. Если в модель заложены неверные предпосылки, то получатся и неверные следствия. Моделированием можно, например, подтвердить, что из законов Ньютона следуют законы Кеплера, но это ничего не скажет нам о справедливости самих законов Ньютона.
    
    масса небесного тела зависит от угловой скорости....что сразу вступает в конфликт с классической механикой Ньютона
    
    Это неверно. Во-первых, не угловая скорость, а скорость изменения полярного угла. У материальной точки угловой скорости нет вовсе. У реальной планеты (тела конечных размеров) она есть, но не равна скорости изменения полярного угла из-за суточного вращения. Во-вторых, не масса зависит от этой скорости, а наоборот. Законы Ньютона первичны, а законы Кеплера - лишь их наблюдаемые следствия.
    
    Страница 189 была сфальсифицирована и описание закона полностью утрачено, вероятно фальсификаторы добавили дату:"... 8 марта этого года одна тысяча шестьсот восемнадцать..." В 18 веке одну тысячу лет добавляли и на картинах... Слово "sesquialtera" - полтора, там шла речь о степени 3 и 2, фальсификатор прочитал как 3/2...=1,5 так и написал - полтора.
    
    Чтобы судить о справедливости законов, стоит не читать древние трактаты, а проверять эти законы с карандашом, бумагой, компьютером и телескопом.
    
    VitalyDeCoder
    17.11.2021 22:25
    #23717177
    Я очень рад, что Вы ответили ! Я вообще-то за теорию симуляции. Вижу Вы по диагонали прочитали мой коммент, но это не важно. Средний радиус численно равен большой полуоси, но заменяя его в законе теряется смысловая связь, как заявление что 2π это круг, вроде все верно, при условии что R=1... На примере: В начале поста эллипсная орбита. Если мы знаем, что большая полуось это средний радиус , мы легко можем догадаться, что можем узнать орбитальную скорость в любой точке эллипса, если знаем первую космическую к примеру. V₁²/V₂² = R₂/R₁ Я говорю о передаче знаний ...
    
    Tereshkov Автор
    15.11.2021 23:08
    #23709327
    Чтобы не быть голословным и заодно уберечь вас от псевдонауки, предлагаю вам код численного моделирования, которое как раз и демонстрирует справедливость третьего закона Кеплера (в предположении справедливости второго закона Ньютона и закона всемирного тяготения). Можете сами поварьировать в нём начальные условия для планет и убедиться, что получите для всех одно и то же отношение куба большой полуоси к квадрату периода (варьируйте осторожно, чтобы не получить гиперболическую траекторию). Надеюсь, это избавит и вас, и нас от россказней про "фальсификации" и т.п.
    
    VitalyDeCoder
    17.11.2021 22:44
    #23717261
    Я не знаю с какой стороны подступиться к этому моделированию.... Я с программированием никак. Я заинтересован в сотрудничестве. Запустить копию симуляции на природных законах. Для начала солнечной системы... Код будет работать если заменить GM=V²•R выразить через орбитальную скорость?
    
    Tereshkov Автор
    17.11.2021 23:24
    #23717389
    В начале поста эллипсная орбита. Если мы знаем, что большая полуось это средний радиус , мы легко можем догадаться, что можем узнать орбитальную скорость в любой точке эллипса, если знаем первую космическую к примеру.
    
    Код будет работать если заменить GM=V²•R выразить через орбитальную скорость?
    
    Я понятия не имею, что вы называете "средним радиусом" эллипса. Такого понятия нет. Что за V? Что за R? Что останется от вашего равенства, когда сила не перпендикулярна скорости (а на эллипсе такое будет непременно)? У меня ощущение, что вы пытаетесь за уши притащить сюда какую-то аналогию с круговой орбитой из школьного учебника. Тщетное занятие.
    
    Запустить копию симуляции на природных законах. Для начала солнечной системы...
    
    Тогда собирайте измерительные данные сами, как Тихо Браге, или берите готовые данные от какой-нибудь обсерватории, подставляйте их вместо симулятора и проверяйте хоть законы Кеплера, хоть законы Ньютона.
    
    VitalyDeCoder
    18.11.2021 16:29
    #23720555
    V²•R это энергия это постоянная величина небесного тела. Это та энергия что притягивает тела. В симуляторах эта энергия вбивается как MG, закрывая возможность ввести массу отдельно. Аналогично как если бы магниты силой 1 ньютон весил 1кг, 2ньютона = 2кг Вот чего я хочу , возможность ввести отдельно 1ньютон и отдельно 1кг или 2 кг сколько я захочу.
    
    Tereshkov Автор
    18.11.2021 21:36
    #23721751
    V²•R это энергия это постоянная величина небесного тела.
    
    Полная нелепость. Поскольку вы не дали определения ни V, ни R, то ваше утверждение бессмысленно. Если вы скажете, что V - это модуль скорости, а R - длина радиус-вектора, то оно превратится из бессмысленного в неверное.
    
    Энергия (в расчёте на единицу массы) равна V²/2 - GM/R, и именно эта величина и сохраняется. Ваша же величина V²R не только не постоянна вдоль эллиптической орбиты (в чём вы можете легко удостовериться из того же численного моделирования), но даже по размерности не совпадает с энергией.
    
    Могу только гадать, откуда вы её взяли, и свою догадку уже высказывал: из школьной формулы для круговой орбиты V²R = GM. В таком случае не забывайте, что, во-первых, это не энергия и она не обязана сохраняться, а во-вторых, эта формула неприменима к эллипсу, гиперболе и вообще хоть чему-нибудь кроме окружности.
    
    VitalyDeCoder
    19.11.2021 19:17
    #23725709
    Ок.Спасибо.