и точно. Точнее, с заданной точностью, простите за каламбур.
Под катом я расскажу, как сделать это с использованием школьного курса алгебры и целочисленной арифметики, при чём здесь полиномы Чебышёва I-го рода, и дам ссылки на примеры реализаций для ПК и Cortex-M3.
Если вам лень вникать в теорию, и нужны только примеры реализации - сразу переходите в конец статьи.
Поехали.
Если нужно найти синус, или другую тригонометрическую функцию на ПК, это делается просто - сейчас в процессоры семейства x86/x64 встроен FPU, а он знает инструкцию fsin, при помощи которой вычисляется искомое. Вычисляется, если говорить с натяжкой, быстро.
Если это надо сделать это на МК без плавающей точки - то возникают проблемы. Можно использовать функцию из поставляемой вместе с компилятором библиотеки, будет точно, но очень медленно. Если надо быстрее - то первое, что приходит в голову, заранее посчитать таблицу со значениями, но точность при этом сильно упадёт, и будет зависеть от шага аргумента между смежными значениями. Следующий интуитивно понятный шаг - использовать интерполяцию по двум соседним точкам таблицы. Это поможет поднять точность, но несильно. Иногда для достижения нужной точности размер таблицы всё равно превосходит разумные пределы.
Что же тогда делать? Увеличивать степень аппроксимации. Это позволит увеличить точность вычислений и (или) уменьшить размер таблиц. И сделать это совсем несложно.
Аппроксимация полиномами
Кусочно-линейная аппроксимация - это, по сути, аппроксимация полиномом первой степени. Выходное значение вычисляется по формуле y = A1·x + A0, где x - это входной аргумент, A0, A1 - некие коэффициенты.
Для примера разобьём весь период от 0 до 2π на 8 равных интервалов, и для каждого подберём такие коэффициенты A0 и A1, что бы максимум ошибки при любом аргументе был минимален (как это сделать, я расскажу ниже). Если мы построим график этого "синуса", он будет выглядеть примерно так (сплошная линия):

Штриховой линией нарисовано более точное значение синуса. А график ошибки (разницы между "настоящим" и аппроксимированным значениями будет таким:

На нём, если приглядеться, не выполняется условие "максимум ошибки при любом аргументе был минимален", но сейчас это неважно. Максимальная ошибка составляет 0.03684497.
Небольшое отступление. Числа вроде 0.03684497 или 2.448728e-09 слишком абстрактны для понимания, их трудно сравнивать. Мне, как человеку, долгое время работающему в двоичной системе, гораздо ближе биты. Поэтому к ним я и буду приводить величину ошибки, беря от неё минус логарифм по основанию 2, тогда она превращаются соответственно в 4.76 или 28.6 бит. По мне, такие логарифмические "попугаи" проще для восприятия и нагляднее. По итогам предыдущего абзаца можно сказать, что "значение синуса вычислено с точностью 4.76239 бита".
Теперь давайте разобьём один период (от 0 до 2π) не на 8, а на 64 интервала, по 16 на каждый квадрант. И рассмотрим один интервал в районе, например, 45°. График ошибки (сплошная чёрная линия) выглядит так:

Он очень похож на график параболы y = x², который нарисован там же красным штрих-пунктиром. Так же, как парабола, выглядит график полинома Чебышёва I-рода 2-й степени (более того, он ей и является). На КДПВ, он изображён голубой линией.
А что если мы учтём это, и попробуем на этом же отрезке вычислять синус по формуле y = A2·x² + A1·x + A0?
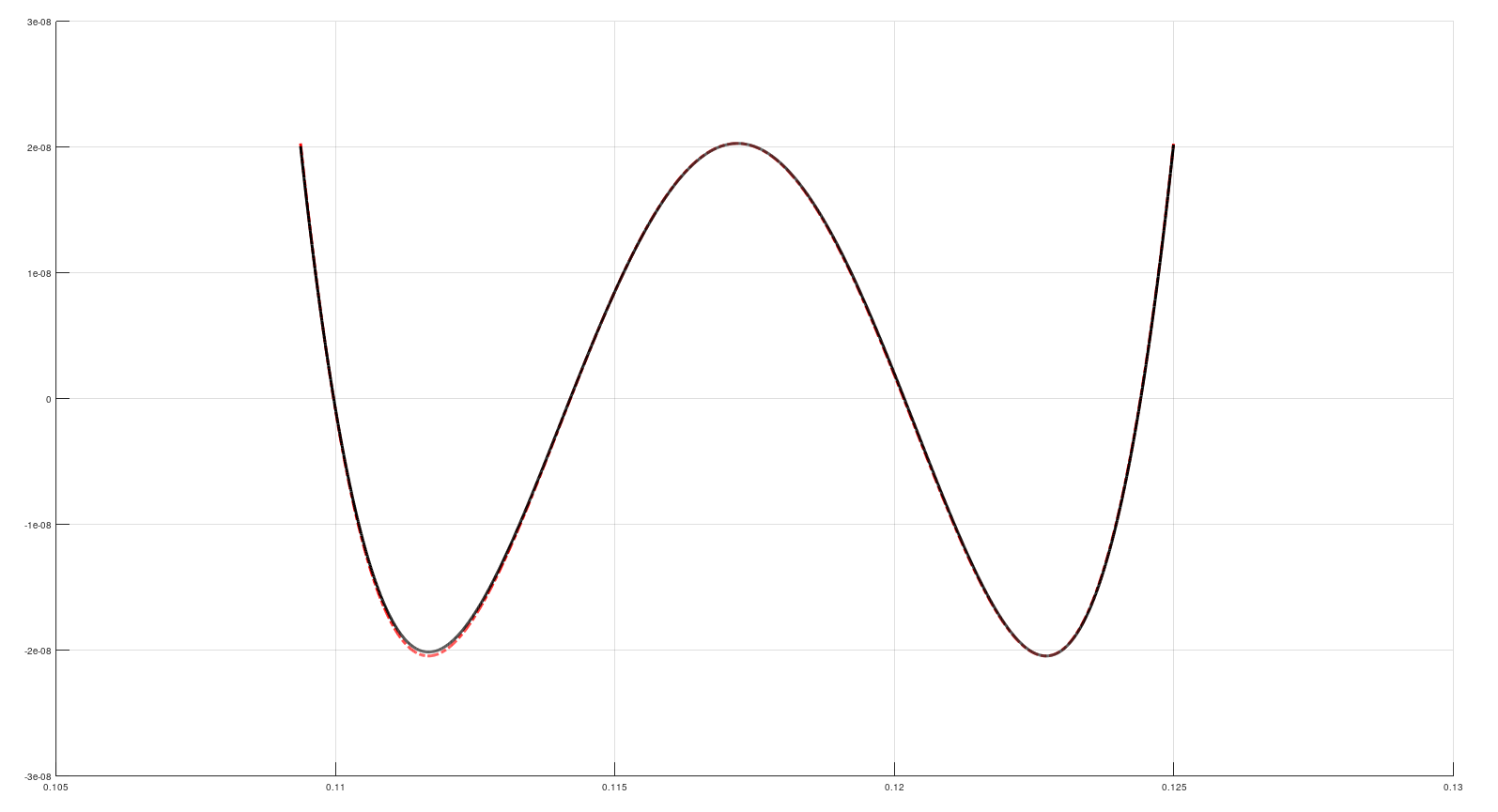
Считаем тройку коэффициентов А0, А1, А2 (как - об этом ниже), по ним считаем целевой синус, и находим ошибку (сплошная чёрная линия):

Красным штрих-пунктиром нарисован полином Чебышёва3-й степени, и снова оба графика очень похожи.
Здесь я открою маленький секрет. График синуса, найденный аппроксимацией функцией 2-степени по 8 интервалам, с точностью до долей пикселя совпадает с "настоящим", и, будучи нарисованными вместе, они полностью перекрывали бы друг друга. Тремя картинками выше, где нарисованы графики, сиреневым пунктиром изображён не "настоящий" синус, а полученный функцией 2-й степени.
Как сильно увеличилась точность при переходе от 1-й ко 2-й степени? Для 64 интервалов на период она возросла с 10.7 до 17.63 бит. Откуда взялись эти числа, я расскажу ниже.
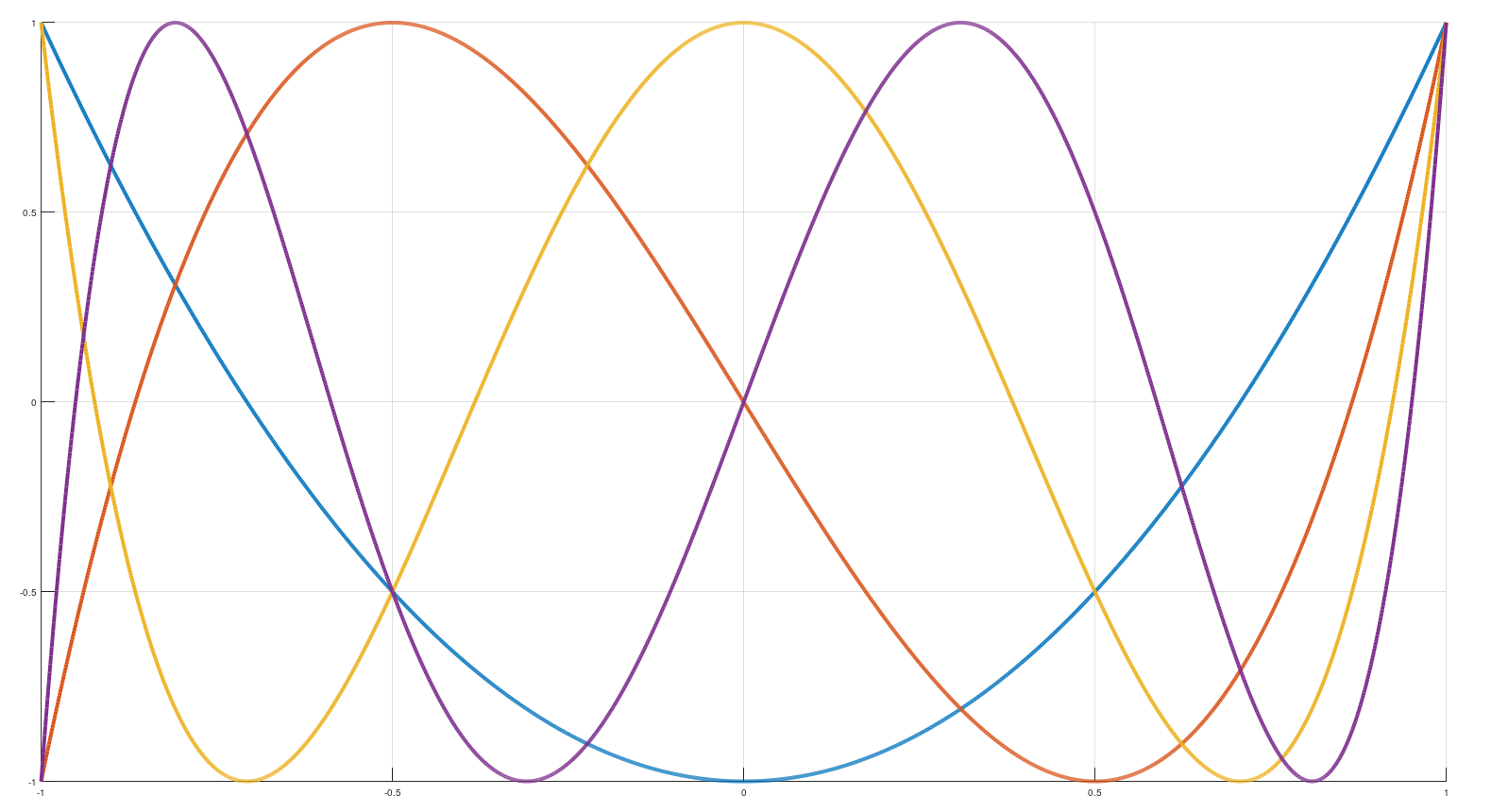
Если мы дальше продолжим увеличивать степень полинома, то ошибки будут ещё меньше, и будут приобретать формы полиномов Чебышёва разных степеней:

Точность аппроксимации на 64 отрезках при этом возрастёт до 24.980 бит (3-я степень) и 32.651 бит (4-я степень).
Если дальше повышать степень - тенденции сохранятся. Думаю, смысл применения полиномов для аппроксимации синуса понятен.
Как считать коэффициенты
В википедии, в статье про полиномы Чебышёва есть фраза: "Многочлены Чебышёва играют важную роль в теории приближений, поскольку корни многочленов Чебышёва первого рода используются в качестве узлов в интерполяции алгебраическими многочленами". Это как раз наш случай.
Посмотрим ещё раз на их графики:

Голубая линия (полином 2-й степени) пересекает ось абсцисс (y=0) в двух точках x = ±0.7071. Оранжевая (3-й степени) - в трёх точках: x = 0 и x = ±0.866. Это и есть корни полиномов, они будут использованы "в качестве узлов в интерполяции".
Ещё небольшое отступление, как представлять аргументы. На 32-битных процессорах полный период (круг) удобно представить как 232 (0x100000000), а угол, соответственно, в диапазоне от 0 до 0xffffffff. Если количество интервалов аппроксимации, на которые разбит круг, равно 2n, то угол можно интерпретировать как двоичное число с фиксированной точкой. Например, при разбиении на 64 интервала (26), угол будет интерпретироваться как число размерности 6.26. Здесь старшие 6 бит - это номер интервала (считая от нуля), а младшие 26 бит - смещение внутри него.
Возьмём, для примера, угол 15°. Если вычислить 15°/360° · 232, то получим 0000_1010_1010_1010_1010_1010_1010_1011 в двоичном виде. В размерности 6.26 будет выглядеть как 000010.10101010101010101010101011. Здесь первые 6 бит 000010 - это десятичное 2 (2-й интервал), а оставшиеся 26 10101010101010101010101011, будучи поделены на 226, дадут 0.66666667 - это смещение внутри интервала. То же самое получим: 2.66666667 = 64 * 15/360.
Смещение внутри интервала лежит в диапазоне 0.0 ≤ x < 1.0. К нему же надо привести корни многочленов Чебышёва, которые находятся между -1 и +1. Корни полинома 2-й степени превратятся 0.14645 и 0.85355, 3-й степени - 0.066987, 0.5 и 0.933013.
Теперь давайте найдём коэффициенты A0, A1 и т.д. При аппроксимации полиномом 1-й степени y = A1·x + A0 нам нужно, что бы на заданном интервале с номером N в точке со смещением 0.14645 целевое значение было равно y=sin((N + 0.14645)/64 * 2π), а в точке 0.85355 - y=sin((N + 0.85355)/64 * 2π). Это делается при помощи системы из двух линейных уравнений с 2 неизвестными A1 и A0:
A1·0.14645 + A0 = sin((N + 0.14645)/64 * 2π)
A1·0.85355 + A0 = sin((N + 0.85355)/64 * 2π)
Для интервала N=2 (где находится 15°), получаем: A1 = 0.09521 и A0 = 0.19523.
Пройдясь по всем N, от 0 до 63, получим таблицу с наборами коэффициентов A1 и A0. С ней уже можно считать синус с точностью 10.7 бит. Как это делать, расскажу ниже (если кто до сих пор не понял сам).
Перейдём ко 2-й степени y = A2·x² + A1·x + A0. В качестве аргумента x подставим, соответственно, корни полинома 3-й степени 0.066987, 0.5 и 0.933013. Напишем систему из 3 уравнений с 3 неизвестными A2, A1 и A0:
A2·0.066987² + A1·0.066987 + A0 = sin((N + 0.066987)/64 * 2π)
A2·0.5² + A1·0.5 + A0 = sin((N + 0.5)/64 * 2π)
A2·0.933013² + A1·0.933013 + A0 = sin((N + 0.933013)/64 * 2π)
Решения для интервала N=15 будут следующие:
A2 = -0.004812613
A1 = +0.009628370
A0 = +0.995184425
Обратите внимание на A2 и A1. Если их умножить 27 и 26 соответственно, то их значения всё равно будет лежать в пределах от -1 до +1. Интервал №15 я выбрал не случайно - на нём значение A0 максимально и близко к 1.
Вообще, в большинстве случаев коэффициенты при больших степенях можно увеличить на некий коэффициент. При целочисленных операциях это уменьшит погрешность вычислений, а на Cortex-M3 к тому же сократит их время - об этом я расскажу ниже.
Для вычисления таблиц других размеров в предыдущую систему уравнений вместо 64 нужно подставить нужный размер. Для аппроксимации полиномом степени P нужно найти корни полинома Чебышёва степени P+1, и записать систему из P+1 уравнений с P+1 неизвестными, не забывая возводить корень многочлена в нужную степень 'n' при каждом An. (Если предыдущее предложение непонятно, то ничего страшного. Ближе к концу статьи будет ссылка на готовый генератор таблиц и краткая инструкция к нему.)
Точность вычислений
Разные комбинации размера таблицы и степени полинома дают разную погрешность. Не имея представления, как определить её аналитически, я решил считать "в лоб", перебирая все возможные комбинации, и прогоняя через каждую все углы от 0 до 0xffffffff. Для этого был создан проект accuracy_test. Суть в следующем:
в проект включены таблицы, степенью полинома от 1 до 6 и размером от 4 до 65536, всего 90 штук. Какие таблицы проверяем, указывается в аргументах при запуске. Можно указать набор или диапазон проверяемых таблиц;
с помощью заданной таблицы производится аппроксимация синуса по всем возможным 4294967296 аргументам. Результат аппроксимации сравнивается со значением, полученным стандартной функцией sinl(), получается разница-ошибка;
находится самая большая в абсолютном значении ошибка - это самый худший случай аппроксимации. Можно утверждать, что заданным методом точность вычисления не хуже, чем эта самая ошибка.
Количество аргументов от 0 до 232-1 велико, но не бесконечно, и их перебор занимает какое-то конечное время. Ноутбук с Intel Core-I7 перебирает их примерно за 6, а одноплатный компьютер на Allwinner A20 за 25 минут. Причём на ПК, как показал один эксперимент, львиную часть времени занимает вычисление "эталонного" значения функцией sinl.
Результаты проверок всех 90 таблиц в конечном итоге сводятся в одну небольшую табличку, на основании которой строится диаграмма:

На ней видно, что с увеличением размера таблицы точность растёт, и тем быстрее, чем выше степень полинома, при этом не поднимаясь выше 54 бит. Это самая большая точность, которую мне удалось достичь, при этом вычисления производились на ПК, с помощью 80-битных чисел с плавающей точкой (long double). Почему я заострил внимание "на ПК", будет чуть дальше.
При использовании 32-битных целочисленных вычислений результаты скромнее:

Здесь точность не превышает 30.36 бит. Но с учётом того, что старший бит отведён под знак числа, ошибка получается менее самого младшего бита.
На этой диаграмме, как видно, присутствуютне все комбинации размера таблицы и степени полинома. Это связано с тем, что некоторые коэффициенты при малом количестве интервалов превышают 1, и при умножении на 0x7f000000 выходят за пределы знакового 32-битного числа. Компилятор предупреждает об этом, а попытки определить точность дают результат в районе 0 бит.
Максимальная точность на 32-битных целых числах, которую я получил, составляет 30.37 бит при множителе 0x7fffff00.
Несколько слов о вычислениях на ARM со встроенным АРМовским FPU (armhf)
Результаты неприятно удивили.
Во-первых, выяснилось, что он может работать только с 64-битными числами с плавющей точкой (в отличии от 80-битных long double на x86/x64), и нет разницы, переменные какого типа пытаться использовать - double или long double, компилятор всё сводит к double.
Во-вторых, вычисления на ARM по точности немного отличаются от таких на x86 в худшую сторону - при долгой работе с числами набегают ошибки округления. Это можно увидеть, если посмотреть на соответствующие диаграммы для 64-битных float (файл формата ods, xls). ARM хуже вычисляет как и сами таблицы, так и аппроксимацию синуса на их основе. Причём худший вариант - когда он вычисляет на таблицах, созданных им же. Использование таблиц от x86 дают немного лучший результат, значит таблицы лучше не создавать на ARMах.
Результаты всех проверок сведены в несколько файлов, в каждом из них есть несколько листов:
- для чисел с плавающей точкой - ods, xls;
- для целых 32-битных чисел - ods, xls;
- для чисел с плавающей точкой (ods, xls), когда в качестве эталона использована не sinl, а аппроксимация теми же таблицами.
О последнем надо сказать особо.
Сравним числа с плавающей точкой и какие точности на них достигнуты:
- float 32-бит, мантисса 23+1 бит, точность аппроксимации - 24 бита.
- float 64-бит, мантисса 52+1 бит, точность аппроксимации - 53 бита.
- float 80-бит, мантисса 63+1 бит, точность аппроксимации - почти 54 бита, хотя можно было ожидать 64.
Куда делись 10 бит?
Возникло предположение, что неточно вычисляется "эталонный" синус функцией sinl. Для проверки был проведён эксперимент, где сравнивались результаты аппроксимации двумя разными таблицами. В качестве эталона использовались несколько таблиц длиной 215, 216, разных степеней полинома, а сами вычисления производились 80-битными long double.
Предположение не подтвердилось, зато было замечено, что время проверки уменьшилось в несколько раз! Проверка таблицы 65536_p^1 функцией sinl заняла 279с, а аппроксимацией - 56с. Получается, что более 80% времени процессор был занят вычислением функции sinl.
В свете этого можно рекомендовать использовать на ПК аппроксимацию вместо sinl, можно получить выигрыш во времени.
А куда же делись 10 бит, я так и не понял. Есть подозрение, что точность, равная разрядности мантиссы на 32- и 64-битных float получалась за счёт запаса 80-битных вычислений, результаты которых потом огрублялись до заданных 32 и 64, а без огрубления она как раз составляла те самые 54 бита. При вычислениях на ARMах с 64-битным FPU точность вычисления упала до 50.8 бита против 53 на x86/x64.
Таблицы с коэффициентами
Их можно получить программой make_table. Там есть файл проекта на code::blocks, исходные тексты + скрипт для самостоятельной сборки с помощью gcc, а так же готовый .exe.
В качестве аргументов программа принимает:
- размер таблицы, равный 2n;
- степень полинома;
- множитель для коэффициентов для приведения их к целочисленным значениям;
- параметр AC_SHIFT, показывающий, на сколько бит множитель при коэффициенте, например, 3-й степени будет "весомее" множителя предыдущей 2-й.
Результатом работы программы является исходный код на языке С. Программа выводит его непосредственно на экран, и его можно перенаправить в файл.
Например:
.\make_table.exe 64 3 0x40000000LL 3 > ..\tables\sine_approx_64_3_3.c
создаст файл sine_approx_64_3_3.c. Этот файл содержит таблицу коэффициентов для аппроксимации полиномами 3-й степени по 64 отрезкам, чего достаточно для получения 25-битной точности. Множитель при коэффициенте A0 = 0x40000000, а множители при коэффициентах более высоких степеней будут отличаться от соседних в 2³ = 8 раз.
В начале файла есть набор директив препроцессора, с помощью которых можно настраивать некоторые параметры таблицы:
TABLE_TYPE - тип данных таблицы, по умолчанию int32_t. Его можно "перебить", указав компилятору другой.
Q1_ONLY - указание использовать только первый квадрант, позволяет уменьшить объём таблицы в 4 раза.
DC - "добавка" к ко всем коэффициентам перед превращением их в целочисленный вид, позволяет делать арифметическое округление. По умолчанию равно 0.5 (для int32_t), для чисел с плавающей точной следует задать его равным 0.
AC0 - множитель для коэффициента 0-й степени, по умолчанию 0x40000000LL. Может быть задан другой, для таблицы типа float можно задать 1.
AC_SHIFT - на сколько бит будет сдвинут влево множитель AC0 для каждой последующей степени (механизм этого понятен при формировании множителей AC1, AC2 и так далее). Для таблицы длиной 64 строки оптимальное значение 3, для таблиц другой длины оптимальные значения лежат в районе от 1 до 5.
Каждая строка полученной таблицы выглядит примерно так:
-0.00015749713825 * AC3 + DC, -0.000000170942 * AC2 + DC, +0.098174807817 * AC1 + DC, -0.000000001187 * AC0 + DC, // 0
где
-0.00015749713825096520473455514 * AC3 - коэффициент для x³, -0.00000017094269773828251637917 * AC2 - для x², и так далее.
В конце файла, после таблицы, сформирован отчёт, какой "запас по битам" имеется у каждого коэффициента. В процессе расчёта множителей находятся таковые с максимальными абсолютными значениями. В таблице из примера для множителя 0 степени это 0.999999969786949, что почти рано 1.0, и запаса по битам нет. А максимальный коэффициент 3-го порядка равен 0.00015749713825, его можно безболезненно умножить на 212, и результат будет всё ещё меньше 1. С помощью запаса по битам при желании можно скорректировать сомножители AC1 ... ACn.
Если есть желание повторить проверки точности, то в папке проекта есть скрипт на lua, который может сформировать необходимые исходные файлы, и сформирует cmd-файл, запустив который получится 90 файлов с таблицами на 22 ... 216 строк и степенями от 1 до 6. Впрочем, все они и так присутствуют
Как это использовать на практике
Для использования аппроксимации в своём проекте для начала нужно определиться, с какой точностью нужно вычислять синус. Потом нужно оценить ресурсы (объём памяти и быстродействие вычислителя), которые у вас есть.
К примеру, вы хотите, используя 32-битные целочисленные операции, сделать генератор с 24-битным ЦАП. Старший бит отведён на знак, поэтому точность аппроксимации должна быть не меньше 23 бит. На диаграмме видно, что заданная точность достигается при использовании:
- таблицы на 8192 строки при использовании аппроксимации 1-й степени,
- 512 строк при 2-й степени,
- 64 строки при 3-й степени,
- 32 при 4-й степени,
- 16 при 5-й степени, и
- 8 при 6-й степени.
При желании степень полинома можно увеличить ещё, длина таблицы при этом уменьшится.
Теперь следует определиться с ресурсами и приоритетами их использования. Если вы хотите получить максимальное быстродействие, нужно использовать аппроксимацию 1-й степени, при этом таблица на 8192 строки займёт 64к. Если вы используете какой-нибудь STM32 на Cortex-M3, то размещение таблицы в ОЗУ уменьшит время вычисления в отличии от размещения её в памяти программ, и у ST можно найти контроллеры с объёмом ОЗУ больше 64к.
Если у вас очень мало памяти и есть запас по быстродействию (FPGA например) , можно использовать аппроксимацию с высокими степенями.
Таблицы 5-й и 6-й степеней займут, соответственно, 16 * (5+1) * 4 = 384 и 8 * (6+1) * 4 = 224 байт.
Уменьшить объём ещё в 4 раза можно, используя симметричность функции синуса. Точность при этом может упасть, т.к. при аргументе функции 0x40000000, что равно 90°, будет использован 0x3fffffff, вместо0x40000001 - 0x3ffffffe, и т.д. Для использования этого фокуса, при сборке проекта в опциях компилятора нужно добавить Q1_ONLY - это уменьшит размер таблицы и добавит лишние вычисления в функции get_sine_int32() и get_sine_float().
Примеры использования
Есть 2 готовых примера - для ПК и для популярного STM32F103C8.
Что бы избавиться от лишних умножений для возведения в степень, формула y = A2·x² + A1·x + A0
преобразована к виду y = ((0 + A2)·x + A1)·x + A0
В упрощённом виде код выглядит так:
// angle - угол (доля полного периода в диапазоне от 0.0 до 1.0, фикс.точка 0.32)
// pN - двоичная степень количества интервалов; N = 2^pN
// ac_shift - двоичная степень отношения "весов" смежных коэффициентов
// pw - степень полинома
// table - таблица коэффициентов, одномерный массив размером 2^pN * (pw + 1)
int idx = angle >> (32 - pN); // индекс строки в таблице
uint32_t X = (angle << pN); // X = дробная часть угла * 2^32 (фикс. точка 0.32)
X >>= ac_shift; // уменьшая X, корректируем "веса" коэффициентов
const int32_t* A = table + idx * (pw + 1); // указатель на первый коэфф (при степени pw) в строке таблицы
int64_t sum = A[0];
for(int i = 1; i <= pw; i++)
{
sum *= (int32_t)X; // sum - промежуточный результат, фикс. точ. размерности 32.32
sum >>= 32; // приводим sum к размерности 64.0
sum += A[i]; // прибавляем очередной коэфф.
}
// теперь sum содержит искомое значение
ПК
Там есть 2 функции на выбор - для целочисленных вычислений get_sine_int32 и для вычисления с плавающей точкой get_sine_float. Каждая оформлена в отдельной паре файлов (.h / .c), которые нужно включить в свой проект. Так же в проект надо включить нужную таблицу с коэффициентами. Использование таблиц и функций с плавающей точкой на ПК оправдано, т.к. это позволяет ускорить вычисления.
Cortex-M3
Проект на embitz для STM32F103C8.
Вычисления синуса полиномами от 1-й до 6-й степеней оформлены в виде ассемблерных вставок в код на С. Перед каждой вставкой в комментариях есть примерно измеренное кол-во тактов на 1 цикл вычислений, когда таблица находится во flash и когда в RAM, время получается разное. Размешение таблиц в оперативной памяти позволяет немного поднять быстродействие.
Я не считаю себя знатоком ARMовского ассемблера, возможно кому-то удасться вычисления ускорить.
Здесь надо рассказать о том, почему использование коэффициента AC_SHIFT ускоряет вычисление. У Cortex-M3 есть инструкции умножения двух 32-битных чисел с получением 64-битного результата: UMULL и SMULL. Первая умножает два беззнаковых числа, и нам не подходит, потому коэффициенты есть положительные и отрицательные. Вторая, которую мы используем, умножает знаковые числа:
одно из них - это коэффициент из таблицы, знаковое число,
второе - это смещение угла внутри интервала, число беззнаковое.
Если второе число превысит 0x7fffffff, то оно блоком умножения будет интерпретировано как отрицательное и результат будет не тот, который мы ожидаем. Но инструкции, которая перемножала бы знаковое и беззнаковое число, в наборе команд нет. Мы будем использовать SMULL и позаботимся о том, что бы второе число не превышало 0x7fffffff, уменьшив его минимум в 2 раза. При этом надо будет после каждого умножения корректировать результат. Сделать это можно двумя способами:
- каждый раз удваивать результат, на что уйдут машинные такты;
- сделать в два раза больше то число, которое на него умножаем.
Более экономичным является второй способ. Если x уменьшен в 2 раза, то из формулы y = (((0 + A3)·x + A2)·x + A1)·x + A0
понятно, что в 2 раза должен быть увеличен коэффициент A1, в 4 раза A2, и в 8 раз A3.
Если же x уменьшен в 4 раза, то множители становятся соответственно 4, 16 и 64. За это при компиляции таблиц отвечает параметр AC_SHIFT. Кроме того, его использование убивает второго зайца - коэффициенты, содержащие много нулей после запятой - а они относятся к высоким степеням полиномов, не так сильно теряют точность при округлении.
Вот и всё. Буду рад вашим замечаниям, уточнениям и предложениям.
Комментарии (52)

DrSmile
10.09.2021 13:10+1Размеры таблиц можно уменьшить в (степень полинома + 1) раз ценой большего количества операций используя сплайны вместо полиномов. Т. е. вместо пачки независимых коэффициентов на каждый интервал можно использовать набор последовательных точек из соседних интервалов.

belch84
10.09.2021 14:17Не очень давно мне довелось поспорить на Хабре с одним пользователем. Среди прочего, он уверял, что в серьезных математических пакетах значения полиномов Чебышева вычисляются как Tn(x) = cos(n*arccos(x)). Вышеупомянутый пользователь считает эту формулу удобной и универсальной, ибо она позволяет вычислять значения полиномов Чебышева даже вне их естественного интервала определения [-1,1] (за счет использования комплексных значений arccos(x), где |x|>1). Я не специалист по математическим пакетам, но мне показалось странным, что значения полиномов считаются с помощью прямых и обратных тригонометрических функций, мне кажется, что должно быть наоборот. Ваше статья вроде бы подтверждает моё мнение, тем не менее, я не знаю, как обстоит дело на самом деле (т.е. как устроен расчет sin в Mathematica или Matlab)

avitek Автор
10.09.2021 14:31+1Решая уравнение 0 = cos(n*arccos(x)), находят корни полинома. У меня это сделано примерно так же (строки 149-162).

belch84
10.09.2021 14:55Корни можно найти однажды, хранить в таблице и использовать постоянно. У вас в программе написано
, но вычисление функции cosl должно же быть как-то организовано компилятором? Вообще, интересно, как устроено вычисление тригонометрической функции в математическом пакете или языке высокого уровня. Подозреваю, что это делается при помощи интерполяции полиномами (возможно, полиномами Чебышева).T val = cosl(M_PI * (0.5 + i) / n);
avitek Автор
10.09.2021 15:16Вообще, интересно, как устроено вычисление тригонометрической функции в математическом пакете или языке высокого уровня. Подозреваю, что это делается при помощи интерполяции полиномами (возможно, полиномами Чебышева).
Знатоком не являюсь, но по своему опыту могу сказать, что очень разными, зависит от платформы. На платформе x86 FPU вычисляет синус одной инструкцией fsin. На STM32 со встроенной плавающей точкой идёт много вызовов разных функций, сильно не вникал. На целочисленных CPU ещё сложнее.
На ПК, если ничего не путаю, считается первый квадрант полиномом с нечётными степенями.Корни можно найти однажды, хранить в таблице и использовать постоянно.
Эта программа для создания таблиц на ПК, и быстродействие не важно, если вы об этом. Вычисление корней полинома нужной степени "на лету" мне кажется более элегантным и универсальным.

belch84
10.09.2021 15:43Знатоком не являюсь, но по своему опыту могу сказать, что очень разными, зависит от платформы. На платформе x86 FPU вычисляет синус одной инструкцией fsin.
Я тоже не знаток, исхожу из здравого смысла. Даже если процессор с плавающей точкой реализует вычисление тригонометрической функции одной инструкцией, все равно где-то у него внутри должна быть микропрограмма (или что-то подобное, не знаю, как оно называется), которая сведет вычисления sin к операциям сложения и умножения чисел (и еще, возможно, поиска в предопределенной таблице). Поэтому, мне кажется, значения тригонометрических функций должны вычисляться не так уж и медленно, и порядок именно такой — sin вычисляется с помощью полинома, а не наоборот, и схема должна быть примерно такой, как вы описываете или похожей (повторюсь, это мое личное мнение)

MichaelBorisov
19.10.2021 19:13На x86 для аппаратного вычисления синусов, скорее всего, используется алгоритм CORDIC. Этот же алгоритм используется в библиотеках для FPGA.

encyclopedist
10.09.2021 15:38+3Во-первых, в x86 ЦПУ есть просто инструкции синуса и косинуса.
-
Если встроенные инструкции не использовать, (например, для векторизации, для воспроизводимости, или когда инструкции недоступны), то используется некий полином. Например, вот что делает библиотека SLEEF: https://github.com/shibatch/sleef/blob/85440a5e87dae36ca1b891de14bc83b441ae7c43/src/libm/sleefdp.c#L789-L840
(сначала аргумент приводится к определенному диапазону, и затем используется полином 8 порядка)
Update: вот реализация из musl libc (в свою очередь, основана на реализации из freebsd):
static const double S1 = -1.66666666666666324348e-01, /* 0xBFC55555, 0x55555549 */ S2 = 8.33333333332248946124e-03, /* 0x3F811111, 0x1110F8A6 */ S3 = -1.98412698298579493134e-04, /* 0xBF2A01A0, 0x19C161D5 */ S4 = 2.75573137070700676789e-06, /* 0x3EC71DE3, 0x57B1FE7D */ S5 = -2.50507602534068634195e-08, /* 0xBE5AE5E6, 0x8A2B9CEB */ S6 = 1.58969099521155010221e-10; /* 0x3DE5D93A, 0x5ACFD57C */ double __sin(double x, double y, int iy) { double_t z,r,v,w; z = x*x; w = z*z; r = S2 + z*(S3 + z*S4) + z*w*(S5 + z*S6); v = z*x; if (iy == 0) return x + v*(S1 + z*r); else return x - ((z*(0.5*y - v*r) - y) - v*S1); }

Refridgerator
10.09.2021 20:04Мне по-прежнему очень хочется посмотреть, как вы будете вычислять многочлен Чебышева миллионной степени хотя бы схемой Горнера. И сравнить результаты по затраченному времени и точности полученного значения.

belch84
10.09.2021 20:51+2Ну, мы же с вами уже все обсудили, для милионной степени придется считать через косинусы. Я могу даже построить график многочлена милионной степени, вообще не прибегая к вычислению его значений
Полином Чебышева милионного порядка
Ну, это потому, что здесь у него миллион корней
Но вот для небольших порядков, вроде единиц-десятков, считать их значения через косинусы мне кажется нецелесообразным. Наоборот (наоборот!), есть смысл вычислять косинусы с помощью полиномов Чебышева.
Не имея большого опыта работы с полиномами Чебышева, хотел тем не менее поинтересоваться — часто ли в реальной жизни нужно вычислять значения этих полиномов порядка миллион, да еще вне их естественной области определения? И какого порядка ошибки при этом возникают? В вашей последней публикации таки появились числа типа 0.9 + 10^-16i, которые показывают, что комплексные числа тоже могут вызывать проблемы (возможно, в этом конкретном случае без них не обойтись, но и с ними тоже приходится задумываться)
Refridgerator
10.09.2021 22:04+1есть смысл вычислять косинусы с помощью полиномов Чебышева.
В некоторых случаях — да, есть, и в моей последней статье такой случай тоже упоминается при вычислении окна Нуталла (причём результат получен аналитически, а не численно, и такой фокус тоже не всегда срабатывает). Так как вычисляет автор статьи — не факт, потому что есть методы поэффективнее (но спорить не буду).Не имея большого опыта работы с полиномами Чебышева, хотел тем не менее поинтересоваться — часто ли в реальной жизни нужно вычислять значения этих полиномов порядка миллион, да еще вне их естественной области определения?
Есть такая оконная функция — Дольфа-Чебышева, которая как раз считается через многочлены Чебышева, в том числе и за пределами диапазона (-1;1). А степень многочлена Чебышева в ней линейно зависит от количества отсчётов оконной функции, и окно длиной всего лишь в секунду может занимать 192000 отсчётов. До миллиона, как видите, совсем недалеко (а мой спектроанализатор поддерживает семплы до 8 миллионов отсчётов — что тоже не так уж и много при пересчёте на минуты).

mobi
10.09.2021 20:53Первое, что приходит в голову — записать рекуррентное соотношение для многочленов Чебышева в матричном виде и воспользоваться алгоритмом быстрого возведения в степень. Для миллионной степени будет примерно 20 итераций, что не так уж и много.

Refridgerator
10.09.2021 22:07Тоже было бы интересно на это посмотреть, потому что в матричных вычислениях я не силён.

mobi
11.09.2021 10:58Ну это примерно как быстрый расчет чисел Фибоначчи (кажется, даже на Хабре когда-то был разбор этого метода).
Кстати, как следствие матричной записи, можно привести матрицу к диагональному виду и получить ответ в известном виде (правда, с использованием комплексных чисел):
Tn(x) = { [x+i√(1−x2)]n + [x−i√(1−x2)]n } / 2.
Refridgerator
11.09.2021 11:23Формула через комплексные числа просто обобщает многочлены 1-го и и 2-го рода и выводится напрямую через косинус аркосинуса, без какого-либо участия матриц.

Refridgerator
11.09.2021 12:49+1Рекуррентно вычислить многочлен Чебышева можно и без всяких матриц, например:
ChebyshevT[27, x] = ChebyshevT[3, ChebyshevT[3, ChebyshevT[3, x]]]

AVDerov
11.09.2021 22:12Так вычислять полиномы Чебышева имеет смысл для высоких степеней, что бы избежать ошибок вычисления высоких степеней и суммирования близких величин.

YuriyVorobyov1333
10.09.2021 14:20+2Ссылки на гит сбились, выдает 404

0serg
10.09.2021 15:05+1Для расчета референсных значений можно использовать boost::multiprecision.
Разница в точности между ARM и x86 не может ли быть связана с разными ключами компиляции? Разные там strict / fast math? А свежие MSVC компиляторы, к примеру, вообще не умеют в 80-битный long double, у них всегда 64 бита. Какие компиляторы и настройки использовались?
avitek Автор
10.09.2021 15:23Какие компиляторы и настройки использовались?
Везде gcc, настроек минимум. Я не являюсь знатоком компиляторов - меняю настройки, только если совсем собираться не хочет.
В разных проектах встречаются скрипты (*.cmd, *.sh) для компиляции, можете взглянуть.А свежие MSVC компиляторы, к примеру, вообще не умеют в 80-битный long double, у них всегда 64 бита.
Хм. Не зря я их не люблю...
Для расчета референсных значений можно использовать boost::multiprecision
Спасибо!

encyclopedist
10.09.2021 15:47+4Помимо максимальной ошибки, для тригонометрических функций часто важны и другие свойства:
Непрерывность
Дифференцируемость
Правильные значения при "специальных" значениях аргумента (0, 30, 45, 60, 90, ...)
Непревышение 1 модуля значения (чтобы не получить сюрпризы при `sqrt(1 - sin^2)`)

avitek Автор
10.09.2021 20:54Могут быть проблемы с последним пунктом на некоторых комбинациях длины таблицы / степени полинома.
Остальные же будут выполняться в пределах заданной точности.

neurocore
11.09.2021 15:03+1А чем не устроило разложение в ряд Тейлора? Вычисляется просто, итеративно, остаточный член O(x^2n)

runaway
11.09.2021 15:27Присоединяюсь к вопросу. В любом калькуляторе все функции через эти ряды считаются.

avitek Автор
11.09.2021 20:04разложение в ряд Тейлора
А вот кстати...
Здесь автор этим и занимается, делая основной упор на точности вычислений с плавающей точкой (формула оттуда же):Было бы интересно сравнить оба метода по точности и быстродействию на фиксированной точке. Возможно, займусь в обозримом будущем

Refridgerator
11.09.2021 20:17У ряда Тейлора есть нюанс — чем дальше от точки разложения функции, тем больше расхождение. Поэтому при одной и той же степени многочлена ряд Тейлора даёт далеко не самое лучшее приближение среди всех возможных.

SGordon123
10.10.2021 09:06Это понятно что приближение хуже, нет нигде сравнений что для тех же, положим 40 бит в арме потребуется такая то степень , а чебышева такая то?

avitek Автор
11.09.2021 20:53чем не устроило разложение в ряд Тейлора
Подумал немного, и готов дать ответ.
Рядом Тейлора синус считают, емнип, только для первого квадранта, и там целевая функция непрерывна. В методе, описанном в статье, есть похожий случай, когда таблица состоит из 4 строк, и в этом случае аппроксимация полиномами Чебышёва может дать худший результат при том же количестве операций умножения (я исхожу из того, что степени Х в рядах Тейлора растут в 2 раза быстрее. Поправьте меня, если ошибаюсь).
Но при использовании рядов Тейлора я не вижу способа аппроксимации небольшого интервала, например от 110/256 до 111/256 части полного оборота. А полиномами Чебышёва это можно сделать, найдя корни именно для этого промежутка. Такое сужение диапазона аргумента даст прирост точности, что можно конвертировать в уменьшение кол-ва математических операций при снижении точности до нужного значения.
Но сравнение обоих методов на 1-м квадранте, целыми числами, я всё-таки сделаю. Наверное...

DrSmile
12.09.2021 06:55+1На практике при аппроксимации функций не пользуются ни Тейлором, ни Чебышевым. В лучшем случае они подходят в качестве начальных приближений. Просто прогоняют L∞-оптимизацию коэффициентов, а в тяжелых случаях (когда нужны последние ULPы) — прямой перебор последних битов в окрестности оптимума.

Sdima1357
21.09.2021 17:23+1<Рядом Тейлора синус считают, емнип, только для первого квадранта, и там целевая функция непрерывн...>
Вы неправильно помните.
Разложение точки в окрестности 0 это только частный случай ряда Тейлора - ряд Маклорена. Ряд Тейлора применим для окрестности любой точки, а не только 0.

Antiminddamping
12.09.2021 21:17А почему нет сравнения с другими методами аппаратного вычисления приближения синуса, например, CORDIC (кстати там выше ссылка была в одном из комментариев)?
У последнего, кстати, очень удобная интерпретация вычисления в битах, т.к., собственно, каждый шаг уточнения является сложением и делением на два (сдвиг на бит).
Даже если тот же CORDIC не может дать нужную точность или, например, на МК считается плохо (на ПЛИС, кстати, очень даже хорошо работает, т.к. там очень хорошее целочисленное представление получается), то всё равно можно было бы уделить этому хотя бы пару абзацев.
Кстати, по поводу МК (пусть и на ARM-ядре) - уже сейчас есть STM32G4 с CORDIC-сопроцессором на борту (https://www.compel.ru/lib/140072).
avitek Автор
13.09.2021 07:38А почему нет сравнения с ...
Я не преследовал такую цель.
Но Вам, я думаю, ничто не мешает сделать это самостоятельно и поделиться здесь результатами. А мы бы с удовольствием это почитали.

byman
13.09.2021 09:42А куда же делись 10 бит, я так и не понял. Есть подозрение, что точность, равная разрядности мантиссы на 32- и 64-битных float получалась за счёт запаса 80-битных вычислений, результаты которых потом огрублялись до заданных 32 и 64, а без огрубления она как раз составляла те самые 54 бита. При вычислениях на ARMах с 64-битным FPU точность вычисления упала до 50.8 бита против 53 на x86/x64.
правильно ли я понимаю, что у вас все исходные данные были с 80-бит точностью и результат был доступен в формате 80-бит, но точность получилась все равно duble? Была на хабре очень интересная статья про синус-косинус и там приводился пример пакета для вычислений с double-double и quad-double точностью. Считает медленно, но если нужен более точный результат, то очень хорошая штука.

avitek Автор
13.09.2021 17:56правильно ли я понимаю, что у вас все исходные данные были с 80-бит точностью и результат был доступен в формате 80-бит
Нет. Исходные данные, как и промежуточные результаты заданы либо 32, либо 64, либо 80 бит float, зависит от значения TABLE_TYPE.
Но внутри FPU все вычисления производятся в формате 80 бит. И я не уверен, что компилятор (точнее код, им сгенерённый) гоняет промежуточные результаты между FPU и памятью, огрубляя их. То есть, независимо от типа TABLE_TYPE, все вычисления скорее всего производятся как 80-битные, и только в самом конце происходит огрубление (приведение к типу).

Refridgerator
28.09.2021 08:45Проблемы с точностью вычислений у вас возможно возникли из-за нехватки точности double при вычислении коэффициентов многочленов Чебышева. Поэтому более разумно для вычисления коэффициентов аппроксимирующего многочлена использовать мат. пакет (или соответствующую библиотеку) с точностью, скажем, 100 знаков после запятой, а результаты округлить.

Refridgerator
28.09.2021 10:23Вот мой проверочный код на си-шарпе, считающий разницу от библиотечной функции на ста миллионах точках, равномерно распределённых в диапазоне от 0 до 1:
кодclass Program { static double ChebyshevSin(double x) { double xx = x * x; return x*(1.570796326794895 + xx*(-0.6459640975061731 + xx*(0.07969262624514188 + xx*(-0.004681754128869211 + xx*(0.0001604411632629485 + xx*(-3.598802460206541e-6 + xx*(5.687768400923302e-8 - 6.434815323635176e-10*xx))))))); } static void Main(string[] args) { double max = 0.0; int count = 100000000; for (int i = 0; i < count; i++) { double x = i / (double)count; double y = Math.Sin(x * Math.PI / 2.0) - ChebyshevSin(x); max = Math.Max(max, Math.Abs(y)); } Console.WriteLine("max error: {0}",max); Console.ReadKey(); } }
Максимальное отклонение составило 5.55*10-16, то есть как минимум 15 знаков после запятой совпадают. Также на SSE код можно ускорить почти в два раза, если разбить многочлен на два и считать параллельно, а результаты сложить.
0serg
28.09.2021 11:39Это 51 бит точности (в определении автора) а у него получалось 54 бита (ошибка менее 1e-16)

Refridgerator
28.09.2021 11:48Так тут и решение «в лоб», без разбивки на диапазоны. Понятно, что при меньших степенях и погрешность будет меньше. На FPU, думаю, и к 20 десятичным знакам можно приблизиться, по крайней мере Wolfram её показывает (на полиноме большей степени).

Refridgerator
28.09.2021 12:10Да и сравнивать надо не с библиотечной реализацией, а во внешнем мат. пакете с гарантированно перекрывающей точностью.

Refridgerator
28.09.2021 13:28+1Ладно, вот этот вариант (перенормированный обратно к (-pi/2, pi/2))
коддал 53 бита совпадения с библиотечным синусом шарпа. Вполне неплохой результат для столь простой реализации, по-моему.static double ChebyshevSin(double x) { double xx = x * x; return x * (0.9999999999999999980 + xx * (-0.1666666666666666190 + xx * (0.00833333333333299283 + xx * (-0.0001984126984115937723 + xx * (2.75573192045707547e-6 + xx * (-2.50521063803320390e-8 + xx * (1.605891861118114436e-10 + xx * (-7.64251091766084203e-13 + 2.71665816482462532e-15 * xx)))))))); }

Refridgerator
28.09.2021 14:17UPD: подцепил к шарпу Wolfram через .Net Link, итого на 100000 замерах:
библиотечная: 50.6 бит,
Чебышевым: 50.45 бит.
Разницу считал тоже в Wolfram-е.
Refridgerator
29.09.2021 13:19UPD: забыл в предыдущем случае масштабировать диапазон испытуемых значений с 1 до pi/2. На полном диапазоне в обоих случаях точность снизилась ещё на 2 бита. Похоже, вопрос с точностью библиотечных реализаций требует отдельного более пристального рассмотрения. Я также не уверен в корректности передаваемых в Wolfram значений, поскольку использовал метод .ToString() для преобразования double к строковому десятичному типу. В любом случае я уверен, что если точность в одном-двух последних знаках имеет критически важное значение — то нужно переходить на extended, quadruple или double-double, а не вымучивать пару бит дополнительной точности.



dom1n1k
Функция smoothstep аппроксимирует синус с хорошей точностью.
Refridgerator
Какая же это хорошая точность, если разницу невооружённым глазом видно?
dom1n1k
Для своей предельной простоты и скорости - точность неплохая. Понятно, что это не для научных/технических расчетов, это для задач типа игровой анимации - точность на глаз достаточная, скорость больше некуда.
Refridgerator