Должен сразу сказать, что в boost есть библиотека graph, но при беглом ее просмотре было совершенно не очевидно, какие преимущества она дает в решении относительно простых задач. Кроме того, возникли опасения, что на то, чтобы разобраться с ней уйдет слишком много времени, о boost::graph написана целая книга. Ну, а если обозримые задачи можно решить в лоб и быстро, то почему бы не попробовать, а boost::graph оставить до лучших времен.

Итак, граф сущность довольно простая, он состоит из вершин и ребер, в которых есть какая-то полезная информация. Ребра можно реализовать так:

template <class V, class E>
class Edge
{
public:
	Edge(const E& properties, Vertice<V, E>* vertice1, Vertice<V, E>* vertice2)
		: properties_(properties)
		, vertice1_(vertice1)
		, vertice2_(vertice2)
	{}
	const Vertice<V, E>* getVertice1() const { return vertice1_; }
	const Vertice<V, E>* getVertice2() const { return vertice2_; }
	const E* getProperties() const { return &properties_; }
private:
	const E properties_;
	Vertice<V, E>* vertice1_;
	Vertice<V, E>* vertice2_;
};

Думаю, что тут и так все понятно, но есть одна деталь: если ребро ориентированное - один из указателей будет нулевым. Или можно еще так сказать: указатель на вершину указывает направление ребра. Такая реализация приводит к тому, что впустую расходуется указатель у ориентированных ребер, но сэкономить, к сожалению, не получится. Можно реализовать ориентированное ребро с одним указателем, сделать его потомком неориентированное ребро, добавив туда еще один указатель, и использовать виртуальные функции, но тогда добавится указатель на таблицу виртуальных функций и расход памяти даже увеличится.

Реализация вершины тоже довольно проста:

template <class V, class E>
class Vertice
{
public:
  Vertice(const V& properties) : properties_(properties) {}
	const V* getProperties() const { return &properties_; }
	const std::vector<Edge<V, E>*>* getEdges() const { return &edges_; }
	void addOrderedEdge(const E& properties, Vertice<V, E>* target)
	{
		Edge<V, E>* edge = new Edge<V, E>(properties, target, nullptr);
		edges_.push_back(edge);
	}
	void addEdge(const E& properties, Vertice<V, E>* target)
	{
		Edge<V, E>* edge = new Edge<V, E>(properties, target, this);
		edges_.push_back(edge);
		target->edges_.push_back(edge);
	}
private:
	const V properties_;
	std::vector<Edge<V, E>*> edges_;
};

edges_ содержит указатели на исходящие ребра вершины и это дает возможность подумать о еще одном варианте экономии. Также как и в первом варианте можно использовать наследование, но без виртуальных функций, ориентированные и неориентированные ребра разделять в векторе нулевым указателем и использовать приведение типов. Даст ли это экономию? Далеко не факт, мы избавляемся от указателя в одном месте, но он добавляется в другом. А вот, что точно факт, так это то, что код усложнится. Поэтому, вспоминаем, что графы у нас используются небольшие, успокаиваем себя словами Дональда Кнута, что преждевременная оптимизация корень всех бед, и оставляем все как есть.

Чтобы сделать дальнейший рассказ более наглядным, предположим, что у нас есть такой граф и все дальнейшие рассуждения будем вести на его основе.

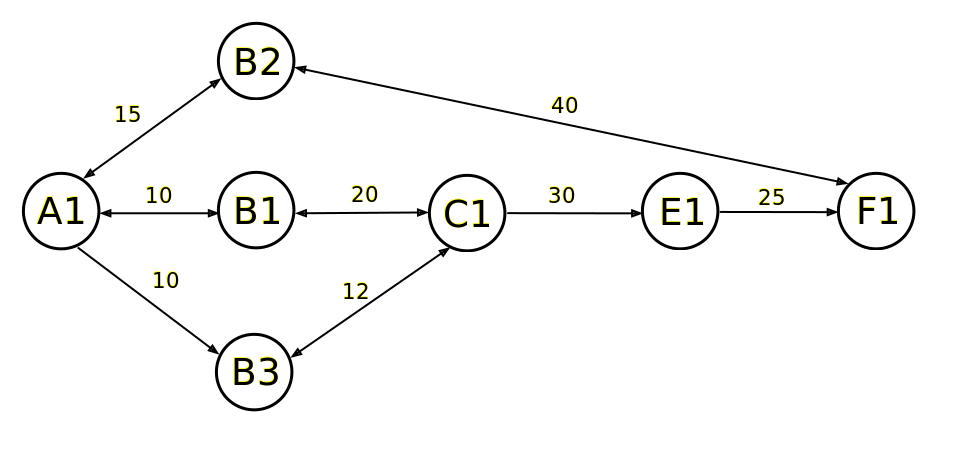
Для начала создадим граф:

Vertice<std::string, int> a1("A1");
Vertice<std::string, int> b1("B1");
a1.addEdge(10, &b1);
Vertice<std::string, int> c1("C1");
b1.addEdge(20, &c1);
Vertice<std::string, int> b2("B2");
a1.addEdge(15, &b2);
Vertice<std::string, int> e1("E1");
c1.addOrderedEdge(30, &e1);
Vertice<std::string, int> f1("F1");
e1.addOrderedEdge(25, &f1);
b2.addEdge(40, &f1);
Vertice<std::string, int> b3("B3");
a1.addOrderedEdge(10, &b3);
b3.addEdge(12, &c1);

И будем искать какой-нибудь путь из вершины А1 в вершину В3 и его стоимость. Для этого можно использовать обход граф в глубину, в процессе обхода будем запоминать пройденные вершины и суммировать стоимость дуг. На графе обход будет выглядеть так, шаги обхода пронумерованы:

Глядя на этот обход можно отметить пару моментов:

• путь не обязательно приведет к успеху и придется возвращаться назад (шаги 3-10)

• в процессе обхода можно попасть в уже пройденные вершины и тогда нужно прекращать обход и откатываться назад (шаг 6)

С учетом сказанного реализация может выглядеть так:

bool search(const Vertice<std::string, int>* vertice, const std::string& name, std::vector<const Vertice<std::string, int>*>* visited, int* cost)
{
	if (std::find(visited->begin(), visited->end(), vertice) != visited->end())
	{
		return false;
	}
	visited->push_back(vertice);
	if (*vertice->getProperties() == name)
	{
		return true;
	}
	for (const Edge<std::string, int>* edge : *vertice->getEdges())
	{
		const Vertice<std::string, int>* next = edge->getVertice1() == vertice || edge->getVertice1() == nullptr ? edge->getVertice2() : edge->getVertice1();
		if (search(next, name, visited, cost))
		{
			*cost += *edge->getProperties();
			return true;
		}
	}
	visited->pop_back();
	return false;
}

Это рекурсивная функция делает следующее:

1. Проверяет, что вершина еще не была пройдена и формирует список пройденных вершин

2. Завершает рекурсию, если вершина была найдена

3. Рекурсивно вызывает себя для соседних вершин

4. Если вершина была найдена - суммирует пройденные дуги

Что можно сказать об этой функции?
Она работает и это, пожалуй, единственное ее достоинство.
А вот что можно сказать о недостатках:

1. Слишком многословная, основная часть кода - обход графа, а самое интересное - работа с данными вершин и дуг, занимает всего пару строчек и теряется на фоне остального кода. Причем во времена до 11 стандарта, когда не было ни range-based for, ни auto, она была еще более громоздкой.

2. Этот код не получится использовать повторно. Например, проверка на посещение уже пройденных вершин будет полезен для подавляющего большинства алгоритмов, но повторно его использовать при такой реализации мы не сможем.

3. Такой код провоцирует копипаст со всеми вытекающими из него опечатками и ошибками. После второго похода в отладчик было решено срочно с этим что-то делать.

Тут естественно возникает желание разделить обход графа и работу с вершинами и дугами. И для этого хорошо подойдет что-то типа паттерна посетитель. С учетом того, динамический полиморфизм нам не нужен - будем использовать шаблоны. Для начала нужно понять какие должны быть методы у посетителя и их сигнатура. Очевидно, что должны быть два метода: visitVertice и visitEdge, котрые будут обрабатывать соответствующее объекты. А если посмотреть на функцию search, то становится очевидно, что visitVertice должна возвращать true или false, которое указывает, следует ли остановить обход или продолжать, аналогично и для visitEdge. Но этого недостаточно, нужен код, который выполнит суммирование стоимости дуг и удаление вершин при выходе из рекурсивного вызова, поэтому добавим еще функции leaveVertice и leaveEdge. Исходя из всего этого алгоритм обхода в глубину можно реализовать так:

template <class V, class E, class F>
void depthPass(const Vertice<V, E>* vertice, F* visitor)
{
	if (!visitor->visitVertice(vertice))
	{
		return;
	}
	for(Edge<V,E>* edge : *vertice->getEdges())
	{
		if (!visitor->visitEdge(edge))
		{
			continue;
		}
		const Vertice<V, E>* next = edge->getVertice1() == vertice || edge->getVertice1() == nullptr ? edge->getVertice2() : edge->getVertice1();
		depthPass(next, visitor);
		visitor->leaveEdge(edge);
	}
	visitor->leaveVertice(vertice);
}

И теперь можно реализовать простой, но очень полезный посетитель. Он не будет делать ничего особенного, просто защищать алгоритм от зацикливания:

template <class V, class E>
class OneTimeVisitor
{
public:
	bool visitVertice(const Vertice<V, E>* vertice)
	{
		if (std::find(visited_.begin(), visited_.end(), vertice) != visited_.end())
		{
			return false;
		}
		visited_.push_back(vertice);
		return true;
	}
	bool visitEdge(const Edge<V,E>*)
	{
		return true;
	}
	void leaveVertice(const Vertice<V, E>*) { visited_.pop_back(); }
	void leaveEdge(const Edge<V, E>* ) {}
	const std::vector<const Vertice<V,E>*>& getVisited() const { return visited_; }
private:
	std::vector<const Vertice<V,E>*> visited_;
};

Как несложно заметить, этот полностью дублирует код из search, но теперь другие посетители могут наследоваться от OneTimeVisitor и повторно использовать его код. Или можно так сказать: OneTimeVisitor обеспечивает посещение всех вершин графа один раз. Теперь можно вернуться к функции search и реализовать ее в виде посетителя. При этом расширим ее возможности, чтобы она искала не один путь, а заданное количество путей. И для начала реализуем просто поиск пути без подсчета стоимости. Почему так? Чтобы повторно использовать код. Поиск пути - достаточно абстрактный алгоритм, который может быть реализован, используя только оператор сравнения. А подсчет стоимости значительно больше привязан к данным ребер. Объединяя эти операции в одном посетителе мы сильно снижаем возможность его повторного использования.

template <class V, class E, class C = std::equal_to<V>>
class PathBuilder : public OneTimeVisitor<V, E>
{
public:
	PathBuilder(const V& value, size_t pathCount = std::numeric_limits<size_t>::max())
		: value_(value)
		, pathCount_(pathCount)
		, pathes_(new std::vector<std::vector<const Vertice<V, E>*>>())
	{}
	bool visitVertice(const Vertice<V, E>* vertice)
	{
		if (!OneTimeVisitor<V, E>::visitVertice(vertice))
		{
			return false;
		}
		if (C()(*vertice->getProperties(), value_))
		{
			pathes_->push_back(OneTimeVisitor<V, E>::getVisited());
			OneTimeVisitor<V, E>::leaveVertice(vertice);
			return false;
		}
		return true;
	}
	bool visitEdge(const Edge<V,E>* edge)
	{
		if (!OneTimeVisitor<V, E>::visitEdge(edge))
		{
			return false;
		}
		if (pathes_->size() < pathCount_)
		{
			return true;
		}
		OneTimeVisitor<V, E>::leaveEdge(edge);
		return false;
	}

private:
	const V value_;
	const size_t pathCount_;
	std::shared_ptr<std::vector<std::vector<const Vertice<V, E>*>>> pathes_;
};

Здесь нужно обратить внимание на следующий момент: если метод visit* базового класса вернул true, а метод производного класса собирается вернуть false, то должен быть вызван соответствующий метод leave базового класса. В противном случае посетитель будет в рассинхронизированном состоянии: члены базового класса будут в состоянии, как если бы посетитель посетил текущий узел или ребро, а члены производного класса нет. Причина использования shared_ptr будет объяснена позже - это задел для дальнейшего развития библиотеки.

Посетитель для поиска путей и стоимостей может реализовать наследуясь от PathBuilder. Но можно было бы наследоваться от OneTimeVisitor и повторить логику PathBuilder, возможно, так было бы проще. Это скорее дело вкуса и предпочтений.

template <class V, class E, class C = std::equal_to<V>>
class PathCostBuilder : public PathBuilder<V, E, C>
{
public:
	PathCostBuilder(const V& value, size_t pathCount = std::numeric_limits<size_t>::max())
		: PathBuilder<V, E, C>(value, std::numeric_limits<size_t>::max())
		, pathCount_(pathCount)
		, cost_(0)
		, costs_(new std::multimap<int, int>())
	{}
	bool visitVertice(const Vertice<V, E>* vertice)
	{
		size_t oldPathesSize = PathBuilder<V, E, C>::getPathes().size();
		if (!PathBuilder<V, E, C>::visitVertice(vertice))
		{
			if (PathBuilder<V, E, C>::getPathes().size() != oldPathesSize)
			{
				if (costs_->size() == pathCount_ && cost_ < (--costs_->end())->first)
				{
					auto lastItem = --costs_->end();
					getPathes().erase(getPathes().begin() + lastItem->second);
					costs_->erase(lastItem);
				}
				if (costs_->size() < pathCount_)
				{
					costs_->emplace(cost_, PathBuilder<V, E, C>::getPathes().size() -1);
				}
			}
			return false;
		}
		if (costs_->size() == pathCount_ && cost_ >= (--costs_->end())->first)
		{
			PathBuilder<V, E, C>::leaveVertice(vertice);
			return false;
		}
		return true;
	}
	bool visitEdge(Edge<V,E>* edge)
	{
		if (!PathBuilder<V, E, C>::visitEdge(edge))
		{
			return false;
		}
		cost_ += *edge->getProperties();
		return true;
	};
	void leaveEdge(Edge<V, E>* edge)
	{
		cost_ -= *edge->getProperties();
	}
private:
	size_t pathCount_;
	int cost_;
	std::shared_ptr<std::multimap<int, int>> costs_; // cost, path position pairs
};

За кадром остался вопрос деструктора Vertice. Здесь ничего сложного, но нужно помнить, что ребра создаются в классе вершин, а значит они должны и удаляться там же. Кроме того, если ребро неориентированное, то ребро должно быть удалено из списка ребер еще одного узла:

~Vertice()
{
	for(Edge<V, E>* edge : edges_)
	{
		if (edge->vertice1_ != nullptr && edge->vertice2_ != nullptr)
		{
			Vertice<V, E>* other = (edge->vertice1_ == this ) ? edge->vertice2_ : edge->vertice1_;
			other->edges_.erase(std::find(other->edges_.begin(), other->edges_.end(), edge));
		}
		delete edge;
	}
}

Поскольку очень часто узлы будут создаваться динамически, например, описание графа может быть в файле, а сохраняться только указатель на один узел из которого будет выполняться все расчеты, то реализуем посетитель, который будет собирать все вершины графа для последующего удаления. Но чтобы сделать посетитель более универсальным добавим еще один параметр, который определяет максимальное удаление собираемых вершин от стартового. По умолчанию ограничения нет, а 1 означает ближайших соседей:

template <class V, class E>
class VerticeCollector
{
public:
	VerticeCollector(size_t deptLimit = std::numeric_limits<size_t>::max())
		: deptLimit_(deptLimit)
		, dept_(0)
	{}
	bool visitVertice(const Vertice<V, E>* vertice)
	{
		return vertices_.insert(vertice).second;
	}
	void leaveVertice(const Vertice<V, E>* vertice)
	{
	}
	bool visitEdge(const Edge<V,E>*)
	{
		if (dept_ >= deptLimit_)
		{
			return false;
		}
		++dept_;
		return true;
	}
	void leaveEdge(const Edge<V, E>* )
	{
		--dept_;
	}
private:
	size_t deptLimit_;
	size_t dept_;
	std::unordered_set<const Vertice<V, E>*> vertices_;
};

Как видите, этот посетитель не наследуется от OneTimeVisitor поскольку это не дает никаких преимуществ.

Добавляя новые посетители можно реализовывать различные алгоритмы на графах. Для решения практических задач этого достаточно. Но есть еще один вариант обхода графа - обход в ширину. Теоретически он может дать лучший по скорости результат, если алгоритм не требует обхода всего графа, как, например, при поиске всех возможных маршрутов. Однако на практике это не обязательно так. Почему, станет понятно позже. Если внимательно прочитать описание обхода в глубину и в ширину, наример, на Википедии, и немного поразмыслить, то станет очевидно, что в первом случае алгоритм посещает соседей самой последней посещенной вершиной, а во втором первой еще не обработаной вершины. Такое поведение можно смоделировать с помощью стека (ведь не просто так использовалась рекурсивная функция, а стек вызавов функций называется стеком) и очереди. Таким образом, на первый взгляд может показаться, просто помещая указатели на вершины в разные контейнеры, получим разные типы обхода. Однако, за исключением простейших случаев, например, поиска узла, это не так. Проблема в том, что в процессе обхода пути на графе, посетитель может собирать необходимую ему информацию, например, подсчитывать стоимости, а при обходе в ширину осуществляется обход одновременно нескольких путей. Однако в простешем случае, если посетитель не изменяет своего состояния при посещении вершин, как, например, при поиске вершины, это сработает.

template <class V, class E, class F>
void dummyBreadthPass(const Vertice<V, E>* vertice, F* visitor)
{
	std::queue<const Vertice<V, E>*> vertices;
	vertices.push(vertice);
	while (!vertices.empty())
	{
		const Vertice<V, E>* current = vertices.front();
		vertices.pop();
		if (!visitor->visitVertice(current))
		{
			continue;
		}
		for(Edge<V,E>* edge : *current->getEdges())
		{
			if (!visitor->visitEdge(edge))
			{
				continue;
			}
			const Vertice<V, E>* next = edge->getVertice1() == current || edge->getVertice1() == nullptr ? edge->getVertice2() : edge->getVertice1();
			vertices.push(next);
		}
	}
}

Эта функция очень похожа на depthPass. Ее принципиальное отличие в отсутствии методов leaveVertice и leaveEdge, поскольку мы не можем накапливать информацию при обходе графа, то и восстанавливать ее в исходное состояние нет никакого смысла.

И все же, как реализовать обход графа в ширину с произвольным посетителем? Очень просто, нужно для каждого пути использовать свой посетитель, а общую информцию, например, контейнер с результатами, сделать доступной всем экземплярам посетителя, например, через статический член класса или указатель:

template <class V, class E, class F, class Q>
void breadthPassCommon(const Vertice<V, E>* vertice, F* visitor)
{
	Q verticeQueue;
	verticeQueue.push(make_pair(vertice, new F(*visitor)));
	while (!verticeQueue.empty())
	{
		const Vertice<V, E>* vertice = verticeQueue.front().first;
		F* visitor = verticeQueue.front().second;
		verticeQueue.pop();
		if (!visitor->visitVertice(vertice))
		{
			continue;
		}
		bool visitorPassed = false;
		F tmpVisitor(*visitor);
		for(auto it = vertice->getEdges()->begin(); it != vertice->getEdges()->end(); ++it)
		{
			F* branchVisitor = visitor;
			if (visitorPassed)
			{
				branchVisitor = new F(tmpVisitor);
			}
			else
			{
				visitorPassed = true;
			}
			if (!branchVisitor->visitEdge(*it))
			{
				delete branchVisitor;
				continue;
			}
			const Vertice<V, E>* next = (*it)->getVertice1() == vertice || (*it)->getVertice1() == nullptr ? (*it)->getVertice2() : (*it)->getVertice1();
			verticeQueue.push(make_pair(next, branchVisitor));
		}
		if (!visitorPassed)
		{
			delete visitor;
		}
	}
}

Хочу обратить внимание, что в очереди хранится не только указатель на узел, но и посетитель, который копируется при обходе каждого нового пути, это очень расточительно с точки зрения памяти, если узлы имеют много дуг, а посетители хранят много информации. Очередь сделана параметром шаблона, чтобы можно было использовать обычную очередь и очередь с приоритетом. Очередь с приоритетом лучше подойдет, если по каким-либо данным можно выбрать наиболее перспективный путь. Например, при поиске кратчайшего пути можно первыми обрабатывать пути с минимальной стоимостью.

template <class V, class E, class F>
void breadthPass(const Vertice<V, E>* vertice, F* visitor)
{
	breadthPassCommon<V, E, F, std::queue<std::pair<const Vertice<V, E>*, F*>>>(vertice, visitor);
}

template <class V, class E, class F>
void priorityBreadthPass(const Vertice<V, E>* vertice, F* visitor)
{
	typedef std::pair<const Vertice<V,E>*, F*> QueueType;
	struct PairLess
	{
		bool operator()(const QueueType& a, const QueueType& b)
		{
			return *a.second < *b.second;
		}
	};
	class FrontAdapter : public std::priority_queue<QueueType, std::vector<QueueType>, PairLess>
	{
	public:
		const QueueType& front() const { return std::priority_queue<QueueType, std::vector<QueueType>, PairLess>::top(); }
	};
	breadthPassCommon<V, E, F, FrontAdapter>(vertice, visitor);
}