Прогнозирование – это важный инструмент экономики. Оно позволяет осуществлять рациональные закупки, вырабатывать долгосрочные планы действий или же, как в случае аудита, спрогнозировать будущие затраты. Прогнозирование так же является одной из областей Data Science.

Давайте рассмотрим создание простой прогнозной модели на основе линейного тренда с помощью эконометрических методов.

Возьмем некоторый набор данных (можно найти в репозитории Github, ссылка в конце статьи). Примем, что генезис не имеет значения (прим. автора – происхождение), но учтем, что данные имеют нормальное распределение:

import pandas as pd
excel_data_df = pd.read_excel('analysis.xlsx')
excel_data_df.head()

Первым этапом нашей работы является сглаживание. Самый простой метод сглаживания рядов – это скользящее среднее. Его смысл заключается в выделении нечетных последовательностей (3, 5, 7) и преобразование центральной точки в среднее арифметическое соседних значений. К примеру:

Есть так же формула взвешенной скользящей средней. Его отличие в том, что вес центральной точки при перерасчете удваивается:

Данный способ прост и легко применим. Однако имеет и свои недостатки: так, мы либо теряем крайние значения ряда, либо оставляем их в исходном виде.

Но, применим его с сохранением исходных крайних точек, остановившись на последовательности из трех элементов:

yts = []
yts.append(excel_data_df['yt'][0])
i=0
for element in excel_data_df['yt']:
  i=i+1
  if(i>excel_data_df['yt'].size-2):
    pass
  else:
    yts_per = (excel_data_df['yt'][i-1]+2*excel_data_df['yt'][i]+excel_data_df['yt'][i+1])/4
    yts.append(yts_per)
yts.append(excel_data_df['yt'][i-1])

На выходе получим новый столбец:

excel_data_df['yts'] = yts
excel_data_df.head()

Теперь построим графики, сравнив исходные данные и данные, после применения сглаживания (синий – исходные данные, оранжевый – сглаженные):

import matplotlib.pyplot as plt
plt.plot(excel_data_df['t'], excel_data_df['yt'])
plt.plot(excel_data_df['t'], excel_data_df['yts'])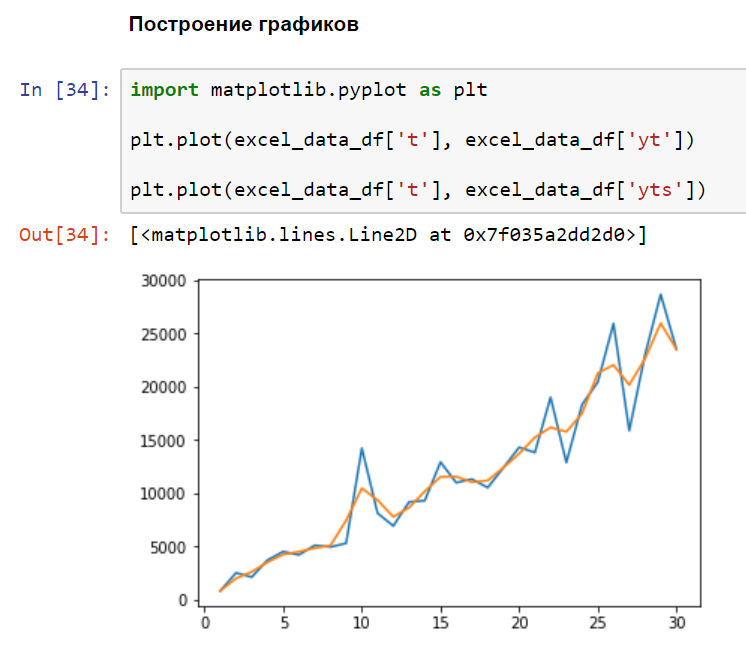

Наглядно видно, что всплески графика стали более схожими с реальной ситуацией. Теперь можно приступить к нахождению коэффициентов системы линейных алгебраических уравнений (СЛАУ), решение которой позволит нам получить веса формулы тренда нашего временного ряда.

t_list=excel_data_df['t'].values.tolist()
yts_list=excel_data_df['yts'].values.tolist()
i=0
t_sum=0
t2_sum=0
yts_sum=0
ytst_sum=0
while i<len(t_list):
  t_sum=t_list[i]+t_sum
  t2_sum=t_list[i]*t_list[i]+t2_sum
  yts_sum=yts_list[i]+yts_sum 
  ytst_sum=yts_list[i]*t_list[i]+ytst_sum
  i=i+1
print("Сумма по t:", t_sum, "| Сумма по t^2:", t2_sum, "| Сумма по yt:", yts_sum, "| Сумма по yt*t:", ytst_sum)

Первый коэффициент (возьмем за k1) – это количество значений ряда (t). В нашем случае – это 30.

Второй коэффициент (k2) – это сумма по t.

Третий коэффициент (k3) – сумма по t в квадрате.

Четвертый коэффициент (k4) – сумма значений ряда (y при t)

Пятый коэффициент (k5) – сумма по y умноженному на t. Получив эти данные, строим СЛАУ вида:

Подставим наши значения:

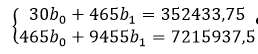
Теперь надо найти b0 и b1, воспользуемся библиотекой numpy:

import numpy as np
Matrix = np.array([[len(t_list), t_sum], [t_sum, t2_sum]]) 
Vektor = np.array([yts_sum, ytst_sum]) 
result_slau=np.linalg.solve(Matrix, Vektor)
print(result_slau)

Массив Matrix – это левая часть СЛАУ, массив Vektor – свободные члены или же правая часть СЛАУ.

Получив корни, можем построить функцию вида:

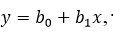
что и является линейным трендом.

Наш тренд:

для простоты восприятия.

b₁– это неслучайная функция, описывающая связь значения и времени, а b₀ — это случайное отклонение. Сверим полученную формулу с расчетами Excel:

Сверим полученную формулу с расчетами Excel:

На графике мы можем увидеть саму линию тренда, убедиться в правильности вывода нами формулы, а также увидеть значение R2. R2 – это коэффициент детерминации Пирсона, который рассчитывает на сколько данный тренд может точно описать временной ряд.

Грубо говоря – это точность прогноза. Значение больше 0,8 говорит о хорошей предсказуемости. Наша же модель имеет предсказуемость 0,96. При значении меньше 0,8, стоило бы обратить внимание на другие модели, допустим экспоненциальную и полиномиальную.

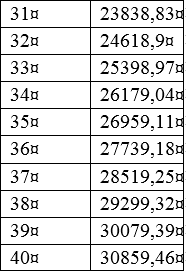
Таким образом, у нас получилось быстро и точно создать простейшую прогнозную модель. И, наконец, остается только посмотреть на полученный прогноз:

Код и исходные данные можно найти на: https://github.com/ikarteeva/econometrictrend