Как принять решение о покупке на основе 5-звездочных оценок от покупателей

Вам наверняка доводилось когда-либо в своей жизни принимать решение о покупке, основываясь на отзывах о товарах. Как социальным существам нам свойственно покупать вещи, которые рекомендуют другие покупатели.

Недавно, в поисках новых наушников, я просмотрел все товары, которые имеют оценку 5 звезд. Меня поразило, насколько сложно принять решение о покупке, основываясь только на отзывах покупателей. Мне пришло в голову взглянуть на отзывы товаров с точки зрения статистики.

В этой статье я объясняю метод оценки максимального правдоподобия на примере сравнения двух товаров, используя гипотетические оценки, полученные на основе мнений людей о товарах.

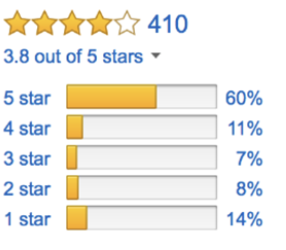
Если быть конкретным, то я смотрю на то, сколько раз товар получил оценку, отражающую степень удовлетворения людей этим товаром (от 1 до 5 звезд).

Оценка максимального правдоподобия — это метод, который определяет значения параметров модели. Значения параметров подбираются таким образом, чтобы они максимизировали вероятность того, что процесс написания отзыва о товаре, описанный моделью, дал оценку, которая будет более близка к реальной.

Давайте построим модель и оценим параметры таким образом, чтобы они максимизировали вероятность получения значений, наблюдаемых в реальных отзывах. Чтобы освежить в памяти вероятностные обозначения, упомянутые в этой статье, почитайте мою предыдущую статью по теме.

Мы хотим оценить θi — вероятность того, что люди оценят товар числом звезд равным i. Поскольку каждый новый рейтинг (оценка) имеет значение от 1 до 5, эта вероятность соответствует категориальному распределению Cat(θ).

Для каждого конкретного товара мы наблюдаем вектор рейтингов R= [r1,r2,r3,r4,r5]. Каждая оценка r_i — это общее количество i-звездных отзывов, полученных этим товаром.

Получение каждого i-звездного отзыва происходит с вероятностью θi. Поскольку каждый отзыв r независим от других, мы можем моделировать вероятность с помощью категориального распределения:

Вероятность наблюдения вектора событий R из N независимых отзывов задается полиномиальным распределением параметризованным θ:

Вычислить его логарифмическое правдоподобие можно следующим образом:

Что позволяет нам определить оценку максимального правдоподобия (Maximum Likelihood Estimator) θ для каждого из двух товаров. Для этого мы ищем θ, которая максимизирует правдоподобие L.

Обычно это делается путем дифференцирования функции правдоподобия по θ с использованием так называемых множителей Лагранжа.

Полагая, что все производные равны 0, мы получаем наиболее естественную оценку:

Следовательно, оценки максимального правдоподобия приведены ниже:

# количества звезд по отзывам
R_A = [10,6,10,27,109]
R_B = [57,33,29,45,246]

# оценки максимального правдоподобия
theta_A = R_A / np.sum(R_A)
theta_B = R_B / np.sum(R_B)

print("MLE for Product A: ", np.round(theta_A,3))
print("MLE for Product B: ", np.round(theta_B,3))

На основе этой оценки максимального правдоподобия θ для обеих моделей мы можем вычислить максимальное правдоподобие (Maximum Likelihood).

import math
import numpy as np

def f(n):
  return math.factorial(n)
  
def mle(R, theta):
  return (f(np.sum(R)) / (np.prod([f(r) for r in R]))) * \
         np.prod([theta[i]**R[i] for i in range(len(R))])

# максимальное правдоподобие
ml_A = mle(R_A,theta_A)
ml_B = mle(R_B,theta_B)

print("ML for Product A {:.7f}".format(ml_A))
print("ML for Product B {:.7f}".format(ml_B))
ml_products.py

Дает ли максимальное правдоподобие уверенность в том, что один из товаров предпочтительнее в глазах покупателей? Ответ не однозначен.

Здесь в игру вступает информационный критерий Акаике (Akaike Information Criterion), который дает нам некоторую доказательную базу. Оценка по информационному критерию Акаике награждает модели, которые достигают высокого показателя критерия адекватности (с низким максимальным правдоподобием), и штрафует модели, если они становятся чрезмерно сложными (большое количество параметров k).

Предпочтительной является модель с минимальным значением информационного критерия Акаике и максимальным правдоподобием, как показано ниже.

# информационный критерий Акаике
aic_A = 2*5 - 2*math.log(ml_A)
aic_B = 2*5 - 2*math.log(ml_B)
print("AIC for Product A: {:.2f}".format(aic_A))
print("AIC for Product B: {:.2f}".format(aic_B))

Таким образом, у нас есть некоторые свидетельства того, что люди, ответившие на опрос, предпочитают продукт B продукту A.

Мы только что рассмотрели, как использовать метод оценки максимального правдоподобия в простом контексте обзоров товаров.

Одним из недостатков метода оценки максимального правдоподобия является невозможность включить наши предпосылочные убеждения о тех параметрах, которые мы оцениваем. Например, у большинства отзывов в основном либо 5 звезд, либо 1 звезда, и очень мало средних значений.

Как я говорил в предыдущей статье, мы можем рассматривать байесовский анализ данных как расширение оценки максимального правдоподобия, что может лучше подойти в практических ситуациях. Больше информации об оценке максимального правдоподобия можно найти в этой замечательной статье.

Материал подготовлен в рамках курса «Математика для Data Science». Если вам интересно узнать подробнее о формате обучения и программе, познакомиться с преподавателем курса — приглашаем на день открытых дверей онлайн. Регистрация здесь.