Классификация методом линейной дистилляции случайной сети / forpes.ru

12.11.2021 22:42

Igorglukhov 1 1900 Источник

Доброго времени суток! Меня зовут Игорь, работаю ad-hoc аналитиком в компании X5 Group и являюсь студентом Университета ИТМО. В данной статье будет предоставлен простой метод решения задачи классификации, основанный на линейных нейронных сетях и дистилляции знаний, конкурирующий по качеству с рядом базовых интерпретируемых моделей, а также с нелинейными сетями.

Введение

Одним из наиболее актуальных вопросов в области машинного обучения является интерпретируемость предоставляемых моделей. Для таких сложных моделей, какими являются ансамбли нескольких методов и глубокие нейронные сети, достаточно проблематично извлечь обоснование принятия решения в случае того или иного предсказания. Все более широкое применение машинного обучения в различных системах реального мира способствует увеличению потребности в четком понимании моделей. Разрабатываются различные методы, направленные на повышение интерпретируемости моделей, однако предлагаемые ими объяснения не до конца честны относительно того, как принимает решение исходная модель.

Вдобавок к этому, компромисс между качеством модели и ее интерпретируемостью имеет место быть далеко не всегда. В случае, когда данные хорошо структурированы и признаки выразительны, то значительной разницы между качеством ансамблей и качеством линейных моделей нет, соответственно, есть основания отдать предпочтение интерпретируемым моделям.

В данной работе представляется Метод Линейной Дистилляции – метод, основанный на линейных нейронных сетях, решающий задачу классификации. Он использует линейную функцию для каждого класса датасета, которые обучены моделировать выход некоторой учительской линейной функции для каждого класса отдельно. При этом учитель представляет из себя случайную линейную нейронную сеть - сеть, веса которой инициализированы случайным образом. После того, как модель обучена, мы можем осуществить классификацию путем определения «новизны» (Novelty Detection), опять же, для каждого класса. Данная модель выучивает монотонные зависимости между признаками и целевой меткой, что делает интерпретацию простой. Подобный метод ранее успешно использовался лишь в применении к задаче обучения с подкреплением.

Алгоритм классификации методом дистилляции случайной линейной нейронной сети

Дистилляция Один-ко-Многим

Метод дистилляции случайной нейронной сети использовался в задаче обучения с подкреплением для разведки в средах с разреженными наградами. В этом случае, дистилляция позволяет агенту определить какие состояния были посещены, а какие нет, и таким образом использовать любопытство для эксплорации. Пусть – множество наблюдаемых состояний. Предиктором мы будем называть сеть $\hat{f}:O\rightarrow\ \mathbb{R}^k$ , обученную предсказывать поведение таргета $f:O\rightarrow\ \mathbb{R}^k$ во время взаимодействия со средой, используя среднеквадратическую ошибку $||\hat{f}\left(x,\theta\right)-f\left(x\right)||^2$ для обновления весов предиктора $\theta_{\hat{f}}$ . Если разность между предсказанием случайной сети и предсказанием предиктора в некотором состоянии средывелика, то это означает высокий показатель любопытства и выдается большая награда. Это можно рассмотреть как модель обнаружения новизны, обучение которой проходит путем дистилляции случайной нейронной сети. Важным утверждением является то, что предиктор $\hat{f}$ может симулировать поведение таргетаесли их выразительная способность идентична. В данной работе это свойство выполнено путем удаления нелинейностей нейронных сетей и снижения их выразительности до линейной функции.

Рассмотрим задачу классификации с обучающим множеством $X\in\mathbb{R}^d$ , где метки объектов это множество $Y=\{1,\ldots,\ C\}$ , где – количество классов. Таким образом, мы имеем размеченный набор данных $D=\{x^i,\ y^i\}_{i=1}^n$ , где $x^i\in X,\ {\ y}^i\in Y$ . Предположим, что классификация выполняется некоторым метрическим классификатором (алгоритмом, использующим сходство объектов для получения итоговых меток класса) $A:\mathbb{R}^k\rightarrow Y$ , работающим с представлением объекта в пространстве размерности . Также рассмотрим таргет-функцию $Q_\phi:X\rightarrow\ \mathbb{R}^k$ , ставящую в соответствие объекты датасета в пространство размерности . Она может быть представлена линейной нейронной сетью или матрицей.

Идея заключается в создании линейных предикторов $P_{\theta_c}:X\rightarrow\ \mathbb{R}^k$ для каждого класса , которая будет симулировать поведение таргет-функции для заданного класса. Каждый предиктор обучен каждому объекту ${x}_c^i$ соответствующего класса ставить в соответствие представление таргет-функции $Q_\phi(x_c^i)$ .

Поскольку все функции из множества функций предикторов $\{{P_{\theta_c}}\}$ и таргет-функция $Q_\phi$ являются линейными, их можно представить в матричном виде. К примеру, $Q_\phi$ может рассматриваться как произведение матриц $W_LW_{L-1}\ldots W_1$ , где – натуральное число. Во время обучения, метки ${\ y}^i\in\{1,\ C\}$ используются для активации одного из предикторов $\{{P}_{\theta_c}\}$ Процесс обучения использует среднеквадратическую функцию потерь (2.1):

$L\left(P_{\theta_c}\right)=\ \frac{1}{N}\sum_{i=1}^{N}{(P_{\theta_c}x_c^i\ -\ W_LW_{L-1}\ldots W_1{\ x}_c^i)^2}\ .$

Во время оценивания модели предсказания осуществляются путем использования расстояния между каждым из выходов предикторов $P_{\theta_c}(x_c^i)$ и выходом таргет-функции $Q_\phi(x_c^i)$ . Финальное предсказание выбирается как ${argmin}_c\left(P_{\theta_c}{(x}_c^i)-\ Q_\phi(x_c^i)\right)^2$ .

Важно учесть, что несмотря на тот факт, что все предикторы линейны, их композиция не может быть выражена линейной функцией. Тем не менее, на каждом шаге обучения, учитель и таргет линейны.

Таким образом, мы заменили задачу классификации задачей аппроксимации линейной функции несколькими линейными функциями, связанными с каждым из классов. Данный метод называется Дистилляция Один-ко-Многим.

Дистилляция Многие-к-Одному

В прошлой главе был представлен подход к обучению линейных предикторов на выходах линейной таргет-функции. В этой главе, будет представлен подход к выбору этой функции.

Во-первых, поскольку предикторы симулируют выход таргета на соответствующих классах, когда мы сравниваем их выходы, мы можем точнее отличить один предиктор от другого, если класс сильно не похож на другие. К примеру, если выход таргета для класса 1 сильно отличается от его же выхода для других классов, то обученный предиктор, соответствующий классу 1, будет ближе к тагрету, чем остальные. Это будет возможно, если выходы таргета для каждого класса будут далеки друг от друга.

Один из способов выбрать $Q_\phi$ так, чтобы различным классам в соответствие ставились разные области в пространстве размерности выходного слоя – сделать это напрямую. К примеру, это можно сделать, обновляя параметры $\phi$ таргет-функции используя дистилляцию некоторого учителя.

В нашем случае, есть необычное свойство дистилляции: учитель не обязан обобщать данные. Будет достаточно того, чтобы учительская функция ставила разным классам в соответствие разные области выходного пространства. В отличие от стандартной парадигмы дистилляции, в данном методе учителем будет множество рандомизированных линейных функций $\{{P}_{\zeta_c}\}_{с=1}^С$ . Тогда мы сразу по умолчанию получаем различные выходные представления для каждого класса. Во время обучения, для каждого объекта мы выбираем линейную нейронную сеть из $\{{P}_{\zeta_c}\}_{с=1}^С$ согласно метке объекта y^i , после чего используем выбранное преобразование как таргет для $Q_\phi$ . Обучение производится путем минимизации следующей функции потерь (2.3):

$L\left(Q_\phi\right)=\ \frac{1}{N}\sum_{i=1}^{N}{(\ W_LW_{L-1}\ldots W_1{\ x}_c^i-\ P_{\zeta_c}x_c^i)^2}\$

Данный метод называется Дистилляция Многие-к-Одному. Точность предсказаний модели, обученная таким образом, неоптимальна. Одной из причин для этого является тот факт, что распределение, которое возвращают учителя, нелинейно. Поэтому у линейной таргет-функции возникают проблемы с выучиванием данного распределения.

Двунаправленная Дистилляция

В предыдущих главах были предложены модели Дистилляция Один-ко-Многим и Дистилляция Многие-к-Одному. В данной главе эти две идеи комбинируются в метод, называемый Двунаправленная Дистилляция.

После инициализации наши предикторы $\{{P}_{\theta_c}\}$ идентичны $\{{P}_{\zeta_c}\}$ , поэтому на первом шаге мы предобучаем функцию $Q_\phi$ на выходы $\{{P}_{\theta_c}\}_{с=1}^С$ в манере Дистилляции Многие-к-Одному, после чего дистиллируем знания назад в предикторы в манере Дистилляции Один-ко-Многим.

Процедура обучения представлена на рисунке 1. Во время Двунаправленной Дистилляции мы переключаемся между моделями Дистилляция Один-ко-Многим и моделью Дистилляция Многие-к-Одному в различных пропорциях, обучая их определенное количество итераций, позволяя всем параметрам быть обновленными несколько раз каждую эпоху. Красным отмечены таргет-функция, представленная линейной нейронной сетью и активированный предиктор, соответствующий поступившему на вход объекту класса 2.

Рис 1 - Архитектура модели Двунаправленная Дистилляция

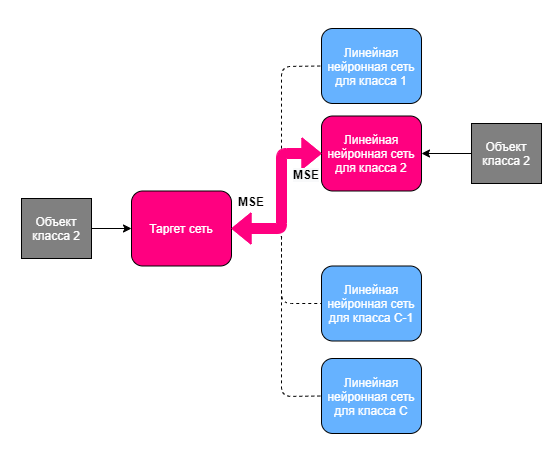
Эксперименты

В данной главе описываются результаты экспериментов, в которых сравнивались модели Дистилляция Один-ко-Многим и Двунаправленная Дистилляция с такими широкоиспользуемыми моделями, как полносвязный персептрон, логистическая регрессия, решающее дерево.

Все эксперименты проведены в парадигме Few-Shot Learning. Каждой модели подавалось размеченных объектов (называется “shot”) для каждого класса из . В отличие от стандартных Few-Shot моделей, наш метод не предполагает перевода знаний между эпизодами (полученными подмножествами размеченных объектов), что делает его похожим на small-sample learning. Во избежание смещения оценки, связанного с маленьким числом объектов в эпизоде, каждая модель обучалась на 100 независимых прогонах поэпох, после чего возвращалось среднее значение доли верно классифицированных объектов.

Эксперименты проводились на датасетах MNIST, Fashion-MNIST, OMNIGLOT, SVHN. Дополнительно к перечисленным датасетам изобрежаний, были проведены исследования на двух табличных наборах данных: Customer Churn и Covertype.

MNIST

Датасет MNIST – это набор изображений рукописных цифр от 0 до 9. Каждое изображение черно-белое, размер изображения – 28x28 пикселей. При тестировании моделей на данном датасете, картинки дополнительно не обрабатывались и аугментации данных не производилось. Оценки качества производились для моделей с шагами обучения $1e-3,\ 1e-4,\ 5e-5$ . Число эпох поддерживалось достаточно низким – не более 10 эпох, поскольку большее их количество приводило к переобучению. Дополнительно сравнивались статистики со следующими моделями: логистической регрессией, многослойным персептроном и наивной моделью. Наивной моделью мы называем алгоритм, в которой предикторы обучены без таргета - каждый предиктор обучен выводить представление, наиболее близкое ко входному вектору. На этапе предсказывания, класс выбирается измерением расстояния между выходом каждого предиктора и объектом x^i . Для многослойного персептрона исполозовались конфигурации с одним или двумя скрытыми слоями размеров 64, 254 и 1024.

В результат заносились наилучшие значения метрики, полученные для одной из конфигураций гиперпараметров модели. Результаты сравнения приведены в таблице 1. В каждой ячейке представлено значение доли верно классифицированных объектов. Видно, что с увеличением размера датасета, результат становится все лучше, но уже на датасетах размером в около тысячу объектов обучение значительно замедляется.

Таблица 1 - Результаты сравнения на датасете MNIST

Shot size	Дистилляция ОкМ	Двунапр. дистилляция	Лог. регрессия	Многосл. персептрон	Наивная модель
1	0.426	0.436	0.316	0.448	0.127
10	0.801	0.800	0.679	0.749	0.777
50	0.912	0.917	0.839	0.881	0.903
100	0.934	0.871	0.870	0.926	0.898
200	0.953	0.953	0.892	0.929	0.942

По результатам экспериментов над датасетом MNIST, виден явный прирост качества моделей над логистической регрессией и многослойным персептроном. При этом качество, достигаемое нелинейной нейронной сетью, было достигнуто дистилляционными методами на датасете меньшего размера.

Важным свойством нашей архитектуры является тот факт, что на малом количестве объектов они обучаются достаточно быстро. Сходимость каждой сети-студента к сети-учителю показано на рисунке 2.

Рис 2 - Кривые функции потерь для модели Двунаправленной Дистилляции. Модели обучены 10 эпох с 5 объектами на каждый класс

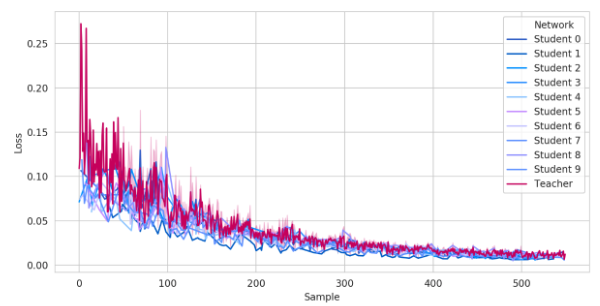
Обучение моделей Двунаправленной Дистилляции и Дистилляции Один-ко-Многим имеет преимущество над классической полносвязной сетью во время обучения на малом количестве данных. Двунапрвленная модель позволяет достичь гораздо более быстрой сходимости к наилучшему достигаемому качеству модели уже после первых эпох, поскольку таргет-сеть, предобученная на предикторах облегчает обучение. Сравнение процесса обучения моделей Дистилляции и полносвязного персептрона с двумя скрытыми слоями представлено на рисунке 3. По оси абсцисс представлено количество объектов обучения, которые сеть видела. По оси ординат показано значение исследуемой метрики на тестовом наборе данным, соответствующее количеству объектов, на которых модель обучалась.

Рис 3 - Кривые метрики «Доля верно классифицированных объектов» для моделей Двунаправленной Дистилляции, Дистилляции Один-ко-Многим, Полносвязного Персептрона. Модели обучены 10 эпох с 1, 5, 10 объектами на каждый класс в эпохе

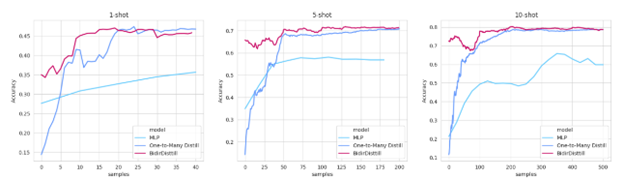
FMNIST, SVHN, Customer Churn, Covertype

Результаты для датасетов Fashion-MNIST, SVHN, а также для табличных наборов данных Customer Churn (датасет IBM оттока сотрудников) и Covertype (прогнозирование типа лесного покрова) представлены ниже.

Таблица 2 - Результаты сравнения на датасете Fashion-MNIST

Shot	Дистилляция ОкМ	Двунапр. дистилляция	Лог. регрессия	Многосл. персептрон	Решающее дерево
10	0.700	0.708	0.618	0.536	0.553
50	0.779	0.802	0.708	0.706	0.653
100	0.804	0.830	0.768	0.754	0.698
200	0.837	0.836	0.781	0.776	0.723
300	0.855	0.848	0.790	0.819	0.734

Как и в случае с датасетом MNIST, можно наблюдать улучшение исследуемой метрики. Для достижения значения метрики 0.8, дистилляционным подходам понадобился датасет с 50 объектами на класс, в то время как остальным моделям требуется не менее 300.

Таблица 3 - Результаты сравнения на датасете SVHN

Shot	Дистилляция ОкМ	Двунапр. дистилляция	Лог. регрессия	Многосл. персептрон	Решающее дерево
10	0.258	0.250	0.112	0.109	0.139
50	0.279	0.417	0.127	0.123	0.167
100	0.464	0.412	0.130	0.114	0.214
300	0.482	0.362	0.130	0.128	0.298

В силу того, что в данном датасете использовались цветные картинки, большинство моделей не смогли побить порог даже в 0.2, а дистилляционные методы не смогли превысить порог в 50% верно классифицированных объектов. Тем не менее, виден прирост метрики по сравнению со стандартными широко используемыми моделями.

Таблица 4 - Результаты сравнения на датасете Customer Churn

Shot	Дистилляция ОкМ	Двунапр. дистилляция	Лог. регрессия	Многосл. персептрон	Решающее дерево
10	0.69	0.68	0.56	0.63	0.68
50	0.66	0.68	0.67	0.74	0.74
100	0.73	0.68	0.67	0.76	0.76
200	0.74	0.69	0.74	0.80	0.76
300	0.74	0.76	0.69	0.82	0.75

Несмотря на тот факт, что в большинстве экспериментов наилучшие результаты показал многослойный персептрон, при обучении на небольшом количестве данных дистилляционные подходы сходятся к своему наилучшему достигаемому качеству быстрее, чем аналоги, показывая при этом сопоставимое качество.

Таблица 5 - Результаты сравнения на датасете Covertype

Shot	Дистилляция ОкМ	Двунапр. дистилляция	Лог. регрессия	Многосл. персептрон	Решающее дерево
10	0.49	0.48	0.23	0.45	0.54
50	0.60	0.56	0.43	0.64	0.60
100	0.61	0.63	0.56	0.64	0.65
200	0.63	0.63	0.62	0.67	0.68
300	0.63	0.63	0.60	0.69	0.70

В случае с данным датасетом, видим примерно похожие результаты по метрике качества, при этом решающее дерево в среднем показывает наилучшие результаты, что, скорее всего, связано с низкой размерностью входной матрицы данных.

Заключение

В данной работе была предоставлена архитектура модели искусственного интеллекта, основанная на подходах к решению задачи классификации, использующих дистилляцию случайной функции и линейные нейронные сети. Первый метод представлял собой обучение линейной нейронной сети моделировать выход некоторой учительской нейронной сети, при этом каждому классу соответствует собственная линейная функция. Второй метод использовал обучение одной линейной сети предсказывать выход множества линейных нейронных сетей, каждая из которых соответствует одному классу. Мотивацией служило создание такой архитектуры, состоящей из линейных функций, которая будет способна решать задачу классификации на небольшом наборе данных. Поскольку в методе отсутствует нелинейность, предложенный подход позволяет понять почему было сделано то или иное предсказание.

Эксперименты над моделями проводились на нескольких различных наборах изображений, а именно MNIST, FASHION-MNIST, SVHN. Дистилляционные подходы позволили получить модели, показывающие лучшие результаты, чем широкоиспользуемые нелинейные модели, на небольшом количестве данных.

Комментарии (1)

VPryadchenko
13.11.2021 12:58
#23701843
+2
Наверняка здесь скрывается какая-то интересная идея, но стиль изложения не позволяет ее сходу оценить. По тексту возникает много вопросов, в частности, по первой главе: какой смысл аппроксимировать линейную функцию линейными функциями? В чем смысл представлять последнюю в виде произведения L матриц? Не похоже, чтобы эта факторизация как-то использовалась. И т.д.

Классификация методом линейной дистилляции случайной сети +3