Приветствую Вас, уважаемые Читатели! Я уверен, что многие из Вас из школьного курса математики прекрасно помнят чудесную функцию - экспоненту, производная которой, сколько бы её не брать, равняется исходной функции.

Однако, многие ли из Вас знают, почему так происходит? Сегодня я хочу это рассказать на максимально простом языке. Поехали! Рассмотрим две показательные функции:

Вспомним теперь классическое определение производной функции как предела отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю.
Простыми словами: мы анализируем скорость изменения функции f(x) при бесконечно малом изменении её аргумента, которое мы будем обозначать ∆х.
В формулах для первой функции это выглядит так:

Давайте кое-что посчитаем на калькуляторе, а именно выражение под знаком предела. Например, пусть изменение функции ∆х = 0,001. Тогда:

Впрочем, это ничего нам не даст... До того момента, как мы не посчитаем аналогичное выражение для функции, в основании которой 3:

А вот это уже интересно. Если немного вспомнить математический анализ, то в голове всплывает вторая теорема Больцано-Коши или теорема о промежуточном значении.

Применительно к нашему случаю она позволяет утверждать, что рассматриваемая функция (имеется ввиду дробь (x^∆х-1)/∆х) при каком-то x равняется единице! Если мы найдем такое х, то по определению получим равенство функции её производной! Начинаем! Приравниваем нашу функцию к единице:
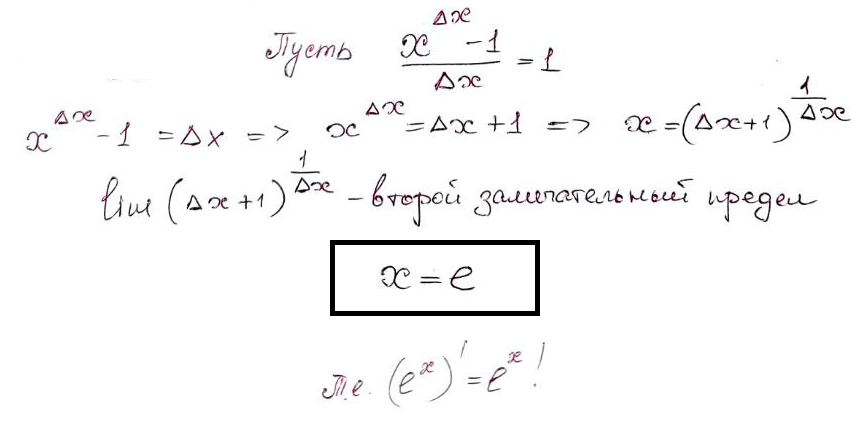
Второй замечательный предел - это известное из школьного курса соотношение, неизменно приводящее к числу Эйлера. Таким образом, доказательство окончено!
TELEGRAM "Математика не для всех" - там я публикую не только интересные статьи, но и математический юмор и многое другое.
Комментарии (32)

631052
27.11.2021 16:41+1так нам надо не чтоб дробь была равна 1, а предел дроби был равен 1.
нет я не оспариваю исходного утверждения, это я придираюсь (в математике так принято)
восклицательный знак в конце я бы не ставил. а то мне за ним начинает мерещиться гамма-функция, зачем нам всё это. ну ладно, моя личная заморочка.
ну а эллипс в школе учили рисовать двумя канцелярскими кнопкам и ниткой. используя определение эллипса как ГМТ, для которых сумма расстояний (и т.д. и т.п)
ну да, подписался на канал есть такое

GospodinKolhoznik
27.11.2021 17:00+11Как-то несолидно вести математический канал, и не владеть LaTeXом.

youngmysteriouslight
27.11.2021 17:30Вкусовщина. Мне это напомнило презентации и проходные статьи прошлого века, когда большая часть текста печаталась, а формулы вписывались вручную. Впрочем, я те времена вживую не застал, но материалы-то живы ещё.
P.S. в discord есть боты, которые парсят tex-вставки в сообщениях пользователей и сразу рендерят их в виде картинок. А как автор ведёт свой канал без подобного?

andreybrylb Автор
28.11.2021 15:19А мне нравится писать) пачка бумаги и в бой) обработка стандартным приложением xiaomi как документа

vectorplus
27.11.2021 17:57+7Я нежно люблю LaTeX, всегда им пользуюсь, и при прочтении статьи была такая же мысль. Но, тем не менее, мне эти записи на бумажке показались уютными и ламповыми, вызвали положительные эмоции. Кто из нас не писал формулы на обороте конверта, когда припекло? Тем и прекрасна математика, что суть можно хоть на банановой кожуре выразить.

vvadzim
27.11.2021 18:06+15Гхм.. ну как бы потому что экспонента это одно из решений простейшего дифференциального уравнения f(x)=f'(x). Правильно решили значит, чё....
А ещё дырочки в шкурке у кошки именно там где у кошки глазки.

Shkaff
28.11.2021 13:24одно из решений
Любопытно, но это единственное решение этого уравнения (с точностью до константы). Нет других функций, которые были бы производными самих себя.

GospodinKolhoznik
28.11.2021 20:59+1

Shkaff
28.11.2021 21:15с точностью до константы;) В вашем случае константа = 0.

haqreu
29.11.2021 01:22Я привык к употреблению словосочетания "с точностью до константы" в значении добавления константы. Вы же употребляете в смысле "с точностью до умножения на константу", что для меня необычно. А для вас?

Shkaff
29.11.2021 11:16Ну да, я мог бы написать и попонятнее, my bad, но с добавлением константы оно не работает, так что мне и в голову не пришло.

muxa_ru
27.11.2021 18:28+14Почему производная экспоненты равна ей самой?
ПО ОПРЕДЕЛЕНИЮ экспоненты, потому что неперово число является результатом решения уравнения в котором степенная функция равна производной от себя.
Точно так же можно задавать вопрос "почему функция икс_в_квадрате равна функции икс_умножить_на_икс". Ответом тоже будет "по определению".

haqreu
28.11.2021 13:40+1Только определение не уникально; правильнее было бы сказать "по одному из определений". Лично мне экспоненциальную функцию вводили как предел lim (1+x/n)^n.
Впрочем, у нас преподаватель анализа был оригинален, и даже производную определял как коэффициент второго члена ряда Тейлора функции в точке.

631052
28.11.2021 17:56+1вот да об чем и речь. по одному из определений.
вот если бы автор доказал, что они эквивалентны, то было бы неплохо.
т.е. сначала для последовательности: она возрастает, ограничена сверху, значит есть предел. обзовем его "е".
и пусть докажет, что показательная функция e^x с таким вот "е" (введенным как предел последовательности) обладает заявленным свойством.

yukon39
27.11.2021 18:32+11Почему производная экспоненты равна ей самой?
Это вы её еще интегрировать не пробовали!

maisvendoo
27.11.2021 19:05+4Сдается мне, что ответ на вопрос поста прост как 5 копеек - данная функция может быть определена как частное решение дифференциального уравнения
y'(x) = y(x)откуда и следует ответ, очевидный из уравнения

maggg
27.11.2021 20:47+6Не обижайтесь только, но вы только что доказали, что отношение длины окружности к диаметру равно pi, воспользовавшись школьной формулой для длины окружности. Но это не доказательство, а тавтология.

maisvendoo
27.11.2021 22:23+5Анекдот на тему.
Попал студент в психушку. Новенький, его бывалые пациенты обступили, смотрят, трогают, в общем достали. Ему надоело, и он рыкнул:
- Сейчас я вас всех продифференцирую!
Половина смылась. Он ещё раз:
- Сейчас я вас всех проинтегрирую!
Смылась другая половина. Остался один псих. Студент ему:
- А ты, что, меня не боишься!?
- А я - e в степени икс!

Alexander_The_Great
29.11.2021 02:18+1Как вообще модераторы такое пропускают? В последнее время всё больше околонаучных статей на хабре либо не имеют отношения к науке, либо пишутся фриками.

sargon5000
29.11.2021 04:17+2Камрад, плюньте вы на математику и займитесь русским языком, с ним у вас серьезные проблемы. Когда я читаю ваше "многие из Вас ...' – у меня кровь из глаз течёт. Запомните, "вы" и "вас" никогда не пишутся с большой буквы при обращении к нескольким людям сразу. Скажу больше: писать "Вы" и при обращении к одному лицу не нужно почти никогда. Нужно всего в трёх случаях, поинтересуйтесь сами, в каких. Когда вы обращаетесь к единственному человеку так, как будто его здесь несколько, то есть на "вы" – это уже абсолютно достаточное проявление вежливости!

VladimirLadynev
30.11.2021 04:59Я не сильно разбираюсь в математике. И вот что меня смутило (x^∆х-1)/∆х) — здесь x, это не тот же самый x, что в 2^x или 3^x. Может быть его другой буквой лучше обозначить: (a^∆х-1)/∆х). Или я не прав?


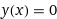


ashiku
И почему производная экспоненты равна 0?
Вы ведь сами показали, что в случае, например, f(x) = 2^x производная равна log2(e) * 2^x, что не равно нулю собственно говоря нигде.
Простите за токсичность, но название вашего канала играет новыми красками :)
andreybrylb Автор
Да я попутал))) ей самой конечно)