Обзор архитектуры AlphaFold 2 / forpes.ru

Главная
Обзор архитектуры AlphaFold 2

Обзор архитектуры AlphaFold 2 +52

29.11.2021 14:13

boygenius 2 2600 Источник

В данном обзоре мы подробно рассмотрим нейронную сеть AlphaFold 2 от компании DeepMind, с помощью которой недавно был совершен прорыв в одной из важных задач биологии и медицины: определении трехмерной структуры белка по его аминокислотной последовательности.

В первых трех разделах обзора описывается задача, формат входных данных и общая архитектура AlphaFold 2. Далее, начиная с раздела «Input feature embeddings», описываются детали архитектуры. В разделе «Резюме» кратко суммируется основная информация из обзора.

В научной статье, опубликованной в Nature, и дополнительных материалах к ней, авторы используют название «AlphaFold» без цифры 2, и мы также будем его придерживаться.

Белки и их структуры

Белки – это органические молекулы, структура которых показана на рис. 1. Символом R обозначены аминокислотные остатки, которые могут быть 20 разных типов. Таким образом, белок можно закодировать строкой, записанной алфавитом из 20 символов.

Белки сворачиваются в структуру за счет различных взаимодействий между атомами (водородные связи, ковалентные связи и др.). Структура белка определяется его аминокислотной последовательностью и, в свою очередь, определяет свойства этого белка в живом организме.

Задача, которую решает AlphaFold, заключается в предсказании структуры белка по его аминокислотной последовательности. Экспериментальное определение структуры белков является очень трудоемким. Решение этой задачи с помощью физического моделирования требует огромных вычислительных ресурсов. Проблема усугубляется тем, что в процессе сворачивания белка часто участвуют другие белки.

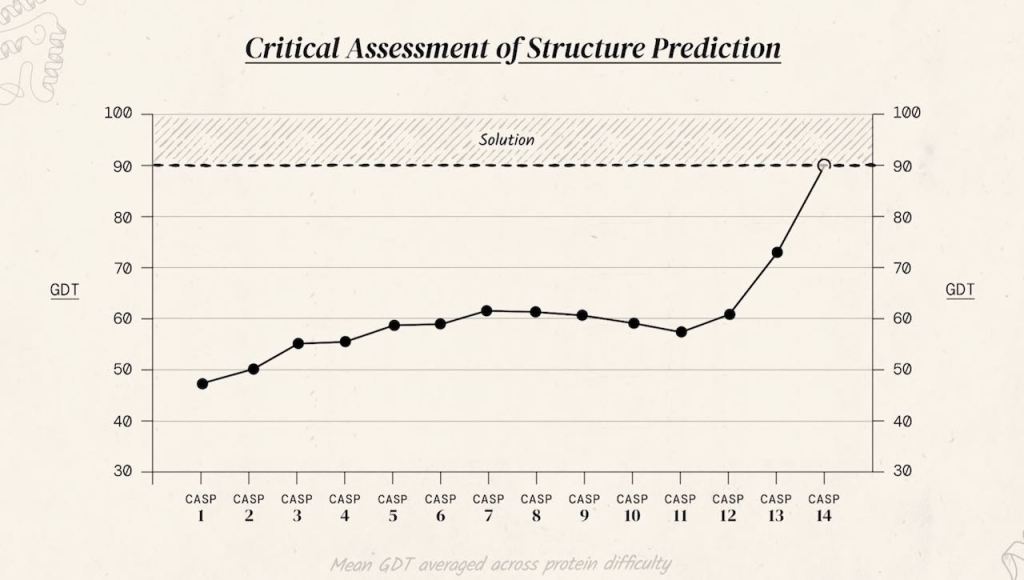
Каждые 2 года организуется соревнование CASP (Critical Assessment of protein Structure Prediction), в котором научные группы соревнуются в точности предсказания структур белков. Для оценки точности каждый раз используется новый набор белков, структуры которых уже были получены экспериментально, но еще не были опубликованы.

В 2020 году DeepMind с их нейронной сетью AlphaFold 2 выиграла соревнование CASP14, достигнув беспрецедентного уровня точности (рис. 2). DeepMind также выложили на YouTube видео об этом историческом успехе, которое рекомендую посмотреть. Об архитектуре AlphaFold версии 2 и пойдет речь в этом обзоре.

Рис. 2. Максимальная точность по метрике GDT, достигнутая в ходе соревнований CASP в разные годы (1994-2020).

Предсказание структуры на основе эволюционного сходства

Аминокислотная последовательность белков меняется в процессе эволюции. Лишь часть аминокислот в цепочке влияет на структуру белка: мутации в этих местах скорее всего приведут к неправильному сворачиванию белка и утрате им своих полезных свойств. В результате организм с большой вероятностью отсеивается естественным отбором. Поэтому в ходе эволюции мутации в основном накапливаются в тех местах белка, которые не оказывают влияния на его структуру.

Если мы возьмем белок, выполняющий одну и ту же функцию в разных живых организмах, то увидим различия, накопившиеся в ходе эволюции от общего предка. Такое сопоставление называется множественным выравниванием последовательностей (multiple sequence alignment, MSA). Пример показан на рис. 3. Каждая строка – вид организма, столбец – код аминокислоты. Иногда в ходе эволюции аминокислоты могут удаляться или добавляться в белок. Чтобы было возможно выравнивание, удаленные аминокислоты в MSA обозначаются дефисом.

Например, мы видим, что аминокислота на позиции 22 (лизин, символ «K») одинакова у всех организмов в таблице, тогда как аминокислота на позиции 23 сильно варьируется. Это говорит о том, что аминокислота К в данной позиции важна для сохранения структуры белка.

Мутации в местах, определяющих структуру белка, не только редки, но обычно происходят «парами»: то есть сразу два аминокислотных остатка, которые находятся в контакте друг с другом, мутируют так, что контакт сохраняется, а значит сохраняется структура белка и его свойства (рис. 4). В результате организм получается жизнеспособным и не отсеивается естественным отбором.

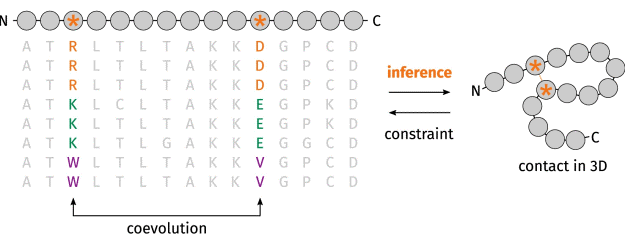
Таблицу MSA можно составить для любого белка, найдя в базе данных наиболее схожие и эволюционно близкие к нему белки. Коррелирующие элементы последовательности вероятно контактируют, часто меняющиеся – не влияют на структуру. Поэтому таблицу MSA можно использовать при предсказании трехмерной структуры белка. Более того, для многих белков уже известны трехмерные структуры. Если в MSA найдутся белки с известными структурами, то по их структуре можно попытаться восстановить структуру исследуемого белка.

Предварительная обработка данных

Формат входных данных

Белок, для которого требуется определить структуру, будем называть целевым белком. Его аминокислотная последовательность представлена в виде строки из символов. Для целевого белка выполняется поиск в базе данных и составляется таблица MSA. Также происходит поиск шаблонов (templates): нескольких наиболее похожих белков с известной структурой. Каждый шаблон представлен в виде координат атомов в пространстве. Как вариант, может не быть ни одного шаблона. Таким образом, входными данными являются:

Целевой белок
Таблица MSA
Шаблоны (опционально)

Целевой белок

Целевой белок состоит из последовательности аминокислотных остатков (residues), для которых нужно определить пространственные положения.

Для целевого белка выполняется one-hot кодирование (20 аминокислот + «неизвестно»). Таким образом, аминокислотная последовательность длиной превращается в массив $\text{target_feat}$ из нулей и единиц размером (N, 21) .

Обрезка целевого белка и таблицы MSA

По оси, соответствующей номеру аминокислоты, целевой белок и таблица MSA обрезаются до фиксированной длины (выбирается случайный участок таблицы). На разных этапах обучения AlphaFold размер вырезаемого участка равен 256 и 384.

Создается массив $\text{residue_index}$ , который хранит для целевого белка позиции аминокислот до обрезки. Например, если мы обрезали белок с 20 по 40 позицию, то массив $\text{residue_index}$ будет состоять из чисел [20, 21, …, 39].

Подробнее см. Supplementary Material, раздел 1.2.8

Примечание. Здесь остается вопрос: насколько точно можно предсказать структуру белка, если обрезать его часть? В работе я не нашел освещения этого вопроса, но точность AlphaFold говорит сама за себя. Мне удалось найти таблицу распределения белков по длинам аминокислотных последовательностей (рис. 5).

Рис. 5. Распределение белков по длинам аминокислотных последовательностей в базе данных PDB30.

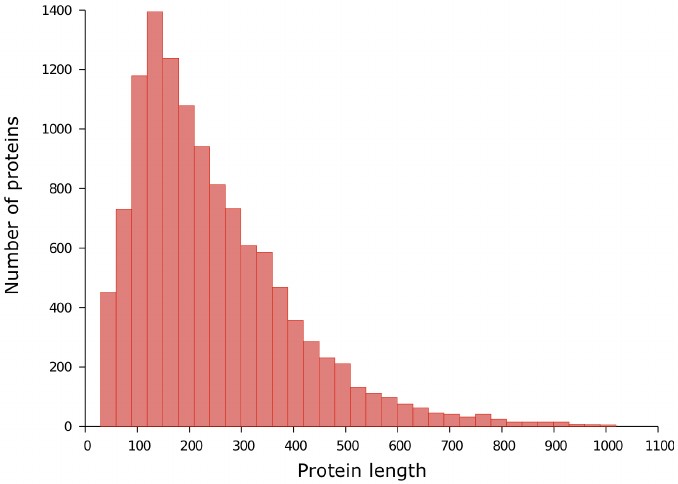
Кластеризация и маскирование таблицы MSA

Сложность вычислений и объем требуемой памяти в AlphaFold квадратично зависит от количества последовательностей в MSA, и лишь линейно от длины последовательности, поэтому количество последовательностей в MSA желательно уменьшить. Можно было бы выбирать случайную подвыборку последовательностей, но авторы предлагают другой подход: последовательности объединяются в кластеры.

В качестве метрики расстояния выбирается расстояние Хэмминга между последовательностями: число позиций, в которых аминокислоты различаются. Случайная подвыборка последовательностей выбирается в качестве центров кластеров, для всех остальных последовательностей ищется ближайший кластер.

Также 15% аминокислот в MSA «маскируется», то есть заменяется на случайную аминокислоту или на символ [MASK], для которого также выделяется бит в one-hot кодировании. Одна из задач сети AlphaFold 2 в ходе обучения состоит в том, чтобы предсказать замененные аминокислоты. Это работает аналогично задаче «masked language model» в языковой модели BERT.

Подробнее см. Supplementary Material, раздел 1.2.7

Если количество кластеров равно $N_{clust}$ , а длина последовательности равна $N_{res}$ , то данные собираются в массив $\text{msa_feat}$ размером ( $N_{clust}$ , $N_{res}$ , 49). Для каждого , вектор $\text{msa_feat}_{s, i}$ размерностью 49 является конкатенацией one-hot кодирования -й аминокислоты центра -го кластера, распределения по аминокислотам для всего -го кластера и некоторых дополнительных данных.

Таким образом, массив $\text{msa_feat}$ содержит информацию о таблице MSA, после кластеризации, маскирования и one-hot кодирования.

На этом, однако, сложности не заканчиваются. Создается еще один дополнительный массив $\text{extra_msa_feat}$ , состоящий из дополнительного набора последовательностей из MSA, не включенных в кластеры. Аминокислоты также кодируются one-hot кодированием, добавляются некоторые дополнительные данные. В результате массив $\text{extra_msa_feat}$ имеет размер ( $N_{\text{extra_seq}}$ , $N_{res}$ , 25).

Подробнее см. Supplementary Material, раздел 1.2.9

Данные о шаблонах

Исходными данными служат координаты атомов $\beta$ -углерода (или $\alpha$ -углерода для аминокислоты глицин) (рис. 6).

Рис. 6. Атомы alpha- и beta-углерода в молекуле белка.

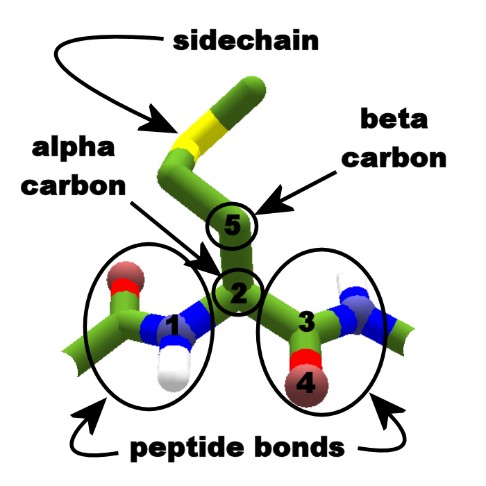
Создается массив попарных расстояний (авторы используют термин «дистограмма», англ. distogram) между атомами $\beta$ -углерода. Этот массив инвариантен к сдвигу, повороту и отражению системы координат. Далее выполняется дискретизация каждого расстояния между 3.25 Å и 50.75 Å с 39 возможными значениями (последнее значение – «50.75 Å или больше»). После дискретизации выполняется one-hot кодирование.

Массив $\text{template_pair_feat}$ состоит из полученной дистограммы и некоторых дополнительных данных. Этот массив имеет размер ( $N_{templ}$ , $N_{res}$ , $N_{res}$ , 88), где $N_{templ}$ – количество шаблонов.

Массив $\text{template_angle_feat}$ содержит информацию об аминокислотах, из которых состоят шаблоны, и об углах, под которыми соединены атомы в цепочке.

Подробнее см. Supplementary Material, раздел 1.2.9

Результаты обработки

В результате предварительной обработки данных мы получили 6 массивов. Их размеры и описания суммаризированы ниже.

$\text{target_feat}\ (N_{res}, 21)$ – данные об аминокислотах целевого белка
$\text{residue_index}\ (N_{res},)$ – данные о том, какую часть целевого белка мы обрезали
$\text{msa_feat}\ (N_{clust}, N_{res}, 49)$ – данные о кластеризованной таблице MSA
$\text{extra_msa_feat}\ (N_{\text{extra_seq}}, N_{res}, 25)$ – данные о дополнительных последовательностях в MSA
$\text{template_pair_feat}\ (N_{templ}, N_{res}, N_{res}, 88)$ – данные о шаблонах, в т. ч. попарные расстояния между атомами в каждом шаблоне
$\text{template_angle_feat}\ (N_{templ}, N_{res}, 51)$ – данные о шаблонах: аминокислоты и углы между атомами в каждом шаблоне

Архитектура AlphaFold

В этом разделе мы рассмотрим основные вычислительные блоки, из которых состоит архитектура AlphaFold версии 2. Рассмотрим назначение каждого блока и формат передаваемых между ними данных, но пока не будем детально рассматривать внутреннее устройство блоков.

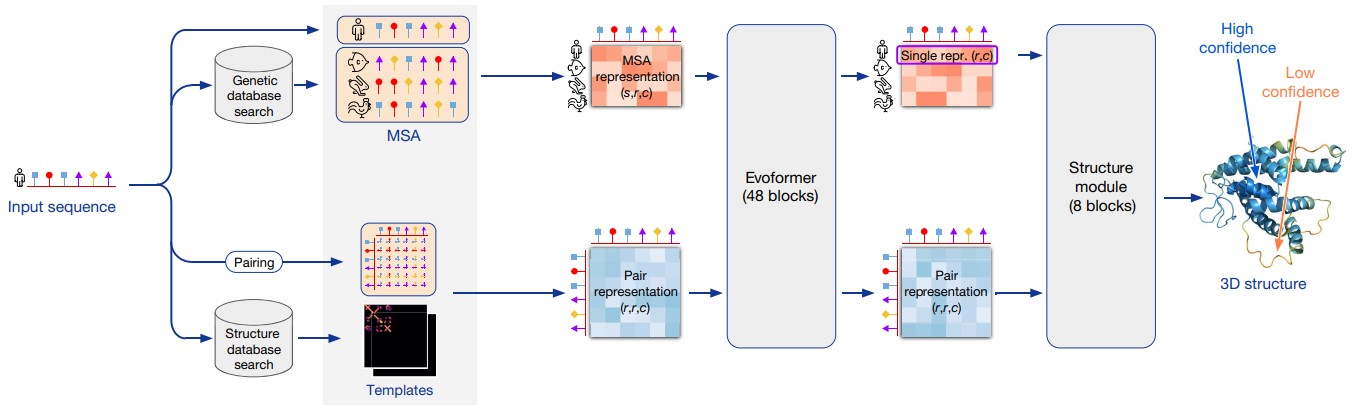
Модель AlphaFold способна выдавать ответ (трехмерную структуру белка) за один end-to-end запуск. Но авторы обнаружили, что можно улучшить качество предсказаний, запуская AlphaFold многократно (recycling iterations): каждую следующую итерацию модель использует выходные данные, полученные на предыдущей итерации, и обновляет предсказания. Это усложняет архитектуру, поэтому сначала рассмотрим более простой вариант без использования recycling iterations (Рис. 7).

Рис. 7. Упрощенный вариант AlphaFold без recycling iterations.

Input feature embeddings

Первый блок AlphaFold принимает на вход 6 массивов, которые мы получили в результате предварительной обработки данных. Этот блок выполняет последовательность операций с обучаемыми весами, и его выходными данными являются три массива:

MSA representation, размером $(N_{clust}, N_{res}, 256)$ . Вектора-эмбеддинги для каждой пары «позиция + номер кластера». Под «позицией» имеем в виду номер аминокислотного остатка.
Pair representation, размером $(N_{res}, N_{res}, 128)$ . Вектора-эмбеддинги для каждой пары позиций.
Extra MSA representation, размером $(N_{\text{extra_seq}}, N_{res}, 64)$ . Вектора-эмбеддинги для каждой пары «позиция + номер последовательности».

Это работает так же, как в задачах NLP (эмбеддинги слов). Входные данные, изначально представленные в понятном человеку формате, мы переводим в некий «внутренний формат», понятный только нейронной сети. Например, в массиве pair representation каждой паре позиций соответствует вектор размерностью 128.

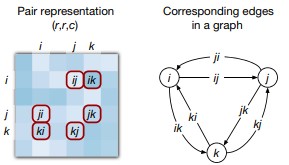
Элемент i, j массива pair representation является вектором-эмбеддингом пары позиций i, j , или, иначе говоря, эмбеддингом ориентированного ребра, связывающего позиции и (рис. 8). При этом считается, что между каждой парой позиций есть два ориентированных ребра (полносвязный граф).

Рис. 8. Элемент pair representation как эмбеддинг направленного ребра.

Evoformer stack

Evoformer-блок – это вычислительный блок с обучаемыми весами, разработанный для архитектуры AlphaFold. Этот блок принимает на вход массивы pair representation и MSA representation и возвращает два массива таких же размеров. Внутри Evoformer-блока происходит обмен информацией между массивами и их обновление.

В первых 4 evoformer-блоках осуществляется обмен информацией между pair representation и extra MSA representation. В следующих 48 блоках осуществляется обмен информацией между pair representation и MSA representation.

Внутреннее устройство evoformer-блока мы разберем позднее. Пока достаточно сказать, что Evoformer-блок близок к трансформеру (Vaswani et al. 2017) и использует механизм self-attention.

Именно с помощью evoformer-блоков AlphaFold определяет трехмерную структуру белка. Полученный на выходе обновленный массив pair representation теперь содержит информацию о трехмерной структуре, и задача следующего блока – извлечь эту информацию и построить саму структуру в явном виде.

Примечание. Для построения трехмерной структуры (с точностью до отражения) достаточно иметь матрицу попарных расстояний между позициями, то есть массив размером ( $N_{res}$ , $N_{res}$ ). Поскольку массив pair representation имеет в 128 раз больший размер, нейронной сети должно не составить труда закодировать в нем ту же информацию. Кроме того, в pair representation должна быть закодирована информация, позволяющая восстановить не только позиции атомов $\alpha$ -углерода, но и позиции все остальных атомов углерода и азота в молекуле белка, а также оценить уверенность в предсказаниях.

Еще одним выходом Evoformer stack является массив single representation: для этого каждый вектор первой строки массива MSA representation, полученного на выходе, обрабатывается полносвязным слоем. Смысл массива single representation в том, что он кодирует информацию о каждом остатке в отдельности, а не о каждой паре остатков.

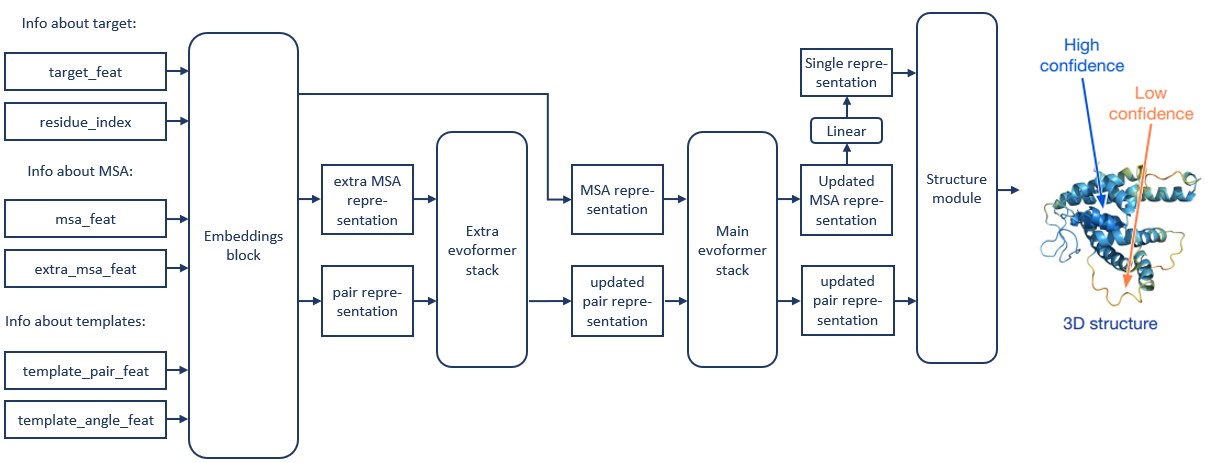
На схеме AlphaFold, которая была приведена выше, авторы для краткости не показали первые 4 evoformer-блока (extra evoformer stack). Более подробная схема показана рис. 9.

Рис. 9. Более детальная схема вычислений в упрощенном варианте AlphaFold без recycling iterations.

Structure module

После получения выходных данных evoformer stack работа с MSA-таблицей заканчивается. Блок structure module принимает на вход данные, полученные на выходе из evoformer stack:

single representation размером $(N_{res}, 384)$ – вектора-эмбеддинги для каждой позиции
pair representation размером $(N_{res}, N_{res}, 128)$ – вектора-эмбеддинги для каждой пары позиций

Предполагается, что в этих массивах уже закодирована информация о возможной структуре белка. Остается построить саму структуру. В задаче предсказания структуры белка выходные данные могут иметь разный формат, например:

Вариант 1. Координаты всех атомов белка. Систему координат можно выбрать произвольно, поэтому такое представление не единственно. Из-за этого не так просто подобрать подходящую функцию потерь.
Вариант 2. Массив попарных расстояний между атомами. Такое представление инвариантно к сдвигу и вращению системы координат, однако оно также инвариантно к отражению системы координат. Но два зеркально отраженных белка – это не одно и то же.
Вариант 3. Углы между всеми атомами в цепочке. Такое представление тоже инвариантно к отражению системы координат. Кроме того, оно неустойчиво: вся структура сильно меняется при небольших изменениях углов.

В AlphaFold 1 нейросеть предсказывала попарные расстояния и углы между атомами в цепочке. Координаты атомов затем вычислялись на основе этих данных градиентным спуском.

В AlphaFold 2 нейросеть напрямую предсказывает координаты атомов, а также оценивает уверенность в предсказаниях. В качестве основной функции потерь используется Frame Aligned Point Error (FAPE). Эта функция инвариантна к смене системы координат как в предсказанных, так и в эталонных данных.

Более детально блок Structure module и функцию потерь FAPE мы будем рассматривать в соответствующем разделе.

Recycling

В общем виде механизм recycling может быть применен к моделям, которые способны уточнять приблизительный ответ, используя дополнительные данные, то есть к моделям следующего вида:

$\text{output} = \text{Model}(\text{input}, \text{output}_{\text{prev}})$

Инференс с recycling заключается в инициализации ответа нулями и запуске модели выбранное число ( $N_{cycle}$ ) раз, используя входные данные и предыдущий ответ.

Recycling рассматривается лишь как дополнительный механизм, повышающий точность, поэтому мы хотели бы, чтобы даже после первой итерации модель выдавала бы ответ с хорошей точностью. В качестве функции потерь можно выбрать среднее значение ошибки по всем итерациям:

$\cfrac{1}{ N_{cycle}}\sum\limits_{c=1}^{N_{cycle}} \text{loss}(\text{outputs}_c)$

Если модель дифференцируема, то такую функцию потерь можно минимизировать напрямую. Однако это приведет к существенному перерасходу памяти и времени вычислений, по сравнению с однократным запуском модели. Авторы предлагают другой подход: на каждом шаге обучения выбирается случайное число между 1 и $N_{cycle}$ (общее для всех примеров в батче), модель запускается раз, и градиент ошибки распространяется только по последней итерации.

Подробнее см. Supplementary Material, раздел 1.10

Применение recycling в AlphaFold

AlphaFold использует в качестве входных данных шаблоны, то есть трехмерные структуры эволюционно схожих белков. Эти шаблоны играют роль гипотез о том, какой может быть структура белка. Выходными данными также является трехмерная структура, поэтому к AlphaFold может быть применен механизм recycling (рис. 10). Для этого блок input feature embeddings должен быть модифицирован таким образом, чтобы использовать не только 6 входных массивов данных, но и выходные и промежуточные данные, полученные на предыдущей итерации:

Single representation (первая строка массива updated MSA representation)
Updated pair representation
3D structure

На первой итерации эти значения инициализируются нулями.

Рис. 10. Общая схема AlphaFold с recycling iterations.

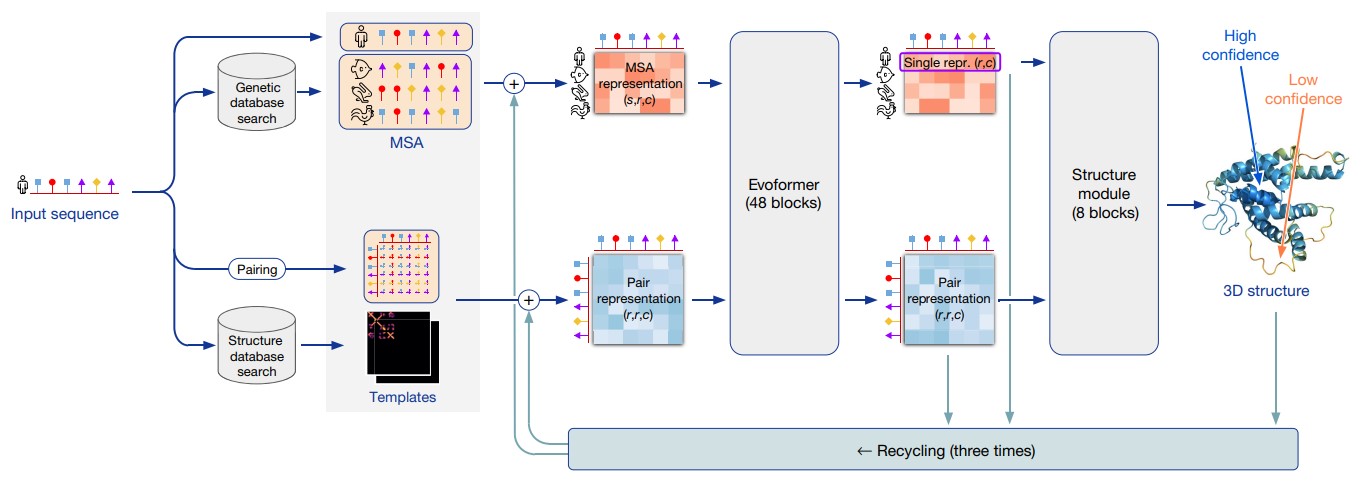
Авторы экспериментально подтверждают, что добавление механизма recycling в AlphaFold улучшает точность предсказаний – особенно это проявляется на тех белках, для которых таблица MSA содержит недостаточно информации.

Еще одна (несущественная) деталь заключается в том, что во время инференса evoformer stack запускается параллельно 3 раза на разных подвыборках таблицы MSA, и полученные выходные данные усредняются.

См. также Supplementary Material, Algorithm 2

Теперь начнем подробное рассмотрение каждого блока архитектуры.

Input feature embeddings

Блок Input feature embeddings (рис. 11) принимает на вход следующий набор данных:

Массивы, полученные в результате предварительной обработки данных:
1. $\text{target_feat}\ (N_{res}, 21)$ – данные об аминокислотах целевого белка.
2. $\text{residue_index}\ (N_{res},)$ – данные о том, какую часть целевого белка мы обрезали.
3. $\text{msa_feat}\ (N_{clust}, N_{res}, 49)$ – данные о кластеризованной таблице MSA.
4. $\text{extra_msa_feat}\ (N_{\text{extra_seq}}, N_{res}, 25)$ – данные о дополнительных последовательностях в MSA.
5. $\text{template_pair_feat}\ (N_{templ}, N_{res}, N_{res}, 88)$ – данные о шаблонах, в т. ч. попарные расстояния между атомами в каждом шаблоне.
6. $\text{template_angle_feat}\ (N_{templ}, N_{res}, 51)$ – данные о шаблонах: аминокислоты и углы между атомами в каждом шаблоне.
Данные с предыдущей итерации (recycling), которые на первой итерации заменяются массивами из нулей:
1. $\text{single_representation}\ (N_{res}, 384)$ – массив внутренних представлений (эмбеддингов) для каждой позиции.
2. $\text{pair_representation}\ (N_{res}, N_{res}, 128)$ – массив внутренних представлений (эмбеддингов) для каждой пары позиций.
3. $x\ (N_{res}, 3)$ – координаты атомов $\beta$ -углерода (или $\alpha$ -углерода для глицина) в предсказанной моделью трехмерной структуре (см. также раздел «данные о шаблонах»).

Рис. 11. Схема блока Input feature embeddings. Примечание: данные, полученные с предыдущей итерации, здесь не отображены; они используются в блоках «R» на данной схеме.

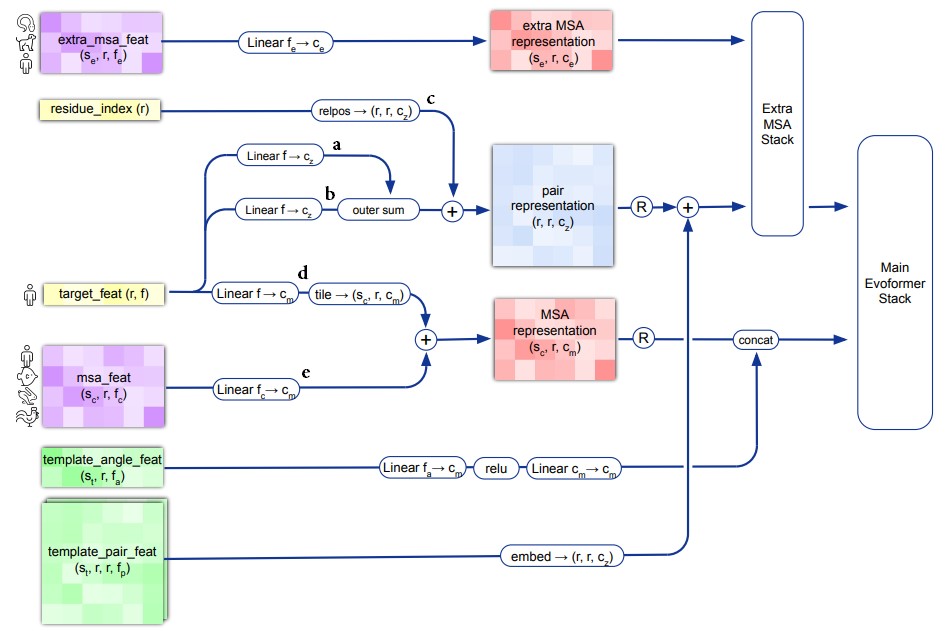
Общий смысл всех выполняемых действий в том, что информация, относящаяся по смыслу к одной позиции, идет в MSA representation, а информация, относящаяся по смыслу к паре позиций, идет в pair representation. Таким образом, в MSA representation собирается вся доступная информация о позициях, а в pair representation собирается вся доступная информация о парах позиций.

Pair representation

Начнем с того, как $\text{target_feat}$ и $\text{residue_index}$ преобразуются в $\text{pair representation}$ . $\text{target_feat}$ - это последовательность векторов, соответствующих позициям в целевом белке. Каждый вектор состоит из нулей и только одной единицы (one-hot кодирование). Слой $\text{Linear} f \to c_z$ переводит каждый вектор из исходной размерности в размерность c_z = 128 . Применяя два таких слоя, мы получаем массивы и .

Обработка вектора, полученного one-hot кодированием, с помощью полносвязного слоя – это то же самое, что слой Embedding в NLP-архитектурах. То есть каждой аминокислоте сопоставляется обучаемый вектор.

Чтобы получить pair representation, мы выполняем внешнюю сумму двух последовательностей векторов:

$\text{pair representation}_{i, j} = a_i + b_j$

Далее с помощью массива $\text{residue_index}$ мы должны выполнить позиционное кодирование (как в трансформере). Для этого создается обучаемый вектор-эмбеддинг для чисел ${-32, -31, \dots, 32}$ (всего 65 векторов). Вектор $c_{i, j}$ рассчитывается следующим образом: ищется число из множества ${-32, -31, \dots, 32}$ , ближайшее к i - j , и в качестве $c_{i, j}$ подставляется вектор-эмбеддинг, соответствующий этому числу.

Таким образом, в позиционном кодировании стираются различия между всеми расстояниями меньше -32 и больше 32. Авторы комментируют это так:

Since we are clipping by the maximum value 32, any larger distances within the residue chain will not be distinguished by this feature. This inductive bias de-emphasizes primary sequence distances. Compared to the more traditional approach of encoding positions in the frequency space [Vaswani et al. 2017], this relative encoding scheme empirically allows the network to be evaluated without quality degradation on much longer sequences than it was trained on.

Полученные вектора позиционного кодирования прибавляются к $\text{pair representation}_{i, j}$ .

MSA representation

Для получения MSA representation мы используем $\text{target_feat}$ и набор MSA-кластеров $\text{msa_feat}$ .

Аналогично, каждый вектор $\text{target_feat}$ и каждый вектор $\text{msa_feat}$ обрабатываются полносвязными слоями, получая массивы и . Однако массив получается двухмерный, а массив трехмерный. Мы добавляем к массиву новую ось, повторяя его столько раз, сколько было кластеров в MSA. Затем складываем полученные массивы.

Extra MSA representation мы получаем аналогичным способом, но уже без участия $\text{target_feat}$ .

Подробнее см. Supplementary Material, раздел 1.5

Использование информации о шаблонах

Каждый вектор в $\text{template_angle_feat}$ , который содержит данные о шаблонах и углах в них, обрабатывается нейронной сетью со скрытым слоем (Linear-ReLU-Linear) для получения вектора-эмбеддинга, и полученный эмбеддинг конкатенируется с MSA representation.

Каждый вектор в $\text{template_pair_feat}$ , обрабатывается полносвязным слоем для получения эмбеддинга (рис. 8, слой «embed»). Далее этот эмбеддинг обрабатывается цепочкой операций, которые не отражены на рис. 8, а именно:

Triangular self-attention around starting node
Triangular self-attention around ending node
Triangular multiplicative update using outgoing edges
Triangular multiplicative update using incoming edges
Pair transition

Эти же операции применяются в evoformer-блоках, поэтому мы будем разбирать их позднее, при описании evoformer-блока. После применения этих операций мы получаем массив размером ( $N_{templ}$ , $N_{res}$ , $N_{res}$ , 128) – эмбеддинг каждой пары позиций в каждом шаблоне.

Затем мы добавляем эту информацию к pair representation, используя механизм template pointwise attention. Это вариант multi-head self-attention (Vaswani et al. 2017), в котором запросом (query) является -й элемент pair representation, а ключами и значениями - -е элементы каждого из шаблонов. Более детально останавливаться на этой операции сейчас не будем.

Подробнее см. Supplementary Material, раздел 1.7.1

Также в блоках «R» (recycling) мы используем информацию с предыдущей итерации. Для экономии места также не будем разбирать принцип работы блока «R», поскольку он является лишь дополнительным инструментом.

Подробнее см. Supplementary Material, раздел 1.10

Evoformer

Блок evoformer принимает и возвращает два массива:

MSA representation, размером $(N_{clust}, N_{res}, 256)$ – эмбеддинги пар (позиция + последовательность).
Pair representation, размером $(N_{res}, N_{res}, 128)$ – эмбеддинги пар (позиция + позиция)

И устроен из блоков, имеющих собственные обучаемые веса (рис. 12).

Рис. 12. Схема вычислений в evoformer-блоке.

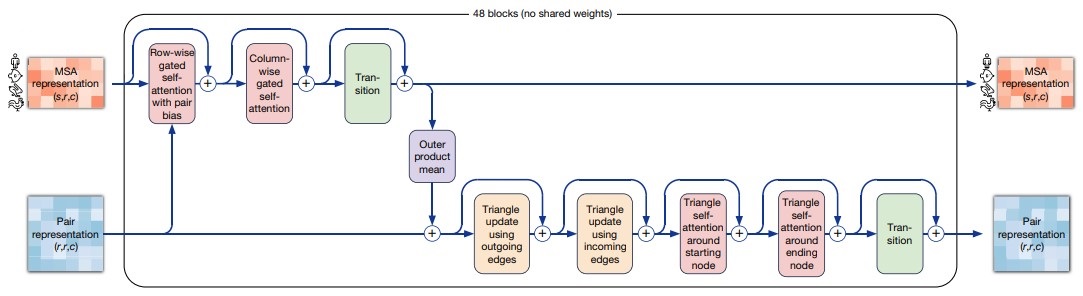
Evoformer похож на трансформер, поскольку многие операции в нем используют self-attention. Как в и трансформере, через все операции проброшены skip connections, то есть входные данные прибавляются к выходным. Операция, вокруг которой проброшен skip connection, называется residual-блоком. В некоторых residual-блоках добавляется dropout по отдельным столбцам и строкам. Общий алгоритм вычислений в evoformer stack, дублирующий рис. 12, приведен в алгоритме 6.

Большая часть операций, выполняемых в evoformer-блоке, основаны на criss-cross attention. Этот подход заключается в следующем: имея трехмерный массив, каждый -й элемент которого является вектором-эмбеддингом, мы сначала применяем операцию multi-head self-attention к каждой строке массива, затем к каждому столбцу (или наоборот).

Надо так же отметить, что evoformer-блоки, обрабатывающие MSA-кластеры, и evoformer-блоки, обрабатывающие дополнительные MSA-последовательности (см. рис. 9, extra evoformer stack), имеют некоторые отличия. Эти отличия обусловлены тем, что дополнительные таблицы MSA содержат большое количество последовательностей (в отличие от MSA-кластеров), и обрабатывающие их evoformer-блоки должны быть адаптированы для работы с большим количеством последовательностей.

Подробнее см. Supplementary Material, раздел 1.7.2

Далее мы последовательно разберем все вычислительные элементы evoformer-блока (рис. 12).

MSA row-wise and column-wise gated self-attention

Вспомним, что массив MSA representation состоит из набора последовательностей, каждая из которых состоит из набора позиций. Каждая позиция представлена вектором-эмбеддингом длиной 256. Таким образом, массив MSA representation имеет три оси, и его можно рассматривать как таблицу из векторов-эмбеддингов.

Первые два элемента evoformer-блока (row-wise self-attention, column-wise self-attention) отвечают за обновление MSA representation, при котором в векторы-эмбеддинги «обмениваются информацией» друг с другом (рис. 13, 14). Кроме того, в row-wise self-attention используется информация из pair representation.

Если в обеих схемах убрать gating, а в первой также убрать pair bias, то мы получим в точности механизм multi-head self-attention, используемый в трансформерах. Этот механизм я подробно разбирал в обзоре статьи о трансформерах (см. разделы с «Dot-product attention» до «Multi-head attention»).

В row-wise self-attention обмен информацией между векторами идет в пределах одной строки (то есть между всеми позициями в белке), в column-wise self-attention – в пределах одного столбца (то есть между одной и той же позицией во всех последовательностях).

Рис. 13. MSA row-wise gated self-attention with pair bias.

Рис. 14. MSA column-wise gated self-attention.

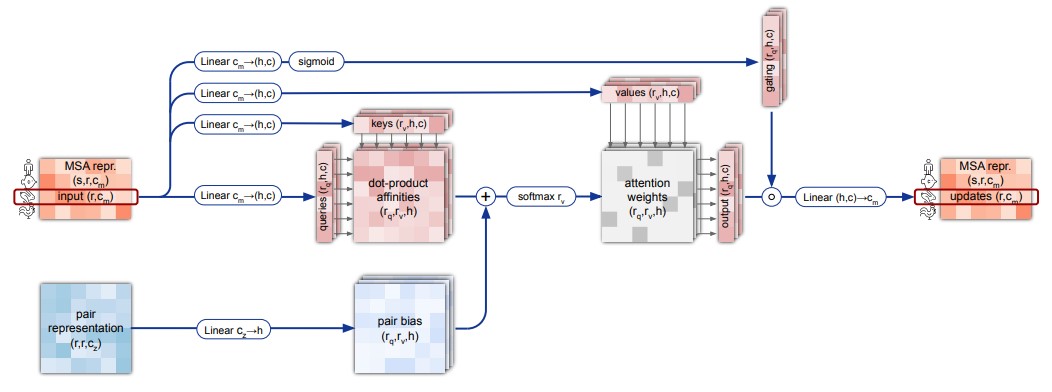
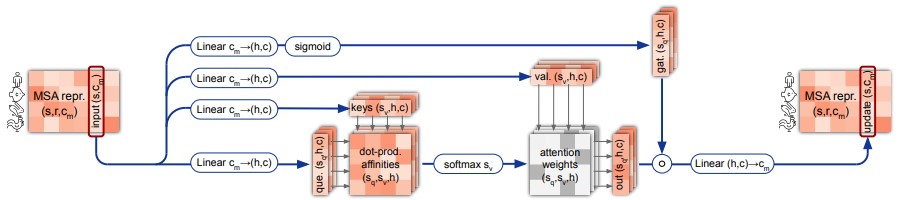
Gating заключается в том, что взвешенные средние векторов умножаются на «маску», полученную с помощью сигмоиды (рис. 13, 14). Смысл добавления gating в работе не объясняется, но это похоже на механизм multiplicative input gate и forget gate в LSTM.

Pair bias заключается в добавлении к скалярным произведениям векторов дополнительного слагаемого, рассчитанного как линейное преобразование каждого вектора в pair representation. Таким образом нейронная сеть может научиться учитывать информацию из pair representation при обновлении MSA representation. Если удалить pair bias, то pair representation никак не будет влиять на MSA representation в evoformer-блоке, что противоречит идее о том, что эти массивы должны меняться под действием друг друга.

В качестве альтернативы, можно было бы заменить row-wise и column-wise attention на общий attention между всеми возможными парами векторов в MSA representation. Однако такой способ привел бы к намного более тяжелым вычислениям и большему расходу памяти. Используя разложение attention на row-wise и column-wise, авторы ссылаются на работу CCNet: Criss-Cross Attention for Semantic Segmentation (2018).

Стоит упомянуть и еще одну деталь, не отраженную на рис. 13, 14. Каждый входной вектор в MSA representation и pair representation нормализуется L2-нормализацей до единичной длины (Layer Normalization). Алгоритм 7 дублирует рис. 13. В этом алгоритме MSA representation обозначается как $m_{si}$ , pair representation обозначается как $z_{ij}$ .

Алгоритм column-wise self-attention устроен аналогично, но без использования pair representation.

MSA transition

Следующий элемент evoformer-блока – MSA transition, в котором каждый вектор в MSA-таблице преобразуется с помощью нейронной сети с одним скрытым слоем (рис. 15).

Здесь снова все устроено так же, как в блоке трансформера. Как и в трансформере, вокруг MSA transition также проброшена связь skip connection (см. рис. 12). Также отметим, что перед первым слоем Linear выполняется операция LayerNormalization (не отражена на схеме).

Важно, что эта операция выполняется независимо и одинаково по каждому вектору в таблице MSA. Обозначим сеть со скрытым полносвязным слоем за f(x) . Тогда для любых , верно следующее: $\text{output}[s, r, :] = f(\text{LayerNorm}(\text{input}[s, r, :]))$ (используя numpy-индексацию).

Outer product mean

Блок outer product mean (рис. 16) обновляет pair representation под действием MSA representation.

Обозначим pair representation символом (), MSA representation символом (). Допустим, мы хотим обновить вектор $z_{i, j}$ . В таблице MSA representation индексам и соответствуют два столбца: $m_{:, i}$ и $m_{:, j}$ . Эти столбцы нужно использовать для обновления $z_{i, j}$ . Фактически, нам достаточно лишь придумать способ передачи информации из MSA в $z_{i, j}$ . Какая конкретно информация будет передаваться – нейронная сеть определит сама в ходе обучения.

Авторы предлагают поступать следующим образом (рис. 13). Каждый вектор-эмбеддинг столбцов $m_{:, i}$ и $m_{:, j}$ обрабатывается полносвязным слоем (для уменьшения размерности векторов-эмбеддингов с 256 до 32), и мы получаем две последовательности векторов.

Далее считаем внешнее произведение (outer product). Разберем эту операцию детально. Обе входные последовательности ( и ) имеют размер ( $N_{\text{clust}}$ , 32), где $N_{\text{clust}}$ - количество кластеров в MSA. Результат имеет размер ( $N_{\text{clust}}$ , 32, 32). Для каждого , c_1 , c_2 : $\text{output}_{s, c_1, c_2} = a_{s, c_1} * b_{s, c_2}$ .

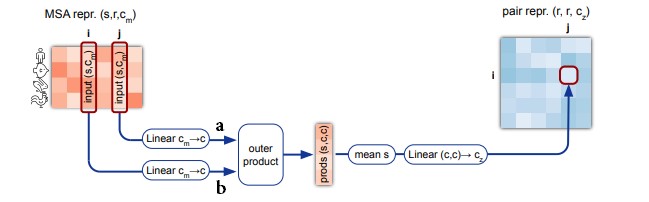
Полученный массив с тремя осями сначала усредняется по оси, соответствующей номеру кластера, затем «вытягивается» в вектор и обрабатывается полносвязным слоем. В результате получаем вектор длиной 128, который прибавляется к вектору $z_{i, j}$ .

Назовем каждый элемент вектора-эмбеддинга «признаком». Тогда суперпозиция внешнего произведения и усреднения означает, что мы считаем все попарные скалярные произведения -го признака и -го признака , то есть матрицу Грама. Это напоминает подсчет матрицы Грама между признаками в сверточных сетях при переносе стиля (см. Image Style Transfer Using Convolutional Neural Networks).

Авторы добавляют, что операция outer product mean является затратной по памяти, так как в ходе нее рассчитываются промежуточные тензоры большой размерности.

Triangular multiplicative update

Если бы массив pair representation состоял из попарных расстояний между вершинами, тогда важным было бы соблюдение неравенства треугольника: для любых i, j, k расстояние между позициями и должно быть не больше, чем сумма расстояния между позициями и и расстояния между позициями и . В противном случае построить трехмерную структуру по матрице не получится.

Не исключено, что авторы в ходе работы рассматривали и такой вариант, но решили отказаться от него в пользу более репрезентативного, когда каждая пара позиций кодируется не одним числом, а вектором-эмбеддингом. В этом случае сеть должна сама обучиться неравенству треугольника на эмбеддингах.

Элемент i, j pair representation является вектором-эмбеддингом пары позиций i, j , или, иначе говоря, эмбеддингом ориентированного ребра . Механизм triangular multiplicative update является обучаемым преобразованием, которое работает по очереди со всеми возможными тройками ребер в pair representation: для всех i, j, k обновляет эмбеддинг -го ребра с помощью эмбеддингов ребер и , а также с помощью эмбеддингов ребер и (рис. 17). Поэтому triangular multiplicative update присутствует в evoformer-блоке в двух экземплярах: «outgoing edges» и «incoming edges».

Рис. 17. Triangular multiplicative update.

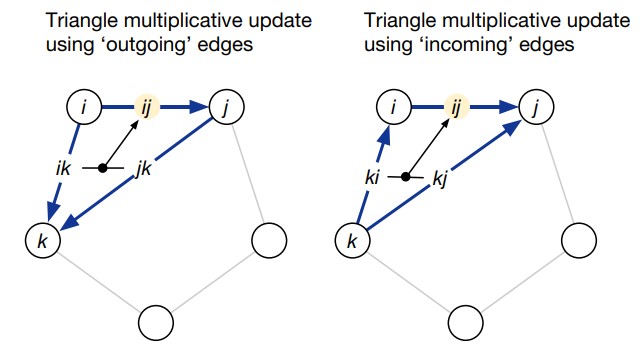
На рис. 18 и в алгоритме 11 (см. ниже) показана вычислительно эффективная матричная форма triangular multiplicative update. Операции, выполняемые в строке 4 алгоритма, линейны, поэтому знак суммы можно вынести, и таким образом Algorithm 11 можно рассмотреть как последовательность выполнений Algorithm 11 для каждого фиксированного . Благодаря этому можно упростить понимание операции triangular multiplicative update: ее можно рассмотреть как операцию, выполняемую по очереди для каждой тройки i, j, k .

Рис. 18. Triangular multiplicative update using «outgoing» edges.

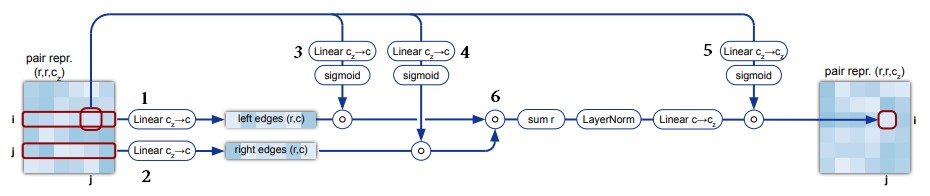
Назовем ребро целевым ребром, а ребра и смежными ребрами. Вектор-эмбеддинг целевого ребра обрабатывается полносвязным слоем с сигмоидой («5» на рис. 15), полученный вектор назовем v_1 , вектора-эмбеддинги смежных ребер обрабатываются операцией $\sigma(\text{Linear}(x)) \cdot \text{Linear} (x)$ , получая пару векторов v_2 и v_3 . Полученная пара векторов поэлементно умножается («6» на рис. 14), нормализуется L2-нормализацией до единичной длины (LayerNormalization) и снова обрабатывается полносвязным слоем, полученный вектор назовем $v_{2, 3}$ . Далее вектора $v_{2, 3}$ и v_1 поэлементно умножаются, и результат записывается в выходной массив на место эмбеддинга ребра .

Резюмируя: для всех троек чисел i, j, k к ребру добавляется слагаемое, являющееся функцией от ребер , , . Под «ребром» понимаем эмбеддинг ребра в массиве pair representation.

Аналогично операция повторяется для «incoming edges», только на этот раз мы берем функцию от ребер , , .

Подробнее см. Supplementary Material, раздел 1.6.5

Triangular self-attention

В операции «triangular self-attention around starting node» все ребра, исходящие из одной и той же вершины (строка в массиве pair representation), обмениваются между собой информацией. Для этого к строке массива pair representation применяется операция multi-head self-attention.

Аналогично, в операции «triangular self-attention around ending node» обмениваются информацией все ребра, входящие в одну и ту же вершину. Для этого к столбцу массива pair representation применяется операция multi-head self-attention.

Есть два отличия triangular self-attention (рис. 19) от стандартного multi-head self-attention. Первое отличие заключается в использовании gating («1» на рис. 19), так же как в MSA gated self-attention.

Рис. 19. Triangular self-attention around starting node.

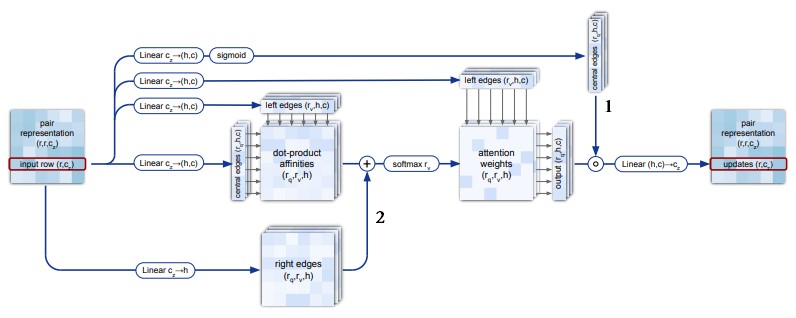
Второе отличие заключается в использовании ребер и при обмене информацией между ребрами и (рис. 20). Ниже рассмотрим этот механизм более детально.

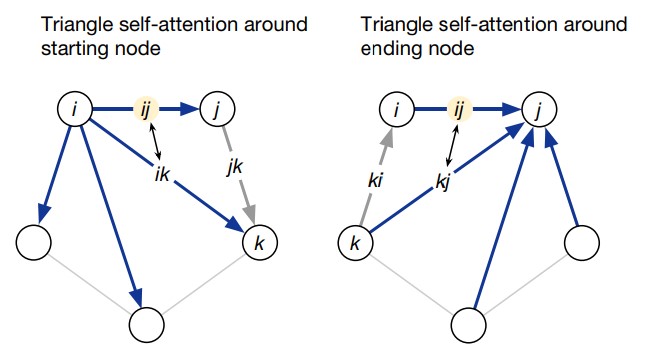
В self-attention (см. Attention Is All You Need) для обновления ребра рассчитываются скалярные произведения между query для этого ребра и keys для ребер (для всех ). Полученный набор чисел называется attention logits, или dot-product affinities (см. рис. 19). К этому набору чисел применяется softmax для получения весов. Веса затем используются для расчета взвешенного среднего.

Особенность triangular self-attention в том, что к dot-product affinities прибавляется дополнительное слагаемое («2» на рис. 19, строка 5 алгоритма 13). Например, пусть мы хотим обновить вектор-эмбеддинг ребра , используя ребро . Мы рассчитываем dot-product affinity скалярным произведением query ребра и key ребра . К полученному числу мы прибавляем еще одно число, полученное из вектора-эмбеддинга ребра с помощью линейного слоя с одним нейроном.

На рис. 19 в нижней ветке указано количество выходных нейронов , но это потому, что используется multi-head self-attention с голов. Все головы работают независимо друг от друга . В итоге операция triangular self-attention напоминает triangular multiplicative update, поскольку в ней тоже используются тройки ребер. Но отличие в том, что в triangular multiplicative update не используется механизм внимания, поэтому обмен информацией между тройкой ребер ij, ik, jk происходит без участия других ребер.

Transition in the pair stack

Эта последняя операция в evoformer-блоке выполняется аналогично операции MSA transition (рис. 15). Массив pair representation состоит из векторов-эмбеддингов каждого направленного ребра, и каждый эмбеддинг в нем обновляется с помощью полносвязной нейронной сети с одним скрытым слоем.

Structure module

Блок structure module принимает на вход данные, полученные на выходе из evoformer stack:

single representation размером $(N_{res}, 384)$ – вектора-эмбеддинги для каждой позиции
pair representation размером $(N_{res}, N_{res}, 128)$ – вектора-эмбеддинги для каждой пары позиций

Формальное представление 3D-структуры

Каждая позиция в белке – это атом $\alpha$ -углерода, крепящийся к нему аминокислотный остаток, а также пептидная связь между атомами $\alpha$ -углерода (см. рис. 6). В более простом варианте задачи достаточно предсказать координаты атомов $\beta$ -углерода («backbone»), в более сложном варианте задачи нужно предсказать координаты всех атомов белка.

В AlphaFold для каждой позиции в белке вводится локальная ортонормированная система координат (backbone frame). Ноль в этой системе соответствует координате атома $\alpha$ -углерода. Координаты всех атомов аминокислотного остатка, а также атомов пептидной связи, можно описывать как в локальной системе координат, так и в глобальной.

Переход из локальной системы координат в глобальную можно описать как поворот + смещение. Поворот описывается ортогональной матрицей, смещение – вектором. Поэтому каждой позиции в белке сопоставляется 12 чисел: матрица поворота 3x3 и вектор смещения.

Авторы вводят символ T_i для обозначения локальной системы координат -й позиции:

Переход из локальной в глобальную систему координат осуществляется умножением на матрицу R_i и прибавлением вектора t_i . Упорядоченную пару T_i («фрейм») можно рассмотреть как операцию перехода между системами координат, и записывать следующим образом:

$x_{\text{global}} = T_i \circ x_{\text{local}} = R_i x_{\text{local}} + t_i$

Введем операцию суперпозиции двух систем координат:

$T_{\text{result}} = T_1 \circ T_2$ $(R_{\text{result}}, t_{\text{result}}) = (R_1, t_1) \circ (R_2, t_2) = (R_1 R_2, R_1 t_2 + t_1)$

В AlphaFold на первом шаге координаты всех атомов $\alpha$ -углерода t_i инициализируются нулями, а все матрицы R_i – матрицами идентичности. Авторы называют этот способ «black hole initialization». Затем выполняется 8 итераций, на каждом из которых каждый фрейм T_i обновляется путем суперпозиции с другим ортонормированным фреймом, рассчитанным нейросетью. Тем самым координаты всех атомов $\alpha$ -углерода и их ориентации уточняются.

Описанный принцип авторы называют «residue gas»: фрейм каждой позиции находится в пространстве «сам по себе»: не задается явного ограничения, что -й и (i+1) -й фрейм должны находиться друг от друга на требуемом расстоянии в глобальной системе координат. Сеть сама «выучивает» это правило в ходе обучения.

С другой стороны, при таком подходе погрешность предсказания приведет к тому, что в результате мы получим невозможную структуру, где атомы $\alpha$ -углерода находятся друг от друга немного не на тех расстояниях, на каких должны быть. Поэтому для получения финального предсказания ответ нейросети уточняется итеративными алгоритмами минимизации энергии.

Помимо координат атомов $\alpha$ -углерода, нужно также определить координаты всех остальных атомов. Каждый аминокислотный остаток тоже не является «жесткой» структурой. Для расчета координат атомов в аминокислотном остатке для каждой позиции в белке вводится набор углов кручения (торсионные углы): $\omega, \phi, \psi, \chi_1, \chi_2, \chi_3, \chi_4$ . Эти углы тоже рассчитываются в structure module. Зная фреймы и углы кручения для всех позиций, можно рассчитать координаты всех атомов в белке.

Подробнее см. Supplementary Material, раздел 1.8

На рис. 21 показано, как в AlphaFold моделируется трехмерная структура белка. Фреймы задают позиции атомов $\alpha$ -углерода и ориентацию соседних атомов, а углы кручения позволяют определить позиции атомов в аминокислотных остатках.

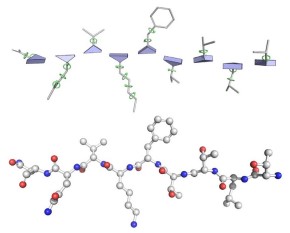
Схема вычислений в structure module

Structure module (рис. 22) состоит из 8 последовательно соединенных блоков с общими весами, то есть работает как рекуррентная сеть. Между блоками передаются два массива данных:

single representation (массив векторов-эмбеддингов), полученный из evoformer-стека
backbone frames (фреймы каждой позиции), которые изначально инициализируются методом «black hole initialization», описанным выше.

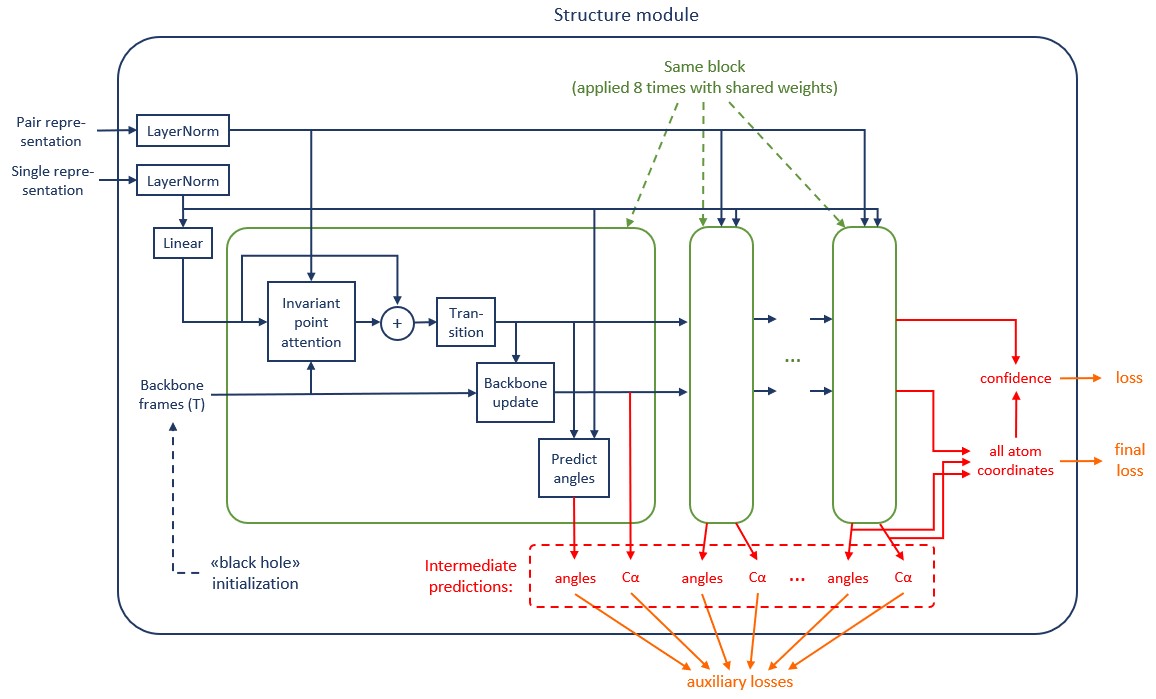
Рассмотрим операции, выполняемые внутри каждого блока.

Invariant point attention. В ходе этой операции массив single representation обновляется под действием себя самого (self-attention), а также под действием pair representation и backbone frames. Вокруг invariant point attention проброшена связь skip connection.
Transition. Каждый вектор-эмбеддинг в single representation обновляется полносвязной нейронной сетью (по аналогии с тем, как в трансформере полносвязная нейронная сеть применяется после self-attention).
Backbone update. Backbone frames обновляются под действием single representation.
Predict angles. Углы кручения рассчитываются с помощью текущего single representation и single representation, полученного из evoformer-стека.
$C\alpha$ (координаты атомов $\alpha$ -углерода) извлекаются из backbone frames, для этого берется второй компонент каждого фрейма.

В результате, выходными данными каждого блока (intermediate predictions) являются координаты атомов $\alpha$ -углерода и углы кручения для каждого аминокислотного остатка. Выходные данные последнего блока являются финальным предсказанием. По углам кручения рассчитываются координаты всех атомов в белке (all atom coordinates). Также рассчитывается уверенность в предсказаниях (confidence).

Авторы отмечают, что для стабилизации обучения AlphaFold блокируют «протекание» градиента по матрицам поворота R_i из следующего блока в предыдущий. Технически это означает следующее: в том месте, где фреймы передаются из одного блока в другой, добавляется операция StopGradient – это тождественное преобразование, градиент которого переопределяется значением 0.

We found it helpful to zero the gradients into the orientation component of the rigid bodies between iterations (Algorithm 20 line 20), so any iteration is optimized to find an optimal orientation for the structure in the current iteration, but is not concerned by having an orientation more suitable for the next iteration. Empirically, this improves the stability of training, presumably by removing the lever effects arising in a chained composition frames.

Далее более подробно рассмотрим выполняемые вычисления и функции потерь.

Invariant point attention

Схема вычислений в блоке invariant point attention показана на рис. 23. Красным цветом показана стандартная операция multi-head self-attention, применяемая к single representation. Синим цветом показано использование pair representation в расчете attention logits, а также при обновлении single representation. Использование backbone frames (зеленый цвет) подробнее разберем далее.

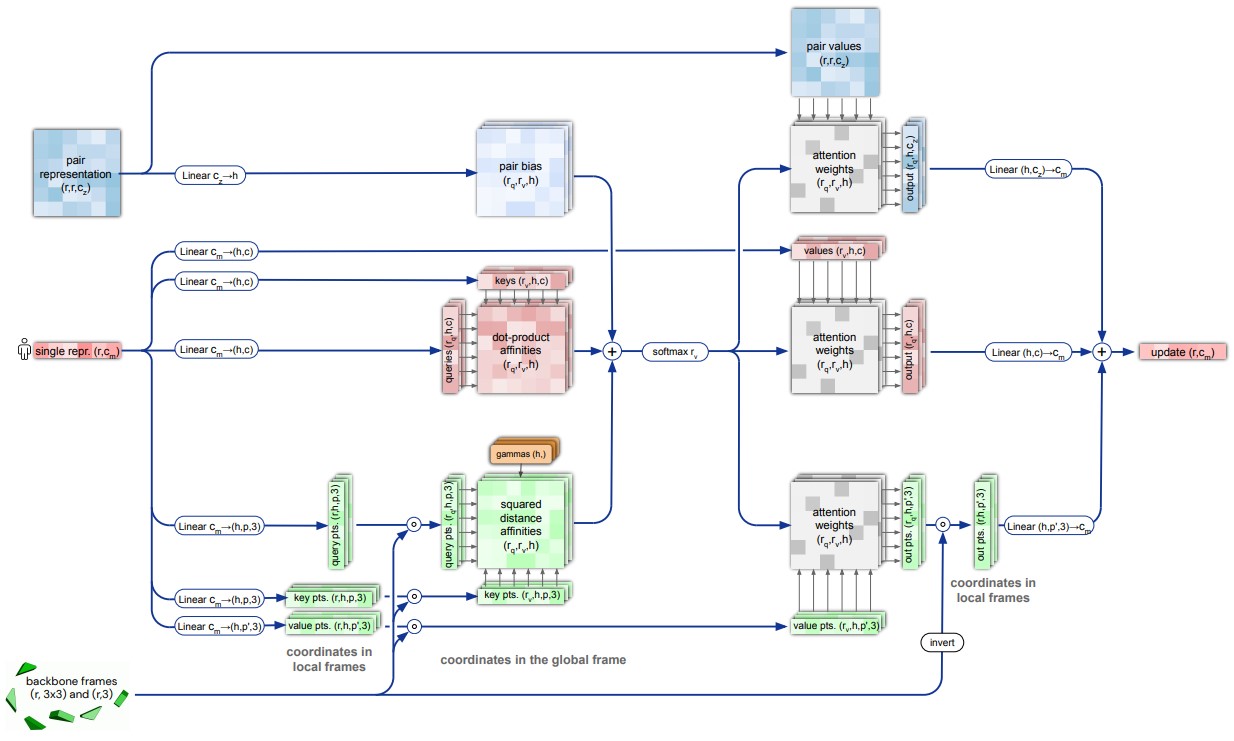
Операция invariant point attention спроектирована так, что является инвариантной к смене глобальной системы координат в backbone frames. Это важное свойство: обновление single representation должно происходить с учетом структуры белка (точнее, ее приближения на текущей итерации), которая не зависит от выбранной системы координат.

В алгоритме 22 показано, как конкретно используются backbone frames. Для упрощения можно принять $N_{\text{head}} = 1$ и избавиться от индексов в алгоритме. Зафиксируем пару позиций и . Этим позициям соответствуют вектора-эмбеддинги s_i, s_j и фреймы T_i, T_j .

Линейными преобразованиями рассчитываются 4 вектора в трехмерном пространстве: ${q_i^1, q_i^2, q_i^3, q_i^4}$ (query points). Эти вектора переводятся из локальной системы координат в глобальную систему координат.
Линейными преобразованиями рассчитываются 4 вектора в трехмерном пространстве: ${k_j^1, k_j^2, k_j^3, k_j^4}$ (key points). Эти вектора переводятся из локальной системы координат в глобальную систему координат.

В результате получаем 4 вектора-ключа и 4 вектора значения в глобальной системе координат. Между парами этих векторов рассчитываются квадраты расстояний, и складываются. Результат умножается на константу и добавляется к dot-product affinities (строка 7 в алгоритме 22). Данная операция является инвариантной к смене глобальной системы координат, что ясно из геометрических соображений.

Смысл данной операции, по-видимому, следующий: обучившись использовать подходящие вектора queries и keys, в зависимости от типа аминокислотного остатка, нейронная сеть может научиться моделировать взаимодействия между разными аминокислотными остатками. Полученные вектора в локальной системе координат могут означать некие ключевые точки для данного остатка. Расстояния между парами точек могут кодировать взаимодействие двух аминокислотных остатков.

Теперь рассмотрим, как backbone frames используются в строке 11 алгоритма 22, где на основании attention weights обновляется вектор single representation.

Обновляя -ю позицию, мы имеем attention weights для каждой -й позиции $a_{ij}$ . Для каждой -й позиции рассчитывается 8 векторов в локальной системе координат T_j : ${v_j^1, v_j^2, \dots, v_j^8}$ (point values). Эти вектора переводятся в глобальную систему координат, где считается из взвешенное среднее с помощью весов $a_{ij}$ . Полученный вектор переводится в локальную систему координат T_i , и результат после линейного преобразования добавляется к эмбеддингу -го вектора. Такая операция напоминает расчет «взвешенного центра масс» и тоже является инвариантной к преобразованиям глобальной системы координат.

Доказательство инвариантности см. в Supplementary Material, раздел 1.8.2

Другие операции в structure module

Операция transition (см. рис. 22) является нейронной сетью с 2 скрытыми слоями, вокруг которой проброшена связь skip connection. Также в начале и конце добавляются LayerNorm и Dropout.

Операция backbone update заключается в коррекции каждого фрейма T_i с помощью матрицы поворота и вектора смещения. Любой поворот в трехмерном пространстве можно описать кватернионом, первый элемент которого равен 1. Кватернион рассчитывается линейным преобразованием эмбеддинга -й позиции, и затем преобразуется в матрицу поворота (алгоритм 23).

Подробнее см. Supplementary Material, раздел 1.8.3

Операция predict angles позволяет получить углы кручения для -й позиции с помощью эмбеддинга этой позиции. Для этого используется нейронная сеть с несколькими слоями и skip connections, которая также использует изначальный эмбеддинг -й позиции, полученный из evoformer-блока. Углы предсказываются как точки на единичной окружности: рассчитывается вектор из двух чисел и нормализуется до единичной длины.

Подробнее см. Supplementary Material, Algorithm 20, строки 11-14

Влияние архитектуры structure module на метрику качества

Несмотря на сложность операций, выполняемых в structure module, их положительное влияние оказывается лишь незначительным. Авторы демонстрируют, что радикальное упрощение structure module, включая избавление от рекуррентности и invariant point attention, а также отказ от использования pair representation в structure module ведет лишь к незначительному ухудшению метрики качества.

См. также Supplementary Material, раздел 1.13, Figure 10, “No IPA”

Функции потерь в AlphaFold

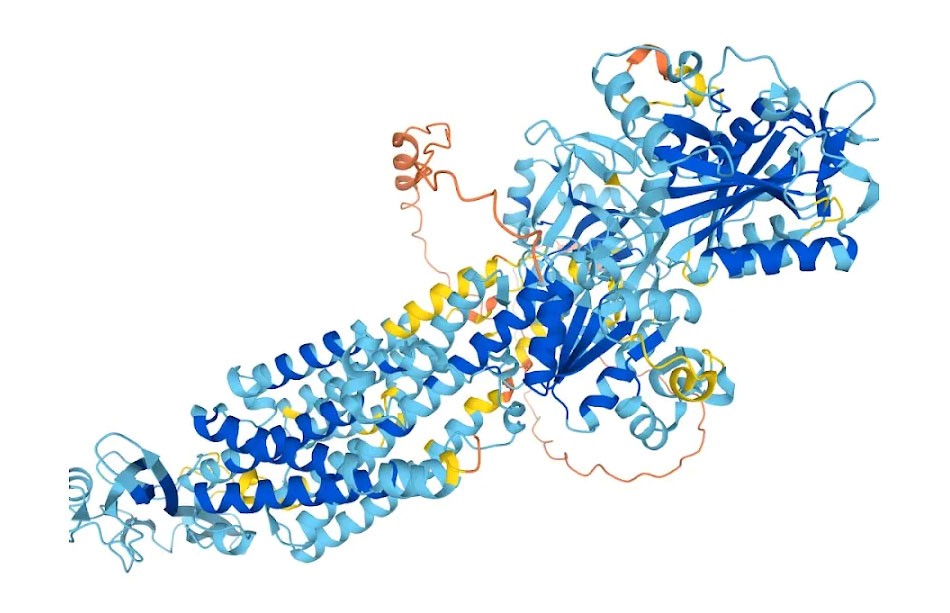
Как это часто бывает в сложных архитектурах, в AlphaFold минимизируется сумма нескольких разных функций потерь. Обучение AlphaFold проходит в два этапа. Второй этап, называемый fine-tuning, отличается большим размером кропа и таблицы MSA, меньшим learning rate, а также в нем добавлены еще две функции потерь (рис. 24).

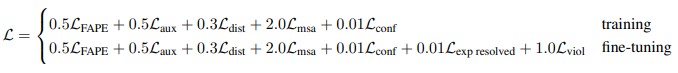
$\mathcal{L}_{\text{FAPE}}$ – основная функция потерь в AlphaFold, сравнивающая предсказанную 3D-структуру белка с эталонной. Она рассчитывается на последней итерации в structure module (final loss на рис. 22). Далее эта функция потерь будет рассмотрена подробнее.

$\mathcal{L}_{\text{aux}}$ – дополнительная функция потерь (auxiliary loss), рассчитываемая после каждой итерации в structure module. Эта функция является суммой двух слагаемых. Первое слагаемое – упрощенный вариант FAPE, в котором рассчитывается ошибка предсказания только для атомов $\alpha$ -углерода (а не для всех атомов белка). Второе слагаемое – torsion angle loss, который сравнивает предсказанные углы кручения с эталонными (подробнее см. далее).

Torsion angle loss рассматривается как дополнительная функцией потерь, поскольку минимизация основной функции потерь FAPE должна приводить также и к минимизации ошибки предсказания углов. Но добавление дополнительных функций потерь в тех местах, где мы знаем, как должен выглядеть ответ, может улучшить стабильность и качество обучения.

The purpose of the FAPE, aux, distogram, and MSA losses is to attach an individual loss to each major subcomponent of the model (including both the pair and MSA final embeddings) as a guide during the training of the “purpose” of each unit.

Подробнее см. Supplementary Material, раздел 1.9

Чтобы уменьшить относительную важность коротких последовательностей, суммарная функция потерь умножается на квадратный корень из длины белка (которая ограничена сверху размером кропа). Такое действие побуждает модель повышать точность предсказания на длинных белках, особенно учитывая тот факт, что их меньше, чем коротких (см. рис. 5).

Далее рассмотрим подробнее FAPE и torsion angle loss, затем остальные функции потерь.

Frame aligned point error (FAPE)

FAPE – основная функция потерь AlphaFold, которая сравнивает предсказанную 3D-структуру с эталонной. Для понимания функции FAPE понадобится снова вспомнить понятие «фрейм» (backbone frame) – локальная ортонормированная система координат, связанная с -м атомом $\alpha$ -углерода. Подробнее о понятии фрейма см. раздел «Формальное представление 3D-структуры».

Функция FAPE может быть реализована в двух вариантах: либо она принимает только координаты атомов $\alpha$ -углерода, либо координаты всех атомов белка. Рассмотрим только первый случай как более простой. В этом случае в алгоритме 28 x_i является началом координат во фрейме T_i , и аналогично $x_i^{\text{true}}$ является началом координат во фрейме $T_i^{\text{true}}$ . Тогда второй и четвертый аргументы излишни, и можно считать, что функция $\text{computeFAPE}$ принимает только два аргумента:

– фрейм для -й позиции в предсказанной структуре
$T_i^{\text{true}}$ – фрейм для -й позиции в эталонной структуре

Зафиксировав пару позиций и , можно рассчитать координату -го атома во фрейме, связанном с -м атомом. Выполним такое действие в предсказанных и в эталонных координатах, мы получим векторы $x_{ij}$ и $x_{ij}^{\text{true}}$ , которые не будут зависеть от поворота и смещения глобальной системы координат. Далее считаем расстояние между $x_{ij}$ и $x_{ij}^{\text{true}}$ , которое ограничиваем сверху значением 10 ангстрем. Полученные значения усредняем по всем i, j .

Функция FAPE является инвариантной к повороту и смещению глобальной системы координат как в предсказанном, так и в эталонном наборе координат, но не инвариантна к отражению системы координат, что важно при предсказании структуры белков.

В AlphaFold 2 функция потерь FAPE для атомов $\alpha$ -углерода рассчитывается после каждой итерации в structure module (auxiliary losses на рис. 22). Плюс к этому, на последней итерации рассчитывается FAPE для всех атомов в белке (final loss на рис. 22).

Еще одна особенность заключается в том, что некоторые аминокислотные остатки симметричны. Например, симметричным является остаток тирозина. Если в предсказанной структуре остаток будет повернут на 180 градусов относительно эталонной структуры, то ответ будет тоже правильным, хотя координаты отдельных атомов в FAPE не совпадут. Чтобы решить эту проблему, авторы вводят дополнительную операцию «rename symmetric ground truth atoms», которая делает предсказание по возможности более похожим на ответ, «разворачивая» симметричные остатки на 180 градусов.

Подробнее см. Supplementary Material, разделы 1.9.2-1.9.5, 1.8.5

Torsion angle loss

Углы кручения в AlphaFold предсказываются как точки на единичной окружности. Как было описано выше, для предсказания углов в AlphaFold сначала рассчитывается произвольный вектор из двух чисел, а затем этот вектор нормализуется до единичной длины. На каждой итерации в structure module рассчитываются углы (см. рис. 22), и добавляются две дополнительные функции потерь:

Первая функция потерь «штрафует» слишком большие или слишком маленькие вектора до нормализации, чтобы предотвратить стремление этих векторов к нулю или бесконечности.

Вторая функция потерь сравнивает предсказанные углы с эталонными, рассчитывая L2-норму разности между ними. Однако некоторые аминокислотные остатки симметричны, и угол 180° эквивалентен углу 0°. Это учитывается путем предоставления «альтернативных» эталонных углов.

Подробнее см. Supplementary Material, раздел 1.9.1

MSA loss

$\mathcal{L}_{\text{msa}}$ – точность предсказания ячеек таблицы MSA, закрытых маской. На этапе подготовки данных маскировалось 15% ячеек таблицы MSA (см. раздел «Кластеризация и маскирование таблицы MSA»). Задача их предсказания аналогична задаче «masked language model» в языковой модели BERT. Для предсказания используется массив MSA representations, полученный на выходе из evoformer stack. По каждому вектору в MSA representations линейным слоем осуществляется классификация в один из типов аминокислотных остатков, и в качестве функции потерь используется кроссэнтропия.

Подробнее см. Supplementary Material, раздел 1.9.9

Distogram loss

$\mathcal{L}_{\text{dist}}$ – loss предсказания дистограммы. Дистограммой называется матрица попарных расстояний между атомами $\beta$ -углерода. Для предсказания дистограммы авторы добавляют в модель дополнительный выходной слой (distogram head), который линейно отображает каждый вектор из pair representation в распределение вероятностей для элемента дистограммы. Пространство R^+ делится на 64 интервала, и задача рассматривается как классификация с 64 классами, каждый класс соответствует одному из интервалов – то есть здесь используется тот же подход, что и при создании дистограмм шаблонов (см. раздел «Данные о шаблонах»).

Подробнее см. Supplementary Material, раздел 1.9.8

Авторы проводят дополнительные эксперименты, удаляя или упрощая различные блоки в AlphaFold и изучая, как это скажется на качестве. Выясняется, что во-первых отказ от использования distogram loss ведет лишь к незначительному падению качества предсказаний.

Во-вторых, блокировка протекания градиента из structure module в evoformer stack (то есть теперь evoformer stack обучается только под действием distogram loss и MSA loss) ведет к существенному падению качества. Это говорит о том, что минимизировать лишь distogram loss недостаточно для качественного обучения.

Вспомним, что радикальное упрощение structure module вело лишь к небольшому падению точности. Это говорит о том, что для высокой точности предсказаний важна не столько сложность structure module, сколько его наличие, то есть предсказание 3D-структуры, а не дистограммы. Возможно это связано с тем, что дистограмме соответствует две зеркальные структуры, и лишь одна из них правильная.

См. также Supplementary Material, раздел 1.13, Figure 10

Confidence loss

$\mathcal{L}_{\text{conf}}$ – loss для оценки уверенности в предсказаниях. Уверенность оценивается следующим образом: между предсказанной и эталонной структурой для каждой позиции рассчитывается метрика локального сходства LDDT (специфичная для задачи предсказания структуры белка), а затем модель учится предсказывать рассчитанное значение LDDT для каждой позиции. На рис. 25 показана предсказанная структура белка (другие структуры можно посмотреть здесь).

Рис. 25. Предсказанная структура одного из белков. Области с высокой уверенностью отмечены синим, области с низкой уверенностью отмечены оранжевым.

Violation losses

$\mathcal{L}_{\text{viol}}$ – сумма функций потерь, которые «штрафуют» предсказанные структуры, невозможные физически. Такое иногда происходит из-за применения концепции «residue gas» (см. раздел «Формальное представление 3D-структуры»). Violation losses рассчитываются только на втором этапе обучения (fine-tuning), тем самым модель подталкивается к тому, чтобы предсказывать физически корректные структуры даже в тех случаях, когда она не уверена в предсказаниях.

“Violation” losses encourage the model to produce a physically plausible structure with correct bond geometry and avoidance of clashes, even in cases where the model is highly unsure of the structure. … Using the violation losses early in training causes a small drop in final accuracy since the model overly optimizes for the avoidance of clashes, so we only use this during fine-tuning.

Процесс обучения AlphaFold

Обучение AlphaFold выполняется в два этапа, как было описано в разделе «Функции потерь в AlphaFold». Также при обучении используется механизм recycling, как было описано в разделе «Применение recycling в AlphaFold».

Исходный код можно найти в этом репозитории. Для подготовки данных использовался пайплайн TensorFlow версии 1.x, для прямого и обратного прохода использовалась библиотека JAX.

Оптимизатор и learning rate

Для обучения используется оптимизатор Adam c параметрами learning rate $10^{−3}$ , $\beta_1$ = 0.9, $\beta_2$ = 0.999, $\epsilon$ = $10^{−6}$ . Используется размер батча 128: по одному элементу батча на каждое ядро TPU. Learning rate линейно растет («warm-up») в течение первых 128 тысяч батчей и умножается на 0.95 после 6.4 миллионов батчей. На втором этапе обучения learning rate уменьшается в 2 раза.

Для стабилизации обучения используется gradient clipping по глобальной L2-норме 0.1, независимо по каждому примеру в батче. Можно предположить, что за счет очень маленького значения L2-нормы gradient clipping оказывает принципиальное влияние на обучение.

Инициализация весов

Линейные слои с функцией активации ReLU инициализируются методом He normal.
Линейные слои, используемые для проекции векторов в keys, queries, values инициализируются методом Glorot uniform.
Другие линейные слои инициализируются методом LeCun normal.
В каждом residual-блоке последний слой инциализируется нулями.
Выходные слои AlphaFold также инициализируются нулями.
Линейные слои с сигмоидой, используемые в gating (см. раздел «Evoformer») инициализируются нулями, при этом их bias’ы инициализируются единицами. Тем самым обеспечивается «открытое состояние» всех гейтов в начале обучения.

Dropout

В evoformer-блоках (см. алгоритм 6) используются модификации dropout: row-wise и column-wise. Например, $\text{DropoutRowwise}$ , действующий на массив MSA representation размером ( $N_{clust}$ , $N_{res}$ , $N_{channel}$ ) (без учета размера батча), генерирует случайную бинарную маску размером (1, $N_{res}$ , $N_{channel}$ ), и перемножает ее с массивом MSA representation.

Уменьшение потребления памяти

При обучении требуется сохранять выходные данные промежуточных слоев, чтобы затем выполнить обратный проход и рассчитать градиенты. Однако в сети AlphaFold есть места, где промежуточные данные имеют очень большой размер. Например, в triangular self-attention размер промежуточного массива $a_{ijk}^h$ (см. алгоритм 13) пропорционален третьей степени количества позиций ( $N_{res}$ ). Хранение этого массива в формате bfloat16 (2 байта) для всех 48 слоев evoformer-стека потребовало бы 20 гигабайт памяти для одного обучающего примера.

Для сокращения объема требуемой памяти авторы используют технику gradient checkpointing, иначе называемую rematerialization. При этом сохраняются только массивы, передаваемые между evoformer-блоками. Когда обратное распространение ошибки доходит до -го блока, заново делается прямой проход по этому блоку и рассчитываются градиенты. Таким образом, потребление памяти сокращается в десятки раз, а время одного шага обучение увеличивается лишь на 33%.

Еще одна техника сокращения потребления памяти применяется при инференсе. Если белок, для которого требуется рассчитать структуру, имеет очень большую длину (например, один из белков имеет длину 2180), то в каждом evoformer-блоке массив $a_{ijk}^h$ будет иметь размер 154 гигабайта. Для уменьшения объема требуемой памяти этот массив рассчитывается не целиком, а по частям, благодаря аддитивности операции triangular self-attention.

We identify a ‘batch-like’ dimension where the computation is independent along that dimension. We then execute the layer one ‘chunk’ at a time, meaning that only the intermediate activations for that chunk need to be stored in memory at a given time.

Авторы ссылаются на статью Reformer: The Efficient Transformer, где используется такой же подход.

Подробнее см. Supplementary Material, раздел 1.11.8

Self-distillation

Обучив одну модель на доступных исходных данных (MSA-последовательностях и 3D-структурах известных белков), авторы затем обучают следующую модель на датасете, состоящем на 75% из 3D-структур, предсказанных предыдущей моделью. Такой способ обучения, называемый noisy-student self-distillation, ранее применялся в сверточных сетях (Self-training with noisy student improves imagenet classification, 2019), и также здесь прослеживается связь с более ранней работой Do Deep Nets Really Need to be Deep? (2013), где использовался аналогичный подход.

Подробнее см. Supplementary Material, раздел 1.3

Дополнительные разделы статьи

Ablation studies

Авторы пробуют удалять из AlphaFold различные компоненты и исследуют как это скажется на точности предсказаний. О результатах таких экспериментов уже упоминалось в разных частях этого обзора.

Network probing

В течение трех recycling iterations информация трижды проходит через каждый из 48 evoformer-блоков. Авторы присоединяют по одному дополнительному structure module к выходу каждого evoformer-блока на каждой итерации и обучают эти модули, блокируя протекание градиента из них в evoformer-блоки. Тем самым, дополнительные structure modules учатся предсказывать 3D-структуру по промежуточным выходным данным сети AlphaFold, при этом эти дополнительные модули не оказывают влияния на обучения основной части сети.

Таким образом, при инференсе мы получаем не только финальное предсказание 3D-структуры, но и 192 дополнительных предсказания – по одному для каждого evoformer-блока в каждой итерации. На рис. 26 показана точность предсказаний по метрике global distance test (GDT) для трех белков. Как видим, для простых белков AlphaFold почти сразу находит верную структуру, а для более сложных белков требуется несколько end-to-end запусков сети.

Рис. 26. Точность промежуточных предсказаний AlphaFold.

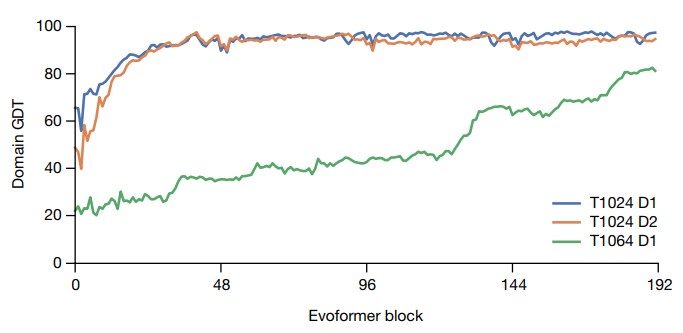
Приведенные ниже видео показывают эволюцию предсказанных структур в ходе recycling iterations (номер кадра соответствует позиции по горизонтальной оси на рис. 26).

Резюме

В этом разделе еще раз суммирована основная информация из данного обзора.

Для предсказания структуры белка мы в первую очередь ищем в базе данных другие похожие белки. Из этих белков составляется таблица MSA (multiple sequence alignment). Белки в таблице MSA как правило являются эволюционными родственниками. Мутации обычно затрагивают участки белка, не критично важные для сохранения его структуры, либо происходят парные мутации – в противном случае белок теряет свою функцию, и организм отсеивается естественным отбором. Благодаря этому по таблице MSA можно строить гипотезы о структуре белка. Если же в таблице MSA есть белки с уже известной 3D-структурой, то можно использовать и эту информацию («шаблоны»).

Входными данными для AlphaFold являются:

Аминокислотная последовательность исследуемого белка
MSA-таблица исследуемого белка
Набор шаблонов (опционально)

Архитектура AlphaFold состоит из трех последовательно соединенных блоков.

В первом блоке (feature embeddings) входные данные переводятся в эмбеддинги. Выходными данными блока являются:

MSA representation – абстрактное представление MSA-таблицы. Массив с тремя осями (без учета размера батча): номер последовательности, номер позиции в белке, номер элемента эмбеддинга.
Pair representation – абстрактное представление взаимодействий между каждой парой позиций в белке. Массив с тремя осями: номер первой позиции, номер второй позиции, номер элемента эмбеддинга.

Pair representation можно считать обобщением массива попарных расстояний (дистограммы), и интерпретировать как эмбеддинги ребер в полносвязном ориентированном графе между всеми позициями в белке.

Второй блок (evoformer stack) состоит из 48 последовательно соединенных evoformer-блоков. Каждый evoformer-блок состоит из последовательности операций, и вокруг каждой операции проброшен skip connection. Большая часть операций, выполняемых в evoformer-блоке – это multi-head self-attention, работающий по строкам или по столбцам массивов MSA representation и pair representation. Дополнительно выполняются следующие операции:

Pair bias и outer product mean – операции, позволяющие передавать информацию от pair representation в MSA representation и обратно.
Triangular multiplicative update и triangular self-attention – операции, в которых для обновления ребра используется информация из ребер и , а также из ребер и . Если pair representation можно считать обобщением дистограммы, то эти операции можно рассматривать как обучаемое обобщение неравенства треугольника.
Attention gating – модификация механизма внимания с «гейтами», по аналогии с input gate и forget gate в LSTM.

Третий блок, structure module, создает трехмерную структуру, используя в качестве входных данных:

Single representation – первую строку MSA representation, полученную на выходе из evoformer stack. Ее можно рассматривать как вектор-эмбеддинг для каждой позиции в белке.
Pair representation, полученный на выходе из evoformer stack. Вектор-эмбеддинг для каждой пары позиций в белке.

Трехмерная структура белка представляется как массив backbone frames, называемый также «residue gas» - набор локальных ортонормированных систем координат, связанных с каждой позицией в белке. На residue gas не накладывается явного ограничения, что позиции должны быть объединены в цепочку – это правило сеть выучивает самостоятельно. Все координаты инициализируются нулями.

Блок structure module устроен достаточно сложно. В нем используется invariant point attention (IPA), в котором single representation обновляется под действием backbone frames, но инвариантно к смене глобальной системы координат в backbone frames. Функция потерь FAPE также инвариантна к смене глобальной системе координат (повороту, смещению) как в предсказанной, так и в эталонной структуре.

Помимо основной функции потерь минимизируется набор дополнительных функций потерь (auxiliary losses), например loss предсказания гистограммы по pair representation и loss предсказания пропусков в MSA representation (как в BERT). Для улучшения качества предсказания модель запускается несколько раз (recycling), каждый раз получая на вход предыдущее предсказание (вместе с шаблонами 3D-структуры).

Авторы отмечают, что радикальное упрощение structure module (включая удаление IPA) лишь немного ухудшает качество предсказания, тогда как минимизация только loss предсказания дистограммы существенно ухудшает качество. Из этого можно сделать вывод, что важна не столько сложность блока structure module, сколько его наличие и распространение градиента из этого модуля в evoformer stack.

Данный обзор первоначально размещен на моем сайте www.generalized.ru, там вы можете найти обзоры и на другие статьи.

Комментарии (2)

bbs12
30.11.2021 20:05
#23770045
Это будет в учебниках будущего, раздел "Начало эпохи ИИ".
1. Balling
  05.12.2021 14:30
  #23787791
  Прошлого. Уже используется во всю. Из последнего: www.biorxiv.org/content/10.1101/2021.10.26.465776v3
  
  И больше, www.science.org/doi/10.1126/science.abm4805