Интерпретация моделей и диагностика сдвига данных: LIME, SHAP и Shapley Flow / forpes.ru

Главная
Интерпретация моделей и диагностика сдвига данных: LIME, SHAP и Shapley Flow

Интерпретация моделей и диагностика сдвига данных: LIME, SHAP и Shapley Flow +24

13.01.2022 15:34

boygenius 0 1300 Источник

В этом обзоре мы рассмотрим, как методы LIME и SHAP позволяют объяснять предсказания моделей машинного обучения, выявлять проблемы сдвига и утечки данных, осуществлять мониторинг работы модели в production и искать группы примеров, предсказания на которых объясняются схожим образом.

Также поговорим о проблемах метода SHAP и его дальнейшем развитии в виде метода Shapley Flow, объединяющего интерпретацию модели и многообразия данных.

Содержание

Интерпретация моделей машинного обучения
    Распределение данных
    Сдвиг данных
    Утечка данных
    Локальная интерпретация моделей
LIME: Local Interpretable Model-agnostic Explanations
    Локальное упрощенное представление
    Объясняющая модель
    Примеры и обсуждение
    LIME-SP: объединение локальных интерпретаций в глобальную
SHAP: Shapley Additive Explanation Values
    Shapley values в теории игр
    Shapley regression values
    SHAP values
    Проблемы и ограничения SHAP values
    Independent SHAP
    Kernel SHAP
    Tree SHAP
SHAP на практике
    Waterfall plot
    Summary plot
    Dependence plot
    Диагностика сдвига данных с помощью SHAP loss values
    Supervised-кластеризация данных с помощью SHAP
Проблемы SHAP values
    SHAP values в условиях взаимной зависимости признаков
    Соблюдение границ многообразия данных
Shapley Flow
    Использование метода Shapley Flow
    Принцип работы метода Shapley Flow
Заключение
Список источников

Интерпретация моделей машинного обучения

Модели машинного обучения (такие как нейронные сети, машины опорных векторов, ансамбли решающих деревьев) являются "прозрачными" в том смысле, что все происходящие внутри них вычисления известны. Но тем не менее часто говорят, что модели машинного обучения плохо интерпретируемы. Здесь имеется в виду то, что процесс принятия решения не удается представить в понятной человеку форме, то есть:

Понять, какие признаки или свойства входных данных влияют на ответ
Разложить алгоритм принятия решения на понятные составные части
Объяснить смысл промежуточных результатов, если они есть
Описать в текстовом виде алгоритм принятия решения (возможно, с привлечением схем или графиков)

Достичь полной интерпретируемости в машинном обучении, как правило, не удается, но даже частичная интерпретация может существенно помочь. Обзор способов интерпретации моделей машинного обучения можно найти, например, в Linardatos et al., 2020 и Li et al., 2021. Чем же может помочь интерпретация модели?

Во-первых, интерпретировав алгоритм, мы можем открыть для себя что-то новое о свойствах исследуемых данных (например, какие признаки в табличных данных в наибольшей степени влияют на ответ).

The need to explain predictions from tree models is widespread. It is particularly important in medical applications, where the patterns uncovered by a model are often even more important than the model’s prediction performance. (Lundberg et al., 2019)

Во-вторых, интерпретация модели помогает оценить ее качество. Если мы узнаем, на что именно обращает модель, какими правилами руководствуется при предсказании, то сможем оценить правдоподобность этих правил.

Humans usually have prior knowledge about the application domain, which they can use to accept (trust) or reject a prediction if they understand the reasoning behind it. (Ribeiro et al., 2016)

Казалось бы, разве недостаточно знать метрику качества модели на тестовой выборке? Часто может оказаться, что после развертывания модель работает в среднем хуже, чем на тестовой выборке из-за ряда проблем, таких как сдвиг и утечка данных.

Распределение данных

На протяжении всего обзора будет использоваться понятие распределения данных, поэтому сначала повторим значение этого понятия.

Если модель использует входных признаков, и -й признак принимает значения из множества X_i , то все пространство признаков равно $X = X_1 \times X_2 \times \dots \times X_N$ . Однако на практике далеко не все сочетания этих признаков возможны, то есть область реальных данных представляет собой лишь малую часть пространства .

Как правило, в машинном обучении используется статистический подход (statistical learning framework), при котором имеющийся датасет $D = \{x_i, y_i\}_{i=1}^\ell$ рассматривается как выборка из совместного распределения данных P(x, y) = P(x) P(y|x) , иногда называемого также генеральной совокупностью. Конечно, представление датасета как взятого из распределения P(x, y) довольно условно, потому что обычно мы имеем лишь конечную выборку данных, но не имеем строгого определения для P(x, y) . Но в целом мы считаем, что P(x) наиболее велико для "типичных" примеров , и равно нулю для невозможных примеров. P(x, y) также задает вероятность для любого пожмножества примеров.

Например, пусть мы имеем датасет из объявлений о продаже автомобилей. Для нашего датасета верно, например, следующее:

Количество авто "Lada Granta" превосходит количество авто "Москвич-412"
Количество авто "Победа" с двигателем мощностью 500 л. с. равно нулю

Тогда мы можем считать датасет выборкой из распределения, в котором для P(x) верно следующее:

$P(x|\text{марка}(x) = \text{"Lada Granta"}) > P(x|\text{марка}(x) = \text{"Москвич-412"})$
$P(x|\text{марка}(x) = \text{"Победа"}\ \&\ \text{мощность}(x) \approx \text{"500 л. с."}) \approx 0$

Таким образом, описывает соотношение разных типов примеров, и датасет рассматривается как выборка из . На таком подходе основана большая часть теоретических исследований, посвященных машинному обучению, в которых доказывается эффективность тех или иных методов.

Модели машинного обучения делятся в основном на дискриминативные и генеративные, при этом генеративные моделируют P(x) или P(x, y) , а дискриминативные - только P(y|x) , при этом в регрессии, как правило, упрощая его до мат. ожидания $E_{x \sim P(x)}[y|x]$ . Если ваша модель предсказывает целевой признак по исходным - то это дискриминативная модель. Но такие модели не выучивают никакой информации о распределении P(x) , то есть о том, насколько правдоподобно сочетание входных признаков и лежит ли оно в области реальных данных, то есть само многообразие данных не моделируется.

Сдвиг данных

Сдвиг данных (data shift) означает, что данные, на которых модель будет применяться, среднестатистически отличаются от тех, на которых модель обучалась и тестировалась, то есть распределение входных данных отличается при тестировании и применении: $P_{test}(X, Y) \neq P_{usage}(X, Y)$ . Поскольку P(X, Y) = P(Y|X)P(X) , то двумя вариантами сдвига данных являются:

Сдвиг в распределении исходных данных
Сдвиг в условном распределении целевой переменной

Проблема 1. Большинство метрик качества (accuracy, MSE, logloss, F1 и другие) зависят от распределения исходных данных P(X) , то есть, упрощенно говоря, от соотношения разных типов примеров в датасете. Например, пусть модель тестировалась на датасете, в котором 80% изображений были высокого качества (HQ), а применяться будет в условиях, когда, наоборот, 80% изображений будут низкого качества (LQ). Пусть мы сравниваем две модели: на HQ-изображениях точность первой модели лучше, чем второй, а на LQ-изображениях, наоборот, точность второй модели лучше, чем первой. Если при тестировании большая часть изображений были HQ, то мы сделаем вывод, что первая модель лучше, тогда как на самом деле лучше была бы вторая.

Проблема 2. В обучающих и тестовых данных могут присутствовать такие корреляции, которые не обобщаются на другие выборки. Например, мы классифицируем животных по изображению, но большинство изображений рыб, которые у нас имеются, содержат также пальцы рыбака (эти изображения мы используем как при обучении, так и при тестировании). Модель может научиться классифицировать как рыбу изображение, содержащее пальцы, что в целом неверно и может не работать на других выборках (Brendel and Bethge, 2019).

Проблема 3. Обучающие данные часто недостаточно разнообразны, то есть не покрывают все те типы примеров, на которых желательна корректная работа модели (либо покрывают их в неправильном соотношении). Поэтому при применении модели могут встречаться примеры таких типов, которые никогда не встречались при обучении или встречались редко, то есть лежали вне распределений $P_{train}$ и $P_{test}$ (out-of-distribution, OOD). Иными словами, $\{x | P_{train}(x) > 0\} \subsetneq \{x | P_{usage}(x) > 0\} \subsetneq X$ (рис. 1), и модель, обучающаяся на $P_{train}$ , может не научиться корректно работать на $P_{usage}$ . Таким образом, примеры некоторых типов не встречались при обучении, но на них желательна корректная работа модели, как минимум для защиты от атак, "обманывающих" модель (рис. 1) (cм. Brown et al., 2017; Akhtar and Mian, 2018).

Например, в датасете из фотографий практически исключено появление фотографий собаки, покрашенной в радужные цвета, или фотографий лица человека, которому на лоб приклеено фото другого человека. Такие изображения считаются OOD-данными. Также OOD-данными можно считать примеры с очень редкими значениями каких-либо признаков, которые имеют мало шансов попасть в обучающую выборку. Диагностика сдвига данных является важной практической задачей (Yang et al., 2021), а способность модели обобщаться на большее разнообразие примеров и ситуаций, чем те, что встречались при обучении, является открытой проблемой в машинном обучении и одной из метрик "интеллектуальности" модели (Shen et al., 2021; Goyal and Bengio, 2020; Battaglia et al., 2018; Chollet, 2019).

Рис. 1. Примеры некоторых типов не встречались при обучении, но на них желательна корректная работа модели, как минимум для защиты от атак, "обманывающих" модель.

Утечка данных

Утечкой данных (data leakage, или target leakage) называется ситуация, когда существует некий признак, который при обучении содержал больше информации о целевой переменной, чем при последующем применении модели на практике. Например, ID пациента может сильно коррелировать с диагнозом, но только в текущем датасете (который поделен на обучающую и тестовую часть). Модель, предсказывающая диагноз по ID, будет иметь высокую точность на тестовом датасете, но в целом очевидно, что в данной задаче такой способ предсказания некорректен и не будет хорошо работать на других данных. Утечка данных является частным случаем сдвига данных, поскольку зависимость ID $\to$ диагноз была в $P_{train}$ и $P_{test}$ , но ее не будет в $P_{usage}$ . Диагностировать утечку данных не всегда просто.

Еxample for this is KDD-Cup 2008 breast cancer prediction competition, where the patient ID contained an obvious leak. It is by no means obvious that removing this feature would leave a leakage-free dataset, however. Assuming different ID ranges correspond to different health care facilities (in different geographical locations, with different equipment), there may be additional traces of this in the data. If for instance the imaging equipment's grey scale is slightly different and in particular grey levels are higher in the location with high cancer rate, the model without ID could pick up this leaking signal from the remaining data, and the performance estimate
would still be optimistic (the winners show evidence of this in their report). (Kaufman et al., 2011)

Если удастся интерпретировать модель (хотя бы приблизительно), то мы получим дополнительную информацию, которая поможет надежнее оценить ее качество в условиях возможной утечки и сдвига данных.

Локальная интерпретация моделей

Вместо попыток интерпретировать модель целиком, что может быть очень сложно, мы можем рассмотреть задачу интерпретации ответа модели на конкретном, фиксированном примере x_0 . Например, если на данном изображении модель распознала собаку, то почему она распознала собаку? Какие части и свойства изображения повлияли на предсказание модели?

Local explanations have a distinct advantage over global explanations because by only focusing on a single sample they can remain more faithful to the original model. We anticipate that in the future local explanations will become foundational building blocks for many downstream tasks in machine learning. (Lundberg et al., 2019)

Для ответа на этот вопрос мы можем изменять x_0 и смотреть, как изменится при этом ответ модели, то есть мы изучаем зависимость $f(x_0 + \Delta x)$ от $\Delta x$ . При этом возможно удастся с хорошей точностью аппроксимировать эту зависимость простой функцией $g(\Delta x)$ . Такой подход называется локальной аппроксимацией модели в окрестности точки x_0 .

Например, рассчитав градиент $\nabla f(x)$ в точке x_0 мы узнаем, как изменится ответ при очень малых изменениях $\Delta x$ . При этом мы получаем локальную линейную аппроксимацию (в курсе высшей математики такая аппроксимация называется дифференциалом функции ). Такой подход используется, например, при расчете так называемых saliency maps в компьютерном зрении (Simonyan et al., 2013) - производных выходных значений сети по отдельным пикселям изображения. Но такая аппроксимация далеко не всегда адекватна:

Производная локальна и не говорит о том, как изменится ответ при существенных изменениях $\Delta x$ . Например, если один из признаков достиг состояния "насыщения", то есть значение данного признака более чем достаточно, чтобы сделать какой-то вывод о целевой переменной, то производная по нему почти равна нулю. Эффект будет лишь если мы сильно изменим данный признак.
В некоторых моделях (решающих деревьях) производная либо равна нулю, либо не существует.
Для бинарных признаков производная не всегда информативна, поскольку малое изменение признака ведет в "невозможную" область нецелого значения, в котором модель и не обязана работать корректно.

Есть и другие подходы к локальной интерпретации модели. В качестве $\Delta x$ мы можем рассматривать некий набор осмысленных, не бесконечно малых изменений входных данных - такой подход используется в методе LIME (Ribeiro et al., 2016).

Также мы можем интерпретировать не само предсказание f(x_0) , а одну из следующих величин:

Разницу между двумя предсказаниями $\Delta y = f(x_0) - f(x_{background})$
Разницу между текущим и усредненным предсказанием $\Delta y = f(x_0) - E[f(x)]$ .

Это означает, что мы пытаемся объяснить изменение в предсказании, вызванное изменением входных признаков (в первом случае) или появлением информации о входных признаках (во втором случае). При этом мы вычисляем вклад каждого признака в $\Delta y$ . Такой подход используется в методе SHAP (Lundberg and Lee, 2017).

Методы LIME и SHAP можно применить к любой модели машинного обучения, поскольку они никак не используют информацию о том, как устроена модель "изнутри", то есть являются model-agnostic методами (хотя существуют вычислительно эффективные реализации для конкретных видов моделей, такие как Tree SHAP).

Существуют также специфические способы интерпретации, позволяющие объяснить $\Delta y$ для конкретных типов моделей, например DeepLIFT (Shrikumar et al., 2017) и Integrated Gradients (Sundararajan et al., 2017) для нейронных сетей (т. е. дифференцируемых моделей). Эти методы в данном обзоре мы не будем рассматривать. Обзор других методов локальной интерпретации моделей можно найти, например, в Lundberg et al., 2019, раздел "Methods 7".

LIME: Local Interpretable Model-agnostic Explanations

LIME (Ribeiro et al., 2016) - это подход к интерпретации ответа модели f(x_0) на конкретном тестовом примере x_0 с помощью вычисления значений $f(x_0 + \Delta x)$ для некоторого конечного набора значений $\Delta x$ . Иллюстрация работы метода LIME приведена на рис. 2. Чтобы формально описать метод LIME, нам понадобится ввести ряд обозначений, которые мы будем использовать и в следующих частях обзора.

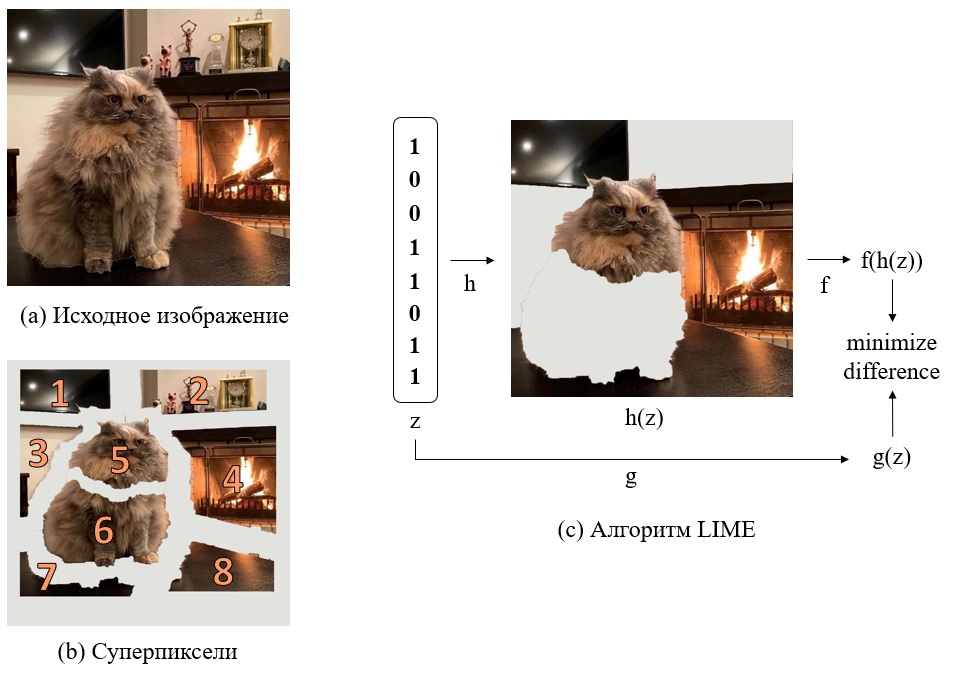
Мы интерпретируем модель на примере x_0 :

$f: X \to Y$ - исходная модель
$x_0 \in X$ - выбранный тестовый пример, предсказание на котором интерпретируется

Локальное упрощенное представление

Для примера x_0 вводим осмысленных, интерпретируемых изменений $\Delta_i$ . Например, для изображений таким изменением может быть удаление отдельного суперпикселя, то есть участка изображения с похожим содержимым и четкими границами (рис. 1b). Каждое изменение бинарно, то есть оно либо есть, либо нет. Соответственно, мы получаем 2^M различных вариантов $\Delta x$ . Наличие или отсутствие каждого из изменений можно описать числом 0 или 1: из этих чисел можно собрать бинарный вектор размерностью , который будем называть упрощенным представлением (рис. 1c).

$\{ \Delta_i \}_{i=1}^M$ - изменения примера
$z_i \in \{0, 1\}$ - индикатор изменения $\Delta_i$
$z \in \{0, 1\}^M$ - вектор упрощенного представления
$h: \{0, 1\}^M \to X$ - функция, преобразующая вектор упрощенного представления в $x_0 + \Delta x$

Например, на рис. 1 функция работает следующим образом: все "пристствующие" суперпиксели ( z_i = 1 ) рисуются без изменений. Все "отсутствующие" суперпиксели ( z_i = 0 ) заполняются белым цветом (либо, как вариант, усредненным цветом соседних суперпикселей). При этом $h([1, 1, \dots, 1]) = x_0$ , поскольку вектор из единиц означает отсутствие всех изменений. Фактически выбор функции равносилен выбору изменений $\Delta_i$ , то есть семантики упрощенного представления.

Функцию мы можем выбрать произвольно, но так, чтобы отдельные изменения $\Delta_i$ были интерпретируемы. При этом мы надеемся, что объяснить предсказание модели на x_0 можно интерпретировать, изучая, как влияют на ответ эти изменения. Конечно, функция может быть выбрана неудачно. Например, если модель определяет стиль фотографии как "ретро" при наличии оттенка "сепия", то изменения отдельных суперпикселей не помогут интерпретировать модель. Если $\Delta_i$ были выбраны неудачно, то всегда можно попробовать заново с другими изменениями $\Delta_i$ .

Для табличных данных мы можем в качестве $\Delta_i$ рассматривать замену одного из признаков на ноль, среднее или медианное значение по обучающему датасету.

Объясняющая модель

Теперь мы можем обучить модель предсказывать значение f(h(z)) по вектору упрощенного представления . При этом модель должна быть простой и интерпретируемой (поскольку смысл метода LIME в интерпретации). Например, это может быть линейная модель или решающее дерево. Чтобы обучить модель, нужно собрать обучающую выборку. Для этого нам потребуется получить ответ модели для разных (то есть для разных $x_0 + \Delta x$ , поскольку определяет $\Delta x$ ) и таким образом собрать обучающую выборку для модели .

$g: \{0, 1\}^M \to Y$ - объясняющая модель
$\big\{ z^{(i)}, f(h(z^{(i)})) \big\}_{i=1}^N$ - обучающая выборка для объясняющей модели

Максимально возможный размер обучающей выборки равен 2^M , но обычно велико, и приходится ограничиться перебором лишь некоторых значений . Авторы предлагают уделять основное внимание таким , которые близки к вектору из единиц: это соответствует небольшим изменениям в x_0 (чем больше нулей в , тем больше одновременных изменений x_0 мы рассматриваем). Введем функцию $\pi(z)$ , определяющую меру близости h(z) к x_0 , и назначим веса $\pi(z^{(i)})$ примерам из обучающей выборки.

$\pi: \{0, 1\}^M \to \mathbb{R}$ - мера близости к
$\big\{ w^{(i)} = \pi(z^{(i)}) \big\}_{i=1}^N$ - веса примеров из обучающей выборки

Примечание. В kernel SHAP, который мы рассмотрим в следующих разделах, в качестве $\pi$ берется функция, назначающая большие веса как векторам с большим количеством единиц, так и векторам с большим количеством нулей. Так мы акцентируем внимание в том числе на значениях с большим количеством нулей, то есть на отдельных интерпретируемых компонентах (напрмер, отдельных суперпикселях в случае изображений).

Для обучения модели осталось выбрать функцию потерь - например, среднеквадратичное отклонение. Эта функция будет сравнивать предсказания моделей и . Авторы предлагают также использовать "штраф за сложность" $\Omega(g)$ - например, количество ненулевых весов в линейной модели. Если в качестве функции потерь выбрано среднеквадратичное отклонение, то задача оптимизации формулируется следующим образом:

$\sum\limits_{i=1}^N w^{(i)} \Big( g(z^{(i)}) - f(h(z^{(i)})) \Big)^2 + \Omega(g) \to \min\limits_g$

В данной формуле мы считаем квадрат разности предсказаний объясняющей модели $g(z^{(i)})$ и исходной модели $f(h(z^{(i)}))$ , и считаем взвешенную сумму по обучающей выборке, используя веса $w^{(i)}$ . Кроме того мы прибавляем штраф за сложность объясняющей модели $\Omega(g)$ .

Таким образом, суть подхода LIME в том, что мы аппроксимируем предсказание модели в окрестности тестового примера x_0 более простой, легко интерпретируемой моделью , которая использует упрощенное представление . Например, если модель линейна, то каждому изменению $\Delta_i$ (например, суперпикселю в изображении) сопоставляется некий вес.

При этом мы надеемся, что такая аппроксимация адекватна, то есть наличие -го изменения линейно влияет на предсказание модели . В некоторых случаях это может оказаться совсем не так, и модель не сможет хорошо обучиться (функция потерь остенется высокой). Например, в случае изображений это может означать, что мы не можем линейно влиять на предсказание модели, удаляя отдельные суперпиксели. Возможно, модель ориентируется не на отдельные объекты, а на цвет изображения в целом. Тогда можно попробовать использовать другое упрощенное представление, элементами которого является информация об усредненном цвете изображения.

Работа алгоритма LIME не зависит от вида модели (нейронная сеть, решающие деревья и т. д.) и никак явно не использует информацию о том, как модель устроена "изнутри", то есть LIME является "model-agnostic" алгоритмом интерпретации.

Примеры и обсуждение

На рис. 3 мы видим объяснение предсказания сверточной нейронной сети Inception (Szegedy et al., 2014). Сначала мы рассматриваем выходной нейрон, соответствующий классу "Electric guitar", и пытаемся аппроксимировать значение на этом нейроне с помощью линейной модели , которая использует информацию о наличии или отстутствии суперпикселей ( бинарных признаков, где - количество суперпикселей). В результате для каждого суперпикселя мы получаем вес, то есть вклад этого суперпикселя в предсказание "Electric guitar", и выделяем суперпиксели с наибольшим весом. Далее повторяем тот же алгоритм для двух других выходных нейронов, соответствующих классам "Acoustic guitar" и "Labrador". Как можно видеть из примера, алгоритм LIME концептуально достаточно прост.

Рис. 3. Пример результатов, полученных с помощью метода LIME. Отмечены суперпиксели с наибольшими весами в линейной объясняющей модели.

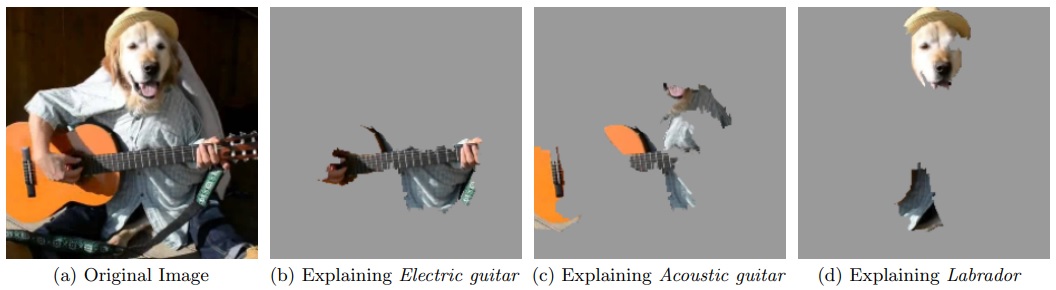
Работа алгоритма LIME определяется выбором набора изменений $\Delta_i$ , этот выбор осуществляется вручную и в каких-то случаях может быть неудачным. Поэтому LIME можно рассматривать как метод, в котором мы сначала формулируем гипотезу о том, как можно было бы объяснить предсказание модели, а затем проверяем ее.

Интересно было бы попробовать применить алгоритм LIME для интерпретации предсказаний человека на различных задачах. Такой подход мог бы дать лучшее понимание плюсов, минусов и границ применимости алгоритма.

Один из минусов заключается в том, что измененные примеры $x_0 + \Delta x$ могут быть неестественными, ненатуральными (например, изображение, в котором стерта часть суперпикселей). Модель , напротив, обучалась только на натуральных примерах, и чаще всего от нее не требуется корректная работа на ненатуральных примерах (не лежащих в многообразии исходных данных, в терминологии из книги Deep Learning, раздел 5.11.3). Хотелось бы проверять работу только для тех $x_0 + \Delta x$ , которые также выглядят натурально. Об этой проблеме мы еще поговорим в дальнейшем в разделе "Соблюдение границ многообразия данных".

Конечно, можно разрабатывать более эффективные способы интерпретации для конкретных предметных областей, но особенность LIME именно в том, что это очень общий подход, который может быть применен к широкому классу моделей. При этом многие детали в нем, в частности вид упрощенного представления, могут быть выбраны произвольно.

LIME-SP: объединение локальных интерпретаций в глобальную

Авторы также предлагают надстройку над алгоритмом LIME, называемую submodular pick (SP), которая может помочь интерпретировать модель в целом, а не только на конкретном примере. Для этого выбирается набор тестовых примеров, и каждый пример интерпретируется алгоритмом LIME, при этом к каждому примеру мы применяем одни и те же по смыслу изменения. Используя линейную модель , в результате мы получаем матрицу , строкой которой является номер примера, столбцом - позиция в векторе упрощенного представления, значением - вес данной позиции на данном примере.

Например, в случае модели, работающей с текстом и использующей bag-of-words, столбец матрицы будет соответствовать номер слова в словаре. Однако с суперпикселями так не получится, поскольку на каждом тестовом примере суперпиксели разные по смыслу.

Получив матрицу , мы можем рассчитать глобальный вес каждой позиции, найдя норму каждого столбца. Также мы можем попытаться выбрать небольшой набор строк матрицы такой, чтобы в этом наборе для каждого столбца хотя бы раз встретилось большое значение. Этот набор строк соответствует набору тестовых примеров, которых предположительно может быть достаточно для глобальной интерпретации модели.

SHAP: Shapley Additive Explanation Values

В данном разделе мы рассмотрим подход SHAP (Lundberg and Lee, 2017), позволяющий оценивать важность признаков в произвольных моделях машинного обучения, а также может быть применен как частный случай метода LIME.

Shapley values в теории игр

Теория игр - это область математики, изучающей взаимодействие (игру) между игроками, преследующими некие цели и действующими по неким правилам. Кооперативной игрой называется такая игра, в которых группа игроков (коалиция) действует совместно. С середины XX века (Shapley, 1952) известны так называмые Shapley values, которые позволяют численно оценить вклад каждого игрока в достижение общей цели.

Примечание. Понятие "игра" в данном случае может ввести в заблуждение. Обычно под игрой понимается противостояние двух и более сторон, здесь же речь пойдет скорее о кооперативном процессе, в котором каждый участник вносит вклад в общий результат.

Определение (Shapley values). Пусть существует характеристическая функция , которая каждому множеству игроков сопоставляет число - эффективность данной коалиции игроков, действующей совместно. Тогда Shapley value для каждого игрока - это число, рассчитываемое по достаточно простой формуле. Обозначим за $\Delta(i, S)$ прирост эффективности от добавления игрока в коалицию игроков :

$\Delta(i, S) = v(S \cup i) - v(S) \tag{1}$

Пусть всего есть игроков. Рассмотрим множество $\Pi$ всех возможных упорядочиваний игроков, и обозначим за $(\text{players before } i \text{ in } \pi)$ множество игроков, стоящих перед игроков в упорядочивании $\pi$ . Shapley value для игрока рассчитывается таким образом:

$\phi(i) = \cfrac{1}{N!} \sum\limits_{\pi \in \Pi} \Delta(i, (\text{players before } i \text{ in } \pi)) \tag{2}$

То есть мы считаем средний прирост эффективности от добавления -го игрока в коалицию игроков, стоящих перед ним, по всем возможным упорядочиваниям игроков (количество элементов суммы равно ).

Формула (2) задается аксиоматически, то есть есть формулируется ряд необходимых свойств и доказывается, что данное решение является единственным, которое им удовлетворяет. Поскольку $\Delta(i, S)$ не зависит от порядка игроков в , то можно объединить равные друг другу слагаемые и переписать формулу (2) в следующем эквивалентном виде:

$\phi(i) = \sum\limits_{S \subseteq \{1, 2, \dots, N\} \setminus i} \cfrac{|S|! (|N| - |S| - 1)!}{N!}\ \Delta(i, S) \tag{3}$

Формула (3) является взвешенной суммой по всем подмножествам игроков, не содержащих игрока , в которой веса принимают наибольшие значения при $|S| \approx 0$ или $|S| \approx |N|$ и наименьшие значения при $|S| \approx |N|\ /\ 2$ .

Shapley regression values

Shapley values можно применить в машинном обучении, если игроками считать наличие отдельных признаков, а результатом игры - ответ модели на конкретном примере . Shapley values применяются в машинном обучении еще с XX века (Kruskal, 1987).

Game-theoretic formulations of feature importance have become popular as a way to "explain" machine learning models. These methods define a cooperative game between the features of a model and distribute influence among these input elements using some form of the game's unique Shapley values. ... In this setting, the "players" are the features used by the model, and the game is the prediction of the model. (Kumar et al., 2020)

Shapley regression values (Lipovetsky and Conklin, 2001) позволяют оценить вклад каждого признака в ответ модели . Зафиксируем конкретный тестовый пример и обучающую выборку, и за характеристическую функцию множества признаков будем считать предсказание модели, обученной только на этих признаках:

$v(S) = f_S(x_S) \tag{4}$

Следовательно, $\Delta(i, S)$ - изменение в предсказании между моделью $f_{S \cup \{i\}}$ , обученной на признаках $S \cup \{i\}$ и моделью f_S , обученной на признаках :

$\Delta(i, S) = (f_{S \cup \{i\}}(x_{S \cup \{i\}}) - f_S(x_S)) \tag{5}$

Тогда вклад отдельных признаков в величину предсказания модели можно оценивать по формулам (2) и (3) . Отметим, что мы рассматриваем не вклад каждого признака в точность модели, а вклад каждого признака в величину предсказания модели на конкретном тестовом примере, что помогает интерпретировать это предсказание. Если модель предназначена для классификации, то в выходными значениями считаются logits - значения до операции softmax/sigmoid. Но можно рассматривать и вклад признаков в величину метрики качества, об этом см. в разделе "Диагностика сдвига данных с помощью SHAP loss values".

В целом есть некоторые проблемы в представлении признака как игрока. Дело в том, что для игрока существует лишь два состояния: либо он есть, либо его нет. Признак же существует как минимум в трех состояниях: два разных значения и неопределенное значение (отсутствие признака). В Shapley regression values сранивается текущее значение признака на примере с его полным отсутствием при обучении и тестировании.

Минусом такого подхода является высокая сложность вычислений: для расчета Shapley regression values нужно обучать модель на всех возможных подмножествах признаков, что в большинстве случаев невыполнимо. Однако мы можем намного быстрее посчитать приблизительное значение Shapley values, если будем считать не все элементы суммы (3) , а лишь некоторые, обладающие большими весами. Для этого мы можем использовать веса как вероятности при семплировании элементов суммы (аппроксимация семплированием, Shapley sampling values - Štrumbelj and Kononenko, 2014).

SHAP values

Можем ли мы аппроксимировать Shapley regression values, обучая всего одну модель на всех признаках? В этом случае нам нужно получать предсказание модели в случаях, когда многие из признаков имеют неопределенные значения. Большинство моделей не умеют работать с такими данными, что является проблемой.

Применим статистический подход и будем считать, что обучающие и тестовые данные взяты из некоторого распределения вероятностей. Пусть часть признаков в примере известны, часть пропущены. Обозначим за x_S известные признаки. В SHAP характеристическая функция множества признаков для примера и модели задается как условное мат. ожидание: v(S) = E[f(x) | x_S] . Данная формула означает, что за v(S) мы берем мат. ожидание предсказания на примерах $x^\prime$ , взятых из распределения данных, таких, что $x^\prime_S = x_S$ . О способе подсчета таких величин мы поговорим далее, но сначала дадим формальное определение SHAP values (Lundberg and Lee, 2017).

Определение (SHAP values). Пусть мы имеем модель , распределение данных и некий тестовый пример и хотим оценить важность текущих значений каждого признака по сравнению с их неопределенными значениями. SHAP (SHapley Additive exPlanation) values для признаков на примере - это Shapley values, рассчитываемые для следующей кооперативной игры:

Игроками являются признаки (наличие -го игрока означает текущее значение -го признака на примере , отсутствие -го игрока означает неопределенное значение -го признака - так же, как в Shapley regression values).
Характеристической функцией коалиции признаков является условное мат. ождидание по распределению данных.

Таким образом, алгоритм расчета SHAP values следует формулам (2) и (3) : для каждого возможного упорядочивания признаков мы берем все признаки, стоящие перед -м признаком (обозначим их за ) и считаем величину $\Delta_f(i, S) = E [f(x) | x_{S\ \cup\ i}] - E [f(x) | x_S]$ (о способе подсчета см. далее), после чего усредняем полученные значения по всем упорядочиваниям. Это означает, что SHAP values описывают ожидаемый прирост выходного значения модели при добавлении -го признака в текущем примере.

We propose SHAP values as a unified measure of feature importance. These are the Shapley values of a conditional expectation function of the original model. ... SHAP values attribute to each feature the change in the expected model prediction when conditioning on that feature. (Lundberg and Lee, 2017)

Наиболее важным свойством, которым обладают Shapley values, рассчитанные по формулам (2) и (3) , является состоятельность (consistency). Это свойство означает, что если (зафиксировав пример ) мы рассчитываем Shapley values для двух моделей и $f^\prime$ , и для любых , верно, что вклад признака при имеющемся множесте признаков в первой модели не меньше, чем во второй, то Shapley value этого признака в первой модели также не меньше, чем во второй:

$\textbf{If:}\ \ \forall S, i: \Delta_f(i, S) \geq \Delta_{f^\prime}(i, S) \quad \textbf{Then:}\ \ \phi_f(x) \geq \phi_{f^\prime}(x)$

Отличие SHAP values от Shapley regression values в том, что в последних характеристической функцией группы признаков x_S является значение $f_{x_S}(x_S)$ , а в SHAP values - E [f(x) | x_S] . В целом эти значения близки, так как $f_{x_S}$ как правило моделирует E[y|x_S] . Но Shapley regression values требуют многократного обучения модели и таким образом являются характеристикой обучаемой модели, тогда как SHAP values являются характеристикой обученной модели.

Проблемы и ограничения SHAP values

На практике рассчет SHAP values позволяет интерпретировать модель, выявлять скрытые проблемы в модели и данных и даже выполнять кластеризацию, что мы увидим далее в разделе "SHAP на практике". Однако такой подход имеет свои проблемы и ограничения. Проблемы SHAP можно поделить на три класса: вычислительные проблемы, проблемы ограниченной применимости и концептуальные проблемы.

Вычислительные проблемы. Определение SHAP не говорит о том, как именно рассчитывать E [f(x) | x_S] в условиях ограниченной по размеру выборки данных. Если бы мы имели прямой доступ к распределению $\mathcal{D}$ , неограниченные вычислительные ресурсы и могли бы бесконечно семплировать из $\mathcal{D}$ , то была бы возможна оценка E [f(x) | x_S] с любой точностью. Однако обычно мы имеем лишь обучающую и тестовую выборки, взятые из $\mathcal{D}$ . Их может быть недостаточно, чтобы надежно оценить . SHAP values можно искать либо введением различных упрощений (Kernel SHAP), либо для конкретных видов моделей (Tree SHAP), что мы рассмотрим в следующих разделах.

Проблемы ограниченной применимости. Shapley values являются достаточно гибким инструментом, который можно применять во многих случаях для оценки вклада "участников процесса" в результат. Но SHAP values не являются универсальным способом интерпретации как минимум потому, что выходные данные могут иметь сложный формат, а входные признаки могут быть не интерпретируемы.

Концептуальные проблемы возникают из вопроса о том, можно ли вообще SHAP values считать мерой важности признаков в модели? Дело в том, что SHAP values зависят не только от модели, но и от распределения данных, при этом даже признаки, которые никак не используются моделью, могут иметь ненулевые SHAP values. Об этом мы поговорим позже, так как этот вопрос требует отделного раздела.

Independent SHAP

Задачу оценки E [f(x) | x_S] , можно сильно упростить, если предположить, что наличие каждого признака линейно и независимо влияет на ответ модели. Тогда значения признаков, не входящих в , не зависят от x_S и друг от друга и линейно влияют на ответ, и E [f(x) | x_S] можно рассчитать, заменив пропущенные значения их мат. ожиданиями, которые можно приблизить средним значением по выборке данных. Обозначив пропущенные признаки за $\overline{S}$ , получим

$E [f(x) | x_S] \approx f([x_S, E[x_\overline{S}]])$

feature independence and model linearity are two optional assumptions simplifying the computation of the expected values (Lundberg and Lee, 2017)

В формуле стоит знак приблизительного равенства потому, что линейность и независимость - это лишь предположения: чем ближе они к истине, тем точнее аппроксимация. С помощью данной формулы мы можем рассчитать f(x_S) для любого подмножества признаков x_S , а значит получили возможность рассчитывать SHAP values на практике по формуле (3) , опционально применяя также аппроксимацию семплированием.

Не является ли линейность и независимость влияния признаков чрезмерно грубым упрощением? В некоторых случаях возможно является, но вспомним, что в методе LIME мы использовали такое же допущение, обучая линейную объясняющую модель . О связи SHAP и LIME мы поговорим далее.

Kernel SHAP

Авторы сопоставляют SHAP с несколькими появившимися в 2010-х годах методами интерпретации моделей машинного обучения, которые используют локальную аппроксимацию, в первую очередь с LIME, а также с layer-wise relevance propagation (Bach et al., 2015) и activation difference propagation (DeepLIFT) (Shrikumar et al., 2017), которые мы сейчас не будем рассматривать.

Как LIME, так и DeepLIFT рассматривают локальное упрощенное представление в виде вектора (где z_i = 0 означает наличие изменения $\Delta_i$ относительно примера x_0 ). В разделе, посвященном LIME, мы говорили о таком представлении и об объясняющей модели , аппроксимирующей f(h(z)) . Авторы SHAP рассматривают случай, когда объясняющая модель линейна (такие способы интерпретации авторы называют additive feature attribution methods):

$g(z) = \phi_0 + \sum\limits_{i=1}^M \phi_i z_i, \quad \phi_i \in \mathbb{R}, z_i \in \{0, 1\} \tag{4}$

Важным является случай, когда $\Delta_i$ означает удаление некоего признака из x_0 , то есть при z_i = 0 один из признаков в x_0 заменяется на неопределенное значение. В этом случае будем говорить, что z_i задает наличие признака. При этом постановка задачи становится эквивалентой той, на которой основан SHAP.

Вспомним, что в LIME при выборе линейной модели мы затем искали ее веса $\phi_i$ , но для этого мы должны были выбрать функцию потерь $\mathcal{L}$ , метрику сходства $\pi$ и штраф сложности $\Omega$ . Авторы SHAP выводят единственно возможные значения для $\mathcal{L}$ , $\pi$ и $\Omega$ такие, что полученные веса $\phi_i$ будут равны SHAP values, рассчитанным по формуле (3) , при обучении на всех возможных . Если же мы будем обучать не на всех , то полученные веса будут аппроксимировать $\phi_i(f, x_0)$ .

$\mathcal{L}$ - среднеквадратичное отклонение
$\Omega(g) = 0$
$\pi(z) = \cfrac{M-1}{{{M}\choose{|z|}}\ |z|\ (M-|z|)}$ , где ${M}\choose{|z|}$ - биномиальный коэффициент

Основное отличие от примера, предложенного авторами LIME (Ribeiro et al., 2016), состоит именно в $\pi(z)$ . Как мы видели в разделе "Объясняющая модель", $\pi(z)$ фактически является метрикой сходства между векторами, такие метрики часто называют ядрами (kernels), поэтому предложенная формула для $\pi(z)$ получила название Shapley kernel, а метод назван kernel SHAP.

Shapley kernel назначает большие веса примерам как с большим количеством единиц, так и с большим количеством нулей. Это означает, что мы обращаем основное внимание на примеры с (почти) максимальным и (почти) минимальным количеством компонентов (игроков). На рис. 4 показано отличие Shapley kernel от L2 distance и cosine similarity, которые предлагалось использовать в LIME.

Рис. 4. Shapley kernel в сравнении с L2 distance и cosine similarity.

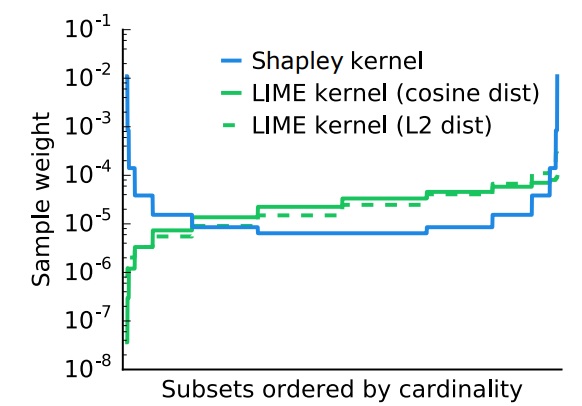
Формулировка метода Kernel SHAP не говорит о том, как именно рассчитывать или аппроксимировать E[f(x)|x_S] . В частности, можно использовать Independent SHAP (в python-библиотеке shap за это отвечает параметр algorithm объекта shap.KernelExplainer).

Таким образом,

Kernel SHAP - это способ приблизительного расчета суммы подсчетом не всех, а лишь части ее элементов
Independent SHAP - это способ приблизительного расчета элемента суммы , т. е.

Как видим, Kernel SHAP и Independent SHAP конкретизируют разные подзадачи и могут быть использованы совместно.

Tree SHAP

SHAP values основаны на условном мат. ождидании E [f(x) | x_S] , но не всегда понятно, как посчитать это значение (см. раздел "SHAP values"). Модели, основанные на решающих деревьях (градиентный бустинг, случайный лес) позволяют работать с произвольным количеством пропусков в данных, поэтому в таких моделях можно напрямую рассчитать значение E [f(x) | x_S] , сделав предсказание на признаках x_S .

Получить предсказание решающего дерева для примера с пропущенными значениями можно следующим образом. Рассмотрим пример и дерево , которое начинается разделяющим правилом, ведущим к двум поддеревьям D_1 и D_2 . Если данное правило основано на признаке, который известен, тогда на основе значения признака мы выберем нужное поддерево D_i(x) и возьмем его ответ: D(x) = D_i(x) . Если же признак пропущен, то в качестве ответа возьмем величину D(x) = (c_1 D_1(x) + c_2 D_2(x)) , где c_1 и c_2 - доли обучающих примеров, которые попали в первое и во второе дерево. Таким образом мы аппроксимируем значение E [f(x) | x_S] с помощью обучающей выборки.

SHAP values можно посчитать по формуле (3) , но количество слагаемых экспоненциально зависит от количества признаков, и алгоритм рассчета SHAP values в общем случае является NP-полным. Однако если ограничиться только решающими деревьями, то для расчета формулы (3) существует алгоритм c полиномиальной сложностью низкого порядка, предложенный в Lundberg et al., 2018 и реализованный в python-библиотеке shap.

SHAP на практике

Для подсчета SHAP values существует python-библиотека shap, которая может работать со многими ML-моделями (XGBoost, CatBoost, TensorFlow, scikit-learn и др) и имеет документацию с большим количеством примеров. С помощью бибилиотеки SHAP можно строить различные схемы и графики, описывающие важность признаков в модели и их влияние на ответ. Рассмотрим примеры из документации.

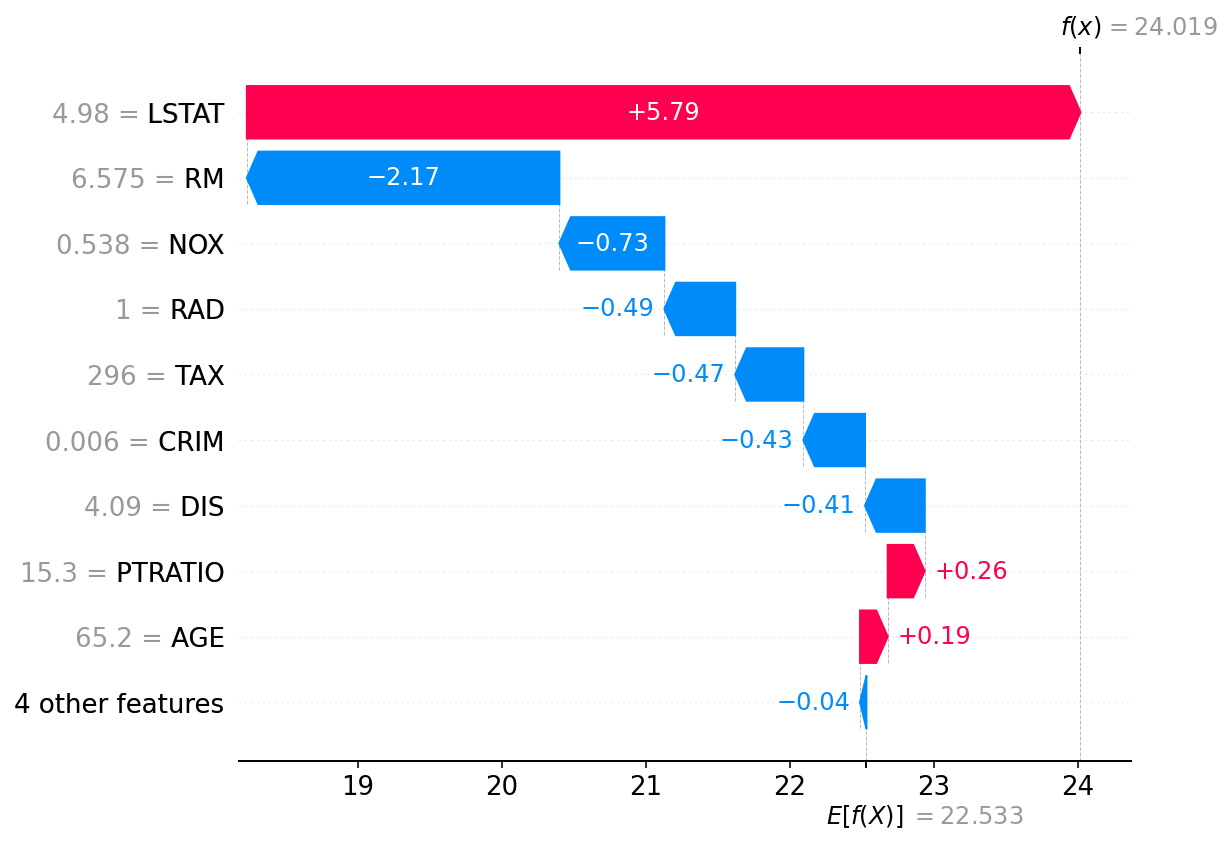
Waterfall plot

На рис. 5 показан waterfall plot, объясняющий предсказание на первом тестовом примере из датасета Boston housing. SHAP values получены с помощью метода Tree SHAP. Схема читается снизу вверх, и признаки упорядочены по возрастанию их SHAP values. Например, SHAP value -0.43 для признака CRIM (имеющего значение 0.006) говорит о том, что значение CRIM=0.006 на данном примере уменьшает величину предсказания модели, по сравнению с отсутствием признака CRIM, при произвольном наличии других признаков (см. "Shapley values в теории игр").

Summary plot

Рассчитав SHAP value для каждого признака на каждом примере с помощью shap.Explainer или shap.KernelExplainer (есть и другие способы, см. документацию), мы можем построить summary plot, то есть summary plot объединяет информацию из waterfall plots для всех примеров.

На рис. 6 summary plot построен для модели, обученной на датасете, описывающем влияние различных медицинских анализов на вероятность смерти в течение следущих 12 лет (Cox et al., 1997). Рисунок взят из Lundberg et al., 2019. SHAP values при этом получены с помощью метода Tree SHAP.

Каждая горизонтальная линия соответствует одному признаку, и на этой линии отмечаются точки, соответствующие тестовым примерам: кордината точки на линии соответствует SHAP value, цвет точки - значению признака. Если в каком-то участке линии не хватает места для всех точек, линия начинает расти в ширину. Таким образом, для каждого признака схема представляет собой слившееся множество точек, по одной точке для каждого примера

Слева на рис. 6 показана важность признаков, рассчитанная как средний модуль величины SHAP values для данного признака.

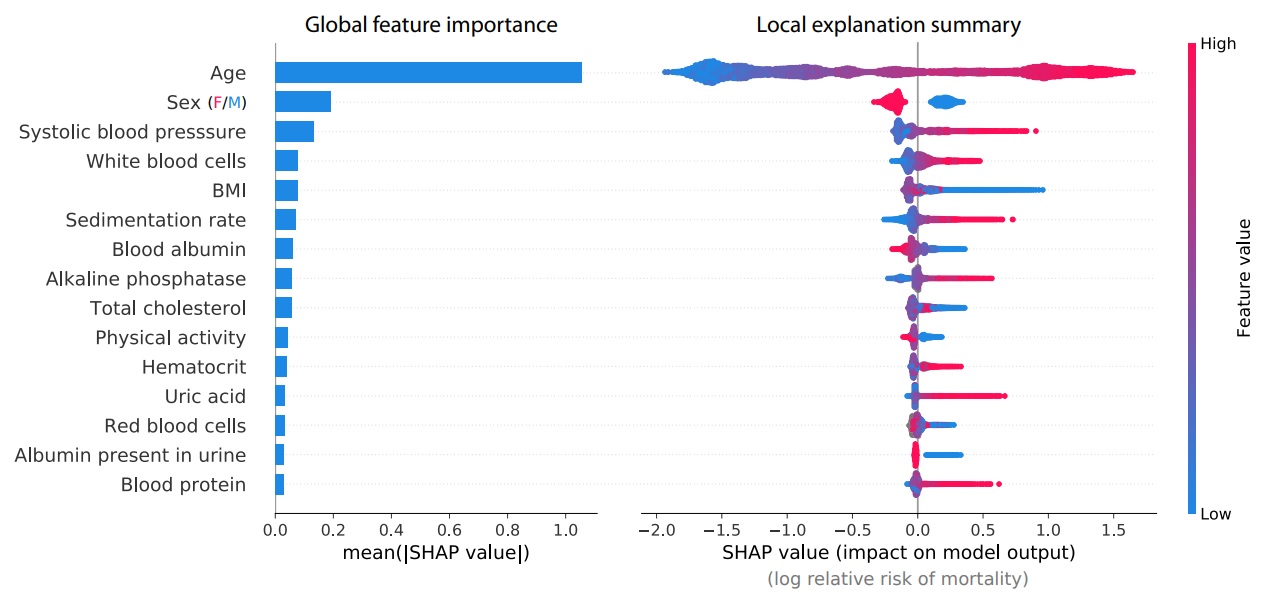
Очевидное влияние на риск смерти имеет возраст, а также пол (женщины среднестатистически живут дольше). Мы видим, что чем больше возраст (красный цвет), тем большее SHAP value (горизонтальная ось) назначается этому признаку. Большое значение SHAP value, в свою очередь, означает, что удаление этого признака (замена значения возраста на неопределенное) существенно уменьшит предсказанную вероятность смерти в течение 12 лет.

Можно также заметить, что большинство SHAP values, соответствующих медицинским анализам (строки 3 и далее), имеют либо оклонулевые, либо положительные значения SHAP values. Это означает, что есть много значений анализов, увеличивающих предполагаемый риск смерти (для данной модели), но нет таких значений, которые бы его сильно уменьшали.

Interestingly, rare mortality effects always stretch to the right, which implies there are many ways to die abnormally early when medical measurements are out-of-range, but not many ways to live abnormally longer. (Lundberg et al., 2019)

Одно из преимуществ SHAP summary plot по сравнению с глобальными методами оценки важности признаков (такими, как mean impurity decrease или permutation importance) состоит в том, что на SHAP summary plot можно различить 2 случая: (А) признак имеет слабое влияние, но во многих примерах, (Б) признак имеет большое влияние, но в немногих примерах.

SHAP summary plots avoid conflating the magnitude and prevalence of an effect into a single number, and so reveal rare high magnitude effects. (Lundberg et al., 2019)

Dependence plot

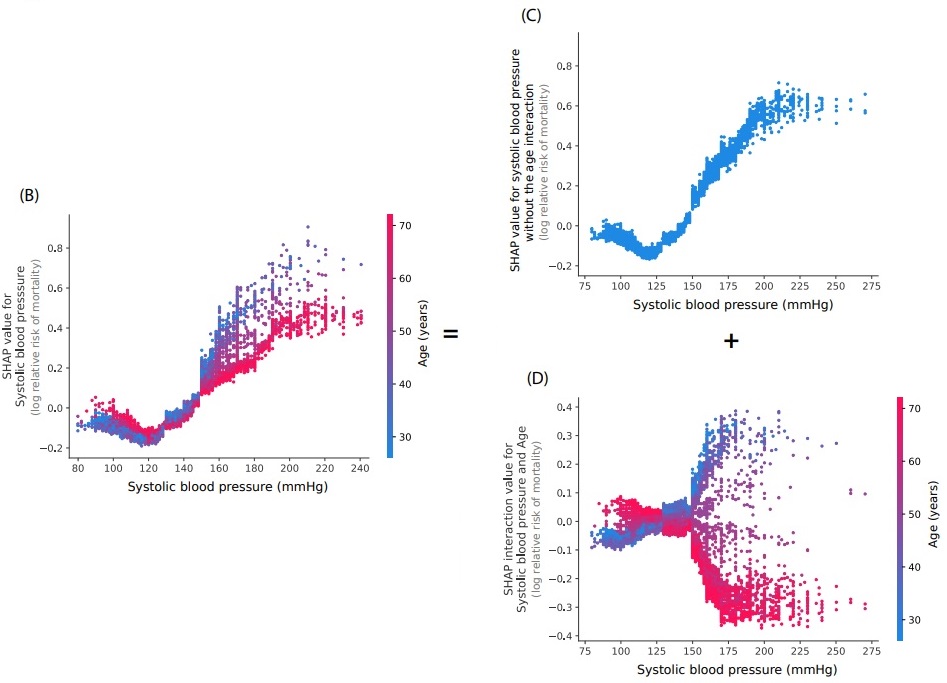
На рис. 7C мы видим совместное распределение SHAP value для признака Systolic blood pressure и значения этого признака по тестовому датасету. Фактически это та же самая информация, что показана в summary plot для этого признака. На рис. 7D показаны SHAP interaction values (их способ рассчета мы не рассматривали в этом обзоре) для пары признаков: Systolic blood pressure + Age. На рис. 7B показана схема (SHAP dependence plot), объединяющая информацию из схем на рис. 7C и 7D. Рисунки взяты из Lundberg et al., 2019.

Как можно видеть, совместное распределение на рис. 7B имеет "два хвоста". Для возраста 30-40 (синий цвет) систолическое давление 160+ mmHg повышает предсказанную вероятность смерти в течение 12 лет, тогда как для возраста 60-70+ это же давление является нормальным (соответствующим возрасту) и дополнительно не повышает вероятность смерти в течение 12 лет.

early onset high blood pressure is more concerning to the model than late onset high blood pressure (Lundberg et al., 2019)

Следует помнить, что при этом мы изучаем обученную модель, а не только данные. Модель может ошибаться, и тогда выводы о целевой зависимости, сделанные на основе SHAP values, тоже будут неверны.

Диагностика сдвига данных с помощью SHAP loss values

Cдвиг данных является серьезной проблемой в машинном обучении. Он может быть вызван недостаточным разнообразием обучающих данных, изменениями в методах расчета признаков и ошибками в их обработке после развертывания модели.

Deploying machine learning models in practice is challenging because of the potential for input features to change after deployment. It is hard to detect when such changes occur, so many bugs in machine learning pipelines go undetected, even in core software at top tech companies. (Lundberg et al., 2019).

Для диагностики сдвига данных можно использовать Shapley values, считая результатом кооперативной игры не предсказание модели, а функцию потерь. Тогда мы сможем определить, какие признаки вносят положительный или отрицательный вклад в точность модели.

В работе "Explainable AI for Trees" (Lundberg et al., 2019) авторы проводят следующий эксперимент. В качестве данных используется датасет, целевым признаком в котором является длительность процедуры анастезии перед операцией. Датасет содержит данные за 4 года (2185 признаков и ок. 147000 пациентов). Данные за первый год используются для обучения, данные за следующие три года - для тестирования (симуляции работы системы по разначению). Отметим, что это не временной ряд: каждый пример независим.

График метрики качества на тестовых данных (в зависимости от даты) показан на рис. 8. Такие графики используют для мониторинга качества работы системы. Метрика качества на обучающих данных (первый год) намного лучше, что естественно.

Рис. 8. Метрика качества на обучающих и тестовых данных в датасете "hospital procedure duration".

На каждом тестовом примере можно рассчитать SHAP loss values, считая игроками наличие признаков, а характеристической функцией набора признаков - точность предсказания на данном примере. Поскольку каждый тестовый пример соответствует определенной дате, то мы можем построить для каждого признака график зависимости Shapley loss values от даты. На Рис. 9 показаны такие графики для трех бинарных признаков (цветом обозначено значение признака).

Рис. 9. Мониторинг SHAP loss values обнаруживает проблемы, не видимые по графику метрики качества, в датасете "hospital procedure duration".

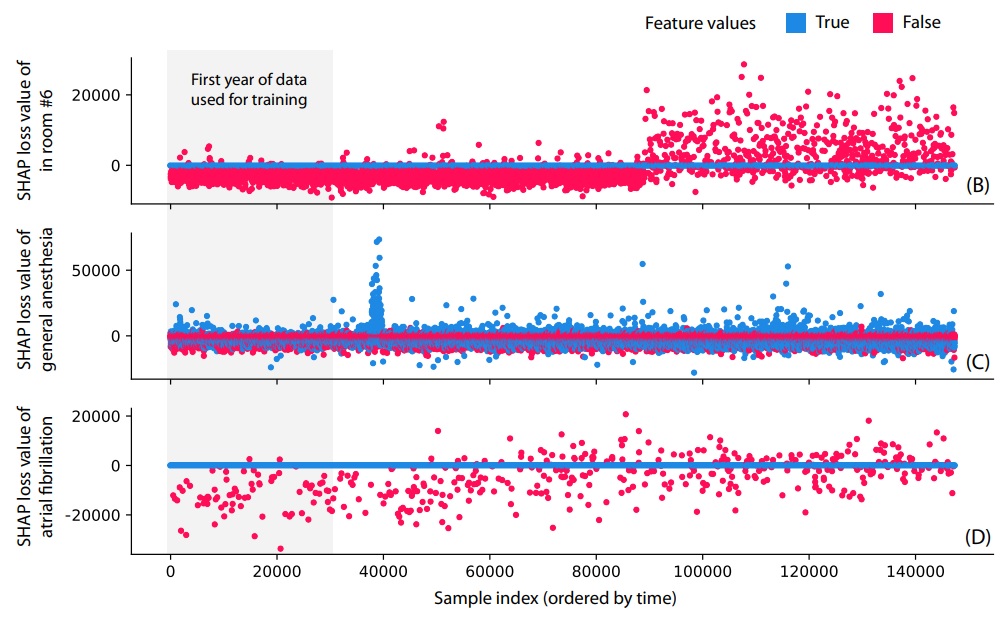
Первый признак "in room #6" означает, что процедура проводилась в комнате номер 6. При обучении этот признак понижал ошибку предсказания времени процедуры, но при симуляции работы по назначению с какого-то момента стал резко повышать ошибку, то есть наличие этого признака стало вредным. Причина кроется в том, что в коде обработки признаков была допущена ошибка: перепутаны номера комнат 6 и 13. Данная ошибка была допущена исследователями намеренно, чтобы показать эффективность SHAP loss values в обнаружении подобных проблем. При этом на графике функции потерь этой проблемы не видно, так как она затрагивает лишь небольшой процент данных.

Следующие две проблемы, напротив, были ненамеренными и обнаружены случайно. Признак "general anasthesia" в определенный момент резко снижал точность предсказания. Как выяснилось, проблема была связана с ошибкой в конфигурации электронного оборудования.

На признаке "atrial fibrillation" виден дрейф значений SHAP loss values: со временем этот признак становится все менее полезным, и в итоге начинает понижать точность предсказания времени процедуры. Как выяснилось, это вызвано изменениями в длительности процедуры абляции фибрилляции предсердий, которая связана с изменениями в технологиях и персонале.

Supervised-кластеризация данных с помощью SHAP

Из SHAP values можно составить SHAP-вектор для каждого обучающего или тестового примера. Lundberg et al., 2018 заметили, что SHAP-векторы можно использовать для кластеризации данных намного эффективнее, чем вектора исходных признаков.

Задача кластеризации данных достаточно нетривиальна. Как правило, мы не можем выполнить кластеризацию просто на основе евклидова расстояния между векторами признаков, так как признаки различаются по важности, имеют разный масштаб, и некоторые признаки могут дублировать друг друга.

Элементы SHAP-вектора соответствуют отдельным признакам, но при этом каждый элемент SHAP-вектора представлен в одной и той же шкале. При этом величина SHAP value означает важность признака (в контексте задачи предсказания целевого признака). Исходя из этого, можно выполнять supervised-кластеризацию в пространстве SHAP-векторов.

The distance metric does not account for the discrepancies among the units/meaning of features (e.g., weight vs. age), and there
is no way for an unsupervised approach to know which features are relevant for an outcome of interest, and so should be weighted more strongly. We can address both of these limitations by using local explanation embeddings to embed each sample into a new "explanation space." If we run clustering in this new space, we will get a supervised clustering where samples are grouped together based on their explanations. Supervised clustering naturally accounts for the differing units of various features, only highlighting changes that are relevant to a particular outcome. ... Analogously, we can also run PCA on local explanation embeddings... (Lundberg et al., 2019)

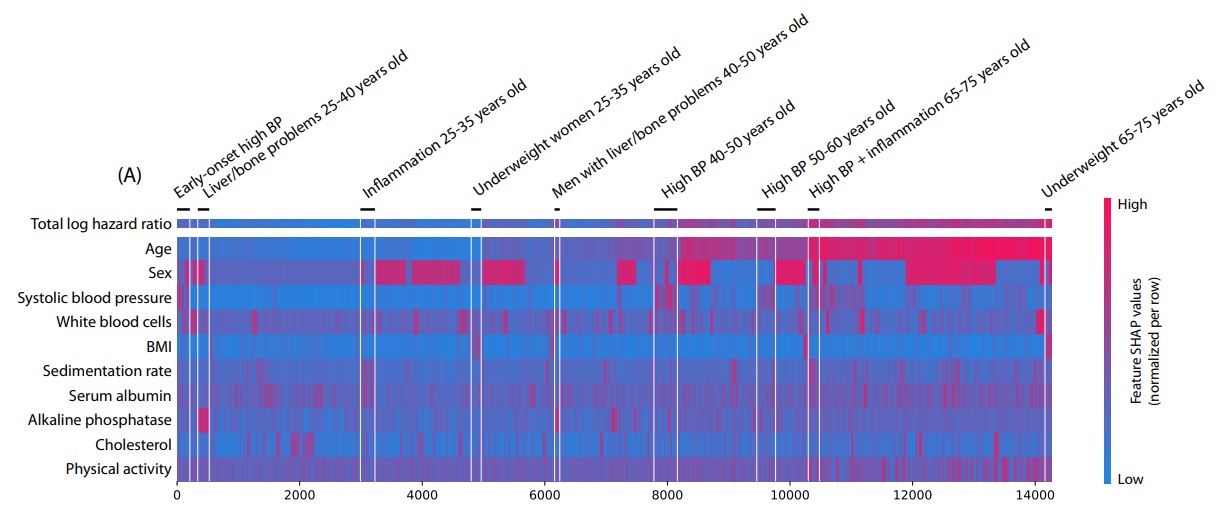
На рис. 10 показана кластеризация с помощью SHAP на датасете, описывающем риск смерти в течение 12 лет на основе медицинских анализов (об этом датасете см. также раздел "Summary plot"). Каждый столбец представляет собой SHAP-вектор для одного пациента, и эти векторы упорядочены (локально) по сходству друг с другом с помощью алгомеративной иерархической кластеризации и (глобально) по значению целевого признака, объединяясь в кластеры людей со сходной симптоматикой.

Рис. 10. Кластеризация данных с помощью SHAP values.

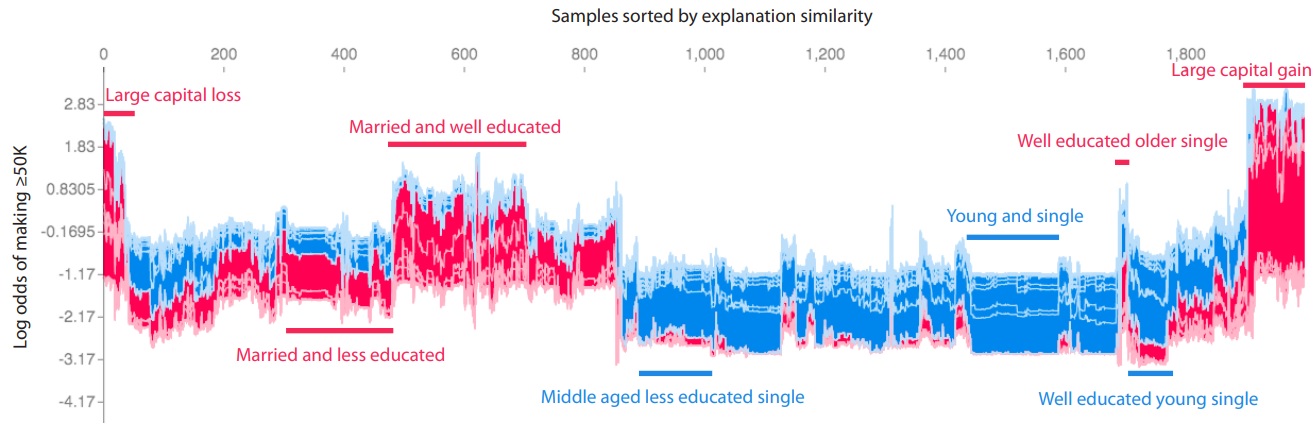
Другой пример из Lundberg et al., 2018 изображен в трехмерном формате (рис. 11). В данном случае показаны примеры из датасета, в котором целевой переменной является вероятность месячного заработка больше $50К. Примеры здесь тоже кластеризованы с помощью их SHAP-векторов ("sorted by explanation similarity"), то есть мы ищем группы примеров, предсказания на которых объясняются схожим образом. Полученным кластерам даны текстовые описания.

Рис. 11. Еще один пример кластеризации данных с помощью SHAP values.

Проблемы SHAP values

Можно ли SHAP values считать адекватной мерой важности признаков в модели? Как мы увидим далее, SHAP values может быть не равно нулю даже для тех признаков, которые никак не используются в модели.

Если рассуждать более глобально, то проблема SHAP values в том, что выбор характеристической функции v(S) = E [f(x) | x_S] является не единственно возможным, существуют и другие варианты, и каждый вариант может быть по-своему хорош или плох в разных ситуациях.

the correct way to connect a machine learning model to a coalitional game has been a source of controversy (Chen et al., 2020)

SHAP values в условиях взаимной зависимости признаков

Ранее мы рассматривали определение SHAP values и видели, что значение E [f(x) | x_S] может либо точно рассчитываться (в Tree SHAP для решающих деревьев), либо аппроксимироваться (в Independent SHAP).

Tree SHAP рассчитывает непосредственно SHAP values: v(S) = E [f(x) | x_S] , аппроксимируя их с помощью обучающей выборки. При этом значение v(S) зависит не только от модели , но и от распределения данных. Таким образом, SHAP values являются характеристикой не только модели, а объединенной системы "модель + данные". На разных распределениях данных SHAP values для одной и той же модели может оказаться разной.

Пусть два признака и коррелируют, при этом модель использует для предсказания только признак . Признак влияет на мат. ожидание признака , а отсюда и на мат. ожидание ответа модели, следовательно признак может иметь ненулевое значение SHAP value. Этот признак никак не используется моделью, но он позволяет предсказывать значения других признаков и таким образом влияет на ожидаемый ответ модели. Более подробный пример можно найти в Janzing et al., 2019, см. Example 1. В целом если два признака всегда равны друг другу, то SHAP values для них тоже будут равны, даже если модель использует лишь один из этих признаков.

Таким образом, не используемые моделью признаки могут иметь ненулевые SHAP values, потому что распределение данных таково, что эти признаки позволяют предсказать ожидаемый ответ модели. Поэтому интерпретировать SHAP values как важность признаков в модели не всегда корректно.

For instance, the popular SHAP algorithm’s formulation may give substantial attributions to features that play no role in the model (Merrick and Taly, 2019)

Say, in the context of an analysis of fairness, we require that a certain feature play no role in the prediction model, and indeed, it does not. If we use CES [Conditional Expectations Shapley - SHAP], it may still be assigned significant attribution, leading us to incorrectly believe that the function is sensitive to the variable. (Sundararajan and Najmi, 2019)

Independent SHAP аппроксимирует SHAP values следующим образом: $v(S) = f([x_S, E[x_\overline{S}]])$ . При этом зависимость v(S) от распределения данных сохраняется, но в Independent SHAP те признаки, которые не используются моделью, всегда будут иметь нулевые SHAP values. С другой стороны, игнорирование зависимости признаков друг от друга в Independent SHAP может привести к тому, что определенные сочетания признаков $[x_S, E[x_\overline{S}]]$ будут необычны или вовсе некорректны, что означает, что мы будем изучать предсказания модели на данных за пределами обучающего распределения (out-of-distribution).

Соблюдение границ многообразия данных

Множество реальных данных как подмножество часто называют многообразием данных (Carlsson, 2009; Fefferman et al., 2013). Это не обязательно многообразие в математическом смысле, но что-то общее между ними есть. В математике многообразие - это подмножество некоего пространства, являющееся локально евклидовым, то есть в нем можно ввести локальные координаты и, изменяя их, "путешествовать" по многообразию. Имея набор данных с большим количеством признаков часто можно предположить, что все значения признаков обусловлены небольшим количеством незавимых факторов (см. факторный анализ). Изменяя значения этих факторов, можно "путешествовать" по многообразию данных, не выходя за его пределы. В данных, как правило, есть случайный шум, поэтому данные можно считать лежащими не на многообразии, а в окрестности многообразия.

Хотя у термина «многообразие» есть строгое математическое определение, в машинном обучении его используют менее формально для обозначения связного множества точек в пространстве высокой размерности, которое можно хорошо аппроксимировать, вводя в рассмотрение лишь небольшое число степеней свободы, или измерений. Каждое измерение соответствует локальному направлению изменения. (Deep Learning, раздел 5.11.3)

В предыдущем разделе мы рассматривали проблему ненулевых SHAP values для признаков, которые не используются в модели. Часто эту проблему рассматривают под таким углом (Chen et al., 2020): при локальной интерпретации модели в окрестности примера x_0 стоит ли ограничиться изучением поведения модели в рамках многообразия данных (Tree SHAP), или нужно также рассматривать и поведение модели на таких изменениях x_0 , которые дают нереалистичные примеры (Independent SHAP)?

On one side, many argue that perturbing features independently reveals the functional dependence of the model, and is thus true to the model. However, independent perturbation of the data can create unrealistic or invalid sets of model input values. Thus, on the other side, researchers argue that one should perturb features while staying on the data manifold, and so be true to the data. (Wang et al., 2020)

Справедливости ради надо отметить, что не всегда следует избегать выхода за пределы многообразия обучающих данных. Конечно, при этом мы можем получить совершенно невозможные сочетания признаков, и на таких сочетаниях от модели не требуется корректная работа. За пределами многообразия реальных данных модель может вести себя как угодно (рис. 12), и ее интерпретация в этих областях неинформативна. Но с другой стороны, существует проблема сдвига данных, когда распределение данных меняется.

Рис. 12. Модель может хорошо работать в пределах распределения данных, но вести себя необычно за его пределами. В данном примере один из "хвостов" распределения данных не попал в обучающую выборку из-за ее ограниченного разнообразия, из-за чего модель неверно работает в этой области (проблема сдвига данных). Однако есть такие области, в которых поведение модели нас вообще не интересует, так как таких данных не бывает.

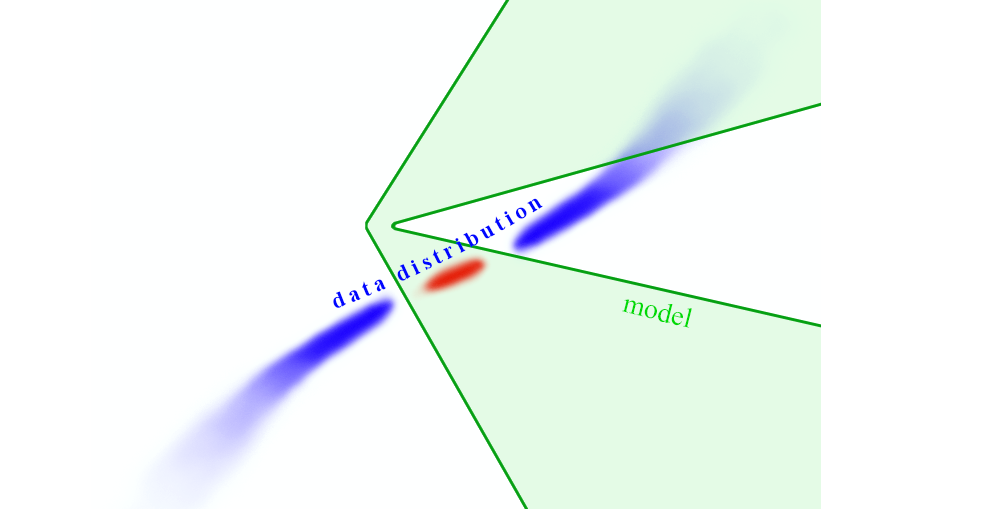
Резюме. Выйдя пределы многообразия обучающих данных, мы можем получить нереалистичные или некорректные данные, но оставаясь на многообразии, мы можем получить сильную взаимосвязь признаков, что создает сложности в оценке их независимого влияния на предсказания. Более подробно об этой проблеме можно почитать в статье "True to the Model or True to the Data?" (Chen et al., 2020).

Shapley Flow

Shapley Flow (Wang et al., 2020) - это еще один метод интерпретации предсказания модели на конкретном примере, являющийся обобщением метода SHAP. Его можно применять тогда, когда о многообразии данных известна какая-то информация. Рассмотрим алгоритм действий в методе Shapley Flow.

Программную реализацию Shapley Flow можно найти в данном репозитории, в нем же есть туториал.

Использование метода Shapley Flow

Шаг 1. Строится граф причинно-следственных связей (causal graph) во входных данных (рис. 13). Вершинами графа являются признаки, направленные ребра обозначают наличие причинно-следственной связи. К этому графу добавляется еще одна вершина - предсказание модели. Этот граф используется как входные данные для алгоритма Shapley Flow.

Рис. 13. Граф причинно следственных связей в данных. Также к графу добавляется вершина, из которой идут ребра во все остальные вершины: эта вершина означает случайные эффекты, она не показана на рисунке для лучшей читаемости. Данный граф причинно-следственных связей является упрощенным и используется лишь для иллюстрации работы метода.

Шаг 2. Выбирается два примера: x_0 и $x_{background}$ . Метод Shapley Flow нацелен на интерпретацию различия в предсказаниях между этими примерами, основываясь на различии исходных признаков, то есть интерпретируется $\Delta y = f(x_0) - f(x_{background})$ . Например, если модель работает с медицинскими данными, то в качестве $x_{background}$ можно взять типичные значения анализов для какой-то болезни. Также авторы упоминают о том, что Shapley Flow позволяет использовать в качестве $x_{background}$ одновременно несколько значений или распределение значений.

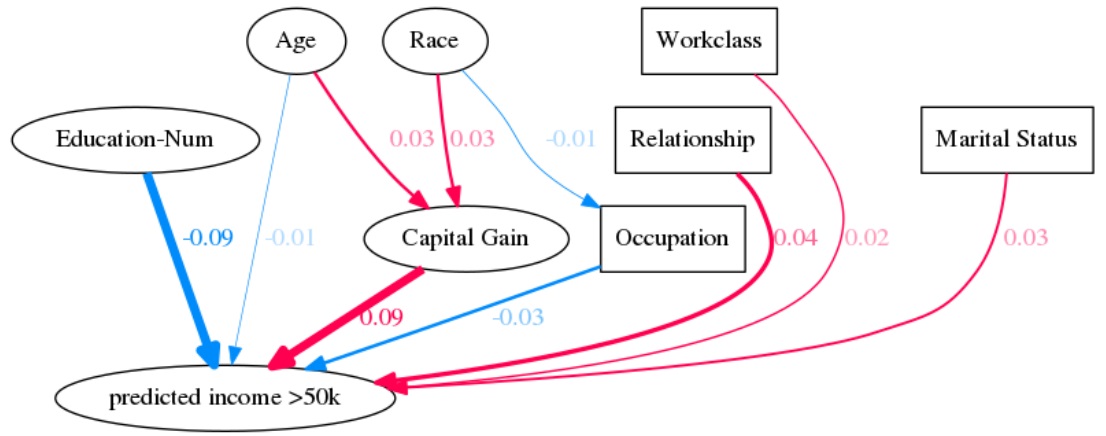
Шаг 3. Алгоритм Shapley Flow оценивает вклад в $\Delta y$ для каждого ребра в графе. Вклад каждой вершины (признака) при этом считается как сумма вкладов выходящих из нее ребер. Пример результата показан на рис. 14 (показаны 10 ребер с наибольшими по модулю вкладами).

Рис. 14. Иллюстрация работы метода Shapley Flow. Показаны 10 ребер с наибольшими по модулю вкладами.

Принцип работы метода Shapley Flow

Здесь мы не будем углубляться в детали метода Shapley Flow, но рассмотрим общую идею. Согласно авторам метода Shapley Flow, дилемма "interventional" против "conditional" интерпретации связана с выбором "границ объяснения" (boundary of explanation). Границей объяснения называется деление причинно-следственного графа на две части и таким образом, что ребра могут идти из в , но не могут идти обратно. При этом можно рассматривать как модель, а - ее входные данные.

На рис. 15 показана простая модельная задача (Pearl and Russell, 2000). В задаче есть пять переменных:

- сезон года
- идет ли дождь?
- включен ли разбрызгиватель воды?
- сыро ли на улице?
- сколько ли на улице?

Красными стрелками показаны причинно-следственные статистические связи между признаками. С определенной долей вероятности можно утверждать следующее:

$X_1 \to X_3$ : если сезон сухой, то разбрызгиватель включен
$X_1 \to X_2$ : если сезон влажный, то идет дождь
$X_3 \to X_4$ : если разбрызгиватель включен, то покрытие мокрое
$X_2 \to X_4$ : если идет дождь, то покрытие мокрое
$X_4 \to Y$ : если покрытие мокрое, то на улице скользко

Модель предсказывает значение , используя все четыре переменные X_1, X_2, X_3, X_4 . При этом модель делает предсказание только на основе X_3 и X_4 (которые коррелируют), но это заранее не известно. Нужно определить, от чего зависит ответ модели . При этом граф причинно-следственных связей известен.

На рис. 15 (a-c) проиллюстрирована работа трех методов: Independent SHAP, Assymetric Shapley values (ASV, Frye et al., 2019) и Shapley Flow. Метод Independent SHAP относится к классу "inverventional" (см. предыдущий раздел) и не учитывает границы многообразия данных: признаки в нем считаются независимыми. Этот метод назначит ненулевой вклад только признакам X_3 и X_4 . Его можно рассматривать как "interventional" по отношению к "границе объяснения" F_1 , то есть вершины, имеющие непосредственные связи с F_1 , изменяются независимо, и таким образом изучается поведение модели.

Рис. 15. Сравнение методов SHAP, Assymetric SHAP и Shapley Flow на модельной задаче.

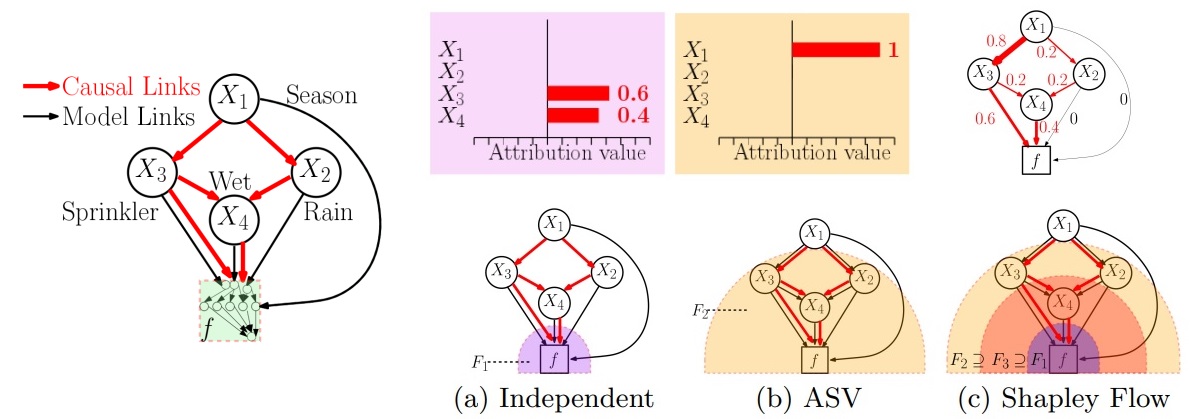
Метод Assymetric Shapley values является обобщением SHAP, которое позволяет использовать информацию о причинно-следственных связях в исходных данных. Его можно рассматривать как "interventional" по отношению к "границе объяснения" F_2 , то есть вершины, имеющие непосредственные связи с F_2 (а это только вершина X_1 ), изменяются независимо. Этот метод назначит ненулевой вклад только вершине X_1 .

Авторы Shapley Flow стремятся объединить оба подхода. При этом рассматриваются все возможные "границы объяснения", и важность вклад назначается не вершинам, а ребрам. Таким образом, во-первых мы видим признаки, которые непосредственно влияют на ответ модели ( X_3 и X_4 ), а во-вторых видим признаки, которые влияют косвенно ( X_1 ) и тем самым могут объяснить наличие этих значений в данном примере.

Алгоритм Shapley Flow, как и Shapley values, задается аксиоматически, и доказывается единственность решения. Если SHAP основан на Shapley values, то Shapley Flow основан на Owen values - расширении понятия Shapley values. Более детальное описание этого метода можно найти в Wang et al., 2020.

Заключение

Интерпретация моделей машинного обучения не является простой задачей, поэтому существенная часть этого обзора была посвящена различным проблемам при применении методов LIME и SHAP.

В LIME мы пытаемся найти локальную аппроксимацию модели (обычно линейную), но получившаяся аппроксимация может быть неточной и иногда вводить в заблуждение.

SHAP направлен на интерпретацию моделей, но сами результаты этого метода не всегда легко интерпретировать. SHAP values не имеют простого и интуитивно понятного определения, и при этом имеют разновидности (Tree SHAP, Independent SHAP, Kernel SHAP, Deep SHAP), которые существенно различаются:

Tree SHAP позиционируется как "high-speed exact algorithm", однако именно в нем результаты зависят от распределения данных, что контринтуитивно. При этом признаки, которые вообще не используются моделью, могут иметь ненулевые SHAP values.
Independent SHAP не имеет такой проблемы, но работает намного медленнее и иногда оценивает работу модели на некорректных сочетаниях признаков.

Несмотря на это, SHAP values могут быть очень полезны и могут помочь не только в интерпретации предсказаний, но и в отладке работы модели в условиях сдвига данных, а также в кластеризации данных.

Shapley Flow является наиболее общим, но и наиболее сложным методом, в котором требуется строить граф причинно-следственных связей в данных. Этим по-видимому и вызвана его пока что малая распространенность на практике.

Список источников

Akhtar and Mian, 2018. Threat of Adversarial Attacks on Deep Learning in Computer Vision: A Survey.
Bach et al., 2015. On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation.
Battaglia et al., 2018. Relational inductive biases, deep learning, and graph networks.
Brendel and Bethge, 2019. Approximating CNNs with Bag-of-local-Features models works surprisingly well on ImageNet.
Brown et al., 2017. Adversarial Patch.
Carlsson, 2009. Topology and Data.
Chen et al., 2020. True to the Model or True to the Data?
Chollet, 2019. On the Measure of Intelligence.
Cox et al., 1997. Plan and operation of the NHANES I Epidemiologic Followup Study, 1992.
Goodfellow et al., 2016. Deep Learning.
Fefferman et al., 2013. Testing the Manifold Hypothesis.
Goyal and Bengio, 2020. Inductive Biases for Deep Learning of Higher-Level Cognition.
Janzing et al., 2019. Feature relevance quantification in explainable AI: A causal problem.
Kaufman et al., 2011. Leakage in Data Mining: Formulation, Detection, and Avoidance.
Kruskal, 1987. Relative Importance by Averaging Over Orderings.
Kumar et al., 2020. Problems with Shapley-value-based explanations as feature importance measures.
Li et al., 2021. Interpretable Deep Learning: Interpretation, Interpretability, Trustworthiness, and Beyond.
Linardatos et al., 2020. Explainable AI: A Review of Machine Learning Interpretability Methods.
Lundberg and Lee, 2017. A Unified Approach to Interpreting Model Predictions.
Lundberg et al., 2018. Consistent Individualized Feature Attribution for Tree Ensembles.
Lundberg et al., 2019. Explainable AI for Trees: From Local Explanations to Global Understanding.
Lipovetsky and Conklin, 2001. Analysis of Regression in Game Theory Approach.
Merrick and Taly, 2019. The Explanation Game: Explaining Machine Learning Models Using Shapley Values.
Pearl and Russell, 2000. Bayesian networks.
Ribeiro et al., 2016. "Why Should I Trust You?": Explaining the Predictions of Any Classifier.
Shapley, 1952. A Value for N-Person Games.
Shen et al., 2021. Towards Out-Of-Distribution Generalization: A Survey.
Shrikumar et al., 2017. Learning Important Features Through Propagating Activation Differences.
Simonyan et al., 2013. Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps.
Štrumbelj and Kononenko, 2014. Explaining prediction models and individual predictions with feature contributions.
Szegedy et al., 2014. Going Deeper with Convolutions.
Sundararajan et al., 2017. Axiomatic Attribution for Deep Networks.
Sundararajan and Najmi, 2019. The many Shapley values for model explanation.
Wang et al., 2020. Shapley Flow: A Graph-based Approach to Interpreting Model Predictions.
Yang et al., 2021. Generalized Out-of-Distribution Detection: A Survey.

Данный обзор первоначально размещен на сайте generalized.ru, где вы можете найти и другие обзоры.