Эту вещь я хотел сделать с детства, но тяжело такое имплементировать, когда у тебя что на ЕС-1022, что на СМ-4 не хватает памяти. Сейчас такие вещи делаются играючи.
Итак, засеем бесконечное поле в игре "Жизнь" клеточками с вероятностью p от 0 до 1. Какова будет плотность популяции клеток после N ходов?
Технические детали: я стащил код отсюда и менял его под себя. "Бесконечное" поле замкнуто на тор, чтобы уменьшить краевые эффекты. Размер поля обычно брался 1000x1000. И да, python это плохой выбор для таких вычислений - вот тут я вижу как достигают скорости 2.5 миллиона evaluated cells per second на CPU и 25 миллионов - на GPU.
Первые два хода
Первый ход можно вычислить аналитически. Вероятность того, что вокруг клетки находятся n (от 0 до 8) заполненных клеток при вероятности p составляет:
Вероятность рождения новой жизни в пустой клетке, если вокруг ровно три соседа:
а смерти
Новая плотность
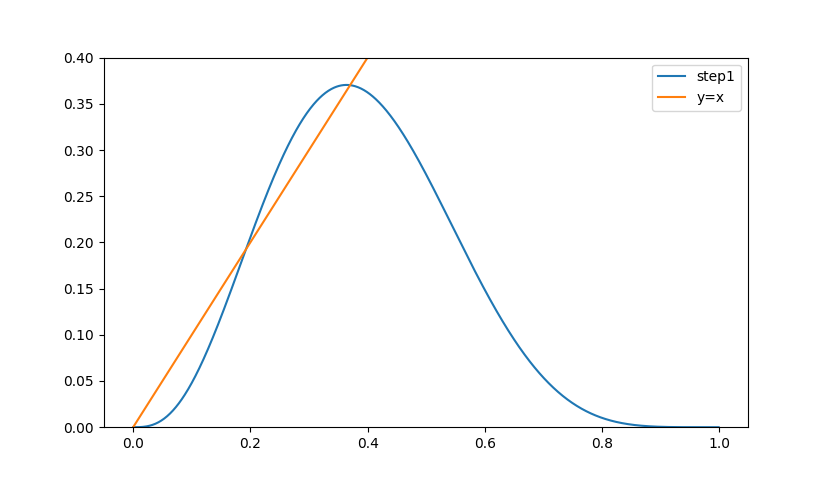
Интересно, что кривая имеет две фиксированные точки (x=y), и на небольшом промежутке начальная плотность даже увеличивается, достигая максимума в 0.37. Численный эксперимент согласуется с этим результатом:
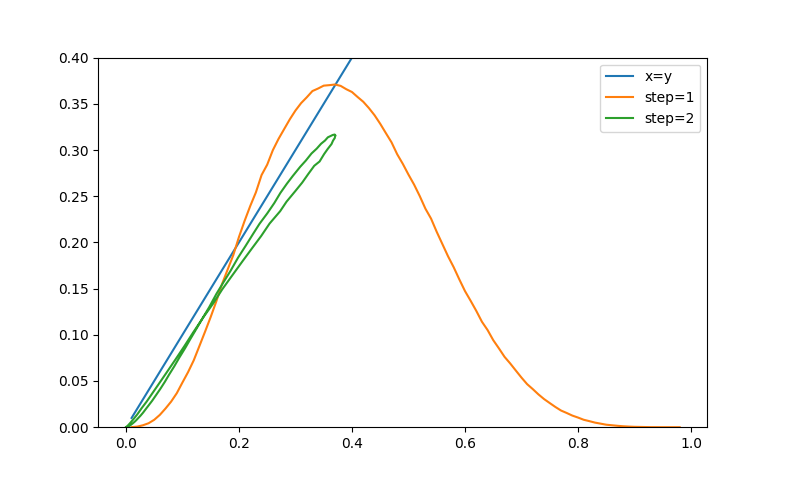
После первого шага мы вновь получаем хаос, хаос другой плотности (p1). Этот хаос отличается от первичного хаоса, и правила первого шага ко второму не применимы. Конечно, для второго шага мы тоже могли бы написать аналитическое выражение, но оно такое огромное, что это практически нереально.
Интересно построить график, где на x находится p1 (плотность после первого шага), а на y - p2 (плотность после двух шагов). Этот график показан зеленым. Как видно, он отличается от оранжевого, и он описывает петлю. Дело в том, что на p1 одна и та же плотность может быть достигнута как при низкой начальной плотности, так и при очень высокой. Петля показывает, что эти два случая тоже немного отличаются по своей эволюции.
Первый десяток и первая сотня
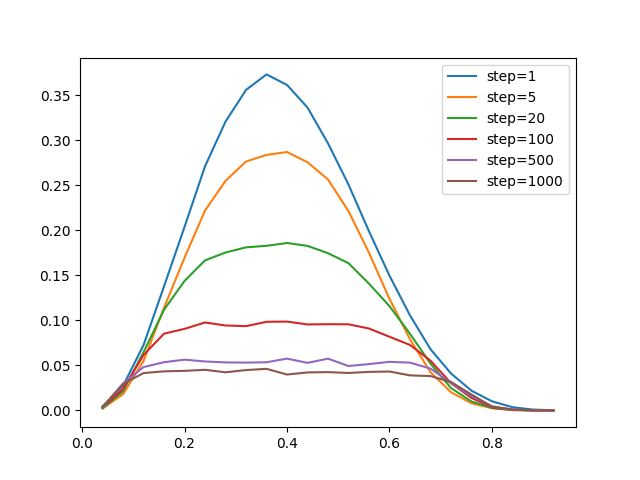
На оси x теперь всегда будем откладывать изначальную плотность, и посмотрим, что происходит в течение десяти шагов:
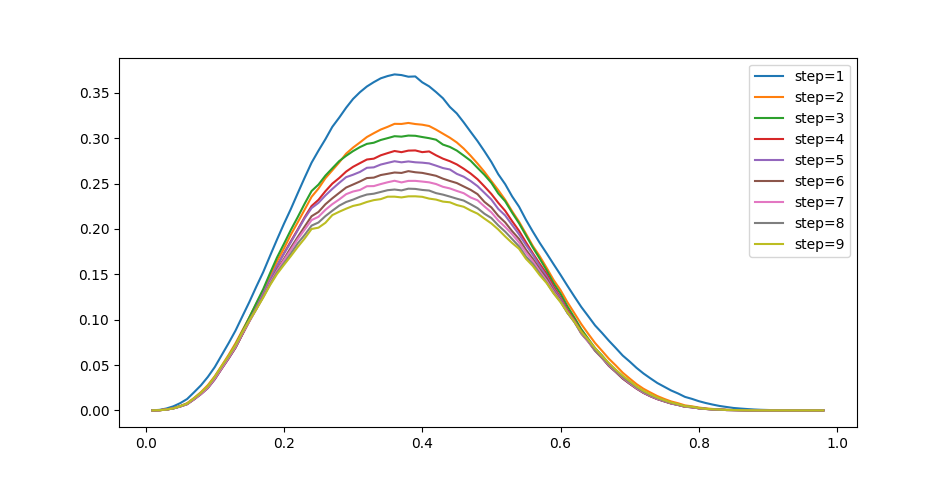
Плотность плавно уменьшается, а максимум сдвигается вправо. Если построить зависимость от времени, то мы увидим интересную вещь:
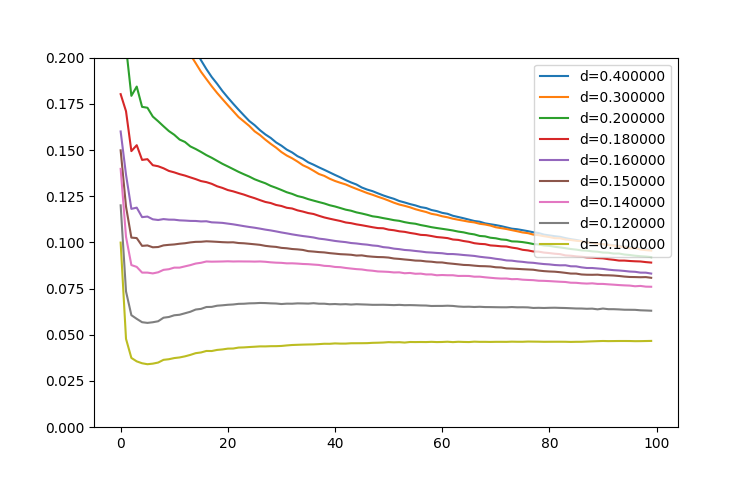
При p<0.15 после первичного и быстрого падения плотности возникает 'ренессанс', плотность после нескольких шагов растет некоторое время. К шагу 100 графики для разных плотностей начинают сближаться. Рассмотрим этот эффект подробнее ниже.
Тысячи шагов
По мере эволюции на графике плотности возникает 'плато':
Обратите внимание, что итоговая плотность после тысячи шагов практически не зависит от изначальной в широком диапазоне p от 0.1 до 0.7. Диаграмма по времени:

Эти линии даже пересекают друг друга. Понаблюдав за игрой глазами, я увидел, что на поле есть куча мертвых статических фигур ('пепел'), типа блоков из четырех клеток и 'ульев', и 'движуха', где всегда что-то происходит, взрывается, контактирует, касается статических конфигураций и оживляет их. Изначальное значение p здесь роли уже не играет.
Однако постепенно 'движуха' ослабевает. Вначале я думал, что это эффект масштаба. Я провел несколько экспериментов с полем разного размера (300, 500, 1000) и зависимости не заметил.
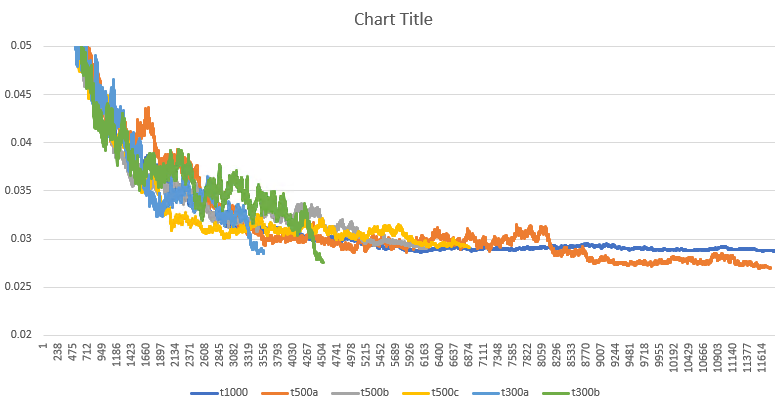
В итоге все заканчивалось 'пеплом' плотности около 0.028 - блоки, мигалки, улья и ряд других статических фигур.
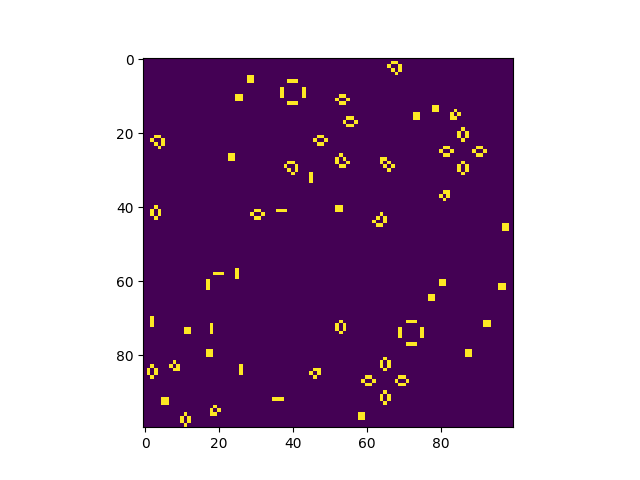
Гугол шагов
Рассмотрим эволюцию при низкой плотности, допустим, p=0.001 Кажется, ничего интересного? Но ведь есть, например, Gosper Glider Gun - ружье, стреляющее глайдерами каждые 14 ходов. Неизвестно, является ли ружье 'садом эдема', но в любом случае оно может получиться чисто случайно. При низкой плотности вероятность появления фигуры из n клеток примерно равна p**n. В ружье 36 клеток, значит вероятность его возникновения в определенном месте равна 1E-102.
UPD: Pavgran меня откорректировал, сообщив что ружье не является садом Эдема:
Не является. Спокойно синтезируется с помощью всего лишь 8 глайдеров.catagolue.hatsya.com/object/yl30_1_5_74055a5f5e513fd2e62fb8d6117d3f03/b3s23
Случайно возникшие ружья будут разделены примерно (1 делить на корень из предыдущего числа) = 1E51 клеткой. Они будут производить глайдер (5) клеток каждые 14 ходов, то есть в среднем 5/14 клетки за ход, постепенно увеличивая плотность, пока сами не будут сжигать друг друга.
Глайдер имеет эффективное сечение 6 клеток, в ружье - ширину 36, то есть зацепить ружье глайдер может на полосе 36+6=6 = 48 клеток. То есть одно ружье убьет другое если попадет в полосу поражения, а на этой полосе одно ружье отстоит от другого на 1E102/48 клеток. Глайдер проходит 1 клетку за 4 хода, то есть он это расстояние пройдет за 1E102/12 шагов. За это время ружье произведет 1E102/12 * 5/14 = 5/168*1E102 клеток, и это в каждом квадрате с ребром 1E51 клетки, то есть в среднем 5/168 = 0.0297 !!! Очень близко к плотности 'пепла'! Совпадение?
Это число на самом деле не зависит от начального p - плотность сокращается, будучи и в числителе, и в знаменателе. Я работал с числами, чтобы показать порядки величин. То есть, через гугол шагов ружья организуют 'движуху', накачав вселенную глайдерами, Если их до этого не сожгут 'реликтовые' глайдеры, получившиеся случайно, и (так как глайдер состоит из всего пяти клеток) в числе куда большем, чем ружья. Зато ружья не двигаются, а реликтовый глайдер наверняка наткнется на фигуру из 4 или 3 клеток, которых еще больше. Итак,
Гипотезы
Первая гипотеза касается окончания 'движухи' - в широком диапазоне изначальных плотностей p от 0.1 до 0.7, после окончания 'движухи' 'пепел' имеет одну и ту же плотность, около 0.27
Так как ружья накачают 'вселенную' глайдерами при сколь угодно малой изначальной плотности, и снова начнется 'движуха', то вторая гипотеза сильнее:
В пределе при любой плотности p (кроме вырожденных случаев p=0, p=1) получается 'пепел' плотности 0.27
Комментарии (52)

forthuser
19.01.2022 17:52+4Стародавняя переведённая книга издательства М.: Мир, 1991.
Тоффоли Т., Марголус Н. Машины клеточных автоматов (рассматривается обобщённо теория клеточных автоматов)
Был и такой проект апаратной симуляции клеточных автоматов
CAM8: a Parallel, Uniform, Scalable Architecture for Cellular Automata Experimentation
P.S. Evolve is an artificial life simulator that I found a few years ago.Evolve 4.0 is a simulator of evolution using a simplified 2-dimensional universe. This software lets you create new simulations, run them, and visualize the behavior of the evolving creatures.

napa3um
19.01.2022 18:05+3Круто. Есть ещё направление исследования, где-то видел статью, насколько различные конфигурации автомата устойчивы к возмущениям. Т.е., берётся какая-то циклично развивающаяся конфигурация, и в неё привносится пятно случайного шума (всё больших и больших размеров), и при эволюции этот шум нивелируется, конфигурация возращается на свой исходный цикл (ну или таки разваливается, уже без восстановления равновесия). Удивило, что вероятность "скушать хаос" не подавившись у конвеевского клеточного автомата довольно высокая :). Не помню конкретных рассуждений, там это как-то через обратимость/необратимость правил анализировали (т.е., для любой конфигурации автомата возможны несколько предыдущих состояний, если пытаться отматывать состояние "в прошлое").

domix32
19.01.2022 18:31+4является ли ружье 'садом эдема'
было бы неплохо пояснять для прочих танкистов, что это такое

Maxim_Q
19.01.2022 18:35-6Какая практическая польза от этого исследования может быть для людей? Я реально не понимаю как это применить на приктике, поясните кто сможет.

balamutang
19.01.2022 18:41+1Ну например из клеточного автомата получается неплохой генератор случайных чисел

Format-X22
20.01.2022 19:47Он же производный получится, можно просто сид игры использовать сразу. Разве что в тайне держать параметры и формулу. Но это тоже по своему сид. Или поясните мне как :)

OlegZH
19.01.2022 19:21+14Вся наша жизнь — езда в незнаемое. Знание чего-то само по себе может считаться значительной силой. Даже, если не ясно, как применить, будет возможность подготовиться к будущему. Например, к такому, где оперативная память будет трёхмерной или, вообще, бутылкой Мёбиуса. Удача любит подготовленных. Более того, за любой вычислительной моделью может стоят красивая метафора. Разве, не красотой будет мир спасён? Хотите понять, как это применить на практике, попробуйте применить к чему-нибудь. Получите глубокие результаты. Дорогу осилит идущий.

napa3um
19.01.2022 19:53+6Клеточный автомат - одна из абстрактных структур "чистой математики", исследование его свойств суть исследование законов нашей вселенной ("предельных моделей возможного") и законов нашего мышления ("предельных моделей мыслимого") :). Пользу можно сформулировать такую же, как от исследований других математических формализмов - расширение инструментария для доказательств теорем :).

phenik
20.01.2022 12:51Клеточный автомат — одна из абстрактных структур «чистой математики», исследование его свойств суть исследование законов нашей вселенной («предельных моделей возможного») и законов нашего мышления («предельных моделей мыслимого») :)
Возможно видели этот комент (под спойлером) — попытка такого самопального исследования)

Maxim_Q
20.01.2022 17:30По минусам я вижу тут не любят людей которые задают вопросы в области которую не понимают и просят помощи.

Milliard
19.01.2022 20:00+1Было бы интересно посчитать процентное соотношение разных конфигураций «пепла» (блоков, мигалок и т. д.) после окончания «движухи».

Pavgran
20.01.2022 13:50+1Для случайных супов размером 16*16 с заполнением 50% собирается огромная статистика здесь:
https://catagolue.hatsya.com/statistics

deepform
19.01.2022 22:46Честно говоря это графики мне очень что-то напоминает связанное с популяциями животных/растений или чем-то уровнем пониже, не помню точно.
Если вспомню - обязательно отпишу

balamutang
20.01.2022 17:40достаточно яркий пример связи клеточных автоматов и животных - это https://ru.wikipedia.org/wiki/Правило_30 расцветка раковины моллюска Conus textile

lightln2
20.01.2022 00:46+4вот тут я вижу как достигают скорости 2.5 миллиона evaluated cells per second на CPU
все-таки там 2.5 миллиарда клеток в секунду, а не миллиона.
А с использованием SSE-команд можно еще быстрее, до 15 миллиардов в секунду: habr.com/ru/post/505606
А в этой статье показывают, что на GPU можно достичь скорости, если я не ошибся в подсчетах, полтора триллиона клеток в секунду!
iShrimp
20.01.2022 18:38Вроде, на больших игровых полях преимущество у алгоритма HashLife (он просто хеширует и воспроизводит уже известные паттерны).

liddom
20.01.2022 04:10Кстати интересно, какова вероятность зацикливания "жизни" за определенное количество шагов в зависимости от размерности поля и плотности заселения?
Существует ли такая конфигурация, которая бы эволюционировала бесконечно на конечном количестве клеток? Это же наверно доказывается математически.
Беглое гугление ответов на эти вопросы не дало.

liddom
20.01.2022 04:22+3Очевидно, что при конечном количестве клеток бесконечная эволюция означает, что рано или поздно любая возможная конфигурация клеток будет достигнута. Также очевидно, что есть такие конфигурации, которые зацикливаются. Т.е. очевидно, что бесконечная эволюция невозможна. Максимум на что можно рассчитывать это зацикливание с достаточно длинным циклом. Тогда вопрос такой: какова теоретическая максимальная длина цикла для поля с заданным количеством клеток.

ciubotaru
20.01.2022 08:45+3рано или поздно любая возможная конфигурация клеток будет достигнута.
Клеточный автомат можно представить как ориентированный граф состояний (или, как Вы говорите, конфигураций), со следующими свойствами:
из каждой вершины исходит ровно одно ребро;
в каждую вершину входит от нуля до n ребер (прим.: если входящих рёбер нет, то это т.н. "райский сад" -- "начало" графа);
граф слабо связанный и может состоять из нескольких отдельных под-графов;
исходящее ребро может возвращаться в ту же вершину (прим.: т.е. правила клеточного автомата возвращают исходное состояние.-- например пустое поле навсегда останется пустым -- "конец" графа);
Таким образом, практически для любого исходного состояния существуют такие целевые состояния, которые невозможно достичь ни за какое число итераций.
Тогда вопрос такой: какова теоретическая максимальная длина цикла для поля с заданным количеством клеток.
Поскольку граф может быть (и, чаще всего, будет) несвязанным и соответственно циклов может быть больше одного, на Ваш вопрос очень сложно дать ответ.

Tyusha
20.01.2022 11:48+2Очевидно, что при конечном количестве клеток бесконечная эволюция означает, что рано или поздно любая возможная конфигурация клеток будет достигнута.
Нет. С чего вдруг? Бесконечная эволюция конечной системы означает лишь то, что какие-то (но не обязательно все) конфигурации будут повторяться.

liddom
20.01.2022 11:50Для детерминированного клеточного автомата факт того, что какие-то конфигурации повторяются означает, что автомат попал в цикл, что в моем понимании означает окончание "эволюции".

Tzimie Автор
20.01.2022 13:13в игре жизнь можно создать машину тьюринга и заставить ее бесконечно прибалять единицы. Является ли это бесконечным циклом? Ведь ее состояние (текущее число) каждый раз разное

dmitrysvd
20.01.2022 13:19+1Если у поля есть граница, или она завернута в тор, то она уже не соответствует машине Тьюринга, так как у МТ должна быть бесконечная память

NickKolok
20.01.2022 04:36+1Если я правильно понял второй вопрос, то не существует. Пусть клеток N, тогда возможных конфигураций 2^N, а никак не бесконечность.

amarao
20.01.2022 13:07если эволюция - это создание новых конфигураций (которых не было раньше), то это не возможно. game of life конечный автомат, а любой конечный автомат обязательно зацикливается (либо на нетривиальном цикле, либо на каком-то одном состоянии, включая halt).
если эволюция - это "мигание на экране" (т.е. следующий кадр отличается от предыдущего), то да, такие конфигурации есть и они тривиальны.


Tzimie Автор
20.01.2022 13:14в игре жизнь можно создать машину тьюринга и заставить ее бесконечно прибалять единицы. состояния клеток не повторяются

amarao
20.01.2022 13:29Вы не можете создать машину Тьюринга (цитата из комментария, на который я отвечаю) на конечном количестве клеток.
Машина Тьюринга требует бесконечной ленты, а вы не можете уместить бесконечную ленту в конечное хранилище.

iShrimp
20.01.2022 18:56+2На бесконечном поле есть такой интересный класс конфигураций, как паровозы. Они движутся со скоростью с/2 и оставляют за собой псевдослучайный мусор, период которого растёт экспоненциально с увеличением ширины паровоза (гуглить Line puffer). Прикол в том, что некоторые конфигурации могут быть нестабильными, и срок их жизни может оказаться очень большим - в десятки миллионов поколений - но конечным. Однажды в выхлопе может сформироваться такой набор клеток, который разрушает "паровоз".

Miiko
20.01.2022 07:18+5Из работы https://hal.archives-ouvertes.fr/hal-02399681/document
It appears in simulations [21, 27, 24, 16] that there is an interval 0.15 < ρin < 0.75 for which the density ρ∗ of the final quiescent state is constant within the accuracy of the simulation
ρ∗ = 0.02872 ± 0.00001
Достаточно близко к Вашей первой гипотезе (с учетом исправленной опечатки)

Tzimie Автор
20.01.2022 13:20мне показалось очень интересной диаграмма в начале пятой страницы. То есть при L->inf, при бесканечном поле, время окончания движухи конечно и около (если продлить прямую) около 100K
P.S. Странно что они на таких маленьких матрицах пробовали, это все таки 2018 год...

Chumachechy
20.01.2022 10:32Любопытно, спасибо!
Раз уж это назвали "жизнь", следующим шагом м.б. наложение на равномерную среду (сейчас) медлено изменяющегося, по пространству, градиента- множителя к вероятности. Т.е. эмулировать в одних областях "угнетение"-понижение вероятности (неблагоприятная среда) и "поддержка" - повышение вероятности (благоприятная среда).

Tyusha
20.01.2022 11:51Слишком самонадеянные выводы. Вы знаете только одно ружьё. Но где гарантии, что нет других неизвестных пока ружей или же наоборот пожирателей.

Tzimie Автор
20.01.2022 13:15+2есть и другие ружья. Я согласен, что эта тема еще ждет своих исследователей. Меня больше беспокоят не другие ружья, а выживаемость ружей при наличии 'реликтового' излучения глайдеров
leshabirukov
20.01.2022 16:19+1Реликтовое излучение со временем сходит на нет, зародыш роста порядка можно защитить коконом из разреженных блоков на время горячего старта вселенной. Правда потом ему всё равно понадобится кожа, способная поглощать шальные глайдеры, да еще и расти, расчищая пепел по дороге.

akomiagin
20.01.2022 13:59+1Уже не новая, но очень совеременная и актуальная тема! Сейчас очень активно используется в моделировании онкологических изменений. Например, интересное исследование https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6377620/

etoropov
20.01.2022 17:43Интересно
Сколько раз вы запускали? По отсутствию погрешностей я понял что запускалось только один раз, и плотность 0.028 это в конце только одной симуляции?
Если запускалось много раз, то хочется гистограмму плотности пепла по симуляциям.
Графики честно трудно понимать, оси как-то странно подписаны.
Предлагаю "пепел" считать реликтовым излучением. Тогда хочется график со спектром реликтового излучения (распеределению его плотности) :)
Можно устроить биг бэн с последующим инфляционным расширением вселенной :/ Например на каждом шаге после каждой N-ой строки и N-ого столбца вставляется еще одна строка и столбец, а состояние каждой вставленной клетки определяется состоянием ее соседей

balamutang
20.01.2022 17:50Можно устроить биг бэн с последующим инфляционным расширением вселенной :/ Например на каждом шаге после каждой N-ой строки и N-ого столбца вставляется еще одна строка и столбец, а состояние каждой вставленной клетки определяется состоянием ее соседей
Эээ, да вам к Стивену Вольфраму надо :)

TimeCoder
22.01.2022 09:43У игры вообще нет устойчивых стартовых условий? В любом случае со временем мир вырождается в "пепел", где по кругу идут слабые флуктуации?

Tzimie Автор
22.01.2022 10:06Есть конечно, то же ружье. Просто оно должно быть в пустоте. Или машина Тьюринга

TimeCoder
22.01.2022 10:54Ружьё будет постоянно выстреливать глайдеры, поэтому клетки не выродятся, но будет ли в том мире какое-то развитие? В смысле, что даже через миллиард поколений появляются какие-то новые фигуры, которых ранее не было.



amarao
Точная плотность пепла на бесконечности - 0.023809523809523808.
1/42
stranger169
(ответ на главный вопрос жизни, вселенной и всего такого)^(-1)
ToRcH2565
Но каков же вопрос?
stranger169
В какой-то из книг Дугласа Адамса вроде было. Почитайте )