
Как вы думаете, существует ли треугольник с углами 41, 76 и 63 градусов?
Поначалу кажется, что ответ прост. Из уроков геометрии мы знаем, что сумма внутренних углов треугольника равна 180 градусам, и поскольку 41 + 76 + 63 = 180, ответом будет «да».
Но в этом вопросе есть и невидимая поначалу сторона. Теорема о сумме углов треугольника гласит, что для треугольника в плоской евклидовой геометрии сумма внутренних углов равна 180 градусов. Но в нашей задаче не даётся треугольник, а спрашивается, существует ли он. Теорема о сумме углов треугольника не отвечает непосредственно на этот вопрос, однако помогает построить нужный нам треугольник.
Чтобы соответствовать требованиям теоремы о сумме углов треугольника, каждый угол треугольника должен быть меньше 180 градусов, то есть мы всегда можем разместить два из них на одной стороне отрезка прямой. Давайте поместим угол в 41 градусов и угол в 76 градусов на одной из сторон отрезка прямой AB:

Исходящие из A и B лучи не могут быть параллельными, потому что в евклидовой геометрии такие углы, «внутренние для одной стороны», должны быть «смежными», то есть в сумме давать 180 градусов. Но эти углы не имеют такой суммы, то есть лучи не параллельны, а поскольку они не параллельны, они должны пересекаться.
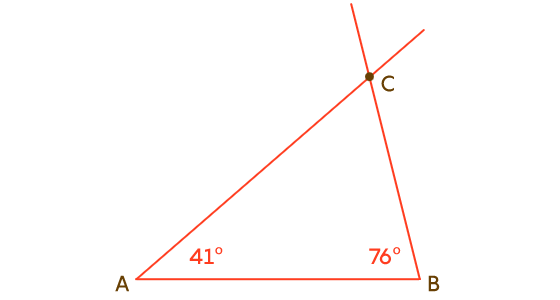
Обозначим их пересечение как C. Теперь у нас есть треугольник и мы можем применить теорему о сумме углов треугольника. Третий угол должен иметь величину 180 − (41 + 76) = 63, поэтому
Это рассуждением можно обобщить, чтобы показать, что любые три величины угла, в сумме дающие 180 градусов, могут составить треугольник, и из этого непосредственно следует, что можно легко найти треугольники, все величины углов которых (в градусах) являются рациональными числами. Давайте начнём с двух положительных рациональных чисел, сумма которых меньше 180; назовём их x и y. Тогда 180 − (x + y) тоже является рациональным числом, а поскольку x + y + (180 − (x + y)) = 180, мы можем составить треугольник с этими тремя рациональными углами.
Несмотря на простоту создания треугольников с рациональными углами, похожая задача в трёх измерениях оказалась настолько сложной, что для её решения лучшим математикам мира потребовались десятки лет. Почему при увеличении размерности на одну эта задача становится настолько сложнее? Поняв это, мы станем ещё больше ценить теорему о сумме углов треугольника.
В схожей задаче в трёх измерениях задействованы тетраэдры — четырёхсторонние фигуры с треугольными гранями. Можно считать их трёхмерными версиями треугольников. В двух измерениях треугольник является простейшей замкнутой фигурой, которую можно составить из плоских сторон, и для этого требуется три отрезка прямых. В трёх измерениях тетраэдр — простейшая замкнутая фигура, которую можно составить из плоских сторон, и для этого требуется четыре треугольных грани.

Четыре треугольных грани тетраэдра схожи с тремя сторонами треугольника. Но как нам воспринимать углы? Можно представить «сплошной угол» на каждой из четырёх вершин тетраэдра. Но в интересующем нас вопросе задействуются «двугранные углы», образуемые пересекающимися гранями.
Если начертить две пересекающиеся плоскости, обнаружится множество разных углов, которые можно измерить. Какой из них выбрать, для задания двугранного угла?
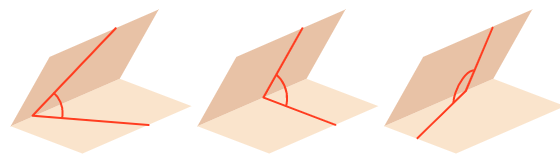
Ответ заключается в том, чтобы поворачивать пересекающиеся грани, пока они не будут похожи на двухмерный угол.
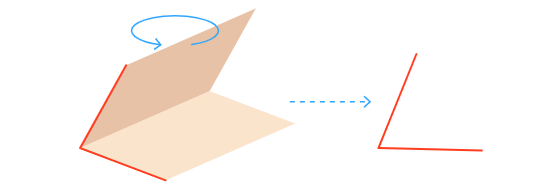
Именно этот угол мы ассоциируем с двугранным углом.
В тетраэдре каждая из четырёх граней пересекается со всеми остальными гранями, образуя шесть рёбер и шесть двугранных углов. Десятилетиями математики задавались вопросом, какие тетраэдры имеют шесть рациональных двугранных углов. Как и говорилось ранее, угол считается рациональным, если его угловая мера является рациональным числом. Это эквивалент того, что его мера в радианах является рациональным числом, кратным
Мы уже знаем, насколько легко составлять треугольники с рациональными углами, но в случае тетраэдров задача гораздо сложнее. Рассмотрим следующий простой тетраэдр
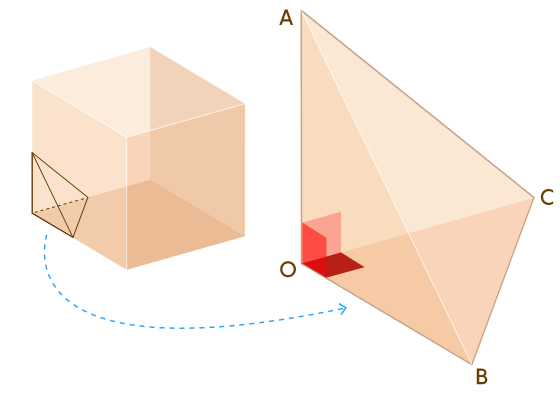
Мы сразу же видим, что три двугранных угла в этом тетраэдре являются прямыми, поскольку они образованы гранями куба. Удобно обозначить каждый двугранный угол по его ребру, так что в этом тетраэдре двугранные углы при
Если мы срежем куб так, что

Если повернуть тетраэдр так, чтобы смотреть на двугранный угол при
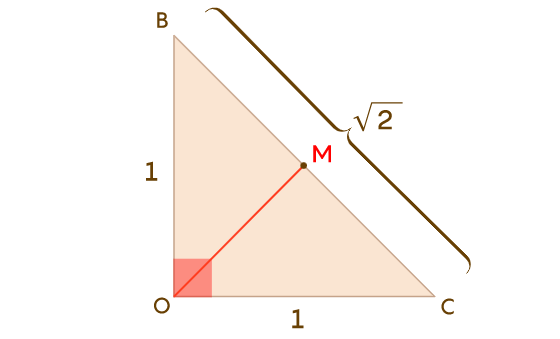
Так как
Теперь мы наконец готовы найти величину
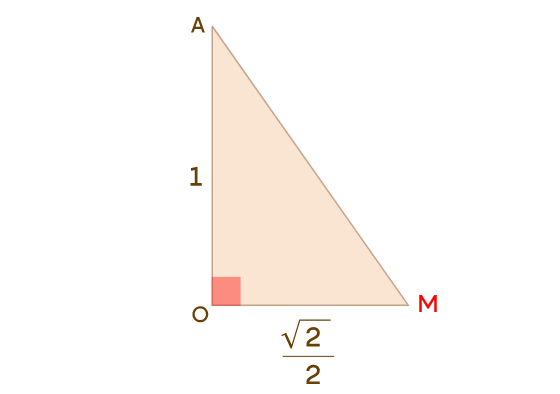
В
То есть величиной
Чтобы понять это, давайте найдём приблизительную сумму двугранных углов в нашем иррациональном тетраэдре. При помощи калькулятора или тригонометрической таблицы мы выясним, что приблизительная величина
Теперь мы можем суммировать шесть двугранных углов тетраэдра
И здесь дело принимает неожиданный поворот. Давайте вернёмся к кубу и вместо того, чтобы срезать его так, что
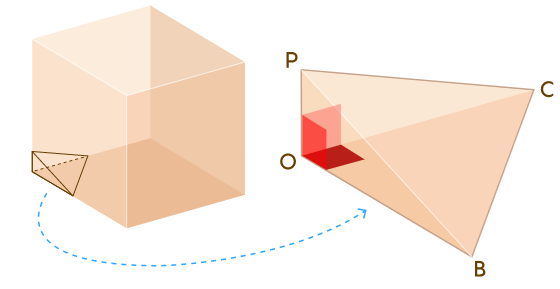
Этот новый тетраэдр тоже будет иметь три 90-градусных двугранных угла при
На самом деле, если продолжать делать всё более тонкие срезы,
При приближении
Оказывается, в лучшем случае мы можем гарантировать, что сумма шести двугранных углов тетраэдра находится в интервале от 360 до 540 градусов. А если вы ищете тетраэдры с рациональными двугранными углами, это становится проблемой. Нельзя просто выбрать пять рациональных углов и быть уверенным, что шестой автоматически будет рациональным, потому что, в отличие от случая с треугольником, мы понятия не имеем, какой должна быть сумма.
Хуже того, мы даже не можем быть уверенными, что любые шесть углов могут быть двугранными углами тетраэдра. Рассмотрим пять прямых углов и один острый. Сумма этих шести углов находится в интервале от 450 до 540 градусов, что лежит в рамках приемлемого для тетраэдра интервала. Но тетраэдра с такими шестью величинами углов не существует. Если пять из шести двугранных углов являются прямыми, то одна из граней должна иметь три прямых двугранных угла. Но если это так, то такие грани не замыкаются и не образуют тетраэдр: как параллельные линии они никогда не пересекаются.

Грани, пересекающиеся в трёх прямых двугранных углах, могут быть частью пятигранной призмы, но не тетраэдра.
Следовательно, для решения задачи поиска всех возможных рациональных тетраэдров требуется больше, чем просто найти пять или шесть рациональных чисел с определённой суммой. Среди прочего, для этого требуется решить уравнение с 105 членами, источником которого стала статья 1976 года, написанная Джоном Конвеем и Антонией Джонс. Группа математиков справилась с этой задачей в 2020 году, и результатом стала полная классификация всех рациональных тетраэдров.
Теорема о сумме углов треугольников — одна из множества причин восхищаться красотой и изяществом треугольников. Отсутствие такой теоремы для тетраэдров — причина для того, чтобы ценить их красоту и сложность в пространстве на одно измерение больше.
Упражнения
1. Какова сумма двугранных углов в кубе?
2. Какова (приблизительная) сумма шести двугранных углов в правильном тетраэдре?
3. Представьте правильный тетраэдр, стоящий на столе. Если опускать верхнюю вершину к нижней грани, как будет меняться сумма шести двугранных углов?
4. Могут ли какие-нибудь четыре угла с суммой 360 градусов быть углами четырёхугольника?
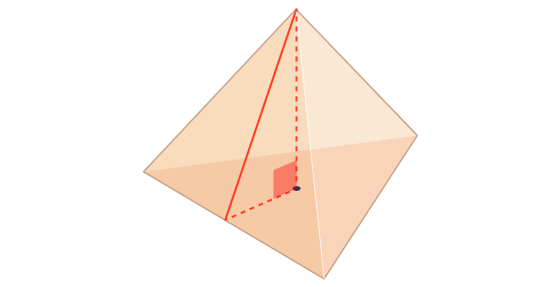
Все грани правильного тетраэдра являются равносторонними треугольниками, поэтому медиана (отрезок от вершины до средней точки) грани имеет длину
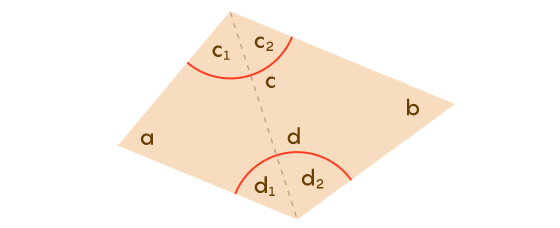
Интересная задача: разобраться, можно ли всегда составить четырёхугольник с углами в определённом порядке.
Комментарии (12)

amarao
21.02.2022 12:05+3Меня тоже не покидал вопрос о смысле. Для чего длину сторон хочется иметь рациональной - понятно. Приятно строить. А углы? Их же всё равно строят с помощью сторон.
Или, с практической точки зрения, что в каком процессе становится проще, если углы рациональные?

iShrimp
21.02.2022 17:37+1Да и вообще, что такое «рациональный угол»?
Например, 180° — это π радиан, иррациональное число. А 1 радиан - рациональное. Все тригонометрические функции вычисляются от аргумента в радианах, а градусы были введены людьми искусственно.

vanxant
21.02.2022 19:33+2радианы, в общем тоже искусственны. Естественным является полный оборот, он же 360 градусов. Ну да, разложение синусов в ряд пришлось бы подпилить, но сколько головной боли от «круговых частот» бы ушло…

Naf2000
21.02.2022 12:32+4Если все же оперировать телесными углами в вершинах тетраэдра, то очевидно, что их сумма постоянна и равна 4*pi/3 стерадиан

runaway
21.02.2022 18:13Аналогом плоского угла в стереометрии является телесный угол. Так что тут какая-то странная попытка использовать некорректный инструмент. Это как пытаться описывать алгебру комплексных чисел, используя только действительные, и при любой нестыковке кричать - Ага! Не сходится!

Alexandroppolus
21.02.2022 19:02С тетраэдрами есть ещё интересный вопрос: при каких размерностях N можно расположить правильный N-мерный тетраэдр так, что все вершины (коих N+1 штук) будут с целочисленными координатами? Легко сделать это для N = m^2 - 1, и легко доказать, что для всех четных N, не равных m^2 - 1 так сделать нельзя (из-за иррационального объема), а вот про остальные непонятно..

omxela
21.02.2022 22:27При чтении я вдруг подумал: а почему, собственно, тетраэдр - это трехмерный аналог треугольника? Потому, что грани треугольные? Это, конечно, аргумент. Но если я хочу вывести плоский треугольник в 3D, я возьму и потащу его в этом самом третьем измерении. И получу упомянутую в тексте пятигранную призму. С её углами всё в порядке.

samsergey
21.02.2022 22:47Треугольник, тетраэдр, пятиячейник и так далее -- это симплексы, простейшие выпуклые оболочки для минимальных множеств афинно независимых точек в афинном пространстве.
Логика тут такая. Точку можно сдвинуть вдоль вектора и получить отрезок. Любую точку отрезка можно вывести из полученного подпространства, "подняв" в каком-либо ином направлении. Далее любую точку треугольника можно вытащить в новое "измерение", получив пирамиду.
Процесс, описанный вами порождает иную последовательность фигур: точка -> отрезок -> параллелограмм -> косой параллелепипед (призма) -> 4-мерный гиперкуб т. д. Это тоже полезные политопы, но они не являются минимальными (симплектическими).

DaneSoul
22.02.2022 00:144. Могут ли какие-нибудь четыре угла с суммой 360 градусов быть углами четырёхугольника?
В условии не сказано, что углы не могут быть все равны.
360/4 = 90, то есть квадрат, который тоже является четырехугольником.
Поэтому ознозначно МОГУТ.


Foxbator
А есть какой-нибудь практический смысл в нахождении тетраэдров именно с рациональными углами? В статье рассмотрены именно углы между гранями, а существуют ли треугольники со всеми рациональными углами? В том числе с рациональным углами граней?
Manyak872
Нет, потому что Солнце не вечно, а там и тепловая смерть Вселенной…
Да, (додумав, что имеются в виду треугольники, являющиеся гранями тетраэдра) — правильный тетраэдр же.
Хороший вопрос. Чтобы ответить, нужно бы перебрать те 59 полученных тетраэдров.