28.04.2022 00:31
petuhoff 6 1700 Источник

Стандарт цифровых двойников определяет цифровую модель изделия как “систему верифицированных и валидированных математических, компьютерных моделей и электронных документов изделия, описывающих поведение вновь разрабатываемого или эксплуатируемого изделия на различных стадиях жизненного цикла, использующую программные средства импорта и экспорта моделей и электронных документов, программные средства численного решения задач и компьютерного моделирования, а также визуализации”.

Другими словами, цифровой двойник — это не одна модель, а система моделей или набор моделей, каждая из которых предназначена для решения конкретных задач в рамках жизненного цикла изделия. Требования к конкретной модели определяются задачами, решаемыми с помощью данной модели.

В статье описан реальный опыт создания модели системы электроснабжения самолета (СЭС) в рамках реализации методов модельно-ориентированного проектирования в авиации.

Введение

Очевидно, что для разных систем создаются разные модели (например, комплексная модель самолета: электрическая система, топливная система, система управления). Каждая из которых может быть описана разными физическими и математическими уравнениями. Часть систем, например, топливная и система кондиционирования, описываются одинаковыми физическими уравнениями (модель течения и теплообмена среды в трубах). В этом случае можно использовать одинаковые уравнения физики и одинаковые приближения. Часть систем реального объекта всегда взаимосвязана, очень часто один узел является частью двух систем. Например, в авиационных системах используют теплообменник «топлив-воздух», где с одной стороны – топливо из топливной системы, а с другой – воздух системы кондиционирования. Видеопример здесь:

Также нередкой является ситуация, когда одну и ту же физическую систему мы моделируем, используя разные математические модели, в зависимости задач, решаемых моделью.  В статье "Модельно ориентированное проектирование. Создание достоверной модели, на примере авиационного теплообменника": рассказано, как создавать модель, предназначенную для отладки системы управления на примере теплообменника системы кондиционирования воздуха самолета, какая точность нам нужна и как можно ее обеспечить. В примере теплообменника мы могли настроить модель по результатам испытаний реального аппарата, который уже создан и доступен для испытаний на стенде. Но если мы находимся на стадии проектирования, то мы вынуждены создавать предварительную, но достаточно достоверную математическую модель еще не существующего объекта.

В основе такой предварительной модели, как правило, лежит набор (библиотека) моделей для компонентов и (или) агрегатов проектируемой системы, которые обеспечивают расчет требуемых параметров системы с необходимой точностью. Создание такой библиотеки моделей компонентов является отдельной задачей, поскольку выбор принимаемых в модели допущений и упрощений диктуется требованиями к результату расчета, меняющимися в зависимости от стадии жизненного цикла процесса проектирования и изготовления.

Жизненный цикл в модельно-ориентированном подходе

Рассмотрим пример модельно-ориентированного подхода к проектированию на примере системы электроснабжения самолета (СЭС). Обобщенный жизненный цикл модели и проекта можно представить виде диаграммы на рисунке 1. Данную диаграмму можно применить к любой сложной технической системе. Применим ее к системе электроснабжения.

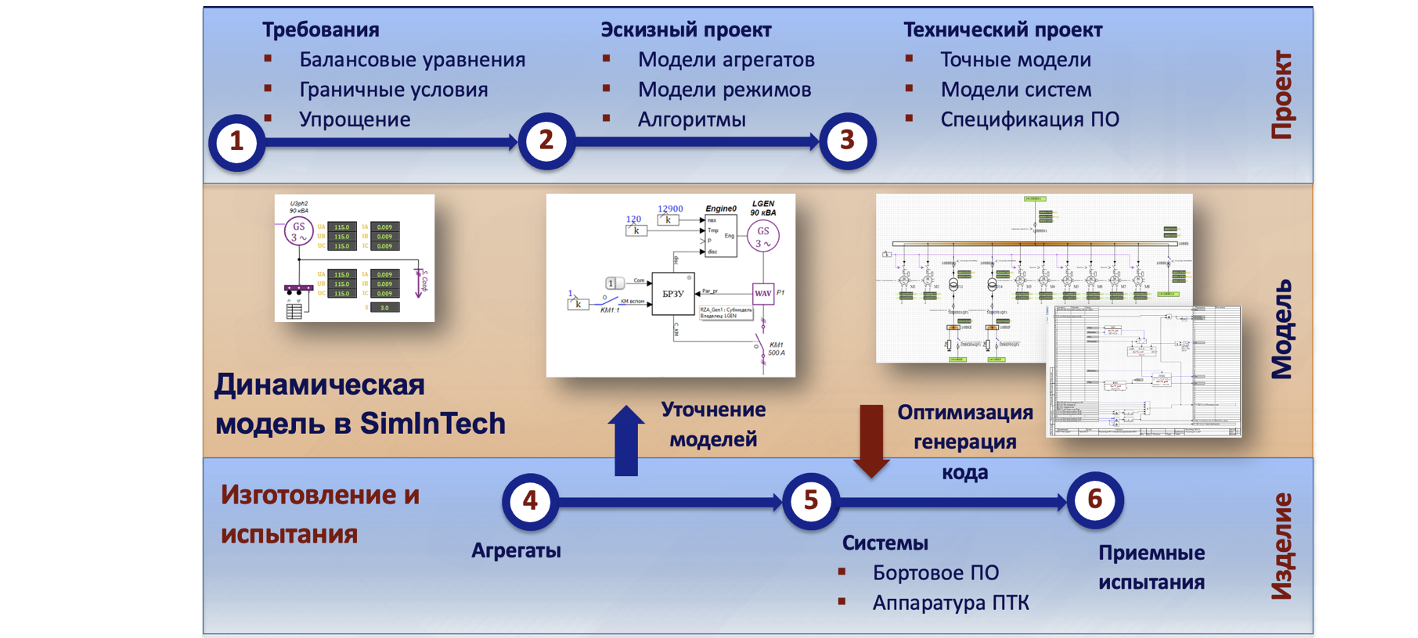
Рисунок 1. Жизненный цикл модели в модельно-ориентированном подходе.
Рисунок 1. Жизненный цикл модели в модельно-ориентированном подходе.

Первая стадия создания модели обеспечивает выбор основных решений и номинальных параметров электрической схемы. Для авиационной СЭС это может быть выбор двухканальной системы или четырехканальной системы, количество и необходимая мощность генераторов, схема переключения и изменения нагрузки в полете. Нагрузка в этом случае задается как граничные условия из требований проекта. Модель первой стадии позволяет оценить варианты и начать эскизный проект.

На стадии эскизного проекта в модели определяются режимы работы и основные алгоритмы управления системой, в том числе алгоритмы защиты. Здесь проверяются работоспособность выбранной принципиальной электрической схемы в динамических режимах работы. При этом уточняется нагрузка со стороны потребителей электроэнергии, а также динамика работы основных источников механической энергии в генераторах.

Точный технический проект позволяет создать полную и максимально точную модель работы электрических систем в мгновенных значениях тока и напряжения. При этом данная модель позволяет исследовать электромеханические взаимодействия в комплексной модели совместно с моделями топливной системы, системы вентиляции, системы связи и другими системами самолета. 

По мере изготовления агрегатов модели уточняются по результатам стендовых испытаний, что позволяет добиться полного совпадения поведения реальных систем и моделей с точностью, достаточной для отладки и оптимизации алгоритмов управления в режиме совместного моделирования. Данный подход позволяет создать цифровой полигон для сокращения цикла реальных испытаний.

Обобщенная диаграмма жизненного цикла модели (рис. 1) позволяет выделить три уровня моделирования систем электроснабжения самолета, которые фактически и были реализованы в данном проекте.

Три уровня модели системы энергоснабжения самолета

  1. Модель первого уровня применяется для выбора архитектуры СЭС или сравнения различных архитектур, определения необходимого бюджета мощности СЭС, анализа электрических нагрузок, предварительного определения номиналов аппаратов защиты, исходя из принципа селективности. Модель не учитывает изменения токов и напряжений относительно номиналов.

  2. Модель второго уровня применяется для отработки логических законов или алгоритмов переключения шин СЭС, необходимых для реализации реакции СЭС на управляющие воздействия и реконфигурации СЭС в случае отказов. Модель также применяется для окончательного определения номиналов аппаратов защиты, исходя из принципа селективности. Модель учитывает изменения токов и напряжений во временном масштабе, оперируя действующими значениями токов и напряжений в подсистеме электроснабжения переменного тока и средними значениями напряжений и токов в подсистеме электроснабжения постоянного тока.

  3. Модель третьего уровня применяется для комплексного анализа переходных процессов во времени. Обеспечивает отдельный расчет токов и напряжений в каждой фазе ЭС с возможностью расчёта несимметричных по фазам нагрузок, и учета нелинейности в электрических и магнитных цепях. Для расчета используются мгновенные значениях тока и напряжения в системе.

Данные уровни моделирования совпадают со стадиями проектирования при использовании модельно-ориентированного подхода (см. рис. 1) 

Важное замечание. Если задачи, решаемые в процессе проектирования, могут быть решены первым уровнем модели, то использование второго и третьего уровня не является обязательным и целесообразным. Например, можно проводить анализ различной конфигурации системы для выбора количества генераторов, их мощности и схемы подключения в зависимости от режимов электрических нагрузок во время полета. И создание модели второго уровня будет излишним.

Для иллюстрации возрастания сложности рассмотрим, как выглядит модель первого и второго уровней на примере авиационного электрического генератора. 

Модель 1-го уровня.

Модель синхронного генератора уровня 1 основана на схеме замещения, представленной на рисунке 2. Исходные данные для расчета параметров схемы замещения задаются в свойствах элемента, приведенных в таблице 1. Принимается, что ЭДС и внутренние сопротивления симметричны.

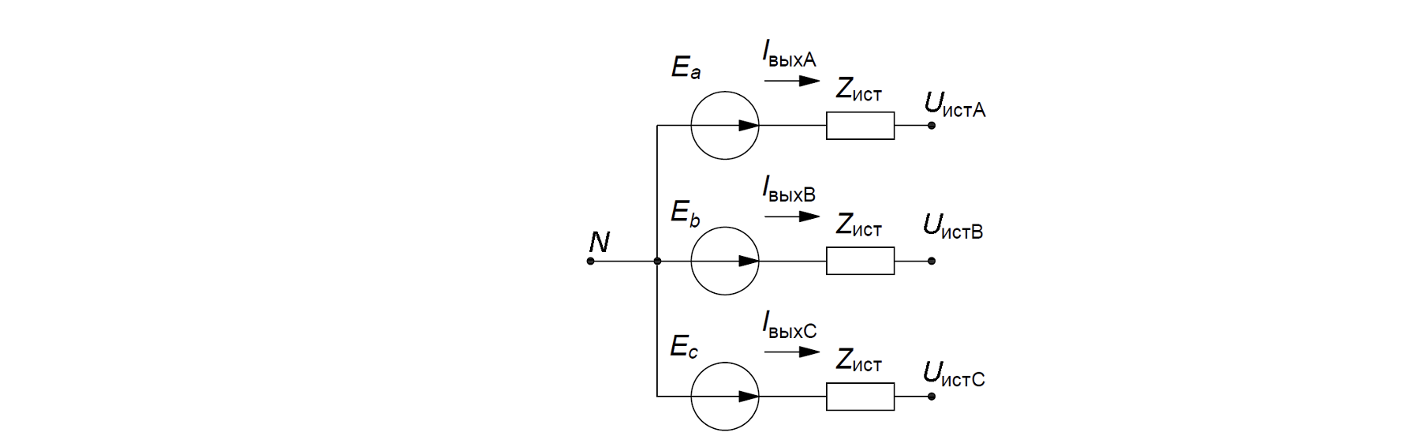
Рисунок 2. Схема замещения трёхфазного синхронного генератора модели уровня 1
Рисунок 2. Схема замещения трёхфазного синхронного генератора модели уровня 1

 где: E_A, E_B,E_C- ЭДС фаз генератора;  I_{выхA}, I_{выхB},I_{выхС}– токи фаз генератора, определяемые при расчете;  Z_G– полное сопротивление синхронного генератора; N – вывод нейтрали

Схеме замещения соответствует выражение (для каждой из фаз):

\dot{U}_{G.Ф}=\dot{E}_Ф- \dot{I}_{вых.Ф}\cdot Z_G = (E_{Ф.re}+j \cdot E_{Ф.im})-\dot{I}\cdot R

где: \dot{E}_Ф=U \angle \phi; \ \ E_{Ф.re},E_{Ф.im}– действительные и мнимые составляющие ЭДС фаз генератора.

Таблица 1 – Исходные данные для расчета параметров схемы замещения синхронного генератора модели уровня 1.

Наименование свойства

Обозначение

Напряжение (фазное), В

U

Угол фазы А, эл.гр.

φ

Частота, Гц

f

Номинальная мощность, Вт

Snom

Коэффициент мощности, о.е.

cosφ

Вид цепи сопротивления источника

R (нет)

Характер внутреннего сопротивления синхронного генератора изменяется в зависимости от значения свойства «Вид цепи сопротивления генератора» («R», «нет»). При значении «нет» Z_{ист}=0 и напряжение каждой фазы равно соответствующей ЭДС.

При значении свойства элемента «Задать напряжение через порт» равному «Да» у элемента появляются управляющий порт «U» и ЭДС фаз определяется управляющим сигналом – действующее значение напряжения. При значении «Нет» ЭДС определяются свойствами элемента. В обоих случаях ЭДС описываются выражениями:

\dot{E}_A=U\angle\phi, \\\dot{E}_B=\alpha^2U\angle \phi,\\ \dot{E_c}=\alpha U\angle\phi.

где оператор \alpha = 1\angle120^o.

Для моделирования готовности (отказа) генератора предусмотрен сигнал, который подаётся с помощью блока «в память» по локальному имени блока синхронного генератора модели уровня 1. Переменная в блоке «в память» задается в формате «имя генератора_rdy». Например: «L_GEN_rdy». При отсутствии сигнала в блок «в память» считается, что генератор готов к работе.

Для данного блока можно использовать функцию сигнализации.  Сигнализация срабатывает по мощности. Для этого в свойствах модели необходимо задать свойство «Уставки сигнализации по перегрузке [S_p, S_av], о.е.» и время срабатывания сигнализации. Сигнализация имеет две ступени: предупредительная уставка и аварийная уставка. Предупредительной уставке соответствует первый элемент вектора, а аварийной – последний. Функции сигнализации и отображения величин выполняются посредством элемента «ЭСЛА-Датчик», который дополнительно может устанавливаться на расчетную схему.

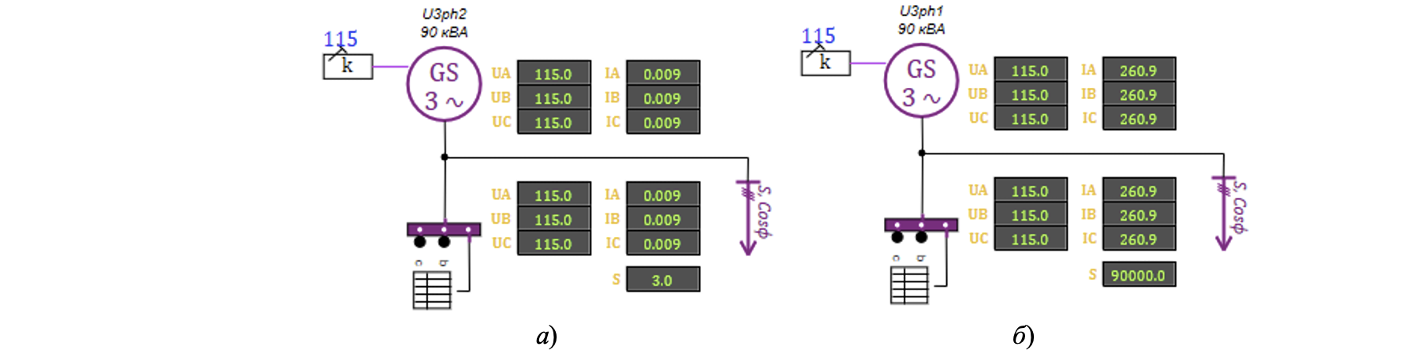
В процессе расчета данная модель обеспечивает отображение нагрузки для генератора в процессе расчета режимов полета. На рисунке 2: отображение процесса моделирования для двух вариантов нагрузок:

Рисунок 3. – Скриншот испытаний синхронного генератора: а) трехфазная нагрузка 3 ВА; б) трехфазная нагрузка 90 кВА.
Рисунок 3. – Скриншот испытаний синхронного генератора: а) трехфазная нагрузка 3 ВА; б) трехфазная нагрузка 90 кВА.

Общая схема электроснабжения самолета модели первого уровня выглядит, как показано на рисунке  3.

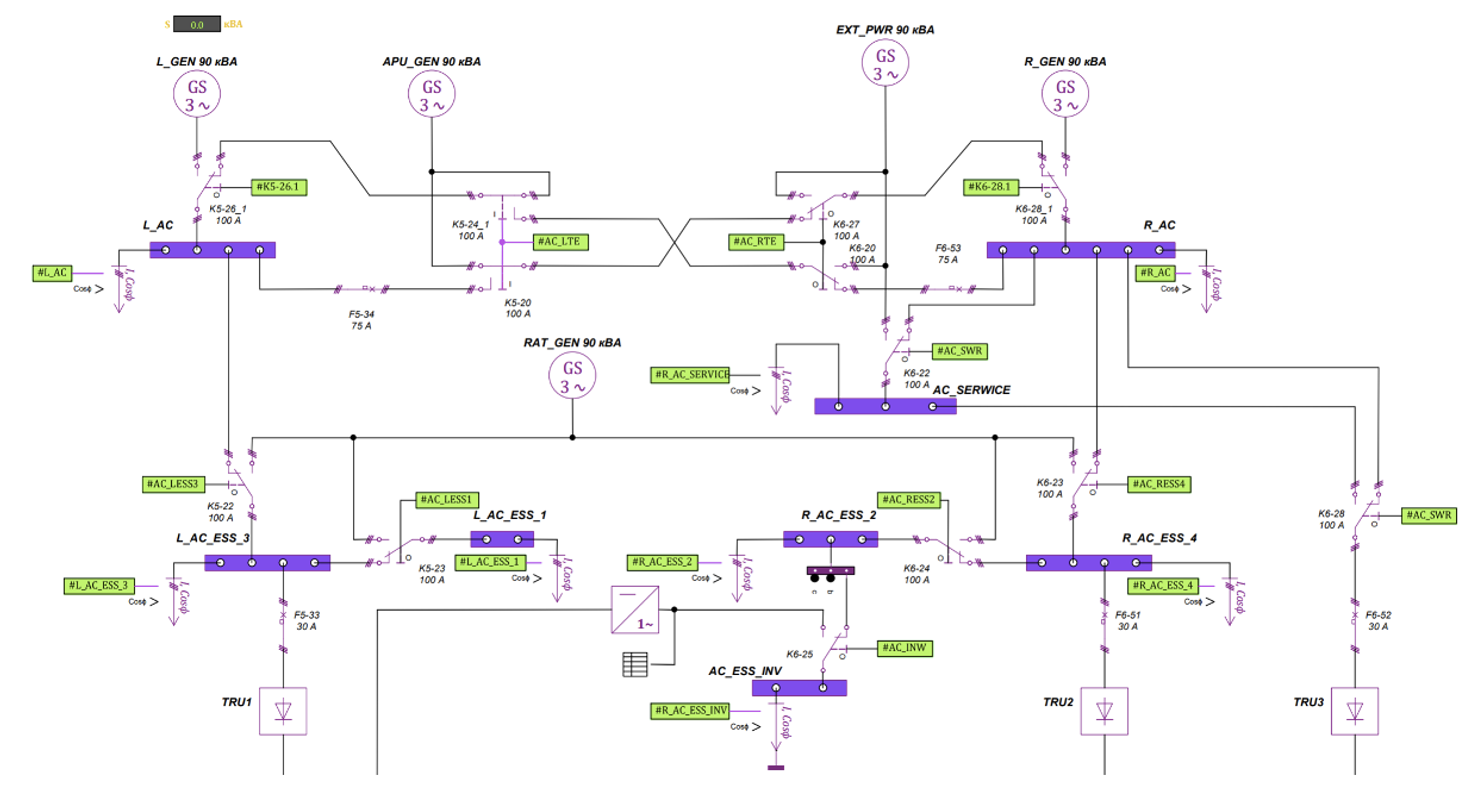
Рисунок 4 – Пример схемы СЭС модели первого уровня: сегмент переменного тока.
Рисунок 4 – Пример схемы СЭС модели первого уровня: сегмент переменного тока.

Схема, представленная на рисунке 4, обеспечивает расчет режимов работы и проверку схемы с учетом нагрузки и переключения во время полета.

Модель уровня 2

В модель синхронного генератора относительно модели первого уровня добавлены:

  • расчет модели на основе упрощенных уравнений Парка-Горева;

  • учет характеристики холостого хода;

  • возможность подключения первичного двигателя (авиационный привод);

  • блок релейных защит и управления.

В основе модели синхронного генератора лежат упрощенные уравнения Парка-Горева, позволяющие рассчитывать электромагнитные и электромеханические переходные процессы с учетом изменения периодической составляющей тока генератора.

Модель генератора представляет собой трехлинейную систему управляемых ЭДС \dot{E}_A,\dot{E}_B,\dot{E}_C,за переходным сопротивлением x_d'и активным сопротивлением статора генератора R_{CT}.Входными параметрами для расчета значений ЭДС \dot{E}_A,\dot{E}_B,\dot{E}_Cявляются фазные токи генератора \dot{I}_A,\dot{I}_B,\dot{I}_C.Расчеты выполняются независимо для каждой последовательности токов и ЭДС, причем для прямой последовательности решаются уравнения Парка-Горева в dq координатах. Вследствие этого токи и ЭДС проходят преобразования между системами «ABC», «12» и «dq».

Общая структура модели синхронного генератора представлена на рисунке 5

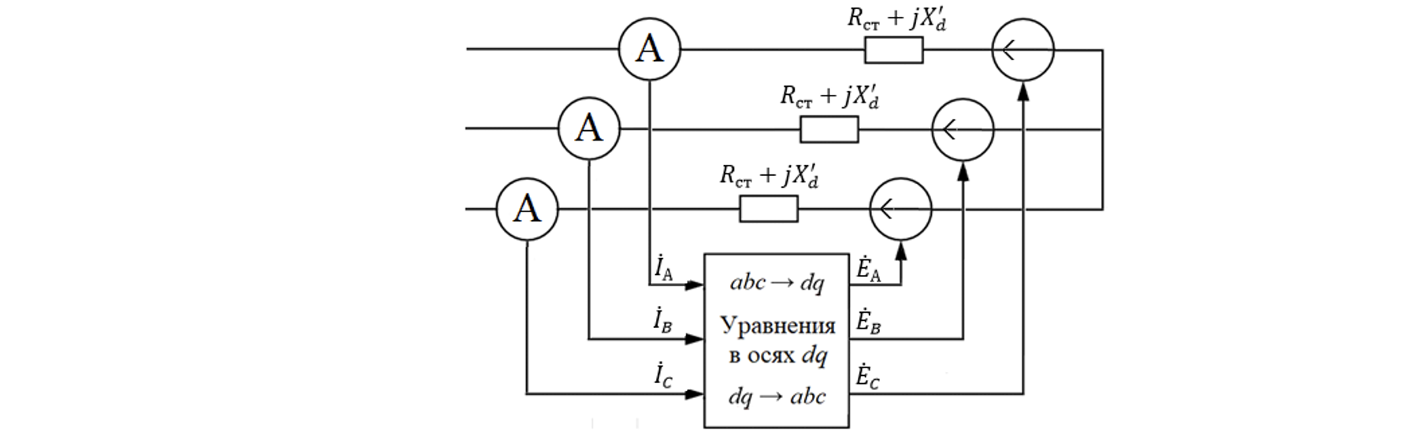
Рисунок 5 – Структура модели синхронного генератора уровня 2.
Рисунок 5 – Структура модели синхронного генератора уровня 2.

Таблица 2 – Исходные данные для расчета параметров модели синхронного генератора уровня 2

Наименование свойства

Обозначение

Номинальная мощность, Вт

Snom

Номинальное напряжение, В

UnomPh

Номинальный коэффициент мощности, о.е.

cosφ

Номинальная частота, Гц

fnom

Номинальная частота вращения, об/мин

Nnom

Сопротивление обмотки статора, о.е. 

X2

Индуктивное сопротивление по продольной оси, о.е.

Xd

Переходное сопротивление, о.е.

X'd

Индуктивное сопротивление по поперечной оси, о.е.

Xq

Постоянная времени обмотки возбуждения при разомкнутой обмотке статора, с

Td0

Ток возбуждения холостого хода, А

Ifx

Ток возбуждения (массив), о.е.

Inamag

Напряжение на выводах генератора (массив), о.е.

Unamag

Начальная скорость вращения, о.е.

w_start

Ток прямой последовательности статора \dot{I}_1,ток обратной последовательности \dot{I}_2и ток нулевой последовательности \dot{I}_0определяются на основании комплексных значений фазных токов генератора \dot{I}_A, \dot{I}_B,\dot{I}_c по формулам:

\dot{I}_1=\frac{1}{3}\left( \dot{I}_A+\dot{\alpha}\dot{I}_B+\dot{\alpha}^2\dot{I}_C \right);\\ \dot{I}_2=\frac{1}{3}\left(\dot{I}_A+\dot{\alpha}^2\dot{I}_B+\dot{\alpha}\dot{I}_C\right);\\ \dot{I}_0=\frac{1}{3}\left(\dot{I}_A+\dot{I}_B+\dot{I}_C \right);

где \dot{\alpha}- оператор перевода равные e^{j\cdot 120}.

Преобразование токов прямой последовательности генератора от фазных координат к dq и обратное преобразование ЭДС прямой последовательности осуществляется следующим образом:

I_d=Im(\dot{I}_1)cos(\delta_Г)-Re(\dot{I}_1)sin(\delta_Г);\\I_q=Im(\dot{I}_1)sin(\delta_Г)+Re(\dot{I}_1)cos(\delta_Г);\\Im(\dot{E}_1)=E'_qsin(\delta_Г)+E'_dcos(\delta_Г);\\ Re(\dot{E_1})=E'_qcos(\delta_Г)-E'_dsin(\delta_Г);

где: I_d,I_q – токи статора генератора в dq координатах; \dot{E}_1– ЭДС прямой последовательности статора генератора в фазе А; E_d',E'_q– переходные ЭДС генератора в dq координатах; ????г – угол положения ротора.

Так как ЭДС модели генератора вынесены за переходное сопротивление X'_d,в общем случае не равное сопротивлению обратной последовательности X_2и нулевой последовательности X_0в ЭДС генератора кроме \dot{E}_1вводятся добавочные ЭДС \dot{E}_2,\dot{E}_0 определяемые по формуле:

\dot{E}_2=\dot{I}_2\cdot j(X'_d-X_2);\\\dot{E}_0=\dot{I}_0\cdot j(X'_d-X_0).

С учетом \dot{E}_2 и \dot{E}_0значения фазных ЭДС генератора равны:

\dot{E}_A=\dot{E}_1+\dot{E}_2+\dot{E}_0;\\\dot{E}_B=\dot{\alpha^2\dot{E}_1+\dot{\alpha}\dot{E}_2+}\dot{E}_0;\\ \dot{E}_C=\dot{\alpha}\dot{E}_1+\dot{\alpha}^2\dot{E}_2+\dot{E}_0.

Переход от именованных единиц к относительным единицам для тока осуществляется делением на номинальный ток генератора, обратный переход к именованным единицам для ЭДС – умножением на номинальное напряжение генератора UnomPh.

Уравнения модели генератора в относительных единицах в dq координатах выглядят следующим образом: 

E'_q=\frac{1}{s \cdot T_{d0}}(E_f-(X_d-X_d')\cdot I_d),

где E_f- ЭДС обмотки возбуждения.

Характеристика холостого хода учитывается если свойству «Учитывать характеристику XX» присвоено значение «Да».

Характеристика холостого хода учитывается добавочной ЭДС \Delta E_I, определяемой выражениями:

\Delta E_I=V_{unsat}(I_{FD})-V_{sat}(I_{FD})=I_{FD}-V_{sat}(I_{FD}),

где Vunsat – напряжение статора генератора без учета насыщения (в относительных единицах численно равно току возбуждения генератора IFD), Vsаt – напряжение генератора в соответствии с характеристикой холостого хода.

Уравнение движения генератора имеет вид:

\frac{d\omega}{dt}=\frac{1}{T_J}(M_t-M_e)=\frac{1}{T_J}(M_T-(\Psi_dI_q-\Psi_qI_d));\\\frac{d\delta_Г}{dt}=\omega_0\omega;

где: \omega – относительная скорость вращения ротора генератора; ????г – угол положения ротора, T_J– постоянная инерция агрегата, M_t – момент первичного двигателя; M_eэлектромагнитный момент; \omega_0– синхронная угловая частота вращения.

Уравнение движения не используется, если от первичного двигателя берется скорость вращения, а не момент.

Модель синхронного генератора имеет порт «Eng» предназначенный для подключения блока первичного двигателя (привода авиационного генератора). Порт служит для приема с первичного двигателя сигналов: скорости вращения ωEng или момента M_t, температуры Tmp и давления масла P ривода, и для обратной передачи скорости вращения ротора генератора \omegaили механической мощности генератора Nel.

Для корректной модели второго уровня нам также необходимо наличие модели привода авиационного генератора. Приведем пример самого простого варианта, свойства которого представлены в таблице 3, где задаются номинальные параметры привода.  

Таблица 3 – Исходные данные для расчета модели привода авиационного генератора 

Наименование свойства

Обозначение

Рабочий диапазон частот вращения входного вала [nмин, nмакс], об/мин

nrabdiap

Частота вращения выходного вала (nном), об/мин

nnom

Максимальная механическая мощность (Nмакс), кВт

Nmax

Коэффициент полезного действия

Eff

Рабочая температура, °С

Tmp

Рабочее давление

Prab

Задержка времени на расцепление вала, с

DiscT

Закон регулирования частоты выходного вала привода основан на следующих выражениях: 

\left \{ \begin{align} n_{вых}&=n_{вх}, при \ \ n_{вх}< n_{rabdiap}(мин);\\ n_{вых}&=n_{nom}, при \ \ \ n_{rabdiap}(мин)\le n_{вх}\le n_{rabdiap}(макс);\\ n_{вых}&=0, при \ \ n_{вх}>n_{rabdiap}(макс) \ \ или \ \ N_{вх} >N_{maх}; \end{align} \right.

где: n_{вх}- входная частота вращения привода; N_{вх}- входная мощность привода.

Для передачи блоку значения частоты вращения предусмотрен входной порт «nвх». Для выдачи сигнала первичного двигателя на генератор предусмотрен выходной порт «Eng». 

При значении свойства блока «Внешний сигнал задания температуры» равному «Да» у блока для передачи ему значения температуры появляется входной порт «Tmp». При значении «Нет» значения задаются из свойств. Аналогичным образом выполнено свойство «Внешний сигнал задания давления масла» с портом «P». При значении свойства блока «Внешний на расцепление вала» равному «Да» у блока для передачи ему соответствующего значения появляется входной порт «disc».

Сигналы температуры и давления необходимы для функционирования защит и предназначены для направления к блоку генератора, в блок регулирования, защиты и управления (БРЗУ) где на их основе функционируют защиты. 

Блок регулирования, защиты и управления генератором

Для регулирования синхронного генератора в блоке реализован ПИД-регулятор. В блоке реализованы защиты, представленные в приложении А.

Срабатывание защит c возможностью возврата в исходное состояние регистрируется с выводом сборного сигнала в память. Для управления включением и отключением БРЗУ предусмотрен входной порт «Com». Для выдачи сигнала на расцепление привода генератора предусмотрен выходной порт «disc». Для подключения необходимых величин (токов и напряжений) предусмотрен входной порт «Par_pr». Для управления контактором имеется выходной порт «C_KM» и дополнительный входной порт «KM_вспом», необходимый для проверки отказов.

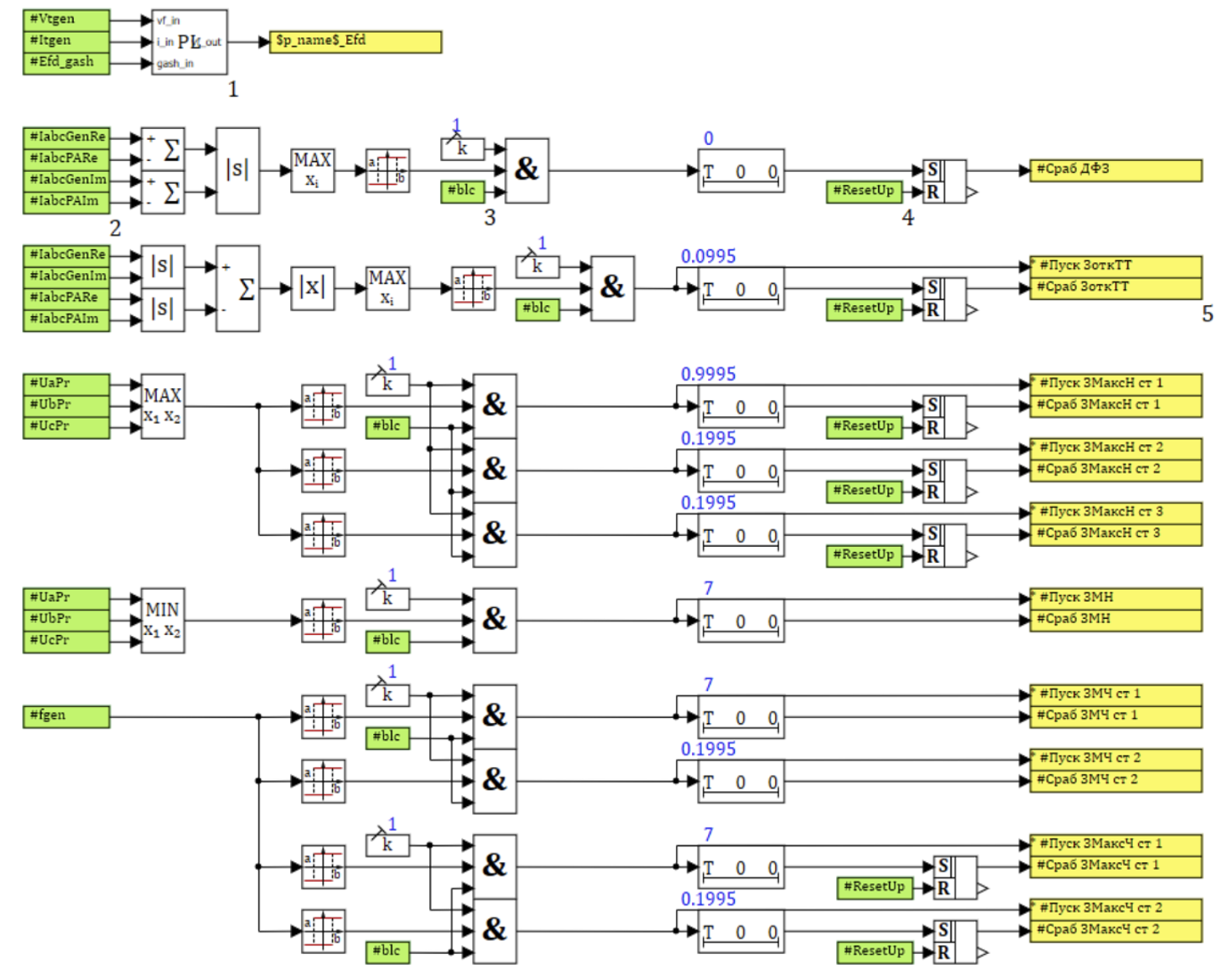
Рисунок 6 – Субмодель БРЗУ с логикой части защит: 1 – блок программирования, в котором реализуется логика ПИД-регулятора; 2 – входные величины; 3 – сигнал блокировки при снятии питания с БРЗУ; 4 – сигнал перезагрузки после подачи питания на БРЗУ; 5 – входные сигналы защит.
Рисунок 6 – Субмодель БРЗУ с логикой части защит: 1 – блок программирования, в котором реализуется логика ПИД-регулятора; 2 – входные величины; 3 – сигнал блокировки при снятии питания с БРЗУ; 4 – сигнал перезагрузки после подачи питания на БРЗУ; 5 – входные сигналы защит.
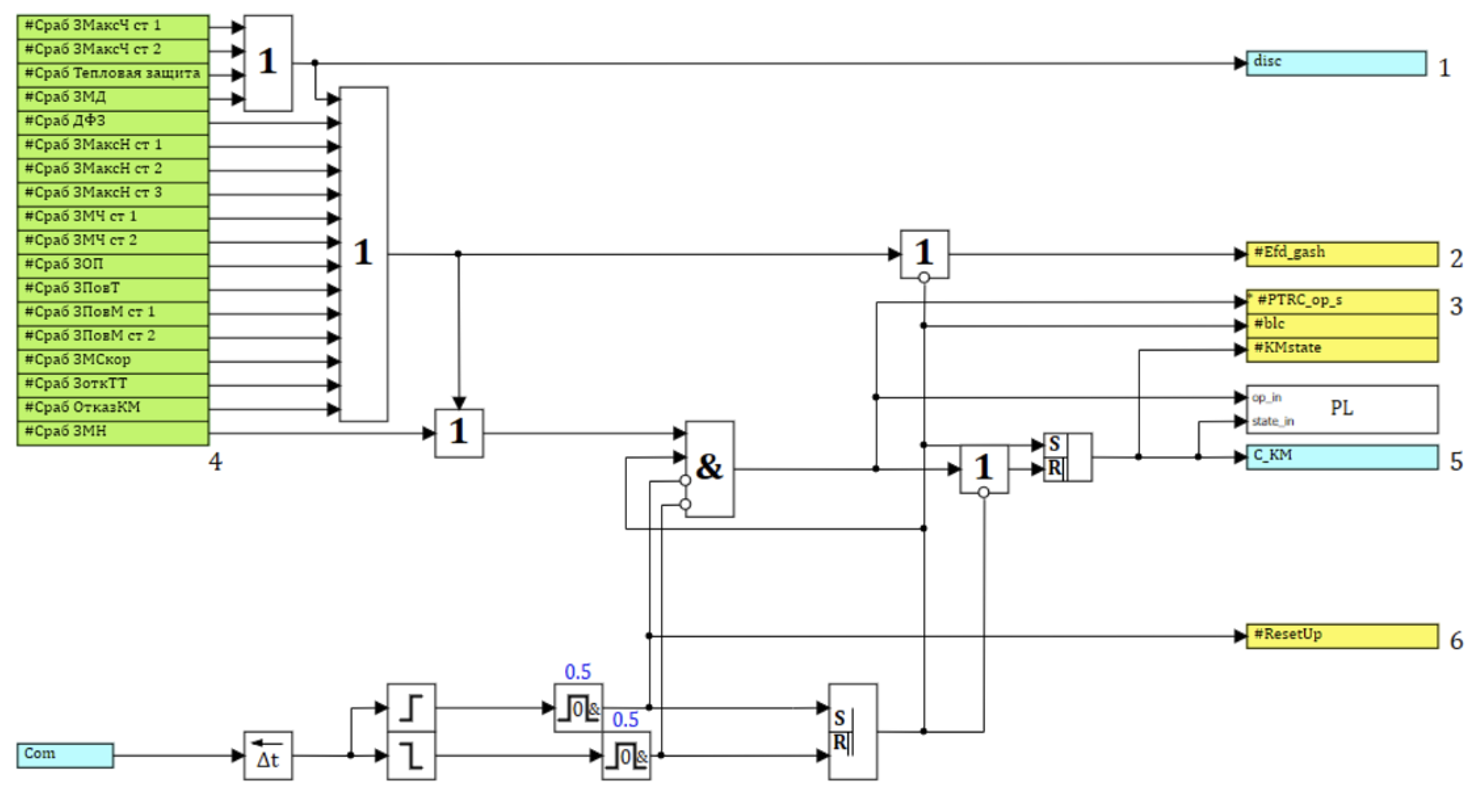
Рисунок 7 – Субмодель БРЗУ с логикой управления: 1 – сигнал на отключение привода генератора; 2 – сигнал на гашение поля генератора; 3 – сборный сигнал защит; 4 – выходные сигналы защит; 5 – сигнал управления, выводимый на порт блока; 6 – сигнал перезагрузки после подачи питания на БРЗУ
Рисунок 7 – Субмодель БРЗУ с логикой управления: 1 – сигнал на отключение привода генератора; 2 – сигнал на гашение поля генератора; 3 – сборный сигнал защит; 4 – выходные сигналы защит; 5 – сигнал управления, выводимый на порт блока; 6 – сигнал перезагрузки после подачи питания на БРЗУ

В свойствах блока (см. рисунок 8) выделена возможность активации и деактивации каждой из защит, установка параметров зоны их срабатывания и возврата, установка значения базисного тока для токовых защит, а также начальное состояние контактора.

Рисунок 8. Свойства блока регулирования защиты и управления генератором.
Рисунок 8. Свойства блока регулирования защиты и управления генератором.

Модель второго уровня для корректной работы уже требует подключения блоков привода и БРЗУ, и минимально рабочая схема принимает вид как на рисунке 9:

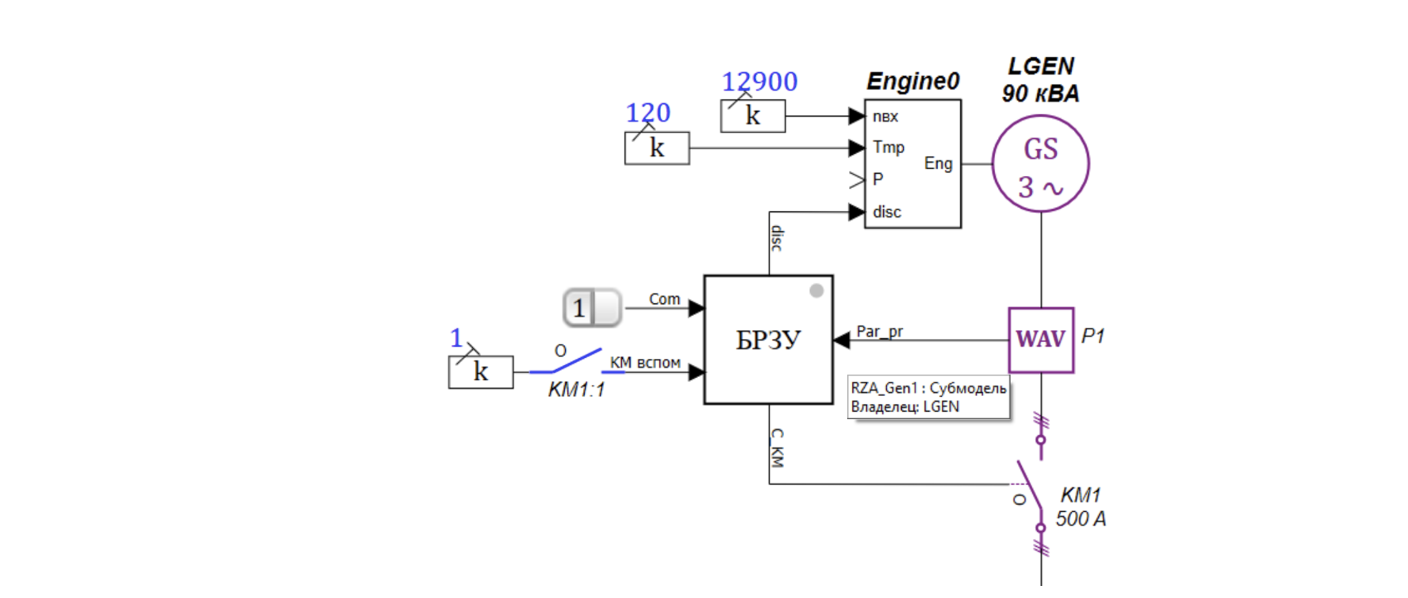
Рисунок 9. Схема модели генератора уровня 2
Рисунок 9. Схема модели генератора уровня 2

Повысив уровень моделирования, мы существенно усложнили математическую модель, и система СЭС сегмента переменного тока модели первого уровня, представленная на рисунке 3, будет выглядеть как показано на рисунке 10:

Рисунок 10. Схема типовой двухканальной СЭС модели второго уровня: сегмент переменного тока.
Рисунок 10. Схема типовой двухканальной СЭС модели второго уровня: сегмент переменного тока.

На втором уровне моделирования выполняется анализ динамических процессов - изменения параметров во времени, поэтому блок управления в модели данного уровня уже содержит реальные алгоритмы защиты и управления, готовые к загрузке в контроллер управления. 

Данная модель позволяет произвести тестирование алгоритмов защит как в локальном режиме, задавая воздействия и анализируя результат работы защит, так и в процессе комплексного моделирования полной схемы электрических систем самолета или комплексной мультифизической модели самолета.

На рисунке 11 представлена модель в генераторе с блоком БРЗУ для локального моделирования работы защит.

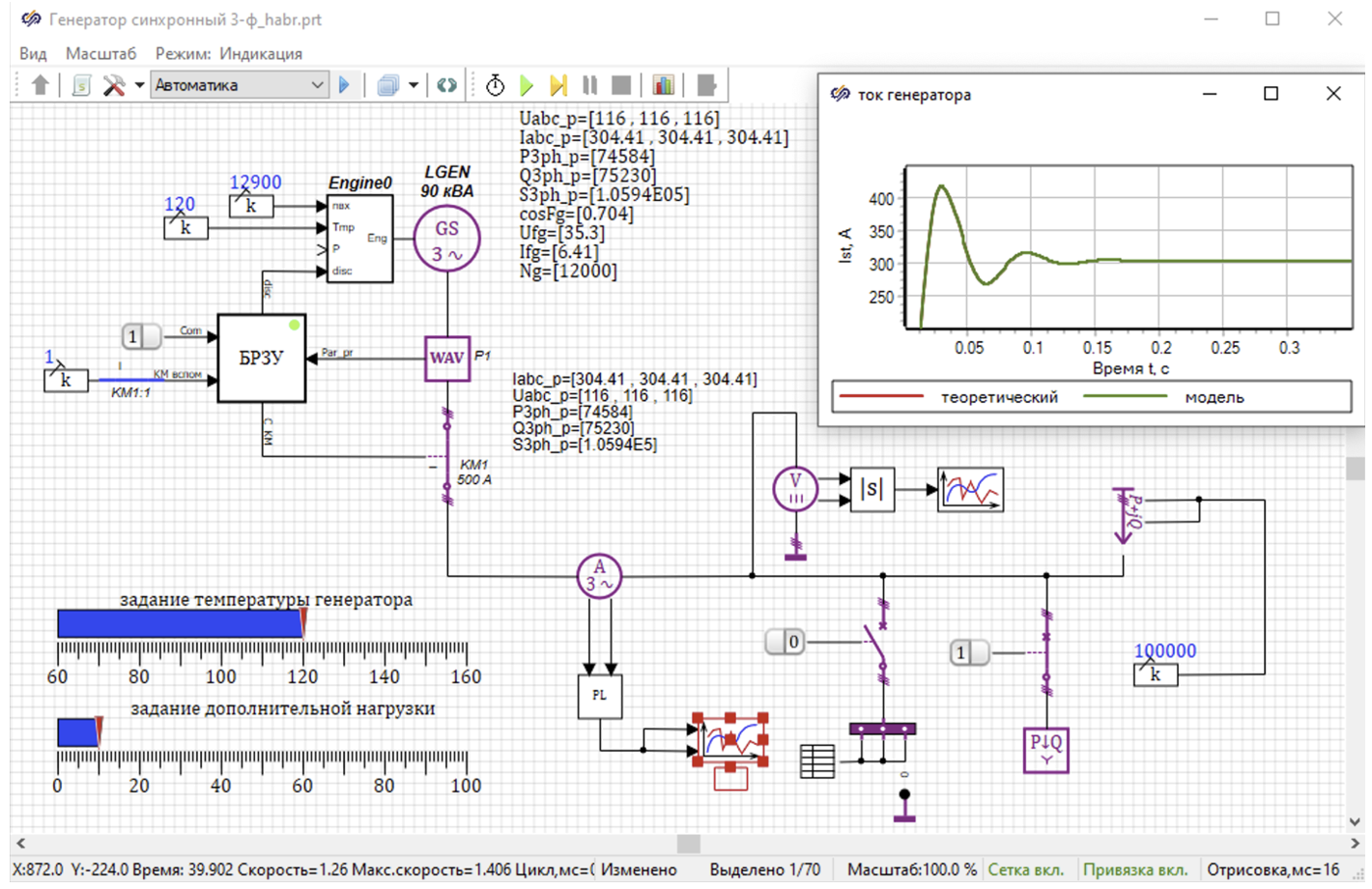
Рисунок 11. Модель для проверки работы систем защиты генератора
Рисунок 11. Модель для проверки работы систем защиты генератора

Данная модель позволяет задавать во время моделирования в ручном режиме температуру генератора, мощность нагрузки, а также отключать нагрузку и создавать короткое замыкание. Модель, отлаженная в локальном режиме, в дальнейшем используется в полной модели для проверки работы в режиме полета.

Модель 3-го уровня

На 3-м уровней моделирования выполняется расчет в мгновенных значений параметров тока в каждой фазе системы. Такое моделирование требует значительно более высокой частоты вычислений. Нам необходимо получить разрешения по времени, обеспечивающие хотя бы 10 точек на один период синусоиды тока, при частоте авиационного генератора 400 Гц.

Практический пример третьего уровня моделирования рассмотрен в статье «Модельно-ориентированное проектирование. Электропривод с бесколлекторным двигателем постоянного тока».

Выводы

Уровень математических моделей при модельно-ориентированном подходе может быть разным.

Уровень математических должен соответствовать стадии проектирования, на котором используется модель.

Создание библиотек моделей соответствующего уровня является отдельной задачей в рамках создания цифрового двойника изделия, но в результате обеспечивает ускорение процесса проектирования и повышения качества принимаемых проектных решений.

Пример модель генератора второго уровня можно взять здесь.

Видео с демонстрацией процесса тестирования модели:

Комментарии (6)


  1. Novostnik
    29.04.2022 10:33
    #24306746
    +1

    При создании таких моделей используется целый ряд допущений. Также присутствуют погрешности вычислений. Отсюда два вопроса:

    1. Какой в этом практический смысл?

    2. Где тут собственно двойник? Если двойник - это мат. модель, то где тут "первик"?


    1. petuhoff Автор
      29.04.2022 13:45
      #24307404

      Второй вопрос я всегда сдвал авторам нашего стандата о "цифровых двойников" и господин Боровков меня даже забанил в фейсбуке. Поэтому в стандарте и используется кривая конструкция что-то "компьютерная модель звязаная двухсторонниим информационными связями с объекта, В СЛУЧАЕ ЕГО НАЛИЧИЯ"

      По первому вопроссу практический смысл как раз очень большой быстро собррать схему, загрузить полетное задание и проверить ее на работоспособность, а так же выбрать основные необхожимы параметры генераторов. Сильно ускорряется первая часть проектирования.


      1. Novostnik
        29.04.2022 14:40
        #24307616
        +1

        Суть моего вопроса была в том, что если нет физического объекта, то и практического смысла нет. Результат моделирования говорит о том, что данная программа умеет решать некие уравнения, но нельзя надеятся, что потом кто-то спроектирует физическую систему по этим результатам и она сразу заработает.


        1. petuhoff Автор
          29.04.2022 15:30
          #24307756

          Именно для того, что бы система заработала и решаются данные уравнения, они же отражают физику процессов, поэтому прежде чем что то проектировать нужно сначала произвести расчеты. Поэтому объект появляется уже после формул и расчетов.

          Если говорить о конкретном примере, то электрическая система из модели в дальнейшем превращается в реальную электрическую систему электроснабжения для авиации.


      1. Ndochp
        29.04.2022 16:04
        #24307808
        +1

        Ну то есть в этой работе пропущен момент обратной связи для коррекции двойника и алертинга.


        Грубо говоря, вот есть спутниковая система ГЛОНАС, она передает в эфир данные своего цифрового двойника, и приемное устройство абонента по этим данным вычисляет свои координаты.
        Но двойником эту штуку делает не [только] продвинутая мат модель спутника, вращающегося вокруг Земли. Но и сеть наземных станций, выполняющих реальные измерения положения спутников. По этим измерениям модель ежесуточно корректируется, и остается двойником.


        В статье кажется все-таки какая-то САПР модель, а не двойник.


        Хотя возможно это дурацкий спор о терминах.


        1. petuhoff Автор
          29.04.2022 16:33
          #24307880

          Я согласен полностью, и само слово двойник в западноим понимании цифрового двойника, говорит о существование реального физического оригинала. Но поскольку тему цифрового двойника в РФ оседлали разработчики математических моделей, они натянули сову на глобус и применяют термин "цифровой двойник" и на стадиях когда реальный объект еще только проектируется. В процесс проектирования используется несколько разных моделей (примеры из статьи) ктоторые собрали в кучу и назвали "цифровым двойником". Хотя по моему мнению, реальны "цифровым двойником" становится модель последней стадии, которая отлаживается по реальным данным испытаний или даже эксплуатации.