Или новый ключик к одной из проблем тысячелетия.

От автора

В статье рассказывается о подходе к анализу распределения простых чисел. О подходе с использованием новой выведенной формулы распределения чисел для всего натурального ряда. Статья по большей части написана простым, не научным языком, а потому даже школьник старших классов с минимальным набором знаний будет способен запросто ее понять. Кроме этого, в простом ключе статья написана еще потому что, автор полученной формулы и самой статьи не является ученым, научным сотрудником, студентом. Просто любитель, с неоконченным высшим образованием. Просто веб-разработчик и дизайнер интерфейсов, решил на досуге, ради интереса попробовать разобраться с дзета-функцией Римана и случайно наткнулся на лежащий под ногами клад.

Прошу научное сообщество не судить строго стиль изложения, и простить мне некоторую вольность, как и возможные неточности. Повторюсь, я не математик… Поверьте, просмотрел кучу источников, в надежде найти подобную формулу, дабы не заниматься написанием этой статьи, не тратить свое время и время других. И не нашел… (искал по тематической литературе, индексируемым публикациям в научных журналах на elibrary.ru) А поскольку важность найденной формулы распределения чисел весьма высока, то я просто обязан поделиться ею с сообществом.

Если честно, то никогда бы не подумал, что случится подобное.

Предисловие. Или для чего нужны простые числа

С точки зрения арифметики большинство чисел отличается, так сказать, «хорошим поведением». Четные числа всегда чередуются с нечетными, каждое третье число всегда кратно трем, квадраты чисел подчиняются определенному закону. Поэтому мы можем составить длинный ряд чисел, которые ведут себя так, как им положено, независимо от длины этого ряда и величины самих чисел. Но простые числа похожи на неуправляемую толпу. Они появляются там, где им захочется, без предварительного предупреждения, на первый взгляд, совершенно хаотично, без какой-либо закономерности. А самое главное — их нельзя проигнорировать: простые числа необходимы для арифметики и для математики в целом.

Простые числа — не такая уж сложная тема, на изучение которой потребовалось бы много лет; фактически ее проходят еще в школе. Чтобы понять, что такое простое число, нужно лишь уметь считать и владеть четырьмя основными арифметическими действиями. Тем не менее, простые числа были и продолжают оставаться одной из самых удивительных проблем в истории науки. Тот, кто хочет заниматься математикой, но не владеет теорией простых чисел, ничего не сможет добиться, так как они присутствуют везде — иногда затаившись, как в засаде, готовые появиться, когда их меньше всего ожидаешь. С неизбежностью появления простых чисел невозможно не считаться.

Простые числа важны не только в математике. Многие даже не догадываются о том, что они играют важную роль в нашей повседневной жизни, например, в банковских операциях или в обеспечении защиты персональных компьютеров и конфиденциальности разговоров по мобильному телефону. Они являются краеугольным камнем компьютерной безопасности.

Источник. (Простые числа [Долгая дорога к бесконечности]. Грасиан Энрике)
По ссылке выше находится весьма интересная статья, про простые числа. Тем кто плохо знаком с темой — настоятельно рекомендую!

Загадки распределения простых чисел, всегда будоражили умы многих выдающихся математиков: Эйлер, Ферма, Гаусс, Риман и многие многие другие, пытались разгадать сей загадочный пазл. До сих пор, существует множество гипотез и нерешенных вопросов, которые связанны с простыми числами, и которые остаются неизученными:

Пожалуй, понятно насколько было велико мое удивление, когда вывел формулу и стало ясно, что аналогов (кроме дзета-функции Римана) похоже что нет. Что же, теперь настало время поговорить о самой формуле, которая приоткрывает загадочную завесу тайны в распределении простых чисел: предоставляет инструмент для дальнейшего анализа — иной способ факторизации числа.

Очень надеюсь, что специалисты в области теории чисел и криптографии будут довольны!

Вступление

Посмотрите, на эти хаотичные, на первый взгляд, движения точек. Но нет, это далеко не Броуновское движение. Эти движения раскладывают на множители любое натуральное число или показывают расположение простого числа… Любопытное зрелище. Длиною в бесконечность и историей в без малого 2000 лет (первый известный алгоритм поиска простых чисел — Решето Эратосфена, 273–194 до н. э.):

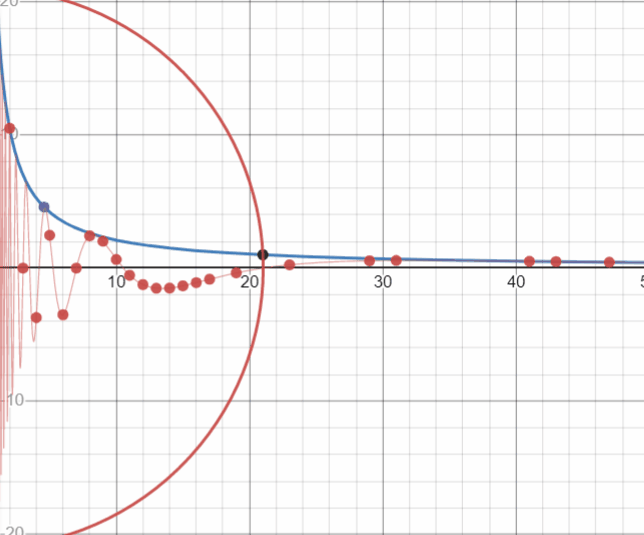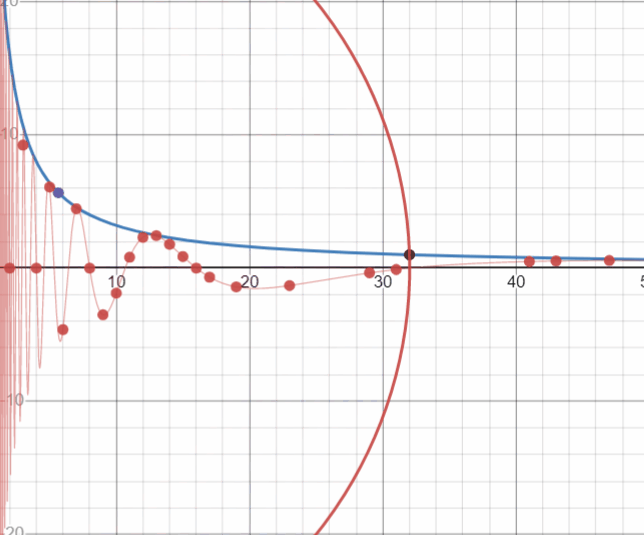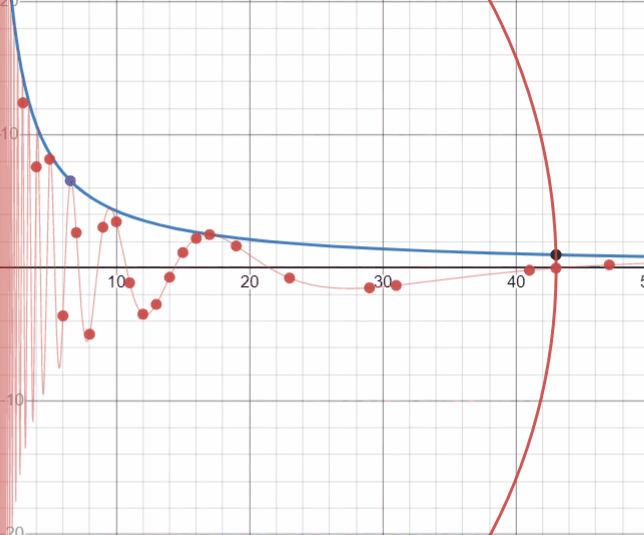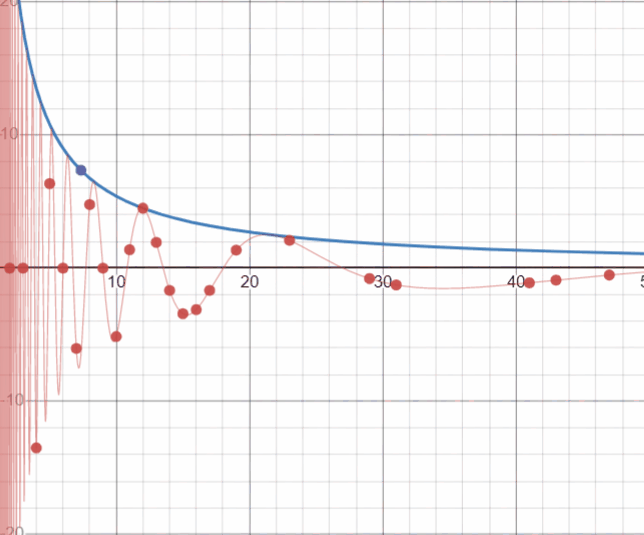
Вот, например, точки находятся на оси абсцисс — значит это множители числа а=12:

A здесь нет пересечений точек с целой координатой х, или иначе — нулей функции.
Перед нами простое число:

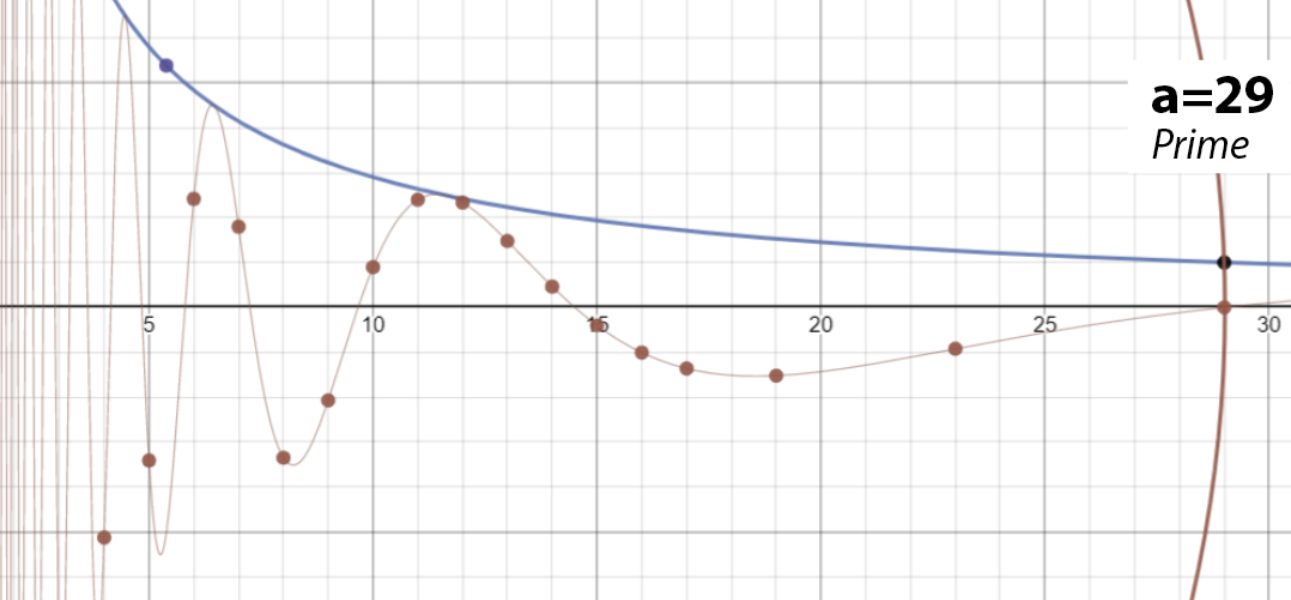
Гипотеза о распределении нулей натурального ряда

Итак, формула имеет следующий вид:

Где:
, заданное число.

Теперь о свойствах функции:

• Если результат уравнения , то значит, такое число является множителем числа а.

• Каждое пересечение синусоиды с осью ОХ, является показателем кратности числа а.
  Так, если a=12, то и т.д.

• Очевидно, что на периодах (между пересечениями) (На рисунке, это интервалы 1/2, 1/3, и т.д. соответственно), y функции нет нулей.

  — Свойств у функции, скорее всего больше. Нужно, проводить более тщательный анализ.

  Для упрощения алгоритма разложения числа на множители, коэффициент перед синусом можно убрать. Т.е. формула определяет нули и их отсутствие
  в таком виде:
  
  

  Факторизовать таким способом большие числа, по понятным причинам — не рекомендую. Для этого есть нормальные алгоритмы.

Гипотеза о предсказании появления простых чисел

Можно заметить, как свободные члены, не занятые в построении числа выстраиваются в ряды по некоторой траектории:

И действительно, они всегда занимают свободные “орбитали” (на рис. светло-зелёные линии)

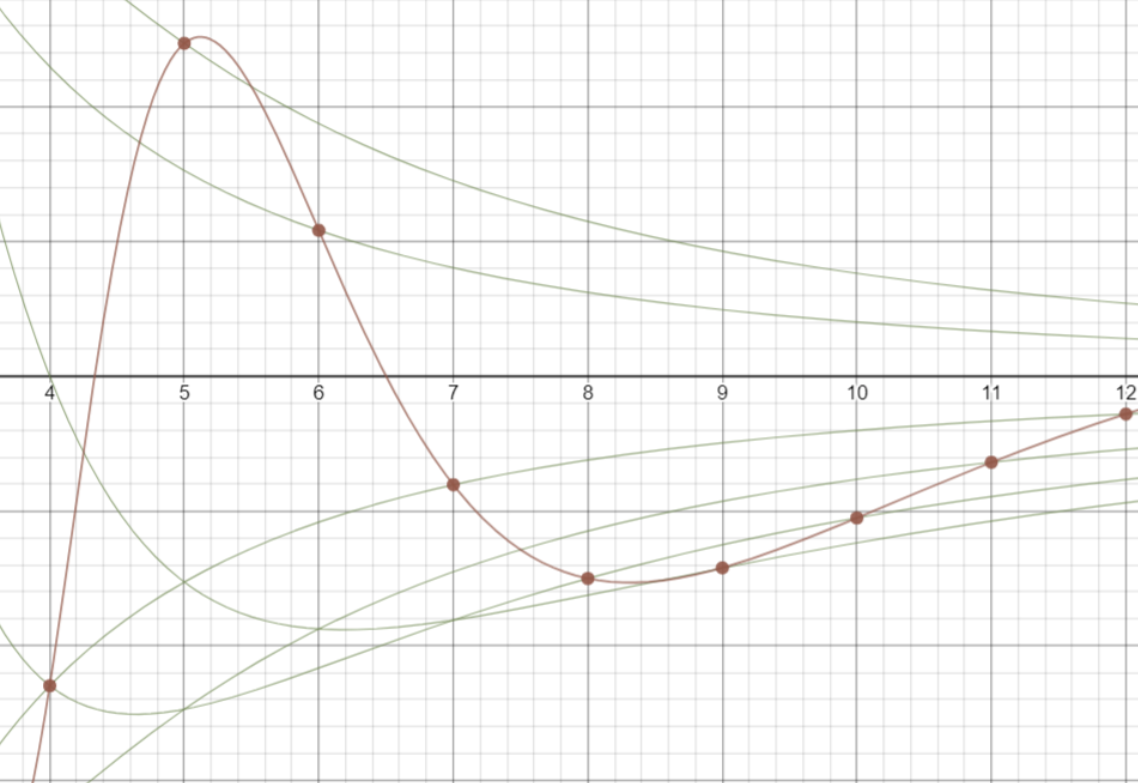
Формирование орбиталей

Введу несколько терминов:
Положительная орбиталь, - орбитали которые находятся выше оси ОХ.
Отрицательная орбиталь, - ниже оси, соответственно.

Итак, положительная орбиталь порождается каждый раз при:
a mod 5 = 0 (или когда начало периода 1/5 — становится нулем)
Отрицательная орбиталь создается при:
a mod 3 = 0 (или когда начало периода 1/3 — становится нулем)

Так, например, если a=19, то

Каждая из орбиталей задается формулой:

где или иными словами:

В общем, если имеем число a = 41, то всего орбиталей будет:
плюс — Ось нулей

По ходу расширения числовой оси (увеличения числа а), члены перепрыгивают на следующие орбитали, в сторону начала координат. Таким образом, иcходя из их поведения, гипотетически, можно спрогнозировать появление следующего простого числа.

Попытаемся, графически предсказать проявление следующего простого числа, при a=22. Изобразим стрелками на какие орбитали сместятся числа для а+1=23

Вот так. Смотрим на позиции чисел на орбиталях и на то куда перейдут эти числа (на следующем шаге или через n-шагов с учетом добавления новых орбиталей), и предсказываем появление следующего простого числа, зная, что при простом числе нули будут отсутствовать.

Что же, похоже на то, что к математической загадке найден очередной ключик. Осталось, пожалуй, найти строгое доказательство всему этому добру. Да более детально исследовать все особенности поведения функции, скачков чисел (так и хочется сказать — электронов) по орбиталям. Пожалуй, что предоставлю сие удовольствие более серьезных исследований и открытий связанных с изучением функции — Математикам, специалистам по теории чисел и анализу, а так же всему научному сообществу!

→ Поиграться с функцией можно здесь: desmos.com

Заключение

Хотя к поведению простых чисел и найден очередной ключик, но не стоит сильно радоваться. Факторизация по прежнему остается сложной задачей для больших чисел, а чтобы предсказать появление очередного нового простого числа — придется передвинуть очень много элементов по орбиталям.

И тем не менее, если гипотеза Римана делает предположение о нулях, то здесь на более простом (школьном) уровне делается предположение о способе предсказания нулей. А это, в свою очередь, позволяет применить более широкий арсенал математических методов для более глубокого изучения простых чисел.

Надеюсь, что более детальное исследование специалистами данной функции позволит сделать еще массу полезных и удивительных открытий в теории чисел. Как и все заинтересованные буду ждать новых исследований и достижений!

В заключение слова благодарности

Спасибо авторам YouTube каналов, которые смогли заинтересовать математикой. Без вас и вашей мотивации я навряд ли бы полез разбираться с данной темой.

Алексей Саватеев
3blue1brown