Матрицы и заключение.

Завершающий урок из цикла про линейную алгебру для 3D-приложений от Александра Паничева — ведущего разработчика логики в UNIGINE. В прошлом уроке мы разобрали углы Эйлера и кватернионы, а в этот раз поговорим о матрицах и подведем итоги.

Матрицы

Проще говоря, матрица в 3D-графике — это массив чисел, расположенных по строкам и столбцам:

В 3D-приложениях используются матрицы либо размером 3х3 (матрицы вращения), либо 4х4 (матрица трансформации). Рассмотрим матрицу 4х4 (трансформацию).

В первых трех столбцах находится вращение (Rotation), которое представлено в виде трех ортогональных друг к другу векторов (ось вправо, ось вперед, ось вверх), а по диагонали масштабирование (Scale).

Почему так? Смотрите предыдущую лекцию. Все дело в самой природе комплексных чисел.

В четвертом столбце — смещение (Translation). А единица под смещением — это гомогенная координата. Если она равна 1 — позволяет сдвигать вектор перемножением матриц. А если равна 0 — Translation считается вектором направления.

Как правило, для удобства работы все объекты в виртуальном мире формируются в определенные иерархии. Такие иерархии называются родительско-дочерними связями.

Например: пистолет в руке главного героя. «Пистолет» является дочерним к объекту «герой».

Когда мы выбираем объекты в 3D-редакторе, в инспекторе объектов справа вверху всегда видна локальная матрица трансформации (декомпозиция локальной матрицы). В ней Position, Rotation и Scale показываются относительно родителя. То есть родитель становится центром начала координат.

1. Родительско-дочерняя связь с точки зрения кода и матриц реализуется как:

world_B = world_A * local_B
local_B = inverse(world_A) * world_B

Где world_A — глобальная (родительская) матрица трансформации, скажем, «героя».

local_b — локальная (дочерняя) матрица, к примеру, «пистолета».

world_b — это ее глобальная (мировая) матрица трансформации.

2. Узнать положение точки (vec3_world_position_B) относительно «глаз» объекта A:

vec3 relative_pos_B = inverse(world_A) * vec3_world_position_B;

3. Связь с камерой:

view = inverse(transform)

где transform — матрица трансформации камеры,

view — матрица, которая необходима для перевода вершины какой-либо модели в экранное пространство (читаем про тройку преобразований model * view * projection).

4. Детерминант mat3 — это объем параллелепипеда из XYZ осей со знаком.

5. Ранг mat3 — проверка на «схлопывание» базиса в плоскость (2) или в линию (1).

6. Транспонирование — перевод столбцов в строки:

transpose(mat3) == inverse(mat3)

Если базисные вектора ортогональны и единичной длины (т.е., для любой матрицы вращения или в случае mat4 — если позиция нулевая).

Собираем матрицу в движке UNIGINE

Здесь и далее мы рассказываем про то, как работает UNIGINE изнутри.

Итак, есть два пути создания матриц:

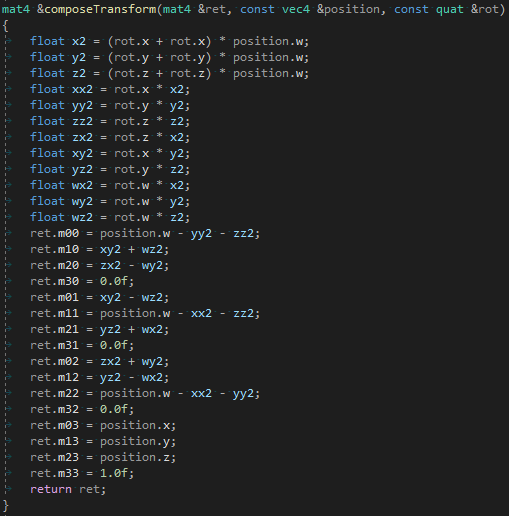
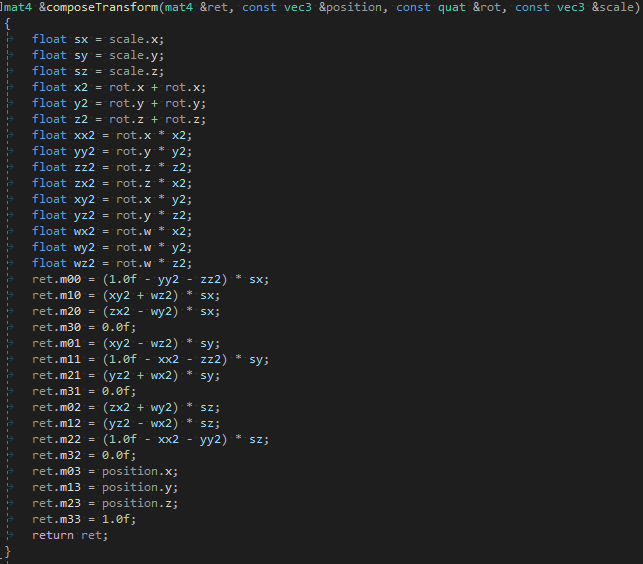
Все это быстрее, чем mat4(translate() * rotate() * scale())!

Создание матрицы масштабирования

В матрицах есть набор таких методов, как setScale (или setTranslate). Их название часто путает — можно подумать, что они задают масштаб и смещение соответственно. Но на самом деле слово set лишь означает, что мы инициализируем матрицу масштабирования (или смещения). То есть каждый метод set означает новую матрицу.

Создание матрицы вращения

Углы Эйлера в матрицу и обратно

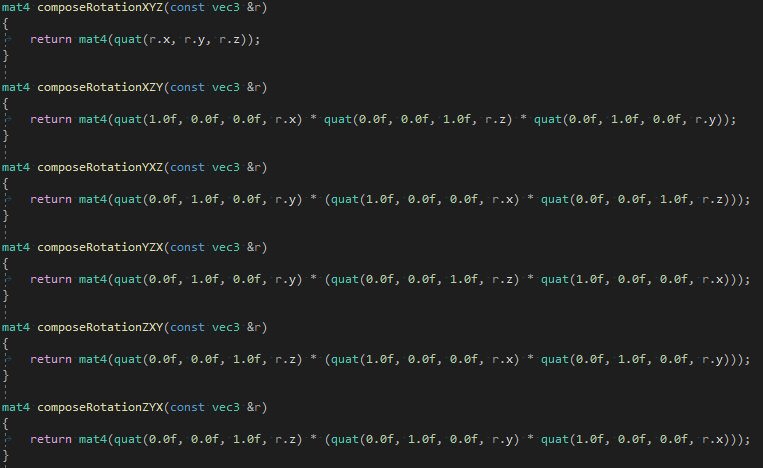
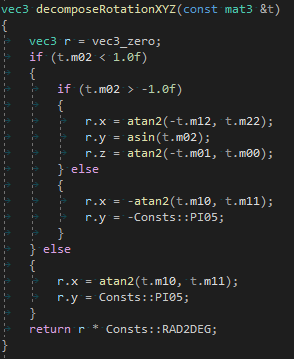
Инвертирование

Без SSE: 140 умножений, 67 сложений! Через SSE: всего 35 _mm_mul_ps. Инвертирование кватернионов все равно проще:

Заключение

Примечание редактора: на самом деле, текст снизу предназначался для первой части лекции, где не было еще кватернионов и матриц. Но, пример слишком хорош, чтобы от него отказываться, так что давайте на миг представим, что мы не читали все то, что написано выше. :)

Итак, просуммируем все то, что мы узнали в данной лекции. Рассмотрим задачу нахождения площади треугольника. Как ее лучше всего реализовать?

Как найти площадь треугольника? Вариант 1

Как найти площадь треугольника? Вариант 2

А почему?

Так, погодите-ка, а если немного оптимизнуть...

А можно сделать еще лучше?

Пару слов про SIMD (SSE, AVX):

Каков результат?

Выводы:

1. Не используем тригонометрию (sin/cos/tan) там, где этого можно избежать. Эти операции реально медленные.

2. Если есть возможность использовать length2() вместо length() — не отказываемся от этого.

3. По возможности производим операции над векторами, а не над компонентами векторов. SIMD — наш скрытый друг, товарищ и брат!

4. Ну и, самое важное: стараемся локализовать данные, с которыми работаем. Пишем cache-friendly код и все такое. Даже самая тяжелая тригонометрическая операция на порядок быстрее, чем простое взятие числа из оперативной памяти.