
Нестабильная экономическая ситуация значительно влияет почти на все сферы жизни общества и бизнеса. Меняется потребительское поведение, производственные и логистические цепочки, закупочные цены, доступность огромного количества товаров и услуг и даже состав конкурентов на рынке. Конечно, это не может не сказаться на качестве многих моделей машинного обучения, поскольку они были обучены на исторических данных, которые уже не актуальны. Это явление известно как дрейф данных или дрейф концепции и оно является основной причиной деградации модели с течением времени. Сейчас особенно полезно знать о методах детекции дрейфа и борьбы с его последствиями, ведь когда данные дрейфуют, прогнозы будут ошибочными, а решения, принятые на основе этих прогнозов, могут негативно влиять на бизнес.
В статье мы – команда Advanced Analytics GlowByte – поговорим о типах и причинах дрейфа, а также разберём на примере основные методы детекции дрейфа.
Оглавление:
По каким ещё причинам ухудшается качество работы модели
Перед тем, как мы поговорим о дрейфе, важно отметить, что он является не единственной причиной снижения качества работы модели со временем. Одной из распространённых причин может быть низкое качество входящих данных:
дубли,
пропущенные значения,
некорректные типы данных,
неверные форматы записей.
Входные данные могут быть некачественными из-за проблем с источником данных или ошибок в инженерных расчётах признаков. В этом случае для улучшения работы модели достаточно устранить или снизить влияние проблем с качеством данных.
О дрейфе данных и дрейфе концепции
В задачах машинного обучения выделяют два основных типа дрейфа: дрейф концепции и дрейф данных.
Обозначим P(Х) как безусловную вероятность входных признаков X,
P(y|Х) — как условную вероятность таргетов y при входных признаках Х.
Дрейф концепции — это изменение P(y|X), т.е. изменение зависимости целевой переменной y от признаков X. При дрейфе концепции, в отличие от дрейфа данных, распределения признаков могут остаться прежними. Иными словами, дрейф концепции происходит, когда зависимости, которым научилась модель, больше не соблюдаются. Это делает модель менее точной или даже устаревшей. Для детекции дрейфа концепции нужно обнаружить изменение в распределении целевой переменной y или изменение зависимостей y от X.
В качестве примера дрейфа концепции можно привести изменения, происходившие из-за Covid: во время пандемии люди стали отдавать большее предпочтение онлайн-обучению, спрос на губную помаду резко снизился, а штанов для йоги — наоборот, возрос в несколько раз.
Дрейф данных — это изменение P(X). По сути, это изменение входных данных, а не зависимостей между признаками X и целевой меткой y. Однако изменение P(X) может сопровождаться изменением P(y|X). Для детекции дрейфа данных нужно обнаружить изменение в распределении входных признаков X.
Пример дрейфа данных: изменение признака “частота покупок в неделю” и “средний чек”.
Немного о скорости дрейфа
Чаще всего дрейф происходит постепенно и его трудно заметить. Однако внезапные или радикальные внешние изменения могут привести к резкому дрейфу. Яркие примеры таких изменений - это пандемия Covid или внешнеэкономические санкции. Однако к резкому дрейфу могут привести и менее значительные изменения, например, закрытие одного магазина перенаправит поток клиентов в другой, что приведёт к резкому дрейфу признака “посещаемость”.
Общая концепция обнаружения дрейфа
Для того, чтобы обнаружить дрейф, необходимо сравнить 2 набора данных: исторический и новый. Методики сравнения могут быть разными, но общая схема представлена на картинке ниже:

Обнаружение дрейфа делится на несколько этапов:
Этап 1. Извлечение данных. Данные извлекаются из потока окном, поскольку по значению лишь одной точки трудно сделать вывод об общем распределении.
Этап 2. Подготовка данных. На данном этапе происходит расчёт основных характеристик данных, изменения в которых могут указывать на дрейф.
Этап 3. Вычисление оценки различия/схожести распределений. Оцениваются характеристики исторического и нового наборов данных посредством одного из методов детекции дрейфа. В результате получаем либо оценку (скор) модели, либо значение статистики какого-либо теста.
Этап 4. Принятие решения о дрейфе. Экспертная оценка дрейфа по значению статистики/скора из этапа 3.
Основные подходы к обнаружению дрейфа
Существует множество методов для детекции дрейфа данных и дрейфа концепции. С точки зрения оперативности детекции дрейфа, их можно разделить на 2 типа:
методы обнаружения дрейфа в потоковых данных,
методы обнаружения дрейфа в накопленных данных.
Методы обнаружения дрейфа в потоковых данных могут и получать на вход по одному элементу за раз (хотя рациональнее будет подавать данные небольшими пакетами) и сигнализировать о возможном дрейфе практически сразу, как он произошёл. Это достигается за счёт того, что данные методы хранят статистики данных за предыдущие временные срезы и обновляют их с получением нового элемента, принимая решение о наличии дрейфа.
Методы обнаружения дрейфа в накопленных данных получают на вход уже собранные наборы данных, поэтому фиксация дрейфа происходит постфактум.
Ниже мы рассмотрим несколько методов и протестируем их на двух синтетических потоках данных: с резким дрейфом и постепенным дрейфом.
Создание потоков данных для визуализации работы рассматриваемых методов
Для создания потока данных с резким дрейфом объединим 3 распределения по 1000 образцов в каждом:
Код
random_state = np.random.RandomState(seed=42)
data_stream_1 = random_state.normal(0.8, 0.05, 1000)
data_stream_2 = random_state.normal(0.4, 0.02, 1000)
data_stream_3 = random_state.normal(0.6, 0.1, 1000)
data_stream_abrupt_drift = np.concatenate((data_stream_1, data_stream_2, data_stream_3))Отобразим на левом графике временной ряд потока данных с резким дрейфом.
Разделим поток на 3 временных отрезка по 1000 наблюдений в каждом и отобразим график распределений этих отрезков на правом графике.

Для создания потока данных с постепенным дрейфом построим график синусоиды и добавим к нему шум.
Код
# За основу возьмем график синусоиды
y = lambda x: 1/2*np.sin(x)
x = np.linspace(-1.8, 1.5, 3000)
sin_x = y(x)
# Сгенерируем шум и добавим его к синусоиде
random_state = np.random.RandomState(seed=42)
row = random_state.normal(0.8, 0.05, 3000)
data_stream_slow_drift = row + sin_xОтобразим на левом графике временной ряд потока данных с резким дрейфом.
Разделим поток на 3 временных отрезка по 1000 наблюдений в каждом и отобразим график распределений этих отрезков на правом графике.

Методы обнаружения дрейфа в потоковых данных
Для данной задачи мы используем библиотеку River. Для удобства создадим функцию использования методов из данной библиотеки и функцию визуализации результатов работы.
Код
def stream_drift_detecton(data_stream, drift_detector, reset_after_drift=False):
"""
Функция для выявления дрейфа в потоке данных,
на выходе возвращает список с индексами элементов, на которых произошла детекция дрейфа.
data_stream - поток данных
drift_detector - метод детекции дрейфа из библиотеки River
reset_after_drift - очистить drift_detector после обнаружения дрейфа,
т.е. после детекции дрейфа все данные до дрефа в дальнейшем анализе не используются.
"""
drift_index = []
for i, val in enumerate(data_stream):
drift_detector.update(val)
# Метод update добавляет значение элемента в окно, обновляет соответствующую статистику,
# в данном случае общую сумму всех значений, среднее, ширину окна и общую дисперсию.
if drift_detector.change_detected:
# Детектор дрейфа указывает после каждой выборки, есть ли дрейф в данных
print(f'Зафиксирован дрейф на индексе {i}')
drift_index.append(i)
if reset_after_drift:
# Сброс детектора изменений
drift_detector.reset()
return drift_index
# Функция для визуализации детекции дрейфа с точками
def final_chart_dots(data_stream, drift_index, drift_values, names, abrupt_drift=False):
fig = plt.figure(figsize=(10,5), tight_layout=True)
plt.title(names['title'])
plt.xlabel(names['xlabel'])
plt.ylabel(names['ylabel'])
plt.plot(data_stream, label=names['label'], color='silver', linewidth=1)
plt.scatter(drift_index, drift_values, color='r',
label='Зона детекции дрейфа/аномалии', zorder=2, s=30)
if abrupt_drift:
plt.vlines(drift_index_fact, ymin=min(data_stream), ymax=max(data_stream),
colors='black', linestyles='dashed', lw=2,
zorder=5, label='Зона фактического дрейфа')
plt.legend()
plt.show()Adaptive Windowing (ADWIN)
ссылка на статью, ссылка на документацию
ADWIN использует метод скользящего окна для детекции изменения в распределении данных.
Концептуально он работает следующим образом:
из данных формируется окно W;
окно W делится на 2 подокна переменной длины W0 и W1, так, чтобы W0 + W1 = W;
-
рассчитывается разница в средних значениях W0 и W1 и сравнивается с определённым пороговым значением:
если дрейф зафиксирован, происходит информирование о дрейфе, а подокно W0 закрывается и больше не используется в анализе;
окно W расширяется за счёт новых поступающих значений потока данных.
Вход: может быть любым числовым значением.
Параметры:
delta: float (default=0.002), delta Є (0, 1).
Чем ближе к 1 – тем чувствительнее.
На выходе получаем индекс элемента, на котором произошла детекция дрейфа.
Работа ADWIN на потоке данных с резким дрейфом
Код
from river.drift import ADWIN
# Детекция дрейфа
drift_index_adwin_a = stream_drift_detecton(data_stream_abrupt_drift,
ADWIN(), reset_after_drift=True)
# Визуализация работы метода
drift_values_adwin_a = data_stream_abrupt_drift[drift_index_adwin_a]
names_adwin_a = {'title': 'ADWIN: детекция резкого дрейфа в потоке данных',
'xlabel': 'Time',
'ylabel': 'Значение признака x',
'label': 'Поток данных'}
final_chart_dots(data_stream_abrupt_drift, drift_index_adwin_a,
drift_values_adwin_a, names_adwin_a, abrupt_drift=True)
Как видно, ADWIN довольно быстро определил резкий дрейф.
Работа ADWIN на потоке данных с постепенным дрейфом
Код будет таким же, как и для детекции резкого дрейфа. Перейдём сразу к визуализации работы метода:
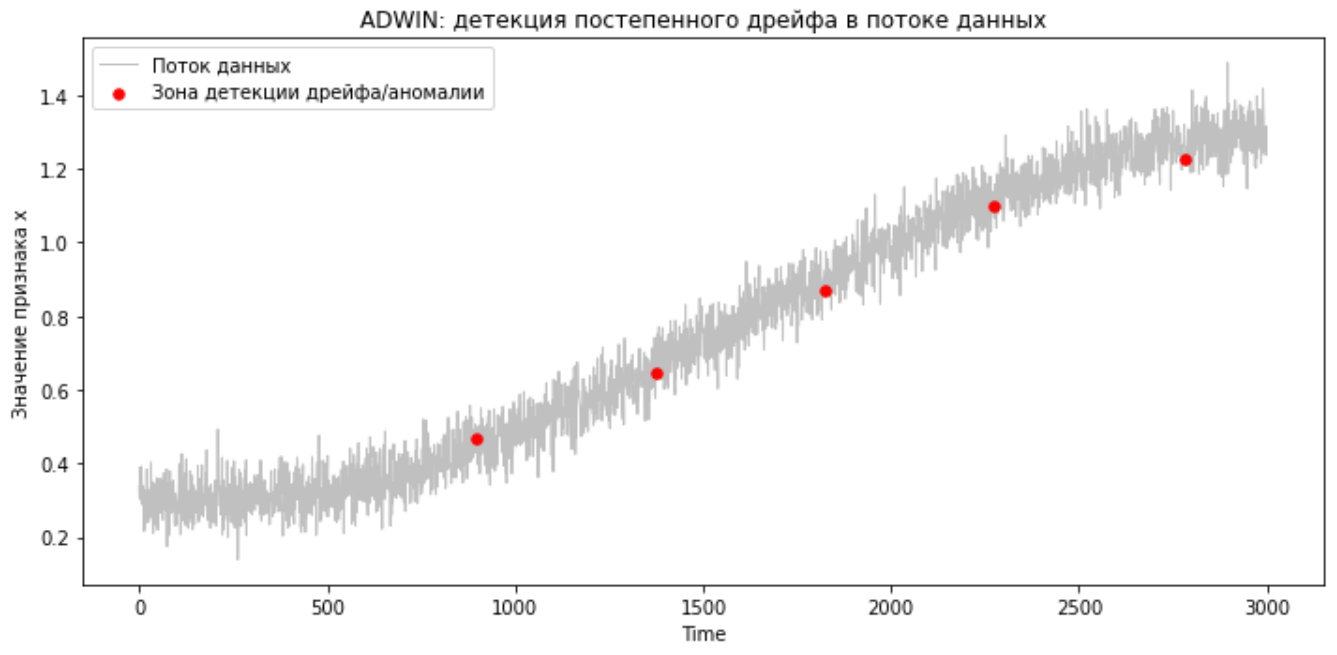
Здесь ADWIN также видит дрейф.
Drift Detection Method (DDM)
ссылка на статью, ссылка на документацию.
DDM может косвенно обнаружить дрейф концепции, поскольку он основан на анализе частоты ошибок модели, а не входящих признаков. Если алгоритм обнаруживает увеличение частоты ошибок, которое превышает расчётный порог, то происходит сигнализация о возможном дрейфе, однако, мы не можем наверняка узнать, являются ли выявленные изменения дрейфом концепции или дрейфом данных. Чтобы ответить на этот вопрос, следует проверить на предмет дрейфа данных признаки, которые модель получает на вход. Если они стабильны, тогда можно судить о том, что происходит именно дрейф концепции. Это замечание также справедливо для метода EDDM, о котором мы поговорим позже.
Поскольку DDM анализирует частоту ошибок отслеживаемой в проде модели, на вход он получают поток из нулей и единиц, где 1 – модель ошиблась, а 0 – ошибки нет.
Параметры:
min_num_instances: int (default=30)
Минимальное необходимое количество проанализированных образцов для сигнализации о дрейфе.
warning_level: float (default=2.0)
Порог для зоны предупреждения о дрейфе. Чем меньше, тем чувствительнее детекция дрейфа.
out_control_level: float (default=3.0)
Порог для зоны детекции дрейфа. Чем меньше, тем чувствительнее детекция дрейфа
На выходе получаем зону детекции дрейфа или зону предупреждения о возможном дрейфе.
Следует отметить, что в случае, когда мы анализируем модель классификации, получить бинарный поток ошибок модели не сложно, однако, для модели регрессии необходимо будет подбирать порог отсечения, чтобы преобразовать значение ошибки модели в 0 или 1.
Для визуализации работы модели используем Prequential error (предварительную ошибку). Предварительная ошибка, вычисленная в момент времени i, основана на накопленной сумме функции потерь между прогнозируемыми и наблюдаемыми значениями:
Если построить график Pe(i), где i, в нашем случае, – момент времени, то в начале будет виден значительный разброс, а потом график станет более гладким. Резкий дрейф виден в местах перегиба графика. Если же график гладкий, но возрастающий, то, скорее всего, происходит постепенный дрейф.
Детекция резкого дрейфа с помощью DDM
Код
from river.drift import DDM
# Создадим поток ошибок модели с резким дрейфом.
# Для этого сгенерируем 3 отрезка с данными
# со случайным биноминальным распределением и разными вероятностями ошибки.
error_predictions_1 = np.random.binomial(1, 0.2, 1000)
error_predictions_2 = np.random.binomial(1, 0.5, 1000)
error_predictions_3 = np.random.binomial(1, 0.9, 1000)
error_predictions_stream = np.concatenate((error_predictions_1, error_predictions_2,
error_predictions_3))
# Вычислим Prequential error для визулизации работы метода
cumsum_error = np.cumsum(error_predictions_stream)
prequential_error = []
for i in range(len(cumsum_error)):
prequential_error.append( 1/(i+1) * cumsum_error[i] )
# Используем DDM для обнаружения дрейфа
drift_index_ddm = stream_drift_detecton(error_predictions_stream, DDM())
# Визуализируем работу метода:
drift_values_ddm = np.array(prequential_error)[drift_index_ddm]
names_DDM_a = {'title': 'DDM: детекция резкого дрейфа в потоке данных',
'xlabel': 'Time',
'ylabel': 'Prequential error',
'label': 'Prequential error'}
final_chart_dots(prequential_error, drift_index_ddm, drift_values_ddm,
names_DDM_a, abrupt_drift=True)
Как видно, DDM выявил резкий дрейф, но с некоторой задержкой. Следующий метод, который мы рассмотрим, является модернизацией DDM, однако выявляет дрейф быстрее, но пока опробуем DDM для детекции постепенного дрейфа.
Детекция постепенного дрейфа с помощью DDM
Создадим поток ошибок модели с медленным дрейфом. Для этого сгенерируем данные со случайным биноминальным распределением, где через каждые 200 наблюдений вероятность ошибки увеличивается на 0.1.
Код
# Создадим поток ошибок модели с резким дрейфом.
# Для этого сгенерируем данные со случайным биноминальным распределением,
# где через каждые 200 наблюдений вероятность ошибки увеличивается на 0.1.
l=[]
for p in np.arange(0.1, 1.1, 0.1):
l.extend(np.random.binomial(1, p, 200))
error_predictions_slow = np.array(l)Используем DDM на потоке данных с резким дрейфом (код такой же, как в блоке с детекцией резкого дрейфа).

DDM также выявляет и постепенный дрейф.
Early Drift Detection Method (EDDM)
ссылка на статью, ссылка на документацию
Метод раннего обнаружения дрейфа, который, как и DDM, полагается на частоту ошибок, даёт хорошие результаты при медленных постепенных изменениях. Это происходит за счет того, что помимо частоты ошибок, EDDM дополнительно отслеживает среднее расстояние между двумя ошибками.
На вход EDDM, также, как и для DDM, подаётся поток ошибок отслеживаемой в проде модели, где 1 – модель ошиблась, а 0 – ошибки нет.
Параметры:
min_num_instances: int (default=30)
Минимальное необходимое количество проанализированных образцов для сигнализации о дрейфе.
warning_level: float (default=2.0)
Порог для зоны предупреждения о дрейфе. Чем меньше, тем чувствительнее детекция дрейфа.
out_control_level: float (default=3.0)
Порог для зоны детекции дрейфа. Чем меньше, тем чувствительнее детекция дрейфа
На выходе получаем зону детекции дрейфа или зону предупреждения о возможном дрейфе.
Детекция резкого дрейфа с помощью EDDM
Код аналогичен коду из раздела про DDM, только drift_detector будет EDDM(). Перейдём сразу к визуализации работы метода:

Детекция постепенного дрейфа с помощью EDDM

EDDM также хорошо справляется с медленным дрейфом и имеет большую чувствительность по сравнению с DDM.
Другие методы выявления дрейфа в потоке данных можно найти в библиотеке River.
Методы обнаружения дрейфа в накопленных данных
Статистические методы
Этот подход использует различные статистические показатели, которые определяют, отличаются ли распределения двух наборов данных.
Поскольку для этих методов не нужна метка истинности предсказания модели и они относительно быстрые, можно получить индикатор изменения признаков ещё до потенциального ухудшения показателей производительности модели.
Вот некоторые из популярных методов.
Kolmogorov-Smirnov Test или KS Test
Критерий KS — это непараметрический критерий равенства непрерывных/дискретных одномерных распределений вероятностей, который можно использовать для сравнения выборки с эталонным распределением вероятностей или для сравнения двух выборок.
Код
from scipy import stats
def ks_test(old_data, new_data, p_value=0.05):
test = stats.ks_2samp(old_data, new_data)
if test[1] < p_value:
print('Распределения двух наборов данных различны')
else:
print('В распределении обоих наборов данных нет изменений или сдвигов')
return test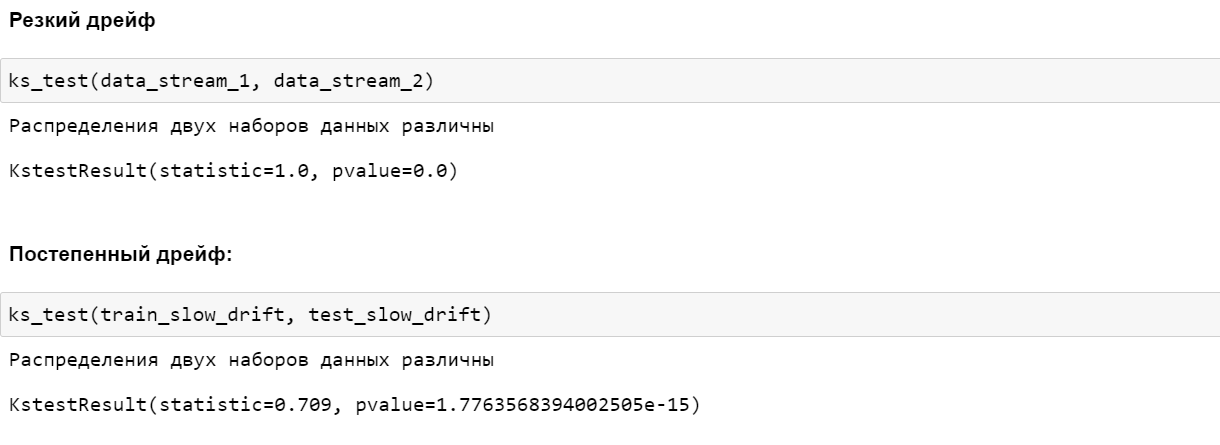
Population Stability Index
PSI является хорошей метрикой для оценки различия в распределении как для числовых, так и для категориальных признаков. Имейте в виду, что при расчёте данного индекса имеет значение порядок наборов данных, т.е. PSI наборов данных A и B не равен PSI B и A.
Шаги расчёта PSI:
сортируем старый набор данных по убыванию,
разделяем старый набор данных на бакеты (лучше на 10 или 20),
рассчитываем процент записей старого набора данных в каждом бакете (%Expected),
рассчитываем процент записей нового набора данных в каждом бакете (%Actual),
рассчитываем значение PSI по приведённой выше формуле,
-
bнтерпретируем результаты по следующей логике:
PSI <= 0,1: в распределении обоих наборов данных нет изменений или сдвигов,
0,1 < PSI < 0,2: небольшое изменение или сдвиг,
PSI > 0,2: между обоими наборами данных произошёл значительный сдвиг в распределении.
Код
def calculate_psi(old_data, new_data, buckets=10, axis=0):
# Разделяем старый набор данных на бакеты
breakpoints = np.arange(0, buckets + 1) / (buckets) * 100
breakpoints += -(np.min(breakpoints))
breakpoints /= np.max(breakpoints) / (np.max(old_data) - np.min(old_data))
breakpoints += np.min(old_data)
# Рассчитываем процент записей старого набора данных в каждом бакете
old_percents = np.histogram(old_data, breakpoints)[0] / len(old_data)
# Рассчитываем процент записей нового набора данных в каждом бакете
new_percents = np.histogram(new_data, breakpoints)[0] / len(new_data)
# Рассчитываем значение PSI
def sub_psi(old_perc, new_perc):
if new_perc == 0:
new_perc = 0.0001
if old_perc == 0:
old_perc = 0.0001
value = (old_perc - new_perc) * np.log(old_perc / new_perc)
return(value)
psi_value = np.sum(sub_psi(old_percents[i], new_percents[i])
for i in range(0, len(old_percents)))
# Интерпретируем результаты
if psi_value <= 0.1:
print('В распределении обоих наборов данных нет изменений или сдвигов')
elif psi_value > 0.2 :
print('Распределения двух наборов данных имеют значительные различия')
else:
print('В распределении наборов данных есть небольшое изменение или сдвиг')
return(psi_value)
Kullback-Leiber или KL Divergence
Дивергенция KL измеряет разницу между двумя распределениями вероятностей. Она также известна как относительная энтропия. Дивергенция KL полезна, если одно распределение имеет высокую дисперсию или небольшой размер выборки по сравнению с другим распределением. Оценка KL может варьироваться от 0 до бесконечности, где оценка 0 означает, что два распределения идентичны.
Jenson-Shannon или JS Divergence
Дивергенция JS — это ещё один способ количественной оценки разницы между двумя распределениями вероятностей. Она использует расхождение KL для расчёта нормализованной оценки, которая является симметричной. Это делает оценку расхождения JS более полезной и лёгкой для интерпретации, поскольку она обеспечивает оценки от 0 (идентичные распределения) до 1 (максимально разные распределения) при использовании логарифмической базы 2. С JS нет проблем с делением на ноль. Проблемы деления на ноль возникают, когда одно распределение имеет значения в регионах, которых нет в другом.
Wasserstein Metric или Earth Mover Distance
Это расстояние также известно как расстояние землеройной машины, поскольку его можно рассматривать как минимальный объём «работы», необходимой для преобразования одного распределения в другое, где «работа» измеряется как количество веса распределения, которое необходимо переместить, умноженное на расстояние, на которое его необходимо переместить.
Модельный подход
Adversarial validation
Этот подход включает в себя обучение модели классификации, помогающей определить, отличаются ли набор исторических данных от набора новых данных. Если модель с трудом различает данные, то существенного дрейфа нет. Если модель способна правильно разделить группы данных, то, вероятно, некоторый дрейф существует.
Adversarial validation по шагам:
исторические данные со всеми признаками помечаем таргетом 1, а новые данные - таргетом 0,
обучаем модель классификации отличать новые данные от исторических,
оцениваем работу модели (например, ROC-AUC),
если модель видит разницу, то предполагаем, что произошёл дрейф данных,
с помощью feature_importance можно посмотреть, за счёт каких признаков модель научилась различать старые данные от новых. Скорее всего в этих признаках произошёл сдвиг.
Обнаружение резкого дрейфа
Код
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import StratifiedKFold, cross_val_score
# Для демонстрации работы данного алгоритма создадим набор данных с двумя признаками:
# дрейфующим и стабильным:
data_stable_1 = random_state.normal(0.5, 0.05, 1000)
data_stable_2 = random_state.normal(0.5, 0.05, 1000)
df_old = pd.DataFrame({'feat1': data_stream_1, 'feat2': data_stable_1, 'target': 1})
df_new = pd.DataFrame({'feat1': data_stream_2, 'feat2': data_stable_2, 'target': 0})
df_abrupt_drift = pd.concat([df_old, df_new]).reset_index(drop=True)
# Обучим модель распознавать один набор данных от другого:
model = RandomForestClassifier(n_estimators=100, n_jobs=4, random_state=17)
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=17)
adv_validation_scores = cross_val_score(model,
df_abrupt_drift[['feat1', 'feat2']],
df_abrupt_drift['target'],
cv=skf,
n_jobs=4,
scoring='roc_auc')
model.fit( df_abrupt_drift[['feat1', 'feat2']], df_abrupt_drift['target'] )После обучения модели классификации, проверим оценку ROC-AUC и отобразим важность признаков в работе данной модели:

Модель видит различия в этих двух наборах данных именно за счёт признака с дрейфующими данными.
Обнаружение постепенного дрейфа:
Код
# Для демонстрации работы данного алгоритма создадим набор данных с двумя признаками:
# дрейфующим и стабильным:
df_old = pd.DataFrame({'feat1': data_stream_slow_drift[:1000], 'feat2': data_stable_1, 'target': 1})
df_new = pd.DataFrame({'feat1': data_stream_slow_drift[1000:2000], 'feat2': data_stable_2, 'target': 0})
df_slow_drift = pd.concat([df_old, df_new]).reset_index(drop=True)
# Обучим модель распознавать один набор данных от другого
model = RandomForestClassifier(n_estimators=100, n_jobs=4, random_state=17)
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=17)
adv_validation_scores_slow = cross_val_score(model, df_slow_drift[['feat1', 'feat2']],
df_slow_drift['target'], cv=skf, n_jobs=4,
scoring='roc_auc')
model.fit(df_slow_drift[['feat1', 'feat2']], df_slow_drift['target'])После обучения модели классификации, проверим оценку ROC-AUC и отобразим важность признаков в работе данной модели:

Здесь модель также видит различия в этих двух наборах данных именно за счёт признака с дрейфующими данными.
Недостатком этого подхода является то, что каждый раз, когда становятся доступны новые входные данные, необходимо повторять процесс обучения, что может быть дорогостоящим и трудозатратным.
Isolation Forest
Одним из простейших модельных методов обнаружения дрейфа данных является использование алгоритмов поиска аномалий. Часто в качестве базового алгоритма в подобных задачах применяется Isolation Forest. Рассмотрим его подробнее.
IsolationForest – алгоритм обучения без учителя. Он построен на деревьях и использует предположение о том, что объекты-выбросы достаточно сильно отличаются по своей структуре от стандартных объектов в выборке, следовательно, для их поиска требуется меньше информации.
Такие объекты находятся ближе к корням полученных деревьев. Чем ближе в среднем объект к корню, тем более аномальным он считается.
Данный алгоритм является достаточно чувствительным к шуму, поэтому прямое его использование на потоке данных часто даёт результаты хуже, чем у классических алгоритмов, однако данный алгоритм можно адаптировать под задачу выявления дрейфа, если собирать агрегированные статистики.
Хорошей практикой является обучение IsolationForest на плавающем окне за прошедшие N дней. Данный подход нацелен прежде всего на детекцию дрейфа, который происходит резко, скачкообразно. Он хорошо зарекомендовал себя на практике, поскольку позволяет сгладить естественную дисперсию в данных, но при этом по-прежнему имеет достаточно высокую чувствительность. Метод с использованием окна показал лучшие результаты в экспериментах с модельными данными.
Код
from sklearn.ensemble import IsolationForest
from sklearn.preprocessing import MinMaxScaler
# Изменение размерности потока данных
ds_abr = data_stream_abrupt_drift.reshape([-1,1])
# Подсчет агрегированных показателей:
n_agg = 20
data = ds_abr
mean_agg = []
std_agg = []
max_agg = []
min_agg = []
agg_25 = []
agg_50 = []
agg_75 = []
i1 = 0
i2 = i1 + n_agg
while i2 < len(data):
mean_agg.append( data[i1:i2].mean() )
std_agg.append( data[i1:i2].std() )
min_agg.append( data[i1:i2].min() )
max_agg.append( data[i1:i2].max() )
agg_25.append( np.quantile(data[i1:i2], 0.25) )
agg_50.append( np.quantile(data[i1:i2], 0.5) )
agg_75.append( np.quantile(data[i1:i2], 0.75) )
i1 = i2
i2 = i1 + n_agg
arr = [mean_agg, std_agg, min_agg, max_agg, agg_25, agg_50, agg_75]
data_agg = np.array(arr).T
# Обучение модели IsolationForest на плавающем окне
pred_data_agg = []
window_size = 30
for i in range( len(data_agg) - window_size ):
# Обучаем модель на предыдущем окне
model = IsolationForest(random_state=0).fit(data_agg[i: i + window_size])
# Делаем предсказания для текущего наблюдения
preds = list(model.decision_function(data_agg[i + window_size].reshape([1, -1])))
pred_data_agg = pred_data_agg + preds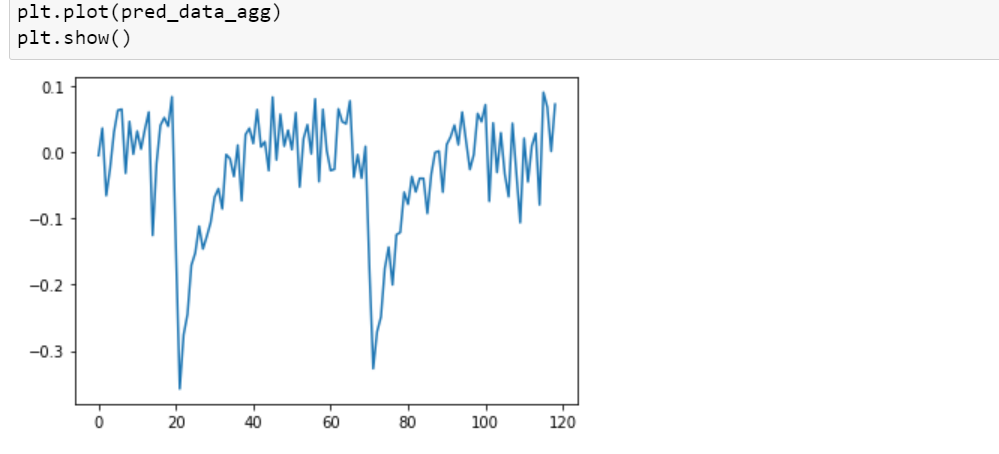
# Обозначим порог отсечения зоны аномалии так,
# чтобы оставить 5 точек с наибольшей (а фактически наименьшей) оценкой аномалии
threshold = np.quantile(pred_data, q = 5/len(pred_data_agg))
# оставим только значения оценки аномалии, запишем их в volume
vol = np.array([0 if pred >= threshold else pred for pred in pred_data_agg])
volume = -vol[vol<0].reshape(-1, 1)
# Индексы дрейфа
outlier_index = where(vol<0)
# Трансформируем индексы таким образом,
# чтобы можно было показать дрейф на полном потоке данных,
# а не на агрегированных/сдвинутых показателях данного потока
index_calculation = lambda t: (t + window_size + 1) * n_agg
outlier_index_full = [index_calculation(x) for x in outlier_index][0]
# Значения точки данных, где выявлен дрейф (значение оси y на нашем графике)
values = ds_abr[outlier_index_full].reshape(1, -1)[0]
# Для того, чтобы сделать отобразить на графике точки дрейфа
# с разной прозрачностью и размером в зависимости от оценки аномалии,
# трансформируем значения оценки аномалии посредством MinMaxScaler
scaler = MinMaxScaler(feature_range=(min(volume), 1))
scaler = scaler.fit(volume)
normalized_volume = scaler.transform(volume)
# Визуализация работы метода
fig = plt.figure(figsize=(10,5), tight_layout=True)
plt.title('Isolation Forest с плавающим окном на агрегированных статистических показателях потока данных')
plt.xlabel('Time')
plt.ylabel('Значение признака x')
plt.plot(ds_abr, label='Поток данных', color='silver', linewidth=1)
for index, x in enumerate(outlier_index_full):
plt.scatter(x = x, y = values[index], c = 'red', alpha = normalized_volume[index], s=normalized_volume[index]*100, zorder=2,
label='Зона фактического дрейфа' if index == 0 else None)
plt.vlines(drift_index_fact, ymin=min(ds_abr), ymax=max(ds_abr),
colors='black', linestyles='dashed', lw=2, zorder=5, label='Зона фактического дрейфа')
plt.legend()
plt.show()
Как видно, данный алгоритм хорошо справляется с выявлением резкого дрейфа.
Опыт практического использования Isolation Forest в Feature Store
Отслеживание дрейфа данных является одним из важнейших функционалов Feature Store, о котором мы говорили в одной из прошлых статей. Он позволяет своевременно реагировать на проблемы с фичами, вовремя принимать решение о необходимости переобучения моделей.
На одном из проектов перед нами стояла задача оценки качества фичей клиентского профиля, собираемого у заказчика. Необходимо было найти нестабильные, дрейфующие фичи, провести анализ возможных причин дрейфа.
Для её решения мы придумали простой, но в то же время эффективный алгоритм, использующий Isolation Forest, который позволил на регулярной основе собирать, накапливать и анализировать данные по стабильности фичей. Данная статистика позволила нам отыскать фичи, в которых наиболее вероятно произошёл дрейф, что значительно сократило объем требуемого ручного анализа.
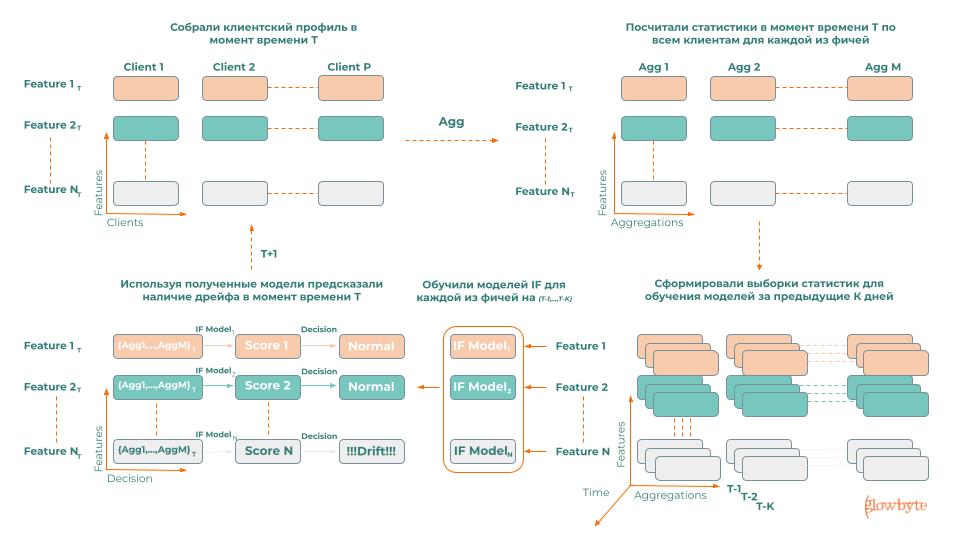
Расскажем про него подробнее:
для каждого из имеющихся признаков ежедневно собирали статистики по всей клиентской базе, такие как среднее, стандартное отклонение, квантили, заполненность и т. д., тем самым создавая его признаковое описание;
обучили Isolation Forest на статистиках за прошедшие N дней по данному признаку;
предсказали, произошёл ли дрейф данных в текущий день.
Немного о стратегии отслеживания дрейфа
Каждый из рассмотренных методов имеет свои плюсы и минусы, поэтому хорошей практикой является комплексный подход к детекции дрейфа: например, использовать ADWIN на важных признаках, DDM для отслеживания дрейфа концепции, статистические методы применять с определённой периодичностью для признаков в Feature store, в случае, если есть подозрение на комплексный дрейф, или для понимания, какие именно признаки дрейфуют, использовать Adversarial validation.
Косвенным признаком дрейфа концепции также может являться изменение состава наиболее важных признаков в модели. Например, если при обучении модель в своих предсказаниях использовала определённый состав признаков, а в последующем эти признаки перестали быть важными, значит, концепция поменялась.
Стратегия отслеживания дрейфа подбирается с учётом особенностей проекта.
Что делать с выявленным дрейфом
Существуют разные подходы к реакции на дрейф данных, но начать следует с анализа первопричины.
Варианты реагирования на выявленный дрейф
1. Откалибруйте или перестройте модель
Удалите или скорректируйте дрейфующие признаки, сохраните модель. Один из вариантов работы с дрейфующими признаками, состоит в том, чтобы просто удалить их из рассмотрения моделью или обработать, например, заменить их средним значением. Это не требует сбора дополнительных размеченных данных или переобучения, но может привести к некоторой потере производительности. Однако, если эти потери ниже, чем ожидаемая деградация из-за дрейфа, удаление может быть хорошим вариантом.
Удалите или скорректируйте дрейфующие признаки, переобучите модель. В некоторых случаях можно удалить дрейфующий признак и надеяться, что переобучение использует альтернативные признаки для достижения аналогичной прогностической способности.
Обновите модель. Переобучите модель на новых данных.
Обучите модель на взвешенных данных. Вместо того, чтобы отбрасывать старые данные, используйте вес, обратно пропорциональный давности данных.
Измените цель предсказания. Например, переключитесь с еженедельного на ежедневный прогноз или замените регрессионную модель моделью классификации с разбиением по категориям от «высокого» к «низкому».
2. Рассмотрите решение, не связанное с ML. Например, примените поверх модели бизнес-логику, основанную на понимании причинно-следственных связей, сути процесса или экспертных знаний.
3. Ничего не делайте и продолжайте использовать ту же обученную модель. В большинстве случаев это будет наивный подход, однако он может быть рассмотрен в качестве варианта по нескольким причинам:
изменение качества работы модели может находиться в допустимых границах;
вы получите время на сбор меток и возможность принять более взвешенное решение;
обнаруженный дрейф может быть временным.
Анализ первопричины дрейфа может привести к значительно более точным стратегиям смягчения его последствий.
Все перечисленные методы и инструменты могут помочь куда легче перенести происходящие изменения.
Про дрейф, Feature Store и другие вопросы вокруг применения ML и продвинутой аналитики в реальных бизнес-задачах мы регулярно общаемся в нашем сообществе NoML:
Также приглашаем посмотреть запись нашего доклада на базе данной статьи.
Над статьёй работали: @Anna-Mur , @AVKosov, @vagonoff , @Lazarev_Adrian.
Ссылка на гит: https://github.com/Anna-Mur/Data_drift_detection

