В этой статье подробно разбирается алгоритм обучения архитектуры CBOW (Continuous Bag of Words), которая появилась в 2013 году и дала сильный толчок в решении задачи векторного представления слов, т.к. в первый раз на практике использовался подход на основе нейронных сетей. Архитектура CBOW не столь требовательна к наличию GPU и вполне может обучаться на ЦП (хотя и более медленно). Большие готовые модели, обученные на википедии или новостных сводках, вполне могут работать на 4-х ядерном процессоре, показывая приемлемое время отклика.

Архитектура CBOW

CBOW архитектура была предложена группой исследователей из компании Google в 2013 году совместно с Skip-gram моделью. Логика CBOW архитектуры очень проста: предсказать слово в зависимости от контекста, в котором находится это слово. Пример архитектуры нейронной сети в самом простом варианте реализации CBOW при использовании всего одного слова (контекста) перед целевым словом приведен на рисунке 1. В дальнейшем в статье мы перейдем от простой модели на основе одного слова к большему контексту.

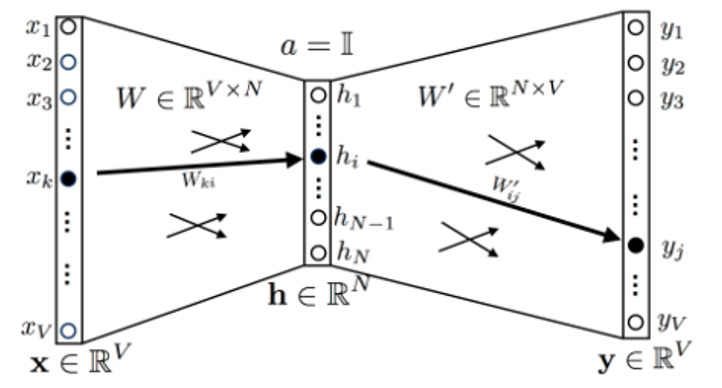
Архитектура нейронной сети состоит из одного слоя размерности  корпуса текста, иначе говоря, длина словаря. Скрытый слой имеет размерность N. Выходной слой имеет такую же размерность, как и входной слой. Функция активации скрытого слоя является линейной, а в выходном слое – обобщенной логистической функцией активации:

Матрица весов между входным слоем и скрытым обозначена буквой W и имеет размерность V x N. Веса между скрытым слоем и выходным обозначим W', они будут иметь размерность N x V. Стоит отметить, что перед обучением необходимо векторизовать слова. Сделать это можно с помощью простого унитарного кода или, например, статистической меры TFIDF.

Рассмотрим, как будет рассчитываться выходное значение, исходя из архитектуры, представленной на рисунке 1. Вначале веса инициализируются с помощью стандартного нормального распределения. Затем рассчитываются значения в скрытом слое по формуле:

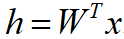
Точно так же рассчитываются значения после прохождения скрытого слоя, но до попадания в функцию активации выходного слоя.

Выбор функции потерь для оценки выходного слоя нейронной сети основывается на получении диапазона значений в промежутке от 0 до 1. При этом, учитывая, что на выходе мы имеем логистическую функцию активации, которую в данной задаче можно интерпретировать как условную вероятность появления слова после определенного контекста, функцию потерь мы можем задать следующим образом:

где  w_t – целевое слово,  w_c – контекстное слово.

Немного преобразовав, можно получить более простую запись:

Для решения поставленной задачи нам требуется минимизировать данную функцию потерь и максимизировать вероятность того, что модель предсказывает целевое слово с учетом контекста (на данном этапе состоящего из одного слова).

Обучение CBOW при одном слове в контексте

Получив выражение функции потерь, необходимо найти минимизирующие её значения W и W'. Проблема оптимизации нейронных сетей чаще всего решается с помощью градиентного спуска. Для того чтобы реализовать алгоритм обратного распространения ошибки, основанный на градиентном спуске, необходимо найти частные производные

Проще всего установить взаимосвязь между W, W' и функцией потерь через вектор

то есть можно записать следующее соотношение:

Таким образом, для частных производных будет справедливо:

Этих соотношений достаточно для обучения CBOW архитектуры.

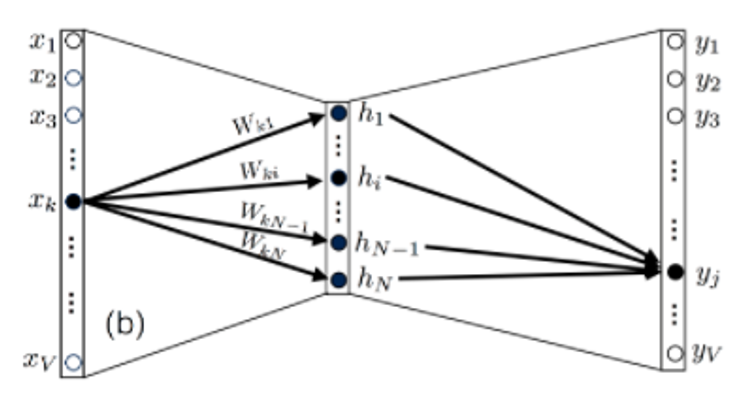
Рассмотрим возможности упрощения модели. Заметим, что вес W’_ij, который является элементом W’, соединяет узел i скрытого слоя с узлом j выходного слоя. То есть W’_ij влияет только на оценку u_j (а также y_j) как показано на рисунке 2. Это происходит из-за того, что в упрошенной модели (при использовании одного слова в контексте) вектор x, подающийся на вход нейронной сети, будет содержать нули с x₀ до x_V включительно за исключением точки x_k, где будет стоять единица. То есть после прохождения функции активации все веса W’_ij за исключением h_j, будут равны 0. Данное предположение справедливо в случае использования векторизации на основе унитарного кода.

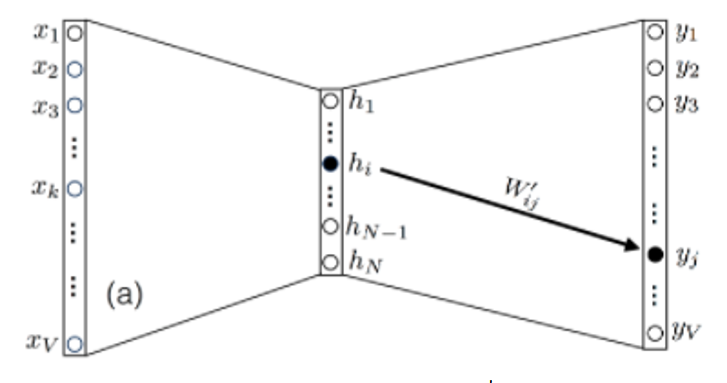
Исходя из вышесказанного, можно предположить, что частная производная

 равна нулю везде, кроме k = j. Тогда можно переписать производную следующим образом:

Преобразуем теперь

как

где

– дельта Кронекера – функция от 2 переменных, которая равна 1, когда , а в остальных случаях равна 0. Для второй части уравнения мы имеем:

Тогда после объединения левой и правой части получаем:

Аналогично можно выполнить те же операции для производной

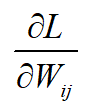
однако стоит отметить, что после фиксации входа x_k выход в узле j будет зависеть от всех элементов матрицы W, как показано на рисунке 3.

Перед тем как преобразовать

можно отдельно выписать u_k из вектора u:

Из этого уравнения легко можно выписать производную

так как единственный член, который останется после действия суммы, будет тот, в котором l = i и m = j. Таким образом,

Собирая все воедино, получаем:

Проведя все преобразования, мы получили все необходимые соотношения для реализации первого «обучающего» прохода для алгоритма градиентного спуска. Для того чтобы применить алгоритм градиентного спуска, необходимо теперь выбрать скорость обучения

В общем случае скорость обучения является гиперпараметром к любой модели машинного обучения или нейронных сетей. С выбором параметра могут возникнуть трудности, а именно: при выборе большого параметра алгоритм может перепрыгнуть точку минимума функции или вообще «застрять», прыгая из стороны в сторону, но так и не достигнув минимума. В случае же более низких значений скорость обучения будет очень медленной. Однако стоит отметить, что в данном случае пропустить точку минимума очень трудно. Рекомендуется использовать коэффициент в диапазоне

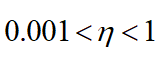
Обновление весов W и W' происходит по следующей формуле:

Одного шага для нахождения минимума даже такой простой архитектуры, как CBOW, недостаточно. Поэтому при обучении нейронных сетей имеется еще один важный параметр, а именно количество эпох.

Эпоха – один полный цикл обучения, то есть прохождение всех обучающих примеров ровно 1 раз. Выбор количества эпох зависит только от исследователя и от того, сколько он намерен ждать, пока его сеть обучится. При наличии возможности выбора большого количества эпох коэффициент обучения выбирается близким к нулю.

Обучение CBOW в общем виде

Зная, как работает алгоритм обучения на основе обратного распространения ошибки при одном слове в контексте, мы можем ввести дополнительную сложность, включив больше контекстных слов, как показано на рисунке 4. При этом стоит отметить, что мы можем рассматривать слова не только позади целевого слова, но и впереди, то есть в контексте.

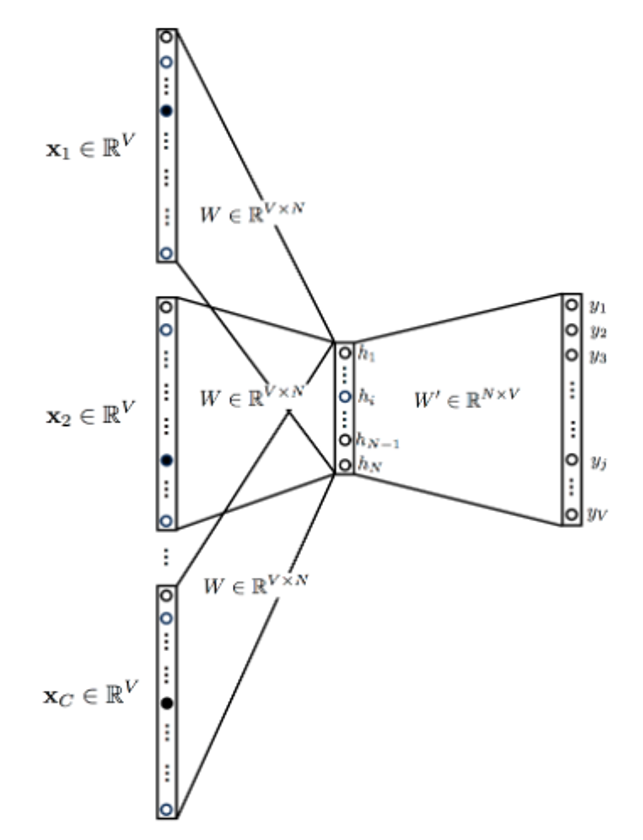
Входные данные представляют собой контекстные слова, закодированные унитарно. Количество контекстных слов C зависит от нашего выбора (сколько контекстных слов мы хотим использовать). Скрытый слой становится средним значением, полученным из каждого контекстного слова.

Общая архитектура CBOW имеет те же уравнения, что и архитектура из одного слова, но только обобщенная на случай использования произвольного количества контекстных слов C:

Функция активации выглядит точно так же, как и при использовании одно слова в контексте:

Производные функции потерь вычисляются так же, как и при использовании одного слова в контексте, за исключением того, что входной вектор

заменяется на среднее по входному вектору

Как видно, общая архитектура и процесс обучения легко могут быть выведены из простой модели, использующей всего  одно слово в контексте.

Алгоритм векторизации текста на основе CBOW архитектуры может применяться и в современных системах, потому что в отличии от BERTa и ELMo обладает более высокой скоростью работы при использовании CPU. Особенно часто такие реализации можно встретить у клиентов, не обладающих достаточными вычислительными мощностями. Более подробно об одном таком случае вы можете прочитать в нашей следующей статье.