Продолжаем серию статей, посвящённых методам множественного доступа в беспроводной связи. В первой части мы рассмотрели методы разделения пользователей по частоте, по времени и с комбинированным частотно-временным разделением. Во второй части – неортогональные методы разделения по мощности и их комбинации с другими методами.
В третьей части мы рассмотрим методы множественного доступа с разделением пользователей в ещё одном ресурсном пространстве – кодовом. Среди них будут встречаться как ортогональные методы (CDMA, LAS-CDMA), так и неортогональные (LDS-CDMA, SCMA, SAMA, MUSA, NCMA, NOCA, GOCA, IDMA, IGMA, RDMA, RSMA). Также рассмотрим особую разновидность кодового разделения – битовое разделение (методы BDM, CEMA, REMA, EDC-NOMA, M-NOMA, BOMA). Как обычно, обсудим основные преимущества и недостатки всех этих методов.

Множественный доступ с ортогональным кодовым разделением (CDMA)
Начнём с хорошо известного и популярного метода множественного доступа, используемого в современных системах связи, например, в стандарте сотовой связи 3G. Речь пойдёт о множественном доступе с кодовым разделением (code division multiple access, CDMA). В системах CDMA радиоканалы используют одни и те же частотно-временные ресурсы. Сигналы, принадлежащие отдельным пользователям, разделяются за счёт того, что сигналу каждого пользователя назначается своя адресная кодовая последовательность.
В технологии кодового разделения каналов используется передача широкополосных сигналов. Широкополосные сигналы обычно представляют собой сигналы с фазовой манипуляцией, полученные на базе кодовых последовательностей с хорошими корреляционными свойствами.
Существуют три основных метода расширения спектра сигналов:
Скачкообразная перестройка несущей частоты (frequency hopping, FH-CDMA). Системы FH-CDMA обладают высокой помехозащищённостью и низкой вероятностью перехвата. Любой бит передаётся с помощью набора из N дискретных частот в виде частотно-временной матрицы, причём на каждой частоте передаётся своя кодовая последовательность. В течение определённого интервала времени T несущая остаётся постоянной, а по его окончании она скачкообразно изменяется. Алгоритм переключения частоты несущей для каждого абонента индивидуален, благодаря этому в общей полосе частот может одновременно работать большое число абонентов.
Псевдослучайная перестройка во времени (time hopping, TH-CDMA). В методе TH-CDMA информационный сигнал передаётся в виде коротких пакетов в случайные моменты времени, определяемые специальной кодовой последовательностью. Временная ось при использовании TH-CDMA разбивается на кадры длительностью T, каждый из которых состоит из M временных интервалов длительностью T/M. В течение одного кадра информация передаётся только в одном из временных интервалов.
Прямое расширение спектра (direct sequence, DS-CDMA). Именно эта технология применяется в системах сотовой связи, в дальнейшем будем называть её просто CDMA. Здесь исходный узкополосный сигнал умножается на расширяющую кодовую последовательность, состоящую из N элементов длительностью Δ каждый и имеющую период повторения T = NΔ. Обычно используют бинарные кодовые последовательности, состоящие из элементов, которые условно можно обозначить +1 и –1. При этом единичный бит информационных данных инвертирует кодовую последовательность, а нулевой бит оставляет её неизменной.
В системах сотовой связи CDMA используется прямое расширение спектра на основе 64 ортогональных кодовых последовательностей, сформированных с помощью функций Уолша. Функции Уолша – это строки матрицы Адамара, которая определяется следующим образом:
Исходной матрицей является матрица
Подставляя её в предыдущее выражение, получим новую матрицу второго порядка:
Многократно повторяя эту процедуру, мы можем сформировать матрицу любого размера, у которой все строки и столбцы ортогональны.
Однако ортогональным кодам присущи два главных недостатка:
Максимальное число возможных кодов ограничено их длиной, и, значит, они имеют ограниченное адресное пространство. Например, в стандарте IS-95 число кодов равно 64. Для расширения ансамбля сигналов наряду с ортогональными используются квазиортогональные последовательности. С помощью m специальных маскирующих функций и ансамбля кодов Уолша длиной 2n можно создать квазиортогональных последовательностей.
Для ортогональных кодов взаимная корреляционная функция равна нулю лишь “в точке”, т.е. при отсутствии временного сдвига между кодами. Поэтому такие сигналы используются лишь в синхронных системах и преимущественно в нисходящих каналах (от базовой станции к абоненту).
Система CDMA может адаптироваться к различным скоростям передачи за счёт использования специальных ортогональных последовательностей с переменным коэффициентом расширения спектра (orthogonal variable spreading factor, OVSF), называемых кодами переменной длины. При передаче сигнала CDMA, сформированного с помощью такой последовательности, чиповая скорость остаётся постоянной, а информационная скорость изменяется кратно двум. Ансамбль OVSF кодов не является фиксированным: он зависит от коэффициента расширения спектра, т.е. фактически от скорости канала.
Кроме ортогональных кодов, в системах CDMA также используются псевдослучайные последовательности (ПСП). Это детерминированные периодические сигналы, известные передатчику и приёмнику. Для “неуполномоченного” пользователя такой сигнал будет неотличим от белого шума. ПСП выгодно отличаются от ортогональных последовательностей инвариантностью к временному сдвигу. В качестве ПСП могут выбираться M-последовательности, а также построенные на их основе коды Голда, коды Касами и т.д.
Скажем пару слов о приёме сигналов в системе CDMA. Сигнал, модулированный кодовой последовательностью при передаче, повторно модулируется той же последовательностью при приёме, в результате чего восстанавливается исходный сигнал. Подбор задержки демодулирующей последовательности производится с точностью до дискрета последовательности, и правильному значению задержки соответствует максимальный отклик на выходе фильтра-демодулятора. Такая схема обработки называется корреляционным приёмом.
Множественный доступ с использованием LAS-кодов (LAS-CDMA)
Перейдём теперь к некоторым модификациям технологии CDMA. Но сначала надо понять, что не так с традиционным методом CDMA и для чего понадобилось его модифицировать. Дело в том, что в CDMA и автокорреляционные функции, и взаимные корреляционные функции неидеальны, т.е. в CDMA сигналы различных пользователей подвержены взаимной интерференции.
Давайте посмотрим на рис. 1, где приведён пример автокорреляционной и взаимной корреляционной функции для кодовых последовательностей, используемых в традиционных системах CDMA. Мы видим, что, во-первых, боковые лепестки обеих этих функций равны нулю далеко не везде. Во вторых, требования сохранения на низком уровне боковых лепестков как одной, так и другой функции противоречат друг другу. При разработке традиционных систем CDMA достигается некоторый компромисс: обычно боковые лепестки автокорреляционной и взаимной корреляционной функций устанавливаются на уровне около , где B – база сигнала (напомним, что база сигнала – это произведение его длительности на эффективную ширину спектра). Эта нижняя граница называется границей Уэлча. Таким образом, взаимная интерференция, наведённая пользователями, не может быть полностью устранена, и традиционные системы CDMA ограничены этой интерференцией.
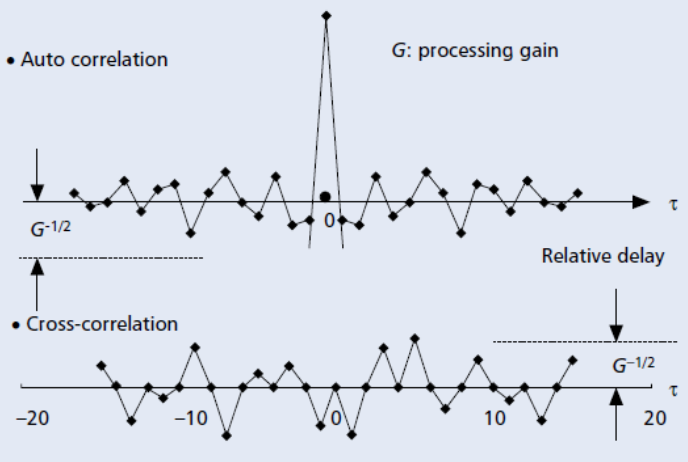
Для устранения этого недостатка была предложена новая схема множественного доступа – синхронизированный на большой площади множественный доступ с кодовым разделением (large area synchronized code division multiple access, LAS-CDMA). Автокорреляционные функции всех кодов в системе LAS-CDMA идеальны, а на их взаимных корреляционных функциях существует окно без корреляции (interference-free window, IFW), симметричное относительно нуля. Благодаря наличию IFW, система LAS-CDMA может иметь намного более высокую ёмкость и спектральную эффективность, чем традиционная технология CDMA.
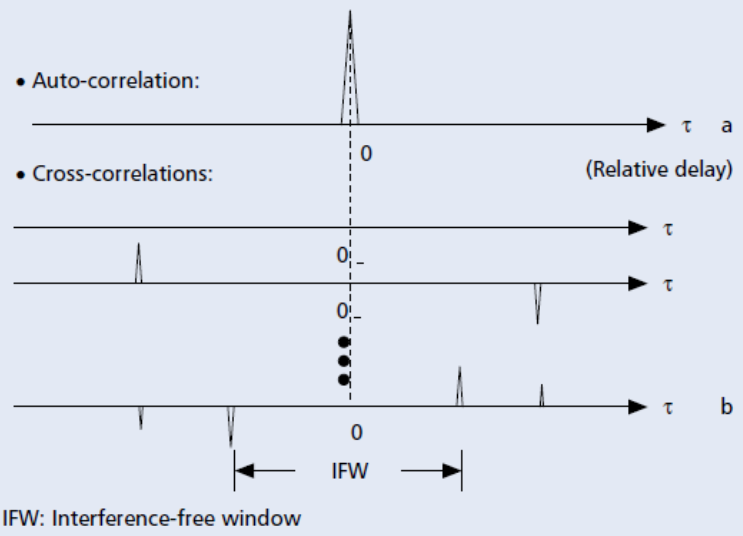
В схеме LAS-CDMA используются два семейства CDMA кодов – LA-коды и LS-коды. LA-коды – семейство последовательностей импульсов с точно рассчитанными интервалами между импульсами. LA-коды в основном используются для уменьшения интерференции между соседними сотами. Импульсы LA-кодов формируются путём прохождения LS-кода через его согласованный фильтр на нужных позициях импульсов. LS-коды используются для расширения спектра. Семейство LS-кодов обладает интересными корреляционными свойствами. На рис. 2, а приведён пример идеальной автокорреляционной функции LS-кодов. Некоторые взаимные корреляционные функции также идеальны, но большинство из них имеют лишь несколько пар боковых лепестков (рис. 2, b). Видно, что на взаимных корреляционных функциях существуют области, в которых боковые лепестки отсутствуют. Такие области вокруг нуля и называются IFW.
Преимущество синхронизированных систем LAS-CDMA состоит в том, что если временная дисперсия (возникающая из-за многолучевого распространения) канала находится внутри такого IFW, то и межсимвольная интерференция, и межпользовательская интерференция практически будут отсутствовать.
Множественный доступ с кодовым разделением с расширяющими кодами низкой плотности (LDS-CDMA)
Теперь мы переходим к рассмотрению большой группы неортогональных методов множественного доступа с кодовым разделением. В целом они подобны традиционному CDMA. Отличие заключается в том, что сигналы отдельных пользователей не являются ортогональными друг другу. Первый из методов этой группы – множественный доступ с кодовым разделением с расширяющими кодами низкой плотности (low density spreading code division multiple access, LDS-CDMA) основан на использовании сигнатур с низкой плотностью (low-density signature, LDS).
В LDS-CDMA сигнал формируется следующим образом: символы квадратурной амплитудной модуляции умножаются на комплексную расширяющую последовательность (или, как говорят, сигнатуру). Часть элементов сигнатуры являются нулевыми, поэтому такие сигнатуры называются разреженными.
На приёмной стороне суммарный сигнал от всех пользователей поступает на вход многопользовательского детектора, который декодирует принятый сигнал. В многопользовательском алгоритме приёма минимизируется квадрат евклидова расстояния между принятым сигналом и суммарным сигналом от всех пользователей. Данный алгоритм формирует оценки по правилу максимального правдоподобия. На практике часто применяются субоптимальные алгоритмы, в частности, итерационный алгоритм обмена сообщениями (message passing algorithm, MPA). Этот алгоритм обладает умеренной вычислительной сложностью и обеспечивает помехоустойчивость, близкую к алгоритму максимального правдоподобия.
На рис. 3 приведён пример схемы LDS-CDMA с 6 пользователями.
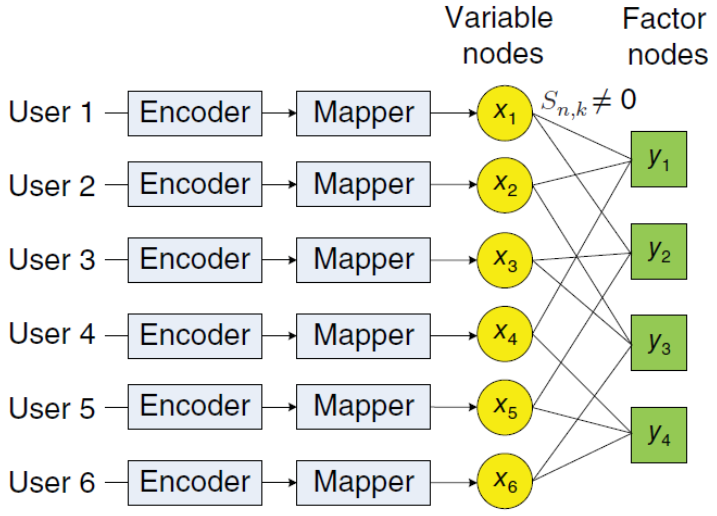
Модификацией этой технологии является технология LDS-OFDM. Она имеет свойства, аналогичные LDS-CDMA. Отличие заключается в том, что выходные данные отображаются на поднесущие OFDM, а не на временные выборки в CDMA. Следовательно, можно использовать детектор MPA с низкой сложностью. Технология LDS-OFDM использует передачу с несколькими несущими, что делает её пригодным для широкополосных каналов. Кроме того, высокая совместимость с OFDM делает её гибкой в распределении частотно-временных ресурсов.
Множественный доступ с разреженным кодированием (SCMA)
Множественный доступ с разреженным кодированием (sparse code multiple access, SCMA) – это обобщение системы LDS-CDMA. В SCMA передача данных ведётся на ортогональных поднесущих, формируемых с помощью обратного быстрого преобразования Фурье (как в OFDMA). Метод SCMA разработан на основе LDPC-кодов с низкой плотностью проверок на чётность, в которых для распределения пользователей по поднесущим используются разреженные матрицы. Характеристики SCMA полностью определяются так называемыми кодовыми книгами, которые построены на формирующих разреженных матрицах. Каждый абонент передаёт биты bv, которые предварительно подверглись помехоустойчивому кодированию. Биты поступают на специальный кодер, который выполняет две функции. Во-первых, он выполняет распределение пользователей по поднесущим. Во-вторых, каждой группе битов пользователя он ставит в соответствие набор комплексных амплитуд, отображаемых на поднесущие (т.е. используется квадратурная амплитудная модуляция). При этом каждый пользователь ведёт передачу на нескольких поднесущих, т.е. применяется расширение спектра. Сформированные таким образом комплексные амплитуды поднесущих поступают на блок формирования сигнала во временной области, например, классический OFDM, включающий блок обратного быстрого преобразования Фурье и добавление циклического префикса.
Распределение пользователей по поднесущим проводится в соответствии с разреженной матрицей B. На рис. 4, а приведён пример такой матрицы, которую можно также представить в виде фактор-графа (рис. 4, б). Круги на графе (столбцы матрицы B) соответствует поднесущим, а квадраты на графе (строки матрицы B) соответствует пользователям. Рёбра графа, соединяющие вершины, показывают, на каких поднесущих ведёт передачу каждый пользователь. Индекс k соответствует поднесущим, индекс v – пользователям.
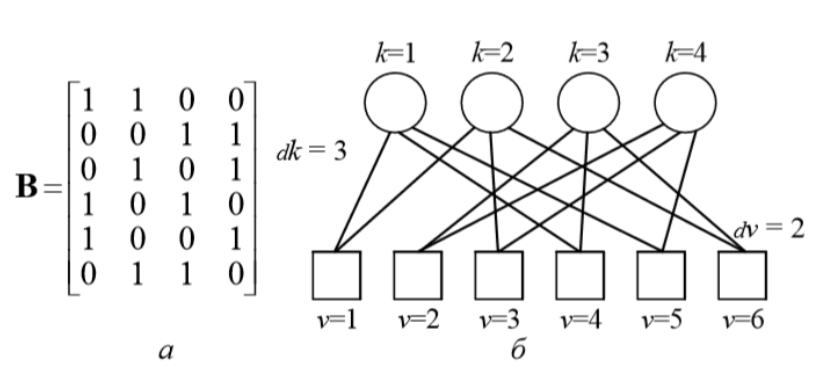
На основе разреженной матрицы строится кодовая книга SCMA, содержащая значения комплексных амплитуд, модулирующих поднесущие. На рис. 5 приведён пример такой кодовой книги для матрицы B, рассмотренной выше.
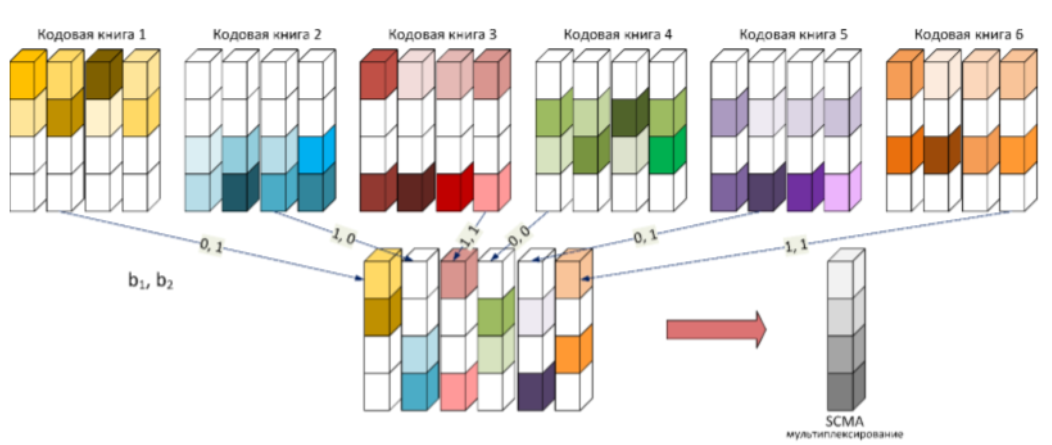
В зависимости от значения битов, передаваемых каждым пользователем, выбирается соответствующее им кодовое слово. Итоговый символ SCMA формируется как сумма всех V кодовых слов. На каждой поднесущей формируется результирующее сигнальное созвездие.
Детектирование символов в методе SCMA основано на уже знакомом нам алгоритме MPA. Он основан на пересчёте вероятностей двунаправленной передачи сообщений на фактор-графе в течение нескольких итераций.
Система SCMA считается одной из наиболее перспективных для использования в современных радиоинтерфейсах благодаря ряду преимуществ:
Системы множественного доступа, использующие кодовые книги на основе разреженных матриц, могут адаптивно подстраиваться под состояние канала;
Кодовые книги потенциально способны обеспечить меньшую вероятность битовых ошибок по сравнению с другими системами;
Не требуется передача служебной информации при организации восходящего канала, что улучшает спектральную эффективность системы;
Число пользователей может быть больше числа поднесущих, что позволяет обеспечить работу большего числа пользователей по сравнению с существующими системами связи;
SCMA превосходит существующие системы OFDM в помехоустойчивости.
У системы SCMA есть и ряд недостатков:
Необходимость использования нелинейного приёмника;
Сложность разработки кодовых книг. Для получения кодовых книг в SCMA используется субоптимальный алгоритм, в котором применяется множество допущений для снижения вычислительной сложности задачи. В отсутствие теоретических оценок пока непонятно, насколько получаемые результаты далеки от предельно достижимых.
Множественный доступ с последовательной компенсацией помех (SAMA)
Множественный доступ с последовательной компенсацией помех (successive interference cancellation amenable multiple access, SAMA) основан на использовании матрицы сигнатур и алгоритме MPA, разработанном на основе алгоритма последовательной компенсации помех (SIC). Схема SAMA может использоваться не только в кодовом ресурсном пространстве, но и в физическом пространстве, и во временной области.
Эта схема множественного доступа имеет следующие особенности:
Размер групп, которые имеют разное количество единиц в расширяющей последовательности, должен быть максимален;
Перекрытия расширяющих последовательностей пользователей, которые имеют одинаковое количество единиц, должно быть сведено к минимуму.
На основе приведённых выше требований максимальное число поддерживаемых пользователей для расширяющей матрицы системы с расширяющим фактором ???? (расширяющий фактор – это отношение чиповой скорости к символьной скорости) определяется выражением:
где
число сочетаний из ???? элементов по ???? элементов.
На основе этого выражения можно, например, разработать структуру SAMA для ???? = 3, ???? = 7 со следующей матрицей фактор-графа:
Фактор-граф, соответствующий этой матрице, приведён на рис. 6.
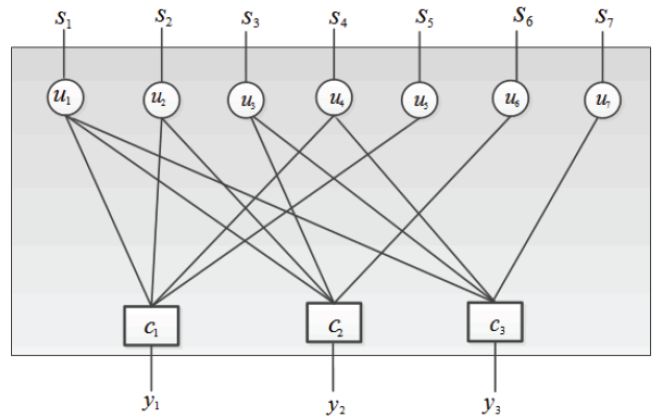
Позиции, на которых стоят единицы в i-й строке матрицы F, обозначают набор пользователей, которые вносят свои данные в чип с i-м номером, а j-й столбец матрицы представляет набор чипов, по которым пользователь распределяет свои данные. Т.к. матрицы имеют различное число нулей в каждом столбце, то эффективные расширяющие факторы (effective spreading factors, ESF) для различных пользователей различны. Для приведённой выше матрицы для пользователя 1 ESF равен 3, для пользователей 2, 3 и 4 ESF равен 2, и для пользователей 5, 6 и 7 он равен 1.
Множественный доступ с сигнатурами, основанными на комплексных кодовых последовательностях
Рассмотрим класс методов, в которых расширяющие последовательности выбираются из множества комплексных чисел. В первую очередь, к этому классу принадлежит система многопользовательского общего доступа (multi-user shared access, MUSA). Здесь сигнатуры представляют собой комплексные псевдослучайные последовательности, действительная и мнимая части которых обычно выбираются из множества {−1, 0, 1}.
На рис. 7 показано, как для 6 пользователей образуется суммарный сигнал, который затем декодируется методом последовательной компенсации помех (SIC), подобно системе PD-NOMA (см. Часть 2). В приведённом примере длина кодового слова равна 4. Каждый элемент кодового слова может принимать одно из 9 комплексных значений, которые обозначены различными цветами. Кодовая книга содержит n специально выбранных кодовых слов. Каждый пользователь может случайным образом выбирать кодовое слово для расширения своего символа данных.
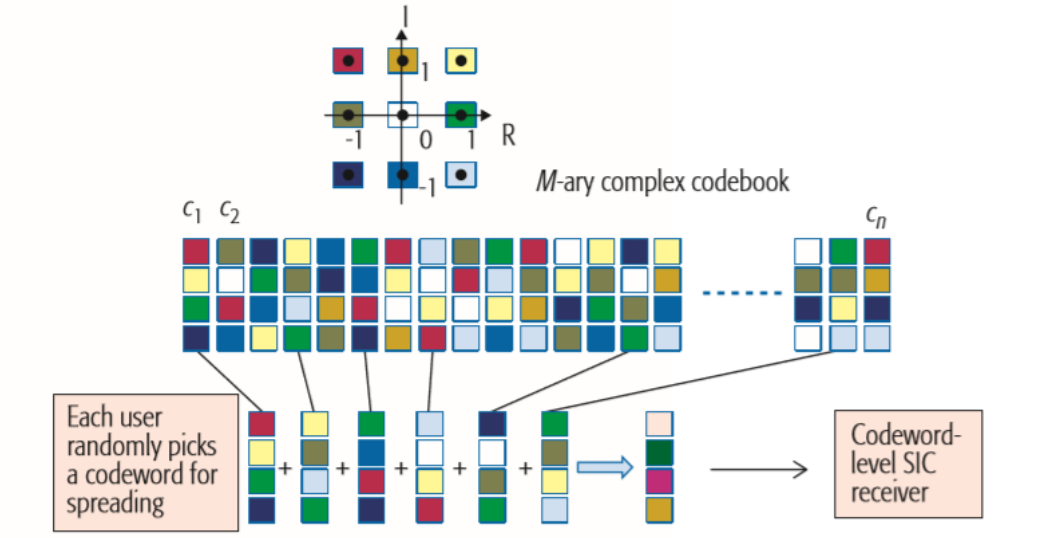
Для обеспечения лучшей помехоустойчивости применяется декодирование методом SIC совместно с приёмником, минимизирующим средний квадрат ошибки (minimum mean square error, MMSE).
К этому же классу относятся ещё 3 метода: неортогональный кодированный множественный доступ (non-orthogonal coded multiple access, NCMA), неортогональный кодированный доступ (non-orthogonal coded access, NOCA) и групповой ортогональный кодированный доступ (group orthogonal coded access, GOCA), предложенные для использования в стандартах 5G. Несмотря на то, что в названии GOCA содержится слово “ортогональный”, в этой системе используются как ортогональные, так и неортогональные комплексные сигнатуры, которые в общем случае могут выбираться из произвольного комплексного алфавита. Здесь неортогональные последовательности применяются для разделения групп, а ортогональные – для разделения пользователей внутри группы. В этих системах сигналы декодируются методом SIC в сочетании с MMSE.
Множественный доступ с сигнатурами, основанными на перемежении или скремблировании
Теперь рассмотрим ещё один класс методов множественного доступа с кодовым разделением – это методы, в которых сигнатуры получены на основе перемежения или скремблирования битов или символов. Основная цель перемежения – борьба с пакетными ошибками путём распределения этих ошибок среди многих блоков данных. Эти распределённые биты ошибок получают свою идентификацию в соответствующих блоках и поэтому могут быть обнаружены и исправлены с помощью любых кодов с обнаружением и исправлением ошибок.
В системах такого типа используются достаточно длинные последовательности, тогда как в системах предыдущих типов используются короткие сигнатуры. Например, к данному классу относится система множественного доступа, основанного на перемежении (interleave division multiple access, IDMA). В методе IDMA, используя различные перемежители для различных пользователей, удаётся уменьшить помеху множественного доступа. Пример фактор-графа для случая двух пользователей приведён на рис. 8.
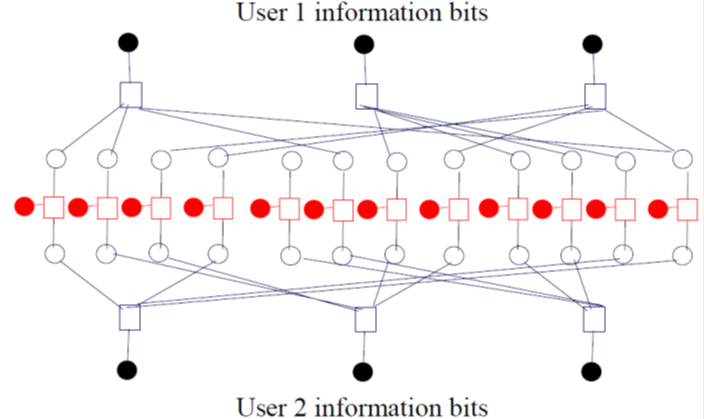
На приёмной стороне производится декодирование принятых сигналов с использованием многопользовательского приёмника. Ансамбль сигнатур в IDMA содержит большое число неортогональных последовательностей, позволяя таким образом обеспечить одновременный доступ для большого числа пользователей.
Разновидность метода IDMA – сгруппированный множественный доступ с разделением на основе перемежения (grouped-IDMA). Он отличается тем, что активные пользователи разбиваются на несколько групп и каждой группе присваивается свой ортогональный код. Эта схема сочетает в себе преимущества IDMA и ортогонального CDMA. Производительность сгруппированного метода IDMA выше, чем простого IDMA, когда число пользователей относительно велико, особенно при низких или средних значениях отношения сигнал/шум.
Для системы связи с K пользователями, разделёнными на G групп, сгруппированный IDMA можно рассматривать как простой IDMA при G = 1, как ортогональный CDMA при G = K или как собственно сгруппированный IDMA при .
К классу методов, основанных на перемежении, относятся также ещё несколько методов: множественный доступ с решётчатым перемежением (interleave grid multiple access, IGMA), множественный доступ с разделением на основе повторения (repetition division multiple access, RDMA) и множественный доступ с расширением ресурсов (resource spread multiple access, RSMA).
Методы перемежения, скремблирования и канального кодирования используются для уменьшения взаимной корреляции между сигнатурами, принадлежащими разным пользователям. Поток битов каждого пользователя сначала кодируется специальным канальным кодом переменной скорости, затем производится расширение спектра и скремблирование.
На приёмной стороне суммарный сигнал сначала проходит процедуру, обратную расширению спектра, затем процедуру, обратную скремблированию, после чего декодер вычисляет оценки битов пользователей и, наконец, происходит декодирование канального кода каждого пользователя. Декодирование в системах RDMA и RSMA осуществляется методом MMSE-SIC, а в системах IDMA и IGMA – методом оценки сигнала с параллельной компенсацией помех (elementary signal estimator-parallel interference cancellation, ESE-PIC).
Все рассмотренные классы методов – потенциальные кандидаты для использования в новых системах радиосвязи.
Множественный доступ с битовым разделением
Как известно, каждый символ сигнального созвездия кодируется двумя, тремя, четырьмя или бо́льшим числом битов. Битовое разделение основано на том, что разные биты в одном символе распределяются между разными пользователями.
Итак, основная технология, использующая разделение битов в символе – это мультиплексирование с битовым разделением (bit division multiplexing, BDM). Она может применяться только в нисходящем канале (т.е. от базовой станции к абонентам). В системе BDM возможно гибкое перераспределение битов внутри передаваемого символа между несколькими пользователями. Это позволяет изменять скорость передачи данных в зависимости от состояния канала. Данная система отличается простотой декодирования, т.к. для в ней применяется классический демодулятор QAM, в отличие от вычислительно затратных многопользовательских приёмников.
Ещё один метод, относящийся к данному классу – множественный доступ с расширением сигнального созвездия (constellation expansion multiple access, CEMA). В этом методе одновременно передаются потоки данных многих пользователей, имеющих близкие значения отношения сигнал/шум. Потоки объединяются путём отображения кодированных битов каждого потока на точки сигнального созвездия согласно изменяющемуся во времени шаблону. Этот шаблон разработан таким образом, чтобы обеспечить для всех потоков одинаковый уровень защиты от ошибок. Многопользовательские потоки данных могут параллельно передаваться в одних и тех же частотно-временных ресурсных блоках системы OFDMA. Одновременно можно передать большее число потоков, чем в обычной системе OFDMA, благодаря чему достигается более высокая спектральная эффективность.
Существуют две усовершенствованные разновидности CEMA: множественный доступ с адаптивным по скорости расширением созвездия (rate-adaptive constellation expansion multiple access, RA-CEMA или REMA) и NOMA с эквидистантным созвездием (NOMA with equal distance constellation, EDC-NOMA).
Технология REMA – неортогональная схема передачи, она подобно PD-NOMA передаёт информационные сигналы параллельно нескольким пользователям в одной и той же полосе частот и в одном и том же временном слоте. Основная идея REMA состоит в комбинировании информационных сигналов на битовом уровне так, чтобы комбинированные символы находились на равных расстояниях в комбинированных сигнальных созвездиях. Использование созвездия с равными расстояниями приводит к уменьшению величины вектора ошибок.
На рис. 9 приведён пример сигнального созвездия в случае модуляции QAM-16 и двух пользователей в схеме REMA. Чёрным цветом обозначены биты, предназначенные первому
(дальнему) пользователю, красным цветом – биты, предназначенные второму (ближнему)
пользователю.

Разделение пользователей на приёмнике и демодуляция в схеме REMA осуществляется методом максимального правдоподобия либо методом последовательной компенсации помех (SIC).
Также была предложена модифицированная схема REMA, отличающаяся тем, что в ней используется многоуровневое кодирование. Информационные биты разделяются на l потоков, каждый из которых кодируется независимо с как можно более различающимися кодовыми скоростями. Затем l кодовых битов отображаются на сигнальное созвездие с помощью амплитудно-импульсной модуляции порядка 2l.
Следующая разновидность методов множественного доступа с битовым разделением – NOMA на основе модуляции (modulation based NOMA, M-NOMA). В методе M-NOMA используется модуляция для создания ортогональности между пользователями. Этот метод не только упрощает систему, но и улучшает её общую производительность по сравнению с существующими методами NOMA. В M-NOMA базовая станция разделяет ближних и дальних пользователей с помощью модуляции. Ближние пользователи модулируются с помощью действительной компоненты комплексных символов созвездия QPSK (четырёхпозиционной фазовой модуляции), а дальние – с помощью мнимой компоненты. Метод M-NOMA позволяет уменьшить частоту символьных ошибок, межсотовые и межкластерные помехи, задержку и вычислительную сложность. Метод M-NOMA обладает лучшей производительностью по сравнению с обычным NOMA с точки зрения скорости передачи данных и помех.
Отметим основной недостаток методов множественного доступа с битовым разделением: чем сложнее схема модуляции, тем бо́льшее влияние оказывают искажения при передаче и тем меньше расстояние от базовой станции, на котором сигнал может быть успешно принят.
Ещё один метод, который можно отнести к данному классу – ортогональный множественный доступ на основе строительных блоков разреженного созвездия (building block sparse constellation based orthogonal multiple access, BOMA). В этом методе происходит добавление передаваемой информации от пользователя с хорошей информацией о состоянии канала (CSI) к символам пользователя с плохой CSI (рис. 10), при этом ёмкость многопользовательской системы значительно увеличивается.
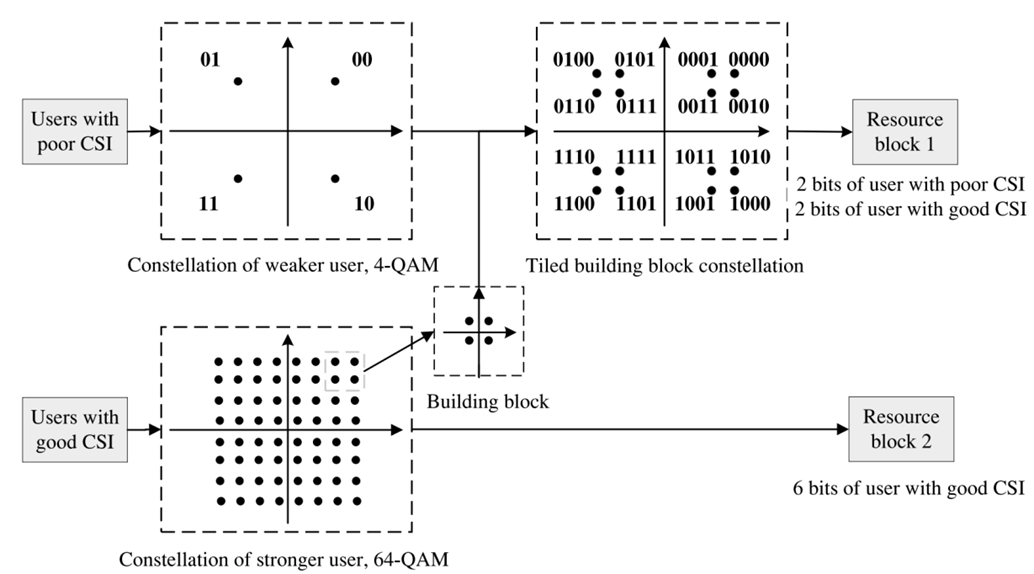
В рамках BOMA пользователь с плохой CSI (B-пользователь) использует созвездие с большим минимальным расстоянием, таким, чтобы для B-пользователя величина вероятности битовой ошибки была той же, что и у пользователя с хорошей CSI (G-пользователь). Каждая точка созвездия B-пользователя расщепляется на несколько точек подсозвездия с меньшим расстоянием между точками. С помощью этих подсозвездий и происходит передача информации для G-пользователя, т.к. он в состоянии разделить эти точки. B-пользователь воспринимает каждое такое подсозвездие как отдельную точку, и информация для B-пользователя кодируется расположением подсозвездия как целого.
Структура передатчика и приёмника BOMA проста и похожа на принятую в современных системах 4G. Требуются лишь незначительные изменения программного обеспечения, чтобы можно было внедрить технологию BOMA в сочетании с массивным MIMO и другими требованиями для перспективных радиосистем. Кроме того, технология BOMA не требует сложного распределения мощности и использования приёмника SIC, которые необходимы для других неортогональных схем. Однако, в этой технологии требуется сопряжение пользователей, что снижает её гибкость.
Отметим, что битовое пространство разделения пользователей не является независимым ресурсным пространством. Способ распределения битов внутри символа сигнального созвездия между различными пользователями можно рассматривать как разновидность кодирования, поэтому битовое разделение пользователей мы отнесли к классу кодового разделения.
Заключение
В третьей части мы рассмотрели как ортогональные, так и неортогональные методы множественного доступа с кодовым разделением пользователей, ведь без этих методов невозможно обойтись при проектировании современных систем связи. Рассмотрели основные преимущества и недостатки этих технологий. Хочу отметить, что в большинстве неортогональных методов отсутствует строгая теория построения кодовых сигнатур, при этом кодовые книги получают с помощью различных вычислительных алгоритмов, оптимальность которых остаётся под вопросом.
В четвёртой части статьи из серии “Обзор методов множественного доступа в беспроводной связи” вас ждут методы множественного доступа, основанные на пространственном разделении пользователей.
Hidden text
1. Zigangirov K.Sh. Theory of code division multiple access communication. – John Wiley & Sons, 2004.
2. Бабков В.Ю., Никитин А.Н., Осенний К.Н. Системы мобильной связи с кодовым разделением каналов. – СПб: Триада, 2003. – 239 с.
3. Li Daoben. The perspectives of large area synchronous CDMA technology for the fourth-generation mobile radio // IEEE Communications Magazine. – 2003. – Vol. 41, no. 3. – P. 114-118.
4. Hoshyar Reza, Wathan Ferry P, Tafazolli Rahim. Novel low density signature for synchronous CDMA systems over AWGN channel // IEEE Transactions on Signal Processing. – 2008. – Vol. 56, no. 4. – P. 1616-1626.
5. Hoshyar R., Razavi R., Al-Imari M. LDS-OFDM an efficient multiple access technique //2010 IEEE 71st Vehicular Technology Conference. – 2010. – P. 1-5.
6. A high performance joint detection and decoding scheme for LDPC coded SCMA system / Kaining Han, Zhenbing Zhang, Jianhao Hu, Jienan Chen // 2016 IEEE Globecom Workshops. – 2016. – P. 1-6.
7. Luo Fa-Long, Zhang Charlie. Signal processing for 5G: algorithms and implementations. –John Wiley & Sons, 2016.
8. Nikopour Hosein, Baligh Hadi. Sparse code multiple access // 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC) / IEEE. –– 2013. – P. 332-336.
9. Покаместов Д.А., Демидов А.Я., Крюков Я.В. Влияние формирующих матриц на помехозащищенность каналов связи с множественным доступом на основе разреженных кодов // Доклады Томского государственного университета систем управления и радиоэлектроники. – 2016. – Т. 19, № 3. – С. 65-69.
10. Климентьев В.П. Методы приёма сигналов в системах множественного доступа с разреженным кодированием : дис. … канд. наук / В.П. Климентьев. – Санкт-Петербург. – 2018. –167 с.
11. Successive interference cancelation amenable multiple access (SAMA) for future wireless communications / Xiaoming Dai, Shanzhi Chen, Shaohui Sun et al. // 2014 IEEE International Conference on Communication Systems / IEEE. – 2014. – P. 222-226.
12. Yuan Z, Yu G, Li W. Multi-user shared access for 5G // Telecommun. Network Technology. – 2015. – Vol. 5, no. 5. – P. 28-30.
13. Interleave division multiple-access / Li Ping, Lihai Liu, Keying Wu, Wai Kong Leung // IEEE transactions on wireless communications. – 2006. – Vol. 5, no. 4. – P. 938-947.
14. Tu Yifeng, Fan Pingzhi, Zhou Gao. Grouped interleave-division multiple access // 2006 First International Conference on Communications and Networking in China. – IEEE, 2006. – P. 1-5.
15. Meric Hugo, Piquer Jose Miguel. Performance Evaluation of Bit Division Multiplexing combined with Non-Uniform QAM // European Wireless 2014; 20th European Wireless Conference / VDE. – 2014. – P. 1-5.
16. Perotti A.G., van de Beek Jaap, Popovic B.M. Downlink overloaded multiple access based on constellation expansion // 2014 IEEE Globecom Workshops. – 2014. – P. 977-982.
17. Perotti A.G., Popovic B.M. Non-orthogonal multiple access for degraded broadcast channels: RA-CEMA // 2015 IEEE Wireless Communications and Networking Conference. – 2015. – P. 735-740.
18. Lue Hsin-Yu. Design and Performance Analysis of Modified Non-Orthogonal Multiple Access : Ph. D. thesis / Hsin-Yu Lue; Hsinchu. – 2015. – 42 p.
19. Modulation Based Non-Orthogonal Multiple Access for 5G Resilient Networks / Rabia Khan, Dushantha Nalin K Jayakody, Haris Pervaiz, Rahim Tafazolli // 2018 IEEE Globecom Workshops. – 2018. – P. 1-6.
20. Yu Bo, J. Fonseka. Throughput Enhancement on the Downlink of 4G and 5G Systems: NOMA, BOMA and IBOMA // International Journal of Sensors, Wireless Communications and Control. – 2018. – Vol. 8, no. 1. – P. 57-64

