В последнее время все большую популярность набирает электронная подпись Ed25519, основанная на разновидности эллиптической кривой, предложенной Бернштейном. По мере увеличения числа узлов I2P с данным видом подписи возникла необходимость ее поддержки в своей реализации I2P, поскольку Ed25519 не входит в состав популярных криптографических библиотек. Как правило используются разновидности ref10 из библиотеки SUPERCOP, реализованной самим Бернштейном на ассемблере, и затем портированной на другие языки. Данная реализация работает хорошо и быстро, однако у нее есть главный недостаток — она непонятна. Действительно, если заглянуть в исходный код, то можно увидеть большое количество однотипных строк, оперирующих с множеством «магических» чисел, понять же, что они означают, без углубления в теорию не представляется возможным. Целью данной статьи является математически прозрачная реализация Ed22519, используя лишь стандартные операции с большими числами, присутствующие в любой криптографической библиотеке, со скоростью работы, достаточной для практического использования в I2P.

Принцип работы эллиптической криптографии

Задается неявное уравнение плоской кривой специального вида, называемого эллиптической кривой. Задается простое число, образующее поле вычетов по модулю. Координаты точек кривой принадлежат этому полю, т.е. являются целыми неотрицательными числами, не превышающее модуль. Над двумя точками кривой задается операция сложения таким образом, чтобы новая точка также принадлежала кривой. Если точку сложить саму с собой то получится умножение на 2, если прибавить еще раз — то на 3, и так далее умножение на произвольное число n. Также вместе с кривой задается базовая точка, принадлежащая кривой, операции над которой и используются в криптографии.
Для криптографии выбирается произвольное большое число n, являющееся секретным ключем, на него умножается базовая точка и новая точка служит публичным ключем, который затем умножается противоположной стороной на другое число с целью согласования ключа или проверки подписи. Стойкость основывается отсутствием на данный момент известного способа определения множителя по точке за разумное время

Ed25519

Берштейн предложил использовать эллиптическую кривую со следующими параметрами.
Уравнение кривой:
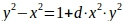, где
Модуль:
q =
отсюда и возникло название кривой.

Базовая точка:
(x, 4/5), где x получается решением уравнения (см. ниже)
Ее координаты в явном виде:
x=15112221349535400772501151409588531511454012693041857206046113283949847762202,
y=46316835694926478169428394003475163141307993866256225615783033603165251855960.

Сложение:
, где

Следует заметить, что деление здесь это не обычное деление с остатком, а умножение на обратный по модулю элемент, вычисляемый согласно малой теоремы Ферма по формуле , т. е. операция возведения в степень по модулю.

В качестве публичного ключа предлагается использовать только координату y, при необходимости решая уравнения кривой относительно х, и вычисляя его по формуле .

Поскольку q представимо в виде 8*k+5, то для вычисления квадратного корня из х следует воспользоваться формулой . Действительно q = = , отсюда квадратный корень .

Реализация

Код полностью располагается по по адресу в файле Signature.cpp. Для работы с большими числами используются функции библиотеки BN из openssl.
Создадим класс Ed25519, реализующий саму кривую, и содержащий параметры кривой, рассчитываемые в его конструкторе. В первую очередь необходимы 3 метода: сложение, умножение на число и вычисление x по заданному y.

class Ed25519
{
//... 
    EDDSAPoint Sum (const EDDSAPoint& p1, const EDDSAPoint& p2) const
    EDDSAPoint Mul (const EDDSAPoint& p, const BIGNUM * e) const
    BIGNUM * RecoverX (const BIGNUM * y) const
//...
}

Из-за частного использования операция сложения и трудоемкости операции деления, приведем x и y к общему знаменателю (1+m)*(1-m), тем самым избавившись от одного деления. В результате код для сложения выглядит примерно так:

// m = d*p1.x*p2.x*p1.y*p2.y
BN_mul (xx, p1.x, p2.x, m_Ctx); //p1.x*p2.x
BN_mul (yy, p1.y, p2.y, m_Ctx);  //p1.y*p2.y
BIGNUM * m = BN_dup (d);
BN_mul (m, m, xx, m_Ctx);
BN_mul (m, m, yy, m_Ctx);
// x = (p1.x*p2.y + p2.x*p1.y)*inv(1 + m)
// y = (p1.y*p2.y + p1.x*p2.x)*inv(1 - m)
// m1 = 1-m
BN_one (m1);
BN_sub (m1, m1, m);
// m = m+1
BN_add_word (m, 1);		
// y = (p1.y*p2.y + p1.x*p2.x)*m	
BN_add (y, xx, yy);
BN_mod_mul (y, y, m, q, m_Ctx);
// x = (p1.x*p2.y + p2.x*p1.y)*m1
BN_mul (yy, p1.x, p2.y, m_Ctx);
BN_mul (xx, p2.x, p1.y, m_Ctx);
BN_add (x, xx, yy);
// denominator m = m*m1	
BN_mod_mul (m, m, m1, q, m_Ctx);
Inv (m); 	
BN_mod_mul (x, x, m, q, m_Ctx); // x = x/m
BN_mod_mul (y, y, m, q, m_Ctx); // y = y/m

Также для удвоения (сложения точки самой с собой) реализован отдельный метод Double, поскольку в этом случае p1.x = p2.x и p1.y = p2.y, что позволяет сократить число умножений. Кроме того, вместо BN_mul используется более быстрая BN_sqr.
Умножение релизовано простейшим методом удвоения и прибавления, т.е. идти вдоль числа побитово от старшего к младшему, на каждом шаге удваивать значение результата, а если бит — единица, то прибавлять умножаемую точку.

EDDSAPoint res {zero, one};
if (!BN_is_zero (e))
{
    int bitCount = BN_num_bits (e);
    for (int i = bitCount - 1; i >= 0; i--)
    {
        res = Double (res);
        if (BN_is_bit_set (e, i)) res = Sum (res, p);
    }
}	

Вычисление x по y реализовано тривиально.
Сначала подкоренное выражение:

BN_sqr (y2, y, m_Ctx); // y^2
// xx = (y^2 -1)*inv(d*y^2 +1) 
BN_mul (xx, d, y2, m_Ctx);
BN_add_word (xx, 1);
Inv (xx);
BN_sub_word (y2, 1);
BN_mul (xx, y2, xx, m_Ctx);

Затем вычисление квадратного корня по формуле

// x = srqt(xx) = xx^(2^252-2)		
BN_mod_exp (x, xx, two_252_2, q, m_Ctx);

Подпись и проверка подписи

Данная тема достаточно интересна и обширна, потому этому вопросу будет посвящена отдельная статья. В то же время методы Sign и Verify реализованы и используются практически. Потому, кому интересно, можно глянуть в код. Здесь же будут лишь перечислены некоторые особенности.
Как и другие системы электронной подписи, подпись EdDSA представляет собой пару 32-х байтных чисел (R,S), потому длина подписи — 64 байта.
Числа представлены в Little Endian.
В качестве хэш-функции используется SHA-512.
При подписи случайное число не генерируется, вместо этого используется правая половина SHA-512 хэша от секретного ключа, объединенный с самими подписываемыми данными.
Также используется простое число 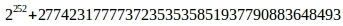, использовавшееся при выборе базовой точки, с тем расчетом, чтобы умножение на него базовой точки давало нуль.

Заключение

Очевидно, что самым медленным местом данной реализации является деление в операции сложения. На самом деле, пользуясь современными достижениями теории чисел и спецификой параметров EdDSA, можно исключить его полностью, как это сделано в ref10. Однако это существенно усложнит реализацию и сделает ее менее понятной, потому этим следует заниматься только если возникнет реальная практическая необходимость. В настоящее время проверка подписи EdDSA в I2P довольно редкое событие, по сравнению, скажем, с шифрованием по схеме Эль-Гамаля.
Существует мнение, что реализация собственной криптографии это крайне плохая идея. Однако использование непонятно как работающей реализации представляется немногим лучше. Кроме того, данная статья может быть полезна тому, кому интересно докопаться до сути, а работающий практический код поможет в этом.