В предыдущей статье была рассмотрена реализация самой кривой Ed25519, операции сложения и умножения на число, восстановление второй координаты. В данной статье рассматриваются вопросы эффективного использования этих операций для электронной подписи сообщений и работы в I2P.
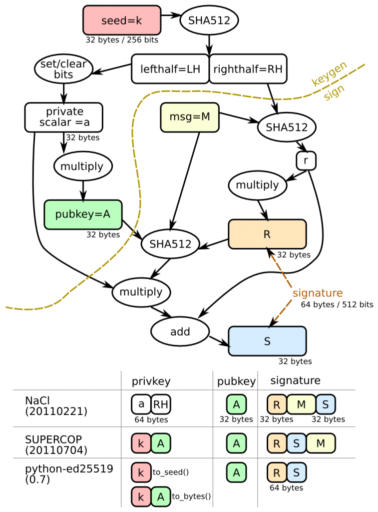
В отличие от RSA, где секретный и публичный ключ можно использовать непосредственно, здесь приходится использовать более сложную схему и вводить некоторый дополнительный объект. EdDSA концептуально реализует алгоритм DSA, распространяя его на случай кривых. В качестве подписи выступает пара чисел (R,S), для EdDSA каждое длиной 32 байта, итого длина подписи — 64 байта. Подписываются не сами данные, а хэш он них. В качестве хэш-функции используется SHA512. Далее малым буквами будут обозначаться числа, а большими буквами — соответствующая точка на кривой, полученная умножением числа на базовую точку B.
Пусть h — хэш подписываемого сообщения, a — секретный ключ, а A — соответствующий ему публичный ключ (A = a*B). Возьмем случайное число r, и вычислим R = r*B и s = r+h*a. Пара (R,s) будет подписью, где R представлена своей координатой y.
При проверки подписи получателю известны A и h и надо проверить истинность (R,s). Для этого проверяется равенство: s*B = R+h*A.
Действительно (r+h*a)*B = r*B+h*a*B = R+h*A.
Заметим, что s вычисляется непосредственно на основе секретного ключа, а не порожденной им точки, потому ошибки в реализации могут провести к немедленной его компрометации. В частности, неудачный выбор r. Во избежание этого Бернштейн предлагает вычислять r как хэш от половины хэша секретного ключа, объединенной с самими подписываемыми данными, однако выбор r каким нибудь другим способом не нарушит работоспособность алгоритма, то есть, сами значения подписи будут другими, но результат проверки будет тем же. Мы же будем вычислять r, как предлагает Бернштейн и как это делается в официальном I2P.
Для дальнейших вычислений потребуется ранее не использовавшийся параметр кривой l=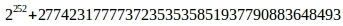
, такой что l*B=0.
Из этого равенства немедленно следует, что значения множителя перед точкой не должно превышать l, в противном случае это будет лишь приводить к увеличению объема вычислений. Если множитель превышает l, то он должен браться по модулю, в частности значение h, являющееся хэшем SHA512 длиной 64 байта.
Из этого, в свою очередь, следует, что множитель в операции умножения не превышает 32 байт и старший бит всегда нулевой.
Как можно видеть из формул, для подписи требуется одно умножение на базовую точку, а для проверки подписи — два: одно на базовую точку, а второе на публичный ключ.
Для базовой точки имеет смысл рассчитать результат умножения на разные множители заранее. Самое простое это ряд (B, 2*B, 4*B, 8*B, ...) всего 255 точек, что позволяет на каждом шаге исключить операцию удвоения. Можно пойти дальше и разложить множитель не по степеням двойки, а по степеням 16 и для каждых 4-х бит множителя прибавлять к результату рассчитанную точку из массива. Для этого потребуется рассчитать и хранить 32*2*16 точек, но это делается единожды на время всей работы. Таким образом, умножение на B сводится ровно к 64 сложениями и подпись сообщения осуществляется быстро. Вот как это выглядит в коде.
Здесь Bi16 это массив их 64x16 точек, а e это 32-байтный множитель в Little Endian. Вместо степеней 16 можно использовать разложения по степеням 256, это приведет к некоторому ускорению, в то же время потребуется хранить уже 32*256 точек.
Для проверки подписи потребуется умножение также и публичного ключа, хотя он и является результатом умножения B, множитель нам неизвестен, поскольку это и есть секретный ключ. Если применить данный способ, то придется держать такой массив для каждого из них, а в I2P публичных ключей много — для каждого узла из netdb свой, которых порядка несколько тысяч, что привело бы к неоправданному расходу памяти. Поэтому, чтобы достигнуть скорости работы, сравнимой с другими эллиптическими кривыми, придется усовершенствовать операцию сложения.
Как было отмечено в предыдущей статье, самой медленной операцией является деление при каждом сложении, от которого можно избавиться, перейдя к однородным координатам. Реализация становится менее наглядной, однако все реализации эллиптической криптографии устроены именно там. Вместо двух координат точки (x, y) вводится третья координата, хранящая общий знаменатель, а вместо x и y хранятся их числители, то есть из однородных координат (X,Y,Z) истинные координаты получаются как (X/Z, Y/Z). Кроме того, вводится четвертая координата T = X*Y/Z. Координаты результата сложения вычисляются по следующим формулам:
X = (X1*Y2+Y1*X2)*(Z1*Z2-d*T1*T2)
Y = (Y1*Y2+X1*X2)*(Z1*Z2+d*T1*T2)
Z = (Z1*Z2-d*T1*T2)*(Z1*Z2+d*T1*T2)
T = (Y1*Y2+X1*X2)*(X1*Y2+Y1*X2)
Как видно, трудоемкая операция возведения в степень в процессе сложения и умножения более не применяется.
Другим недостатком однородных координат является трудоемкость сравнения двух точек: координаты X и Y нельзя сравнивать непосредственно — их нужно тем или иным способом привести к общему знаменателю, что требует дополнительных вычислений. Для проверки же подписи требуется сравнивать точки.
Перепишем выражение для проверки подписи s*B=R+h*A в виде R=s*B-h*A.
Тогда, вместо восстановления координаты X точки по координате Y из подписи, можно взять координату Y из (s*B-h*A), тем самым экономя еще одно возведение в степень и сравнивая числа вместо точек. Данный способ требует операции вычитания, которая реализована через сложения и унарный минус, определяемый как (-X, Y, Z, -T). Таким образом, операция вычитания выполняется с той же скоростью что и сложение, и может быть использована для разложения по степеням с отрицательными коэффициентами, что позволяет уменьшить объем памяти в 2 раза.
Длина I2P адреса с EdDSA — 391 байт, код типа подписи — 7, обозначается в документации как EdDSA_SHA512_Ed25519.
Длина секретного и публичного ключей — 32 байта, длина подписи 64 байта, первые 32 байта идет R в форме координаты y, вторые 32 байта — s.
Все числа передаются в Little Endian.
На настоящий момент EdDSA является рекомендованным типом подписи для RouterInfo.
Таким образом, в двух статьях описана полная и прозрачная реализация EdDSA поверх библиотеки для работы с большими числами из библиотеки openssl, работающая с высокой скоростью и практически используемая в i2pd.
Алгоритм подписи EdDSA
В отличие от RSA, где секретный и публичный ключ можно использовать непосредственно, здесь приходится использовать более сложную схему и вводить некоторый дополнительный объект. EdDSA концептуально реализует алгоритм DSA, распространяя его на случай кривых. В качестве подписи выступает пара чисел (R,S), для EdDSA каждое длиной 32 байта, итого длина подписи — 64 байта. Подписываются не сами данные, а хэш он них. В качестве хэш-функции используется SHA512. Далее малым буквами будут обозначаться числа, а большими буквами — соответствующая точка на кривой, полученная умножением числа на базовую точку B.
Пусть h — хэш подписываемого сообщения, a — секретный ключ, а A — соответствующий ему публичный ключ (A = a*B). Возьмем случайное число r, и вычислим R = r*B и s = r+h*a. Пара (R,s) будет подписью, где R представлена своей координатой y.
При проверки подписи получателю известны A и h и надо проверить истинность (R,s). Для этого проверяется равенство: s*B = R+h*A.
Действительно (r+h*a)*B = r*B+h*a*B = R+h*A.
Заметим, что s вычисляется непосредственно на основе секретного ключа, а не порожденной им точки, потому ошибки в реализации могут провести к немедленной его компрометации. В частности, неудачный выбор r. Во избежание этого Бернштейн предлагает вычислять r как хэш от половины хэша секретного ключа, объединенной с самими подписываемыми данными, однако выбор r каким нибудь другим способом не нарушит работоспособность алгоритма, то есть, сами значения подписи будут другими, но результат проверки будет тем же. Мы же будем вычислять r, как предлагает Бернштейн и как это делается в официальном I2P.
Эффективная реализация умножения
Для дальнейших вычислений потребуется ранее не использовавшийся параметр кривой l=
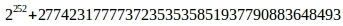, такой что l*B=0. Из этого равенства немедленно следует, что значения множителя перед точкой не должно превышать l, в противном случае это будет лишь приводить к увеличению объема вычислений. Если множитель превышает l, то он должен браться по модулю, в частности значение h, являющееся хэшем SHA512 длиной 64 байта.
Из этого, в свою очередь, следует, что множитель в операции умножения не превышает 32 байт и старший бит всегда нулевой.
Как можно видеть из формул, для подписи требуется одно умножение на базовую точку, а для проверки подписи — два: одно на базовую точку, а второе на публичный ключ.
Для базовой точки имеет смысл рассчитать результат умножения на разные множители заранее. Самое простое это ряд (B, 2*B, 4*B, 8*B, ...) всего 255 точек, что позволяет на каждом шаге исключить операцию удвоения. Можно пойти дальше и разложить множитель не по степеням двойки, а по степеням 16 и для каждых 4-х бит множителя прибавлять к результату рассчитанную точку из массива. Для этого потребуется рассчитать и хранить 32*2*16 точек, но это делается единожды на время всей работы. Таким образом, умножение на B сводится ровно к 64 сложениями и подпись сообщения осуществляется быстро. Вот как это выглядит в коде.
EDDSAPoint res {zero, one};
for (int i = 0; i < 32; i++)
{
uint8_t x = e[i] & 0x0F; // 4 low bits
if (x > 0)
res = Sum (res, Bi16[i*2][x-1], ctx);
x = e[i] >> 4; // 4 high bits
if (x > 0)
res = Sum (res, Bi16[i*2+1][x-1], ctx);
}
Здесь Bi16 это массив их 64x16 точек, а e это 32-байтный множитель в Little Endian. Вместо степеней 16 можно использовать разложения по степеням 256, это приведет к некоторому ускорению, в то же время потребуется хранить уже 32*256 точек.
Для проверки подписи потребуется умножение также и публичного ключа, хотя он и является результатом умножения B, множитель нам неизвестен, поскольку это и есть секретный ключ. Если применить данный способ, то придется держать такой массив для каждого из них, а в I2P публичных ключей много — для каждого узла из netdb свой, которых порядка несколько тысяч, что привело бы к неоправданному расходу памяти. Поэтому, чтобы достигнуть скорости работы, сравнимой с другими эллиптическими кривыми, придется усовершенствовать операцию сложения.
Сложение в однородных координатах
Как было отмечено в предыдущей статье, самой медленной операцией является деление при каждом сложении, от которого можно избавиться, перейдя к однородным координатам. Реализация становится менее наглядной, однако все реализации эллиптической криптографии устроены именно там. Вместо двух координат точки (x, y) вводится третья координата, хранящая общий знаменатель, а вместо x и y хранятся их числители, то есть из однородных координат (X,Y,Z) истинные координаты получаются как (X/Z, Y/Z). Кроме того, вводится четвертая координата T = X*Y/Z. Координаты результата сложения вычисляются по следующим формулам:
X = (X1*Y2+Y1*X2)*(Z1*Z2-d*T1*T2)
Y = (Y1*Y2+X1*X2)*(Z1*Z2+d*T1*T2)
Z = (Z1*Z2-d*T1*T2)*(Z1*Z2+d*T1*T2)
T = (Y1*Y2+X1*X2)*(X1*Y2+Y1*X2)
Как видно, трудоемкая операция возведения в степень в процессе сложения и умножения более не применяется.
Другим недостатком однородных координат является трудоемкость сравнения двух точек: координаты X и Y нельзя сравнивать непосредственно — их нужно тем или иным способом привести к общему знаменателю, что требует дополнительных вычислений. Для проверки же подписи требуется сравнивать точки.
Вычитание двух точек кривой
Перепишем выражение для проверки подписи s*B=R+h*A в виде R=s*B-h*A.
Тогда, вместо восстановления координаты X точки по координате Y из подписи, можно взять координату Y из (s*B-h*A), тем самым экономя еще одно возведение в степень и сравнивая числа вместо точек. Данный способ требует операции вычитания, которая реализована через сложения и унарный минус, определяемый как (-X, Y, Z, -T). Таким образом, операция вычитания выполняется с той же скоростью что и сложение, и может быть использована для разложения по степеням с отрицательными коэффициентами, что позволяет уменьшить объем памяти в 2 раза.
Адреса I2P с EdDSA
Длина I2P адреса с EdDSA — 391 байт, код типа подписи — 7, обозначается в документации как EdDSA_SHA512_Ed25519.
Длина секретного и публичного ключей — 32 байта, длина подписи 64 байта, первые 32 байта идет R в форме координаты y, вторые 32 байта — s.
Все числа передаются в Little Endian.
На настоящий момент EdDSA является рекомендованным типом подписи для RouterInfo.
Таким образом, в двух статьях описана полная и прозрачная реализация EdDSA поверх библиотеки для работы с большими числами из библиотеки openssl, работающая с высокой скоростью и практически используемая в i2pd.
gurinderu
Спасибо вам, за ваши старания в области I2P, особенно за плюсовую версию i2pd.