Одна из основных проблем человека, который занимается машинным обучением, - данные. Исследователи сталкиваются с плохим качеством данных и/или их отсутствием. Рассмотрим способы улучшение метрик классификатора в условиях малого количества признаков.

В машинном обучении одним из основных критериев успеха является правильная предобработка данных. В условиях отсутствия дополнительных факторов качество классификатора можно улучшить за счет обеспечения монотонности целевой переменной от признаков, а также за счет увеличения порядка пространства признаков.

Цель кейса, рассматриваемого в этой статье: определить, куда доставлялся заказ, основываясь на двух признаках: времени размещения и времени доставки.

Что делаем

1. Преобразовываем время к удобному формату.

2. Строим графики для генерации гипотез.

3. Строим классификатор №1 и визуализируем результаты.

4. Обеспечиваем монотонность целевой переменной, строим классификатор №2.1. Увеличиваем порядок пространства признаков, строим классификатор №2.2.

5. Обеспечиваем монотонность целевой переменной и увеличиваем порядок пространства признаков одновременно, строим классификатор №3, наблюдаем улучшение метрик.

В файле представлены данные заказов одного дня кафе, которое принимает заказы на готовую еду и доставляет ее клиентам.

Таблица содержит 3 столбца:

1. Order_time – время оформления заказа в приложении. Формат: 'h:mm:ss'

2. Delivery_time – время доставки заказа в минутах

3. Office – бинарная переменная. Равна 1, если доставка осуществлялась в офис. Равна 0, если доставка осуществлялась в жилой сектор.

Цель: определить, куда доставлялся заказ.

Импортируем библиотеки, данные.

from random import randint, betavariate
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
from datetime import datetime, timedelta, date, time
import pylab
import seaborn as sns
plt.style.use('seaborn')
%matplotlib inline
pylab.rcParams['figure.figsize'] = (15, 10)

df=pd.read_excel('iCafe_train.xlsx') 
df.sample(5)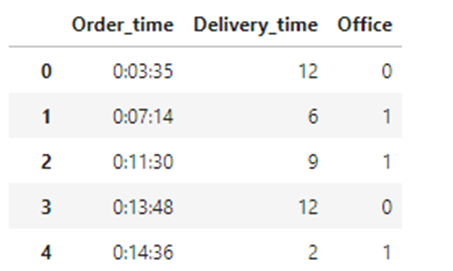

Формат данных столбца Order_time – строка – неудобен для построения классификатора и визуализации, поэтому преобразуем данные к другому виду. Создадим столбец Order_time_sec, в котором будет представлена информация о времени размещения заказа в секундах. Используем две функции:

• to_timedelta модуля pandas, которая распарсит строку времени и определит отклонение результата от 0;

• timedelta64 модуля numpy, которая позволит нам получить в знаменателе 1 секунду и, соответственно, весь результат в секундах. Изменение параметра 's' на 'm' или на 'h' позволит получать результат в минутах и часах соответственно.

df['Order_time_sec'] = pd.to_timedelta(df.Order_time) // np.timedelta64(1,'s') # Создаем столбец
df.sample(5) # Смотрим результат

Чтобы определить какие-либо закономерности, построим графики и проинтерпретируем их.

1. Строим график, где по оси абсцисс откладывается время поступления заказа, а по оси ординат место доставки.

plt.scatter(df.Order_time_sec, df.Office)
plt.xlabel('Время поступления заказа (Order_time_sec)')
plt.ylabel('Место доставки (Office)')
plt.show()

Судя по графику, заказы в офис и не в офис по моменту поступления пересекаются, но кажется, что не очень сильно. Точнее мы сейчас определить не сможем.

2. Строим диаграмму, где на каждое время доставки представлено количество доставок в офис и не в офис

sns.countplot(x = 'Delivery_time', hue = 'Office', data = df)
plt.show()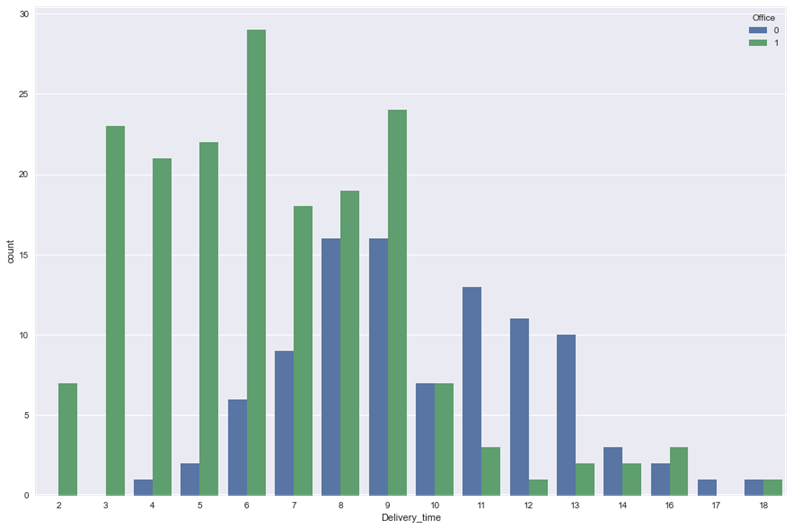

Из диаграммы мы видим, что в среднем в офис поставка осуществляется быстрее. Скорее всего помещение кафе располагается ближе к офисам, чем к жилым кварталам. Также мы видим, что чем дольше время доставки, тем меньше кафе получает заказов.

3. Строим диаграмму, где на каждое время размещения заказа представлено количество доставок в офис и не в офис.

sns.countplot(x = 'Order_time_sec', hue = 'Office', data = df)
plt.show()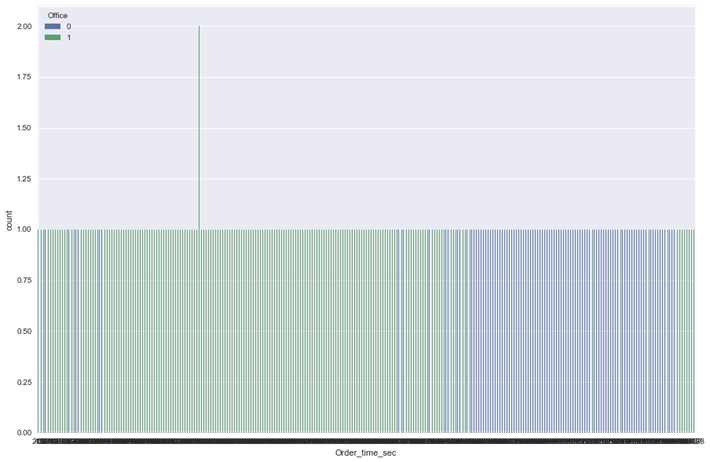

Опять получили лишенный смысла график. Здесь наблюдается следующая проблема: заказы не поступают одновременно (за исключением одного случая, который следует рассматривать как случайное и крайне редкое событие). Для того, чтобы получить информативный график, нам необходимо собрать моменты поступления заказов во временные диапазоны, например, часовые. Создадим столбец Order_time_h, в который запишем час поступления заказа и построим диаграмму на полученных данных.

4. Строим диаграмму, где на каждый час времени размещения заказа представлено количество доставок в офис и не в офис:

df['Order_time_h'] = df.Order_time_sec//3600
sns.countplot(x = 'Order_time_h', hue = 'Office', data = df)
plt.show()

Вот теперь мы видим, что по моменту размещения заказа доля пересечения классов действительно не велика. Так же мы видим, что есть три больших всплеска заказов:

• с 11 до 14 часов в офис – перерыв на поесть;

• с 18 до 22 часов на дом - для тех, кто не хочет или не может готовить ужин;

• с 23 до 1 часа ночи в офис - дежурные на непрерывном производстве (например, техническая поддержка).

5. Построим еще график, которые помогут нам позже построить классификатор:

plt.scatter(df.Order_time_sec[df.Office == 1], df.Delivery_time[df.Office == 1], color = 'red')
plt.scatter(df.Order_time_sec[df.Office == 0], df.Delivery_time[df.Office == 0])
plt.legend(['В офис', 'На дом'])
plt.xlabel('Время поступления заказа (Order_time_sec)')
plt.ylabel('Время доставки заказа (Delivery_time)')
plt.show()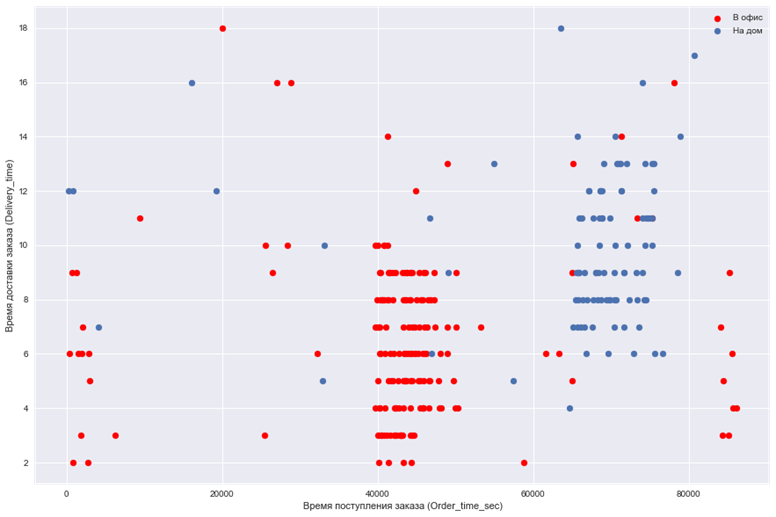

Разрабатываем классификатор №1. Для этого импортируем необходимые инструменты для построения классификатора:

from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
"""Разрабатываем классификатор"""

y = df.Office    # Определяем результирующий признак
X = df[['Order_time_sec', 'Delivery_time']]     # Определяем признаки

С помощью функции train_test_split разбиваем выборку на обучающую и тестовую. Параметр test_size указывает на долю тестовой выборки. Если параметр random_state отличен от None, т.е. имеет конкретное значение, то генерируемые псевдослучайные величины будут иметь одни и те же значения при каждом вызове, и мы будем каждый раз получать одинаковое разбиение на обучающую и тестовую выборки. Условимся, что, random_state=21

X_train, X_test, y_train, y_test = train_test_split (X, y, test_size=0.25, random_state=21)

Функция StandardScaler приведет значения признаков к стандартному виду z = (x-u)/s, где u - среднее значение, а s - стандартное отклонение. Расчет среднего значения и стандартного отклонение осуществляется на выборке для обучения, затем осуществляется преобразования данных для обучения и тестовых данных:

sc = StandardScaler()
sc.fit(X_train) # Находим среднее и стандартное отклонение обучающей выборки
X_train_std = sc.transform(X_train) # Преобразовываем обучающую выборку
X_test_std = sc.transform(X_test) # Преобразовываем тестовую выборку

Формируем классификатор с помощью LogisticRegression. Коэффициенты уравнения логистической регрессии находятся на обучающей выборке, затем с помощью найденного уравнения предсказывается класс объекта на тестовой выборке:

lr = LogisticRegression(random_state=21)
lr.fit(X_train_std, y_train)  # Находим коэффициенты уравнения логистической регрессии
y_pred = lr.predict(X_test_std) # Определяем класс на значениях тестовых данных
print(classification_report(y_test, y_pred))  # Публикуем результаты качества модели на тестовой выборке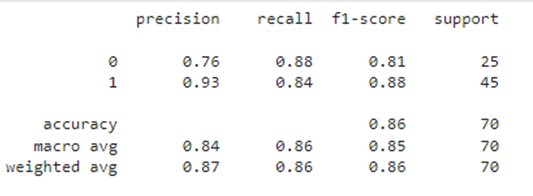

Для анализа полученного результата напишем функцию results(), которой передаются значения:

sc - действующий (полученный при разработке классификатора) метод стандартизации данных;

lr - классификатор;

df - датафрейм;

target - название столбца целевого признака;

attribute_name - список названий столбцов признаков;

name - строка названия анализируемого результата;

def Processing_results(sc, lr, df, target, attribute_name, name):
    X_std = sc.transform(df[attribute_name])
    new_col_name = []
    for i, col_name in enumerate(attribute_name):
        s = col_name + '_std_' + name
        df[s] = X_std[:,i]
        new_col_name.append(s)
    y_pred = 'y_pred_' + name
    Correct = 'Correct_' + name
    df[y_pred] = lr.predict(X_std)
    df[Correct] = df.Office == df[y_pred]
    print(classification_report(df.Office, df[y_pred]))
    
y = 'Office'
x = ['Order_time_sec', 'Delivery_time']
df_train1 = Processing_results(sc, lr, df, y, x, '1')
df_train1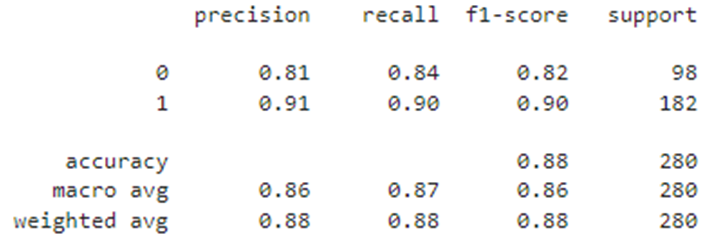

df_test = pd.read_excel('/Users/olgakalinina/Desktop/day02/datasets/iCafe_test.xlsx')
df_test['Order_time_sec'] = pd.to_timedelta(df_test.Order_time)//np.timedelta64(1,'s')
df_t1=df_test

y = 'Office'
x = ['Order_time_sec', 'Delivery_time']
df_test1 = Processing_results(sc, lr, df_t1, y, x, '1')
df_test1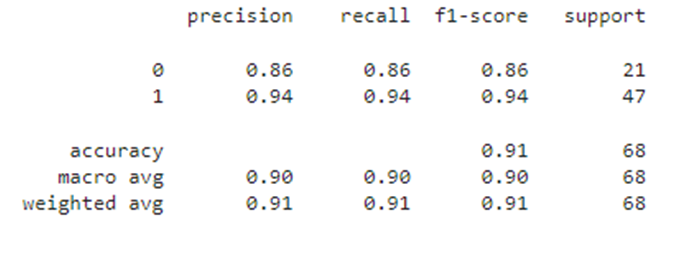

Путем двойного контроля мы убедились, что модель не переобучена и демонстрирует не плохое качество, все метрики на общей обучающей выборке 0.88, на тестовой выборке - 0.91. Можно ли улучшить полученное решение? Для ответа на этот вопрос в начале еще раз посмотрим на графики:

plt.subplot (2, 2, 1)
plt.scatter(df.Order_time_sec[df.Office == 1], df.Delivery_time[df.Office == 1], color = 'red')
plt.scatter(df.Order_time_sec[df.Office == 0], df.Delivery_time[df.Office == 0])
plt.legend(['В офис', 'На дом'])
plt.xlabel('Время поступления заказа (Order_time_sec)')
plt.ylabel('Время доставки заказа (Delivery_time)')
plt.plot([82000, 82000], [0,10], 'red')
plt.plot([82000, 86400], [10,10], 'red')
plt.title('Обучающая выборка, принадлежность к классам')

plt.subplot (2, 2, 2)
plt.scatter(df_test.Order_time_sec[df_test.Office == 1], df_test.Delivery_time[df_test.Office == 1], color = 'red')
plt.scatter(df_test.Order_time_sec[df_test.Office == 0], df_test.Delivery_time[df_test.Office == 0])
plt.legend(['В офис', 'На дом'])
plt.xlabel('Время поступления заказа (Order_time_sec)')
plt.ylabel('Время доставки заказа (Delivery_time)')
plt.plot([82000, 82000], [0,10], 'red')
plt.plot([82000, 86400], [10,10], 'red')
plt.title('Тестовая выборка, принадлежность к классам')

На графиках мы видим одну и ту же область, где представители одного класса предсказываются неверно как на обучающей, так и на тестовой выборке. Попробуем исправить это!

Создадим новый столбец Order_time_sec_delta, который отличается от столбца Order_time_sec константой. В столбце Order_time_sec отметки времени расположены так, что последний заказ "на дом" (Office = 0) оказывается на отметке 86399 секунд от начала дня (т.е. ровно через сутки после начала). В Order_time_sec_delta время всех заказов «сдвинуто» циклично влево, ближе к началу дня, на дельту, равную разнице [24 часа - максимальное время заказа на дом во всем датасете].

def time_change(df):
    max_time_delivery=df.query("Office==0").Order_time_sec.max()
    delta = 24*60*60-max_time_delivery-1
    df['Order_time_sec_delta']=df['Order_time_sec']+delta
    df['Order_time_sec_delta']=df.Order_time_sec_delta.apply(lambda x: x - 86400 if x > 86400 else x)
    return(df)
df2 = time_change(df)

Для упрощения кода напишем функцию log_reg(y, X), которая принимает на вход целевой признак y и столбцы датафрейма X, представляющие собой признаки. Функция возвращает обученные объекты sc и lr.

def log_reg(y,X):
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=21)
    					
    sc = StandardScaler()
    sc=sc.fit(X_train) 
    
    X_train_std = sc.transform(X_train)              
    X_test_std = sc.transform(X_test) 
    
    lr = LogisticRegression(random_state=21)
    lr=lr.fit(X_train_std, y_train)
    
    return (sc, lr)

Строим классификатор №2.1, который отличается от классификатора №1, - только тем, что время заказа «сдвинуто».

df2=time_change(df)
y2 = 'Office'
x2 = ['Order_time_sec_delta', 'Delivery_time']
sc_delta, lr_delta = log_reg(df2[y], df2[x])
df_train2 = Processing_results(sc_delta, lr_delta, df2, y2, x2, 'delta')
df_train2

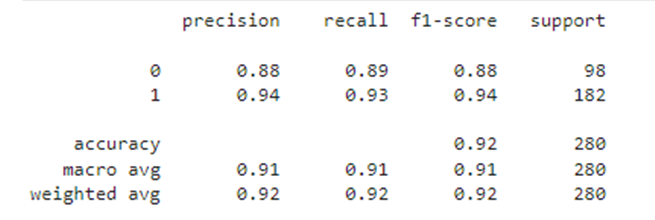
df_t2=time_change(df_test)
df_test2 = Processing_results(sc_delta, lr_delta, df2, y2, x2, 'delta', [x])
df_test2

Метрики доказывают, что качество классификатора улучшено. Это произошло за счет обеспечения монотонности целевой переменной от признаков, т.е. теперь выполняются правила:

• чем больше момент времени поступления заказа, тем выше вероятность доставки на дом;

• чем выше время доставки, тем выше вероятность доставки на дом.

К сожалению, не всегда есть возможность обеспечить монотонность целевой переменной от признаков без применения каких-нибудь дополнительных инструментов.

Еще одним способом улучшения классификатора является увеличение порядка пространства признаков, например, если на плоскости достаточно тяжело провести линию, разделяющую классы, то в трехмерном пространстве уже можно найти плоскость, которая сделает это лучше.

Все моменты времени преобразуем через синус и косинус, формируя тем самым вместо одного два признака. Это становится тем более важным, если у нас вместо одного временного периода имеется несколько и существует возможность периодических колебаний.

Преобразования производятся по следующим формулам:

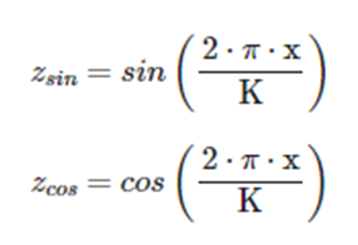
Здесь х - это значение момента времени, а К - значение временного периода в единицах измерения моментов времени. Например:

• если моменты времени измеряются в секундах, а временной период равен суткам, то К=86400;

• если моменты времени измеряются в днях, а временной период равен неделе, то К=7.

Проведем преобразование времени поступления заказа:

df['Order_sin'] = np.sin(df.Order_time_sec*math.pi/43200)
df['Order_cos'] = np.cos(df.Order_time_sec*math.pi/43200)

Построим графики целевого показателя в пространстве полученных признаков:

plt.scatter(df.Order_sin[df.Office == 1], df.Order_cos[df.Office == 1], color = 'red')
plt.scatter(df.Order_sin[df.Office == 0], df.Order_cos[df.Office == 0])
plt.legend(['В офис', 'На дом'])
plt.xlabel('Синус времени заказа')
plt.ylabel('Косинус времени заказа')
plt.show()

sns.scatterplot(x = 'Order_sin', y = 'Order_cos', data = df, hue = 'Office')
plt.show()

Построим классификатор №2.2.

y = df.Office
X = df[['Order_sin', 'Order_cos', 'Delivery_time']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=21)

sc_2 = StandardScaler()
sc_2.fit(X_train)
X_train_std = sc_2.transform(X_train)
X_test_std = sc_2.transform(X_test)

lr_2 = LogisticRegression(random_state=21)
lr_2.fit(X_train_std, y_train)

y_pred_2 = lr_2.predict(X_test_std)

#print(classification_report(y_test, y_pred_2))

y = 'Office'
X = ['Order_sin', 'Order_cos', 'Delivery_time']
df_train3 = Processing_results(sc_2, lr_2, df, y, X, '2')
df_train3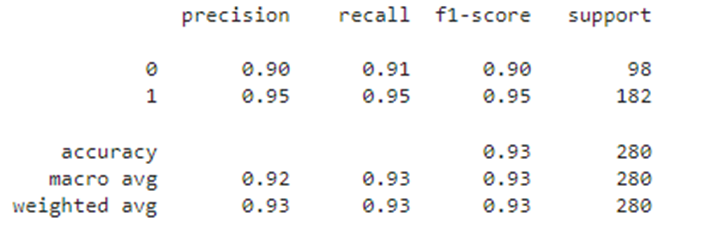

df_t3=time_change(df_test)
df_t3['Order_sin'] = np.sin(df.Order_time_sec*math.pi/43200)
df_t3['Order_cos'] = np.cos(df.Order_time_sec*math.pi/43200)
y3 = 'Office'
X3 = ['Order_sin', 'Order_cos', 'Delivery_time']
df_test3 = Processing_results(sc_2, lr_2, df, y3, X3, '3')
df_test3

Значение метрик еще увеличилось.

Теперь возьмем данные со смещенным временем, произведем преобразование через синус и косинус, построим классификатор №3 и сравним результаты.

df['Order_sin_new'] = np.sin(df.Order_time_sec_delta*math.pi/43200)
df['Order_cos_new'] = np.cos(df.Order_time_sec_delta*math.pi/43200)

y = df.Office
X = df[['Order_sin_new', 'Order_cos_new', 'Delivery_time']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=21)

sc_3 = StandardScaler()
sc_3.fit(X_train)
X_train_std = sc_3.transform(X_train)
X_test_std = sc_3.transform(X_test)

lr_3 = LogisticRegression(random_state=21)
lr_3.fit(X_train_std, y_train)

y_pred_3 = lr_3.predict(X_test_std)

y = 'Office'
X = ['Order_sin_new', 'Order_cos_new', 'Delivery_time']
df_train4 = Processing_results(sc_3, lr_3, df, y, X, '3')
df_train4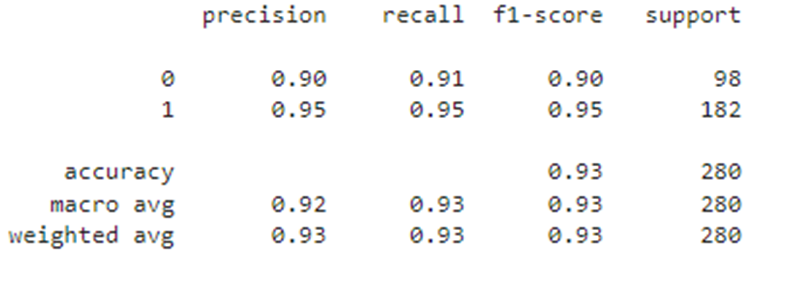

df_t4=time_change(df_test)
df_t4['Order_sin_new'] = np.sin(df_test.Order_time_sec_delta*math.pi/43200)
df_t4['Order_cos_new'] = np.cos(df_test.Order_time_sec_delta*math.pi/43200)

y4 = 'Office'
X4 = ['Order_sin_new', 'Order_cos_new', 'Delivery_time']
df_test4 = Processing_results(sc_3, lr_3, df_t4, y4, X4, '4')
df_test4

Мы рассмотрели, как можно работать с имеющимися данными, чтобы улучшить метрики классификатора. Результаты последнего классификатора на тестовой выборке оказались самыми высокими. На практике обеспечение монотонности целевой переменной от признаков, а также увеличение порядка пространства признаков чаще всего приводит к улучшению метрик классификатора и улучшению обучаемости модели.

Таблица 1 Метрика Accuracy в разных моделях.

P. S. Датасеты можно скачать здесь: ссылка на Github.