Вступление

Когда мы расставляем мебель в комнате, мы ориентируемся на габаритные размеры мебели и фурнитуры, а не на их занимаемую площадь, и мебель часто квадратной формы. С полигонами на карте дело обстоит немного иначе, они могут быть произвольной формы, но должны иметь определенную площадь, а задача такая же как и с мебелью - уместить всё в комнату (участок). Когда полигоны квадратные, то рассчитать нужное изменение длины ребра для получение желаемой площади, не так и сложно. С полигонами сложной формы всё не так просто, но и это тоже не проблема, ведь можно методом тыка подобрать нужную площадь. Проблема возникает когда количество полигонов возрастает. Пример: на изменение полигона сложной формы уходит 5 минут (грубо говоря), но нам нужно изменить 15 полигонов, считаем и получаем 75 минут. За 75 минут можно сделать гору полезных дел, а всего было отредактировано 15 полигонов. Если полигоны придется менять заново? вдруг нужно их будет разбить на другую площадь? Вот была бы такая программа, которая сама бы изменяла полигон и добавляла бы нужную площадь.

Алгоритм для скейла полигонов

Тут я решился создать такую программу и выбрал для этого Python, так как это очень удобный язык программирования. Первая проблема с которой я столкнулся - это написание алгоритма. Нельзя пока поставить задачу компьютеру как человеку одним предложением и просто подождать пока он решит и выдаст тебе готовый ответ. Поэтому я приступил к самому трудному, описанию алгоритма.

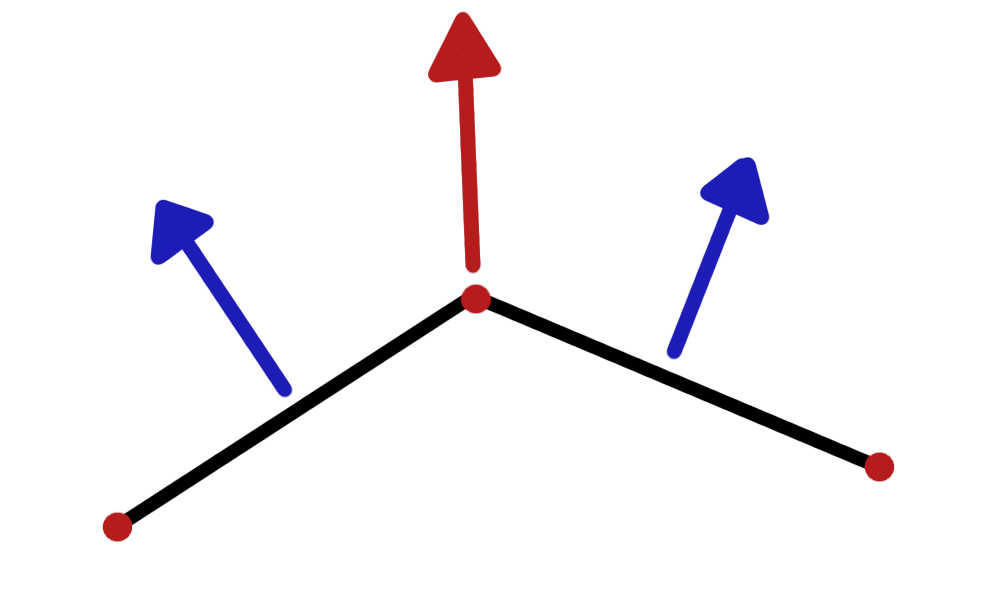
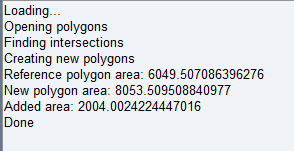
Было бы здорово и классно, если бы полигоны не пересекались и были бы не окружены другими полигонами. Можно было бы просто рассчитать нужный скейл для полигона и всё решено. Когда полигон что-то окружает, то всегда найдется область в которой полигон по хорошему не должен находится. Пример: участок дома в виде полигона не должен быть в реке или на трассе, к сожалению. Поэтому сначала алгоритм решает задачу нахождение границы  пересечения. Это не сложно, граница находится сравниванием координат точек одного полигона с другим. Теперь нам нужно сдвинуть точки пересечения (первого со вторым полигоном) в сторону второго полигона. На помощь нам приходят вектора, они как раз и сдвинут точки в сторону второго полигона. Тут есть первая трудность - это построение вектора для определенной точки полигона. Первый способ который мне пришел на ум - это использовать нормали ребер окружающих нашу выбранную точку рис. 1. Мы их суммируем и получаем нужный нам вектор трансформации (красный вектор на рис. 1). Метод вроде бы рабочий, но есть большая проблема. Как определить в какую сторону должен смотреть вектор ребра? Пытаясь решить эту проблему я нашел другой способ создания вектора трансформации. Зачем всё усложнять и использовать сложение векторов, если можно построить сразу вектор трансформации. Для построения  вектора нужна разность координат двух точек.

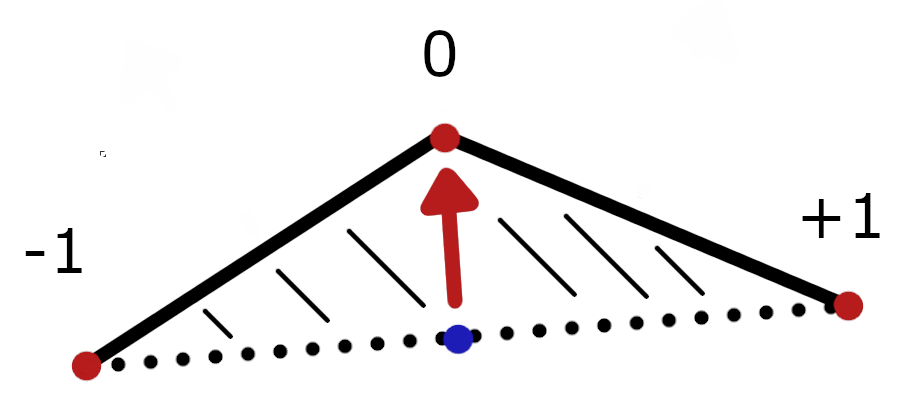
Одна точка у нас есть, точка пересечения первого полигона со вторым. Нам нужна вторая точка. Эта точка будет средней точкой между точками с индексами -1 и +1 рис. 2. Теперь мы сможем всегда направлять вектор в нужную нам сторону, просто проверяя принадлежит ли средняя точка полигону или нет. Не дай бог, в полигоне будет отверстие и средняя точка попадет туда, тогда ваш полигон схлопнется. Эту проблему решим позже.

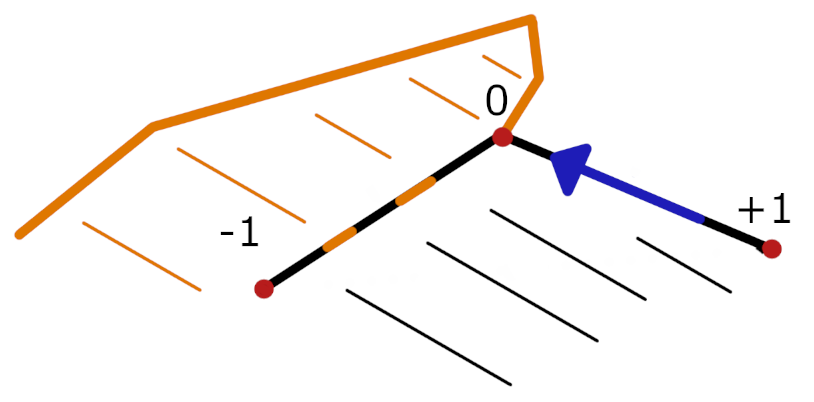
Настало время написание кода и тестирование программы. Использовал я несколько библиотек. Первая это Shapely, позволяет создавать точки, ребра и полигоны. Есть множество полезных функций для работы с геометрией. Для визуализации наших полигонов нам поможет библиотека MatPlotLib. Она позволяет визуализировать точки, полигоны, линии, графики и много чего другого. Визуализация нужна для отладки кода и понимания что программа делает всё корректно, иначе по координатам очень сложно понять результат работ. Для удобства загрузки данных нужен простой интерфейс. В этом нам поможет библиотека PySimpleGUI. В ней есть все необходимое для создания кнопок, строк, канвасов и тд.

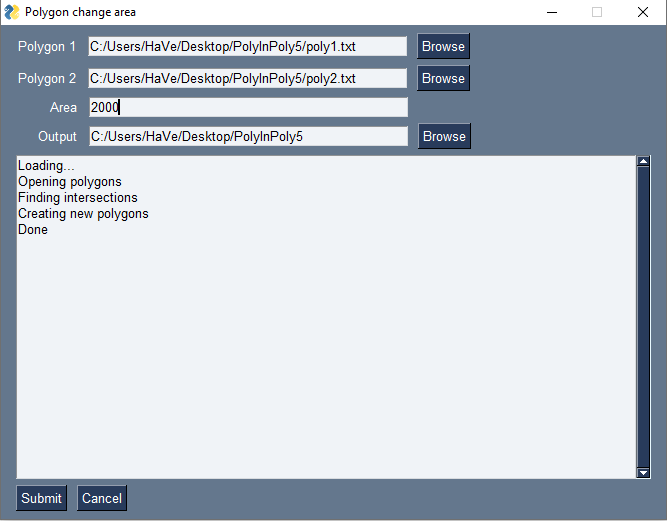
Первая версия программы была написана и конвертирована в “exe” файл рис. 4. Для получения двух новых wkt файлов необходимо выбрать два полигона, указать нужную площадь в метрах квадратных и папку вывода рис. 4. После нажатия кнопки “Submit”, если всё хорошо, выводится два файла и пишется слово “Done” рис. 4. Первая версия, хоть и работала, но не показывала результат, а это не удобно. Следующая версия рассчитывала и выводила прибавленную площадь рис. 5.

Тут и появилась первая проблема. Если не нормализовать каждый вектор, то теряется точность. Поэтому каждый вектор теперь нормализуется. Но и тут проблема не ушла, точность ухудшается в зависимости от размера прибавленной площади. Чем прибавленная площадь ближе к площади исходного полигона, тем сильнее погрешность. Эту проблему сначала я решил не самым лучшим способом. Я поставил диапазоны для значение “Area”, относительно его подобрал нужный множитель для векторов, чтобы вручную скорректировать точность. Как можно догадаться это работало только на одном наборе данных, поэтому костыли это плохо.

Следом после этого вылезла ещё одна проблема. Все вогнутости полигона, при сильном масштабировании, обязательно пересекутся сами с собой рис. 6.

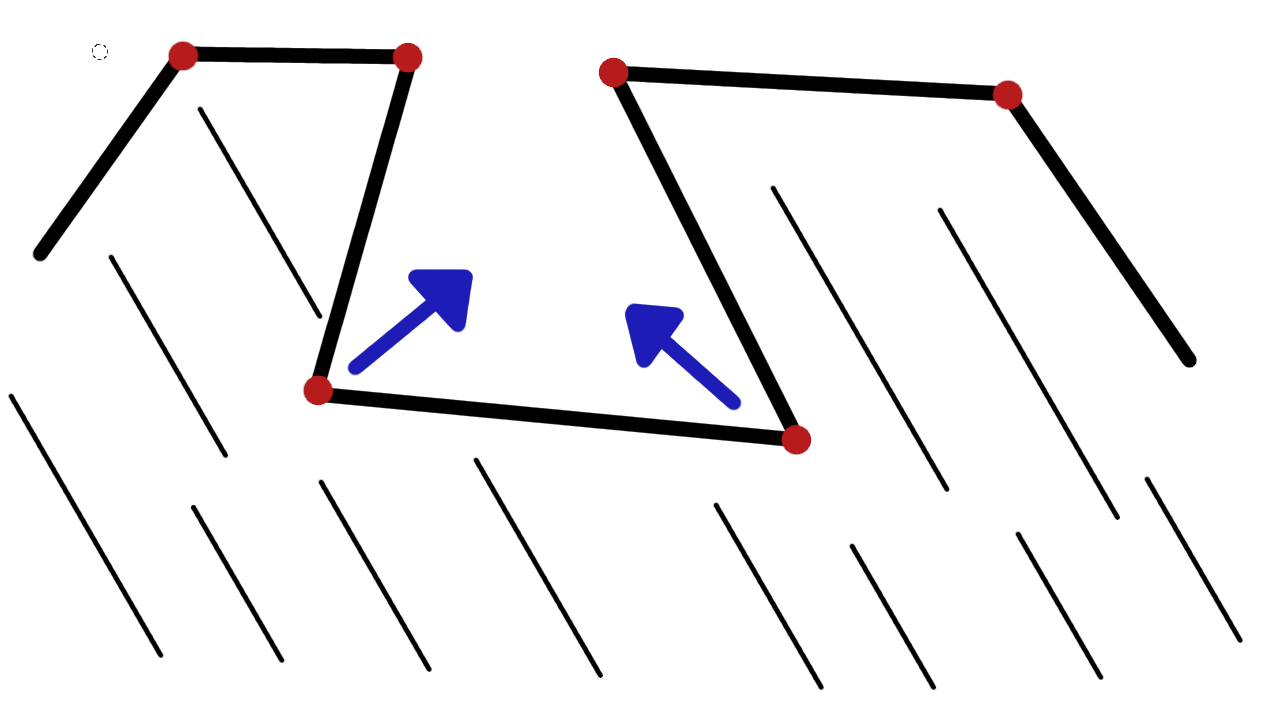
Не будем паниковать и вспомним как работает наша программа. Вектора создаются только к точкам пересечения, если вогнутость полигона исчезнет, никто жаловаться не будет. Поэтому я дописал код, он начал удалять все точки, которые описывают вогнутость полигона. Для нахождения этих точек я использовал алгоритм со средней точкой, описанный выше. Теперь о проблеме с отверстиями по середине, когда средняя точка попадает в отверстие в центре полигона. Программа считает внешний угол за внутренний и убирает его. Решается очень просто, вектор сначала всегда разворачивается и создается новая точка от исходной точки. ref point + vector = новая точка. Теперь проверяется, лежит ли эта новая точка в полигоне или нет. Мы приблизили среднюю точку к исходной, чтобы не попадать в отверстие при проверке. Также была решена проблема с несколькими точками на одном ребре. Между точками с индексами -1 и +1 создается ребро, и к этому ребру применяется buffer. Программа проверяет, лежит ли точка с индексом 0 в полигоне, созданного от ребра функцией buffer. На рис. 7 изображен результат работы программы.

Синий полигон - исходный, оранжевый полигон - второй полигон рис. 7. Красный контур это полигон, который создается в результате “магии” первого полигона со вторым. На рисунке 7 заметно, что красный контур не имеет вогнутых поверхностей на территории второго полигона.

Программа работает на этих двух полигонах превосходно, но не всегда будут эти объекты. Попробуем другие полигоны. Тут нас встречает другая проблема, связанная с методом построения наших полигонов. Так как для построения вектора берется средняя точка между -1 и +1 и иногда длина ребер сильно разная. Взгляните на рис. 8 и вы поймете, что вектора в редких случаях снова пересекаются. Всё не так плачевно и не нужно переписывать всю программу заново. Воспользуемся функцией Convex hull и всё починится. Единственное нужно чтобы функция применялась не ко всем точкам, иначе полигон может изменится там где это не нужно. Поэтому применяем Convex hull и отрицательный buffer. Прогоняем каждую точку, и та которая лежит в уменьшенном полигоне убирается. Добавляем условие, точка должна пересекаться со вторым полигоном. Теперь convex hull применяется только к нужным точкам.

Давайте теперь проверим программу. На рис. 9 красный контур имеет всего 4 вершины и очень приятную форму.

Осталось теперь добавить еще одну коррекцию длины векторов после всех оптимизаций, иначе будет приблизительно потеря точности 30%. Почитав пару гайдов в интернете по интеграции matplotlib в PySimpleGUI, получаем канвас прямо в окне PySimpleGUI. На рис. 10 новый интерфейс.

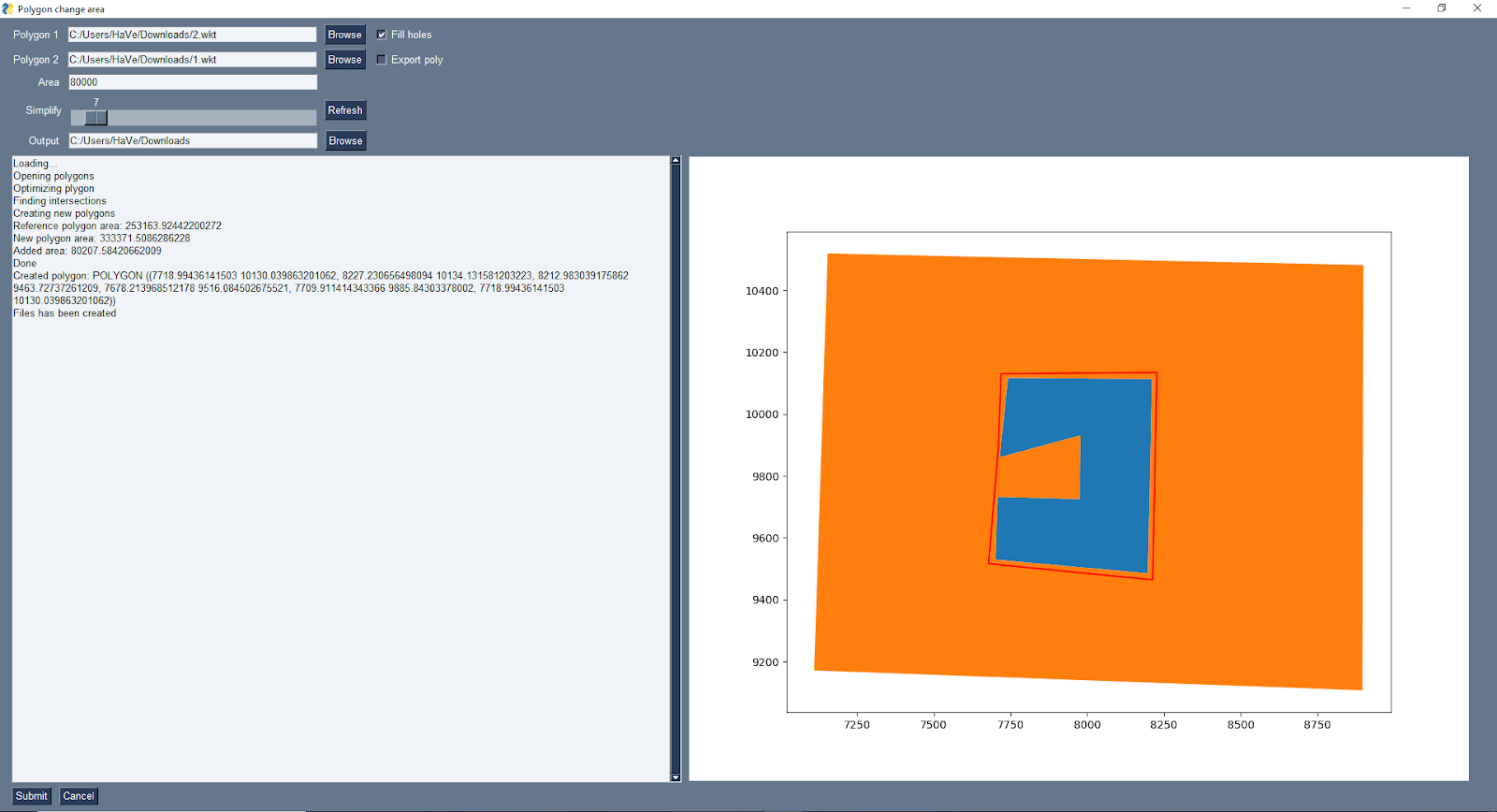
Программа имеет пару острых углов, но уже работает и выполняет свою основную задачу. Если нужен новый второй полигон, то поможет булева операция “Difference”. Буду очень рад за любые комментарии и советы по поводу улучшения программы. Код можете посмотреть на GitHub: https://github.com/Geomanti/PolyInPoly

Вывод

Костыли это плохо и все равно потом придется их переделывать. Чем больше тестовых данных тем лучше. Для удобства отладки нужно всё визуализировать и чем ярче тем лучше. Улучшать программу можно очень долго, но не всегда в этом есть нужда. Ушло 20 часов на написание алгоритма и кода в Python, изучение библиотек и туториалов.

Список использованной литературы

1. Документация к библиотеке Shapely

2. Пример создания полигона в MatPlotLib

3. Интеграция MatPlotLib в PySimpleGUI

4. Документация к библиотеке PySimpleGUI

5. Учебник русского языка