Появилась у меня с маленьким ребенком новая красивая настолка - классическая ходилка с одним кубиком. Симпатичная картинка, достаточная длина игровой сессии. И есть в этой игре странная особенность - чёрная дыра на 39 шаге (из 120), которая сразу отбрасывает игрока в самое начало. Давайте посчитаем насколько это сТранно. И мелкий совет в конце по расширению правил для возможного исправления.
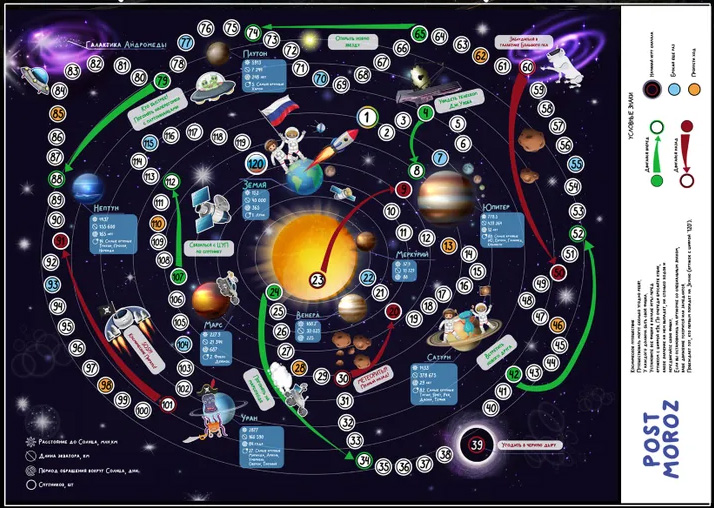
В чем проблема?
У игрока нет никакого контроля и возможности повлиять на результат. То есть победа или поражение - полная случайность. Поэтому если уж не повезло попасть на черную дыру, то догнать оппонента почти нереально, ведь это одна треть всего маршрута.
В игре нет никакой механики камбека. Более того всегда есть заметная вероятность второй раз попасть на черную дыру. Уныние у такого игрока обеспечено.
Насколько проблема большая?
С ходу может показаться, что риск такого события всего лишь ~17% (1/6 для шестигранного кубика). Вроде терпимо. Но если подумать ещё, то окажется, что проверять надо не одного игрока, а двух, т.к. нас интересует интересность в игре обоих игроков. Ещё хуже если игроков больше двух. Но можно подумать ещё, и тогда окажется, что для одного игрока опасных бросков не один, а обычно больше (2, иногда 3). Например, игрок находится на расстоянии 6 от чёрной дыры, выпадает 2 и он вздыхает с облегчением, но зря, т.к. на следующий свой ход он опять в той же ситуации и фатальной для него теперь является четвёрка.
Рассчитать вероятность всего этого через теорию вероятности несколько проблематично. Зато можно заэмулировать и просто собрать статистику.
const bonusTurn = [7, 22, 55, 70, 77, 93, 104, 115];
const skipTurn = [13, 28, 46, 62, 85, 98, 110];
function main(gamesCount) {
let games = [];
for (i = 0; i < gamesCount; i++) {
games[i] = emulateGame();
}
//console.log(games);
let catchedGames = 0;
let catchedGamesUnfair = 0;
let catchedMoreLoseGames = 0;
for (i = 0; i < gamesCount; i++) {
if (games[i].p1Catched > 0 || games[i].p2Catched > 0) {
catchedGames++;
if (games[i].p1Catched != games[i].p2Catched) {
catchedGamesUnfair++;
}
}
if (games[i].p1Catched > games[i].p2Catched && games[i].winner == 'p2') {
catchedMoreLoseGames++;
} else if (games[i].p1Catched < games[i].p2Catched && games[i].winner == 'p1') {
catchedMoreLoseGames++;
}
}
console.log('Count of games: ' + gamesCount);
console.log('Percent of games with black hole: ' + Math.round(100*catchedGames/gamesCount) + '%');
console.log('Percent of unfair games with black hole: ' + Math.round(100*catchedGamesUnfair/gamesCount) + '%');
console.log('If go to black hole more then lose: ' + Math.round(100*catchedMoreLoseGames/catchedGamesUnfair) + '%');
}
function emulateGame() {
let game = {
'p1': 0,
'p2': 0,
'winner': null,
'p1Catched': 0,
'p2Catched': 0,
'turn': 0
}
while(true) {
game.turn++;
game.p1 += getDice();
game = checkMove(game, 'p1');
if (game.p1 >= 120) {
game.winner = 'p1';
break;
}
game.p2 += getDice();
game = checkMove(game, 'p2');
if (game.p2 >= 120) {
game.winner = 'p2';
break;
}
}
return game;
}
function checkMove(game, player) {
let anotherPlayer = 'p1';
if (player == anotherPlayer) {
anotherPlayer = 'p2';
}
if (bonusTurn.indexOf(game[player]) !== -1) {
game[player] += getDice();
game = checkMove(game, player);
}
if (skipTurn.indexOf(game[player]) !== -1) {
game[anotherPlayer] += getDice();
game = checkMove(game, anotherPlayer);
}
if (game[player] == 39) {
game[player] = 0;
game[player + 'Catched']++;
}
if (game[player] == 4) {
game[player] = 8;
}
if (game[player] == 23) {
game[player] = 9;
}
if (game[player] == 24) {
game[player] = 34;
}
if (game[player] == 30) {
game[player] = 20;
}
if (game[player] == 42) {
game[player] = 52;
}
if (game[player] == 60) {
game[player] = 50;
}
if (game[player] == 65) {
game[player] = 74;
}
if (game[player] == 79) {
game[player] = 88;
}
if (game[player] == 101) {
game[player] = 91;
}
if (game[player] == 107) {
game[player] = 112;
}
return game;
}
function getDice() {
return Math.floor(Math.random() * 6 + 1);
}
main(1000000);
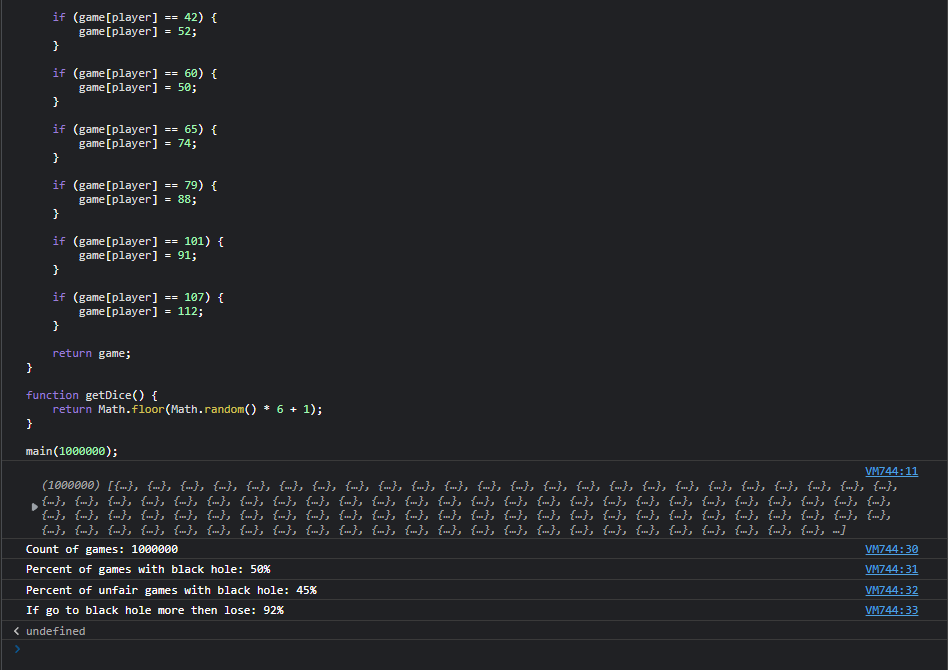
Итого, при эмуляции одного миллиона игр мы получаем такую статистику:
Вероятность того, что хоть кто-нибудь хотя бы раз попадет в черную дыру: 50% (!!!);
Вероятность того, что игра будет несправедливой, когда у кого-то будет больше попаданий в черную дыру, чем у оппонента: 45%;
Вероятность того, что игрок с большим попаданием в чёрную дыру проиграет: 92%.
А что можно сделать?
Самый примитивный вариант: игнорировать чёрную дыру или считать её за обычный пропуск хода.
Вариант посложнее: каждому игроку дать по две фишки, чтобы была возможность выбора, кем передвигаться. В этом случае игра превращается из простого рандома в чуть более тактическую игру. И ребёнку гораздо полезнее, когда он не просто тренируется соблюдать игровые правила, но и учится играм с контролем.
Заключение
Вероятность попадания в черную дыру на 50% меня весьма удивила, я ожидал поменьше. Не менее удивительны целых 8% победы даже в случае чёрной дыры. Вот они когнитивные искажения.
А вот гейм-дизайнерам, я считаю, нужно всё же тестировать свои собственные игры получше. Анализ "на глазок" может подложить подобную свинью. Данная механика приносит почти всегда только разочарование и 8% на "победу вопреки" того не стоит. Особенно в игре, где это "вопреки" происходит исключительно по воле случая.
Комментарии (40)

GrueneGespenst
20.12.2022 09:27+2Есть еще игра "Вокруг света": там со 107 хода из 120 отбрасывает на 37


mSnus
20.12.2022 09:38+2Аааа, где бы её купить или распечатать?

datacompboy
20.12.2022 10:49+1Вот это как раз даёт шанс что если тебя обогнали - ты можешь надеяться на их отлет взад...

vesper-bot
20.12.2022 12:20+2Была у меня игра про Незнайку, там 80 полей, с 31 на 71 улетали, но с 72 на 33 и с 73 на 42. При этом можно было улететь назад не раз и не два… собственно, как и здесь. Так что такие перелеты взад-вперед были когда-то нормой.
Нашел тут http://samoe-vazhnoe.blogspot.com/2017/09/priklucheniya-neznayki.html но сайт картинки не отдает (платформа матьиво).

Scootaloo
20.12.2022 09:41+5Зачем играть с ребёнком в бродилки где у игроков отсутствует какой-либо контроль? На рынке ведь сотни и тысячи настольных игр самых разных направленностей на любой бюджет от самых привычных и попсоватых - уно, имаджинариумы и прочие, мимо интересных, но всё ещё не сложных, вроде каркассона (или, например, попадалась мне игра где нужно строить из ажурных деталек многоэтажный город по несложным правилам, красиво, осязабельно, понятно) и кончая древними ужасами.
Найти в этом многообразии игру которая зайдёт ребёнку хоть пяти, хоть двенадцати лет совершенно нетрудно
Metotron0
20.12.2022 23:20Каркассон с несколькими дополнениями — это уже три часа игры на 4 игроков, где нужно планировать тележку/строителя/башню/мэра/амбар/свинью, ещё и от дракона страдать, и принцессу туда-сюда мотать, и не забывать следить, чтобы капища рядом с монастырями не стояли, а ещё помнить про собор, или как его там, который встаёт в любое пересечение полей, и передавать фишки разбойника и короля… Становится не чересчур легче Проекта Гайя.

IntActment
21.12.2022 08:00Тоже заводил себе правило: играть только с несколькими дополнениями. Помимо возрастающей сложности и увеличения длительности игры, при росте числа карточек баланс сильно смещается в пользу захвата полей. Пробовал играть двойным набором - вот там это было сильно заметно

mSnus
20.12.2022 09:41+2По механике:
Хардкор это классно
Если не нравится совсем хардкор, можно добавить на черной дыры "saving throw" - например, если выпало 1-5, то просто отбрасывает на 1-5 назад, а если уж 6 - значит ты неудачник
Какова вероятность, что из 5 игроков за игровую партию в дыру попадёт только один?

qnok Автор
20.12.2022 10:21Мы это решали игрой двумя фишками и броском трех кубиков для ускорения игровой сессии

Nikita_64
20.12.2022 13:05Бросок нескольких кубиков полезен дошкольникам (и не только) тем, что они быстрее учатся считать. Мой сын начал в 4 года с двух, а в 5 лет вошел во вкус и играл 5-6 кубиками, комбинируя выпавшие очки в десятки.

mokhin-denis
20.12.2022 09:48+1Если ребенок совсем малой, попробуйте Monopoly Junior. Если старше, то хотя бы Вокруг света за 80 дней.

qnok Автор
20.12.2022 10:026 лет

mokhin-denis
21.12.2022 08:28+1В этом возрасте мы шли от обратного. Ребятня сама рисовала себе ходилки, как хотела. И правила назначала сама. И мы вместе играли.

Shkaff
20.12.2022 11:01+1У нас тоже есть эта игра, просто ужасно. Мы сыграли пару раз, ребенку было норм, а меня бесило до жути. Хорошо, что это всего одна игра из 40+ детских в коллекции и ее можно просто
выброситьотложить на полку xD

Alexandroppolus
20.12.2022 11:26+1У меня в детстве была офигительная карта "Цирк", с двумя драматичнейшими мувами вверх и вниз. Загуглить так и не удалось.. Ещё была карта по мотивам сказок, там одного большого падения нет, но если сильно "повезет", можно было тремя неудачными попаданиями отлететь с предпоследней позиции почти до старта.

ReinRaus
20.12.2022 11:46+1Можно добавить правило: после попадания в чёрную дыру игрок получает "гипер-ускорение" и каждый его бросок получает +1 к выпавшему значению на кубике (или +2, +3 - необходимо экспериментально настроить правило для баланса).

spag002
20.12.2022 11:49Рассчитать вероятность всего этого через теорию вероятности несколько проблематично.
В данном случае это делается довольно легко, хоть и брутфорсом.
Суть задачи: найти и сложить все вероятности, когда сумма очков за все ходы подряд равна 39. Т.е. N1 + N2 + ... + Nn = 39, где вероятность самого Nn = 1/6.
Если: 1 + 1 + ... + 1 = 39, то P = 1/6 ^ 39. Если: 2 + 1 + ... + 1 = 39, P = 1/6 ^ 38. И т.д.
P = P1 + P2 + ... + Pn.
В общем, я сильно сомневаюсь насчет 50%.

qnok Автор
20.12.2022 11:53С моей колокольни выглядит так, что быстрее написать js скрипт. Это же практическая задача, а не научная.

Alexandroppolus
20.12.2022 11:58+1найти и сложить все вероятности, когда сумма очков за все ходы подряд равна 39
Это без учета двух красных и зеленых стрелок до черной дыры. С ними всё чуть хитрее, красные стрелки вообще вылезут в убывающую геометрическую прогрессию.

Alexandroppolus
20.12.2022 12:54Без стрелок, кстати, вероятность попасть в черную дыру очень просто вычисляется через рекурсию с мемоизацией:
P(n) = 1/6 * (P(n-1) + P(n-2) + ... + P(n-6))
Где n - количество шагов до черной дыры. P(0) = 1, P(<0) = 0.
Наверно, это и к стрелкам можно как-то прикрутить..

vedenin1980
20.12.2022 13:33+1Вариант посложнее: каждому игроку дать по две фишки, чтобы была возможность выбора, кем передвигаться. В этом случае игра превращается из простого рандома в чуть более тактическую игру. И ребёнку гораздо полезнее, когда он не просто тренируется соблюдать игровые правила, но и учится играм с контролем.
Простейшая логика говорит, что в этом случае выиграшная стратегия — всегда ходить одной фишкой, кроме случая когда следующим ходов попадаешь в ЧД — тогда нужно пойти второй фишкой.
Вообще, в таких случаях мы добавляли правило, что на финальную точку можно придти выкинув точное число на кубике, если выкидываешь больше — либо пропускаешь ход (то есть в второго игрока есть шанс догнать), либо начинаешь круг заново (это более хардкорно, но игра может затянуться).

Rsa97
20.12.2022 13:55+1Накидал аналогичную программку на PHP, получил на миллионе игр двух игроков следующее:
Вероятность попасть в чёрную дыру для конкретного игрока 0 раз за игру — 70.6%, 1 раз — 21.5%, 2 — 6.5%, 3 — 1.3%, 4 — 0.17%, 5 — 0.02%, 6 — 0.017%, 7 — 0.0004%
Вероятность, что хоть один игрок за игру попадёт в чёрную дыру — 50%
Игр с попаданием в чёрную дыру равное количество раз обоими игроками — 55%
Вероятность выигрыша игрока, который больше раз попадал в чёрную дыру — 4%
Вероятность выигрыша первого игрока — 51.5%
qnok Автор
20.12.2022 14:07Отличие похоже только в этом
"Вероятность выигрыша игрока, который больше раз попадал в чёрную дыру — 4% "
Но похоже из-за того, что я этот параметр рассчитывал делением на число попаданий в черную дыру, а не на общее число игр.



qnok Автор
Кстати, у первого игрока тут 52% вероятности выиграть просто за счет права первого хода.
AlexWork22
Целых 2 процента преимущества, весомая цифра
Mirzapch
4% преимущества, если быть точным.
AlexWork22
Подскажите как считаете? В Покере например на чемпионатах показывают шанс победы, к примеру 60% и 40%, что демонстрирует разницу в 20% = на 20% больше вероятности победы первого игрока. Или я неправильно смотрел покер?
Squoworode
Всё правильно. У одного больше половины, у другого - на столько же меньше.
В покере 60% для двух игроков даёт (10%)×2 =20% разницы.
Здесь у первого 52%, соответственно, у второго - 48%.
Arcanum_Viator
Если шанс победить равен 52%, то шанс победы конкурента 48%. 52-48=4.