22.01.2023 01:51
interesting-cs-math 0 745 Источник

Пусть имеется множество X.

Определение. Группа G действует на множестве X, если \forall g \in Gи \forall x \in Xопределено действие элемента g на элемент x (обозначаемое gx), обладающее следующими свойствами:

  1. gx \in X;

  2. \forall {g}_{1}, {g}_{2} \in G, \forall x \in Xвыполнено ({g}_{1}{g}_{2})x = {g}_{1} ({g}_{2}x);

  3. \forall x \in Xвыполнено ex = x.

Пример 1. X = \mathbb {R}^{2}, G = \{ \mathbb{R} \setminus \{ 0 \}, \cdot \}.

Для элементов (x,y) \in X:g(x,y) = (gx, gy),где g- действие, (gx,gy) \in \mathbb{R}{^2}.

Пример 2. Композиция действий z = sin(ln(x)).

Композиция действий
Композиция действий

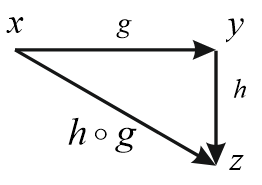
Пример 3. Поворот вектора (x,y)на угол \alpha против часовой стрелкиG = \{ [0, 2\pi), + \text{ mod} 2\pi \}.

Пример 4. X = \mathbb{B}^{n}(упорядоченные наборы из нулей и единиц длиной n).

Группа перестановок G = {S}_{n}с операцией композиции.

p = ({p}_{1}, {p}_{2}, \ldots, {p}_{n}) \in {S}_{n}.

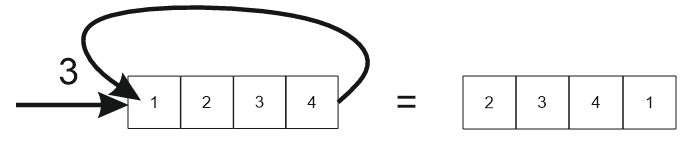
Пример 5. ПустьX = {T}^{n}(упорядоченные числовые наборы - массивы чисел), группа циклических сдвиговG = \{ \{ 0, \ldots, n-1 \}, + \text{ } mod \text{ } n \}.

Обратный элемент к элементу a \in G вычисляется следующим образом: {a}^{-1} = (n-a) \text{ } mod \text{ } n.

Циклический сдвиг массива на 3 позиции вправо
Циклический сдвиг массива на 3 позиции вправо

Классы эквивалентности (орбиты)

Определение. Пусть группа Gдействует на множество X.Тогда орбитой элемента x \in Xназывается множество: Orb(x)=\{y∈X∣∃g∈G:g⋅x=y\}.Множество всех орбит обозначается так:X/G.

Пример 1. Множество X- числовые массивы длиной n. G- группа перестановок длины n.X = {T}^{n},G ={S}_{n}.

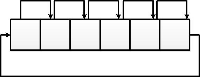
В данной перестановке существует единственный класс эквивалентности.
В данной перестановке существует единственный класс эквивалентности.

Пример 2. {T}^{n}: \{ 0, \ldots, n-1 \} + \text{ } mod(n)циклический сдвиг массива длиной n.

Пример 3. X = {A}^{k}_{n}- размещения из nпо k.G = {S}_{n}- перестановки nэлементов. Классами эквивалентности в данном случае будут сочетания из nпо k:X / G = {C}^{k}_{n}.

Пример 4. Группа поворотовG = \{ \alpha \in [0, 2\pi], + \text{ } mod (2\pi )\}действует на множествоX = {\mathbb{R}}^{2}. Орбитами (классами эквивалентности) в данном случае являются концентрические окружности.

Неподвижная точка

Определение. Пусть группа Gдействует на множество X.Неподвижной точкой для элемента gназывается такой элемент x,для которого gx = x.

Определение. Пусть конечная группа Gдействует на множестве X.Для элемента x ∈ Xего стабилизаторов (в группе G) называется подмножество элементов группы Gоставляющих его (элемент x) на месте.

Пример 1. Умножение координат точки в плоскости \mathbb{{R}^{2}}на константу.

g(x,y) = (gx, gy), x \in \mathbb{R}, y \in \mathbb{R}, (x,y) \in \mathbb{R}^{2}, (gx, gy) \in \mathbb{R}^2.

Если g = 1,то \forall (x,y) \in \mathbb{R}^2выполняется (x,y) = (gx, gy).

Если g \ne 1,то \exists! (x,y): (x,y) = (gx, gy).И эта точка (0,0).

\begin{equation*}\begin{cases} {St}_{g} = \{(0,0)\}, & g \ne 1; \\ {St}_{g} = {\mathbb{R}}^{2}, & g = 1. \end{cases} \end{equation*}

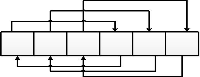
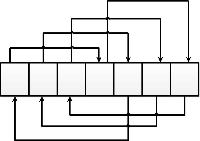
Пример 2. Рассмотрим массив, состоящий из 5 чисел и некоторую перестановку к нему:

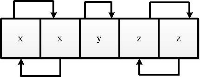
Как найти количество неподвижных точек у произвольной перестановки?

Перестановка разбивается на циклы.

В каждом цикле элементы должны быть равны (одинаковы).

Между циклами элементы могут соотноситься произвольным образом. Число циклов равно НОД(n,d).

n = 6, d = 3. НОД(6,3) = 3.
n = 6, d = 3. НОД(6,3) = 3.
n = 7, d = 3. НОД(7,3) = 1.
n = 7, d = 3. НОД(7,3) = 1.

Лемма Бернсайда

Теорема. Число орбит равно средней мощности стабилизатора элементов группы G.

X/G = \frac{\sum_{g \in g} |{St}_{g}|}{G}.

Пример. T = \mathbb{B}, n = 3.

000

001

010

100

110

101

011

111

123

000

001

010

100

110

101

011

111

132

000

010

001

100

101

110

011

111

213

000

010

100

010

110

011

101

111

312

000

100

001

010

011

110

101

111

231

000

010

100

001

011

011

110

111

321

000

100

010

001

011

101

110

111

\widetilde {X}

{x}_{1}

{x}_{2}

{x}_{3}

...

{x}_{i}

\ldots

{x}_{k}


{g}_{1}

{g}_{2}

{g}_{3}

\ldots

{g}_{j}

{g}_{j}{x}_{i}

\ldots

{g}_{n}

|G| \cdot |X / G| = \sum_{x \in X} |Stx| = \sum_{x \in X} \sum_{g \in G} [ gx = x ] = = \sum_{g \in G} \sum_{x \in X} [gx = x] = \sum_{g \in G} |{I}_{g}|.|X / G| = \frac{\sum_{g \in G} |{I}_{g}|}{|G|}.

Пример. Рассмотрим множество двоичных массивов длиной 3. n = 3, X = {\mathbb{B}}^{3}.

Группа G = {S}_{3}действует на множество X = {\mathbb{B}}^{3}.

Вычислим среднюю мощность стабилизатора элементов группы G.

\pi

|{I}_{\pi}|

123

8

132

4

213

4

231

2

312

2

321

4
\frac{8+4+4+2+2+4}{6} = 4.

По лемме Бернсайда число орбит (классов эквивалентности) равно 4.

Теорема Пойа

Теорема Пойа является обобщением леммы Бернсайда. Она также позволяет находить количество классов эквивалентности, но уже используя такую величину, как кол-во циклов в перестановке.

Пусть количество циклов в перестановке gравно C(g).

Количество цветов для раскрашивания бусин равно k.

Количество циклов равно С(g) = НОД(n,d).

Каждый цикл может быть окрашен в один из kцветов: {k}^{НОД(n,k)}.

По всем циклическим сдвигам: \sum_{d=0}^{n-1}.

Количество всевозможных циклических сдвигов равно n.

Количество ожерелий можно вычислить по формуле:

\frac{\sum_{d = 0}^{n-1} {k}^{НОД(n,d)}} {n}.

Пример. k = 3, n = 5.

Вычислим количество ожерелий по теореме Пойа:

d = 0: gcd(0,5) = 5,d = 1: gcd(1, 5) = 1,d = 2: gcd(2, 5) = 1,d = 3: gcd(3, 5) = 1,d = 4: gcd(4, 5) = 1.\frac{3^5 + 3 + 3 + 3 + 3}{5} = \frac{255}{5} = 51.

Аналогичный результат получаем по лемме Бернсайда:

|{St}_{0}| = 3^5, |{St}_{1}| = 3, |{St}_{2}| = 3, |{St}_{3}| = 3, |{St}_{4}| = 3. \frac{3^5 + 3 + 3 + 3 + 3}{5} = \frac{255}{5} = 51.

Комментарии (0)