Глубокие нейронные сети добились ошеломительного успеха во множестве областей и применений благодаря способности улавливать самые сложные и нетривиальные закономерности в данных. Однако, выдающиеся способности современных моделей сопровождаются существенными вычислительными затратами, что усложняет и ограничивает их применимость в прикладных задачах, поэтому огромное количества труда и усилий было потрачено на разработку разнообразных методов по сжатию сетей без значительной просадки в качестве - прунинга (структурированному и неструктурированному), квантизации, матричных и тензорных разложений, knowledge distillation и многих других. Тема сегодняшнего разговора будет наиболее близка по смыслу к неструктурированному прунингу - определению весов, которые можно выбросить из модели с минимальными негативными последствиями.
Дисклеймер
Дальнейшее повествование будет не сколько про практическую пользу и применимость в производстве, а про феноменологию.
На практике обычно берут предобученную сеть и прореживают ее, используя некоторый критерий важности весов, с дообучением спарсифицированной модели или без (в отсутствие достаточного количества ресурсов). Существуют и процедуры разреженного обучения модели с нуля, когда модель поддерживается постоянно в разреженном состоянии, но выбор зануленных весов может меняться с течением времени.
Может возникнуть вопрос - если существует избыточность в количестве параметров, то почему бы просто не взять модель поменьше?
Как показывает опыт, размер имеет значение, и во многих задачах меньшие сетки не способны воспроизвести качество своих больших собратьев. По всей видимости, причина явления лежит в оптимизации. Большие модели обладают большей гибкостью и потенциалом в возможности подстроить оптимальным образом параметры под целевую задачу.
Но разреженная сеть может обладать значительно меньшим числом параметров, чем исходная плотная, и тем не менее не сильно проигрывать ей в качестве. Значит, в сети существует некоторая подсеть, которая способна воспроизвести целевую зависимость. Возможно ли, хотя бы гипотетически, обнаружить данную подсеть и обучить разреженную модель за тоже число шагов до сопоставимого качества? Как будто если бы некий высший разум мог подсветить неоновым свечением веса в этой подсети. Или получение эффективной разреженной сети возможно только из обученной плотной модели?
Ответы на обозначенные выше вопросы дает серия работ, посвященных Гипотезе Лотерейнего Билета (The Lottery Ticket Hypothesis / LTH) .
The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks
Впервые явление было обнаружено в работе (Frankle & Carbin)(получившей Best ICLR paper reward). Авторы обучили ряд полносвязных и сверточных моделей на MNIST и CIFAR10 и наглядно продемонстрировали существование подсетей, которые обучаются не менее эффективно (а зачастую даже и более), чем исходная плотная сеть при прочих равных параметрах процедуры обучения. Как будто, если бы эти подсети оказались случайно очень удачно пронициализированы, выигрыли в лотерею по инициализации весов.
Гипотеза лотерейного билета.
Случайно инициализированная плотная нейронная сеть содержит в себе подсеть, способную достичь того же качества на тестовых данных, что и исходная сеть за то же или меньшее число итераций, что и исходная плотная сеть.
(Frankle & Carbin, 2019)
Но как обнаружить такую подсеть? Авторы оригинальной статьи предлают использовать Iterative magnitude pruning: стартуя с плотно инициализированной сети, обучаем нейронную сеть до сходимости, убираем фиксированную долю наименьших по модулю весов, получив некоторую бинарную маску , фиксируем ее, и возвращаем веса к исходной инициализации. Далее повторяем процедуру обучения для прореженной сети, убираем еще некоторый процент весов, получив маску
и снова переинициализируем веса. И так несколько итераций до тех пор, пока желаемая степень прореживания модели не будет достигнута.
О различии между Iterative and Gradual magnitude pruning
При Gradual pruning (постепенном прореживании) после каждого шага прореживания модели (увеличения доли нулевых весов), обучение продолжается из полученной конфигурации весов. При Iterative pruning (итеративном прореживании) фиксируется маска нулевых/ненулевых весов, и ненулевые веса возвращаются к значениям при инициализации.
-
percent.

Fig. 1: What, How, When and How often to prune?
How to rank weights to prune?: There are many more or less heuristic ways to score the importance of a particular weight in a network. A common rule of thumb is that large magnitude weights have more impact on the function fit and should be pruned less. While working well in practice, this intuitively may seem to contradict ideas such as L2
Имеет место ряд важных нюансов и наблюдений:
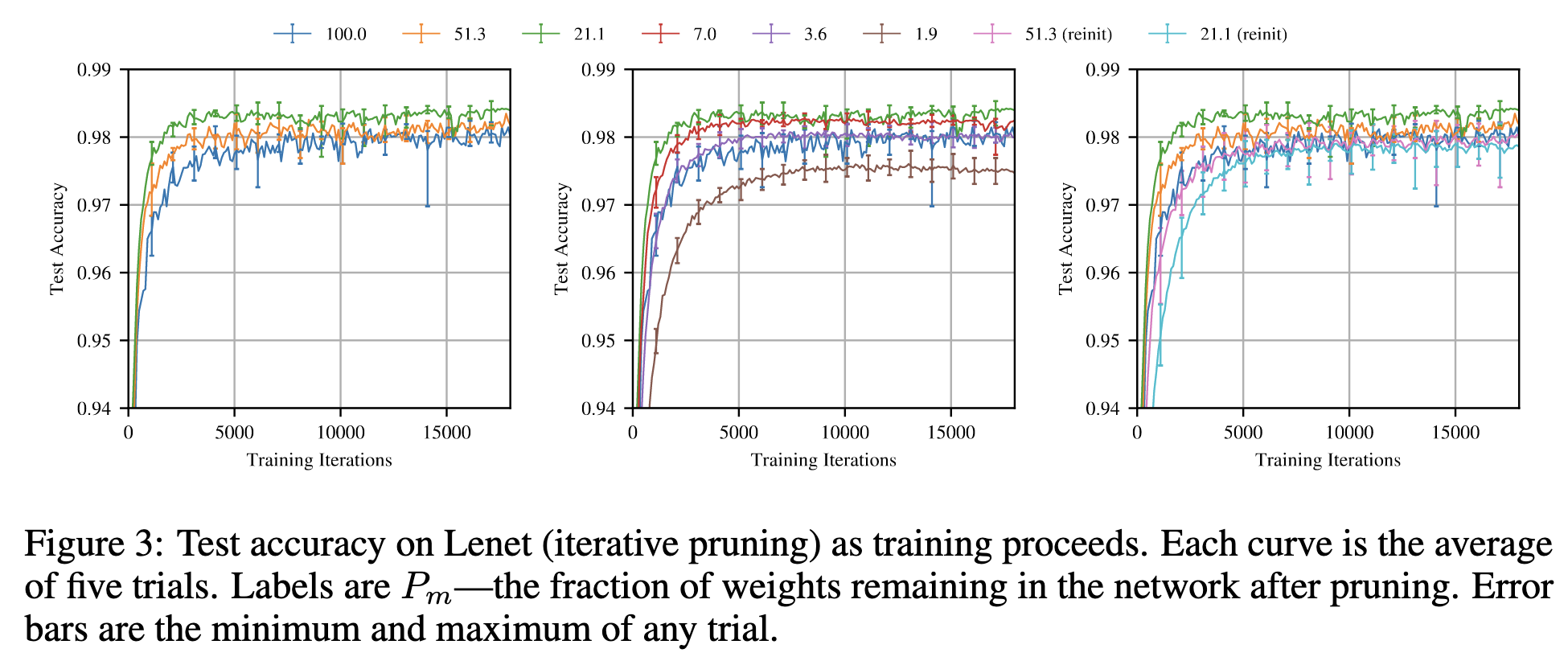
Маска прореживания привязана к конкретной иниализации. Если после прореживания инициализовать ненулевые веса случайным образом, то спарсифицированная сеть уже не будет обладать никакими чудесными свойствами.
При тех же параметрах обучения - расписании learning rate, регуляризациях, разреженные сети сходятся даже быстрее, чем исходные плотные (зеленая кривая, соответствующая 21.1% ненулевых весов сходится лучше всего и достигает наилучшего качества). Вероятно, эффект вызван тем, что запруненные сети менее подвержены выучиванию ложных закономерностей. Но данное свойство присуще только очень специфичному выбору маски, который при случайным семплировании маски произойдет почти с нулевой вероятностью. Поэтому эффект и в некотором смысле назван лотерее, ибо потенциальны выигрыш немаленький, но его шанс крайне мал.
Для более серьезных сетей чем LeNet приходится повозиться с learning rate, тонко настроить его и добавить warmup (постепенное повышение learning rate от 0 до максимального значения)
-
Можно пытаться генерировать маску "лотерейного билета" одной итерацией прунинга, но итеративная процедура выдает лучшие маски (синие кривые лучше зеленых).
![Иллюстрации к тезисам [1-4]
Из статьи The Lottery Ticket Hypothesis Иллюстрации к тезисам [1-4]
Из статьи The Lottery Ticket Hypothesis](https://habrastorage.org/getpro/habr/upload_files/f18/641/bf2/f18641bf2307fdec2b61cdef7bac0be7.png)
Иллюстрации к тезисам [1-4] Из статьи The Lottery Ticket Hypothesis
Основной итог в том, что в данной сети действительно существует подсеть , которая не только может выдать то же качество, что и большая сеть, но и обучиться до него. Однако, поиск такой подсети - трудоемкий и долгий процесс, требующий вычислительных затрат в несколько раз больших, чем обучение исходной плотной сети. Если для MNIST и CIFAR10 это еще терпимо, то для чего-то посерьезнее типа ImageNet, не говоря уже о обучении LLM, данный подход становится неприлично дорогим.
Stabilizing Lottery Ticket Hypothesis
Критически настроенный читатель может заметить, что до сих пор пока были рассмотрены только игрушечные архитектуры и задачи, и не очевидно, будет ли гипотеза иметь место на сколь-либо серьезных задачах. Тем более, что даже в исходной работе пришлось немного поколдовать с learning rate.
Увы, как была показано в последующих работах (Liu et al., Gale et al.), процедура, описанная в оригинальной статье, не позволяет найти подсети с замечательными свойствами.
Однако, если скорректировать формулировку гипотезы и иницилизировать веса после прореживания не начальными значениями , а полученными через небольшое по сравнению со всей процедурой обучения количество шагов
, то лотерейные билеты находятся и для больших сетей без тонкой настройки learning rate, что и было продемонстрировано в работе (Frankle et al.).
Гипотеза лотерейного билета с перемоткой (rewinding)
Рассмотрим плотную, случайно инилиализированную сеть
, достигающей качества
через
итераций. Пусть
веса сети на шаге обучения
Тогда существует шаг
и фиксированная маска
(где
такая, что подсеть
обучается до качества
за
итераций.
Как было показано на экспериментах с CIFAR10, перемотка на 100 итерацию обучения для VGG-19 (500 для ResNet-18) приводит к значительному приросту качества, в то время как перемотка в начальный момент времени не то, чтобы лучше, чем просто случайная иниализация весов.
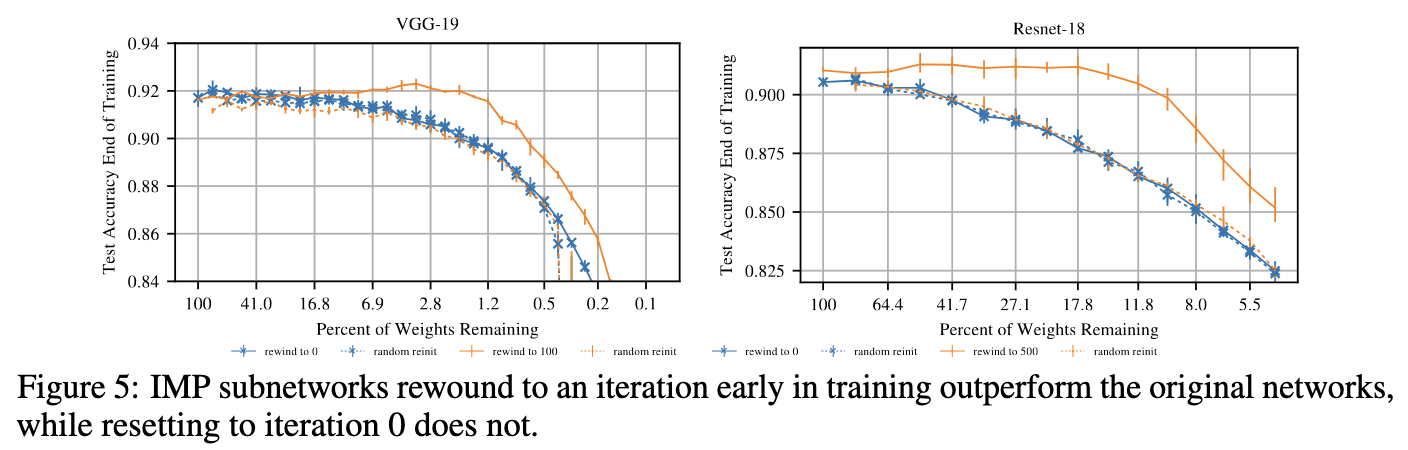
При такой постановке гипотеза масшабируется уже на вполне серьезные сети и задачи. Ниже представлены графики accuracy vs sparsity для актуальных по тем временам сверточных сетей.
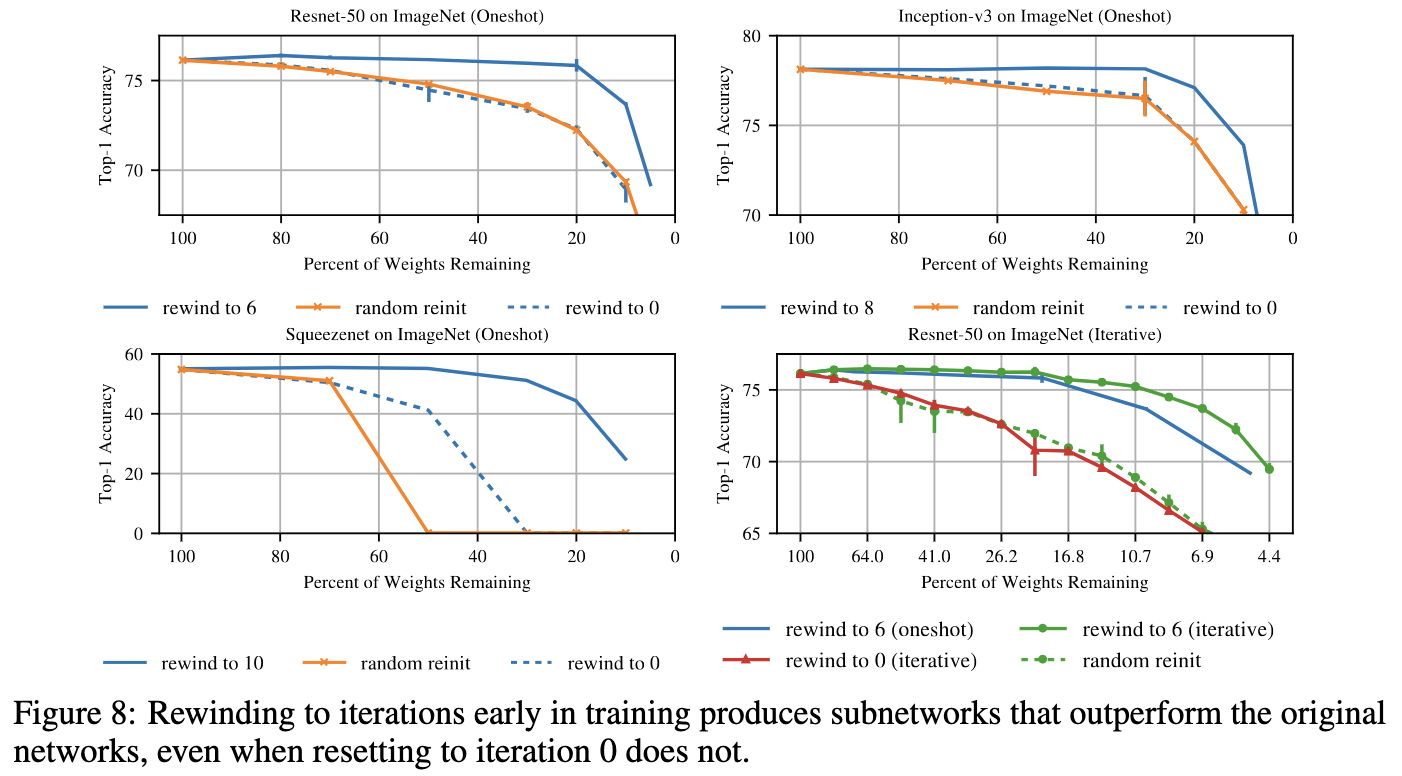
Однако при такой постановке называть билет "лотерейным" не совсем было бы корректно, поэтому для таких паттернов прореживания был придуман термин matching ticket (то есть сооветствующая некоторому хорошему решению).
Linear mode connectivity and the Lottery Ticket Hypothesis
Наблюдая некоторое явление или свойство, исследователь хочет понять, чем оно вызвано, найти какое-то логическое обоснование или заглянуть внутрь.
В статье (Frankle et al.) те же самые авторы, что и в прошлой статье, исследуют связь между Lottery Ticket Hypothesis и линейной связностью решений.
Суть явления в следующем. Лосс поверхность большинства нейронных сетей, встречающихся на практике, обладает сложной существенно невыпуклой структурой, с множеством холмов, долин и впадин.

Обыкновенно при обучении нейронных сетей используется та или иная вариация алгоритма стохастического градиентного спуска (SGD) со случайным выбором и порядком примеров из обучающей выборки, что вносит некоторой элемент случайности в процедуру обучения. В начальный момент веса нейронной сети совершают множество резких и непредсказуемых телодвижений, в результате чего при различных запусках из одной исходной точки, с разными факторами случайности, SGD может сойтись к очень разным решениям, с большой вероятностью разделенными барьером с высоким значением функции потерь.
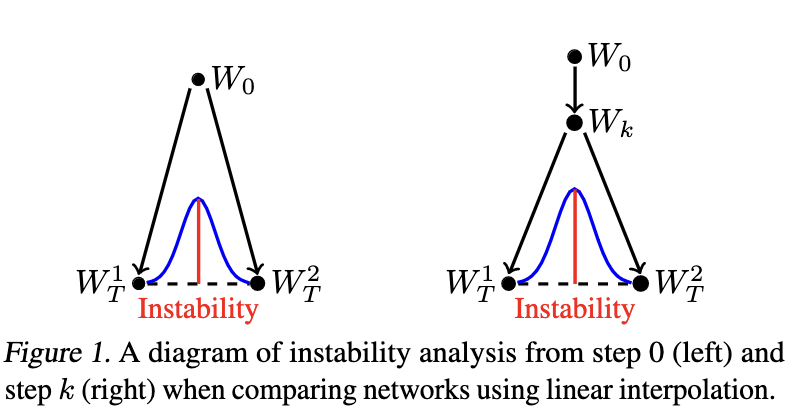
Отсюда возникает желание посмотреть на то, что произойдет если соединить два решения, к которым сошелся SGD при разных случайных факторах, прямой, и посмотреть на то, как будет меняться значение целевой функции при переходе от одного решения к другому. То есть, если SGD сошелся к решениям и
, рассмотрим их линейную комбинацию
c
. Если веса разделены барьером, то где-то при переходе от одного веса к другому неизбежно придется подняться вверх по горе, оказавшись в области с большим значением лосс-функции. Если же решения, расположены в одной долине, то нет оснований для значительного возрастания функции потерь.
Авторы вводят понятие нестабильности - разницы между максимальным значением ошибки на пути, соединяющем два решения и средним арифметическим значений функции ошибки
. Под ошибкой подразумевается, например, доля неверных ответов в задаче классификации.

Далее авторы исследуют зависимость определенной выше нестабильности в зависимости от времени обучения . Для простых сетей типа LeNet нестабильность не возникат или пренебрежимо мала, но имеет место для любых сколь-либо серьезных архитектур.
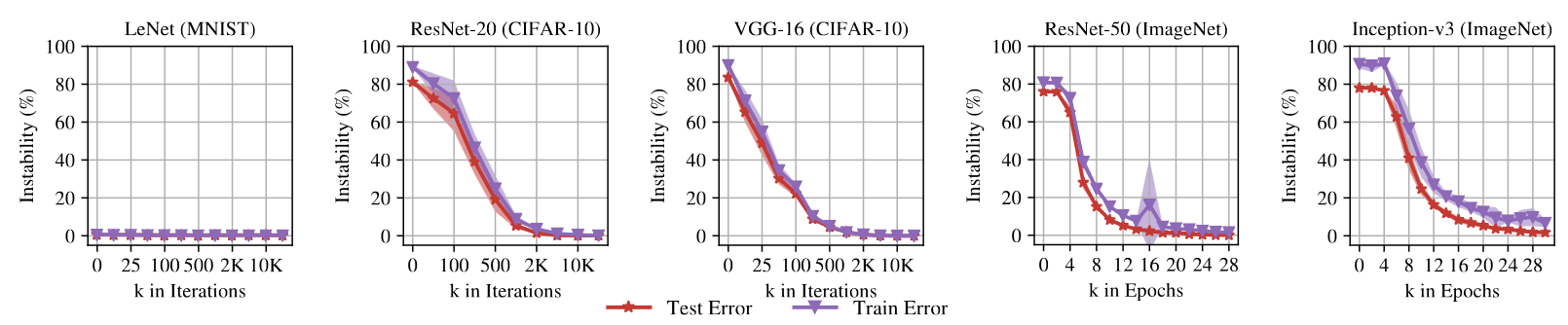
Какое это имеет отношение к Lottery Ticket Hypothesis, спросите вы?
Как было обозначено в прошлой статье начиная с некоторой итерации возникает явление matching networks. И это
, как утверждается, то же, что и время, начиная с которого веса не разьезжаются по разным долинам.
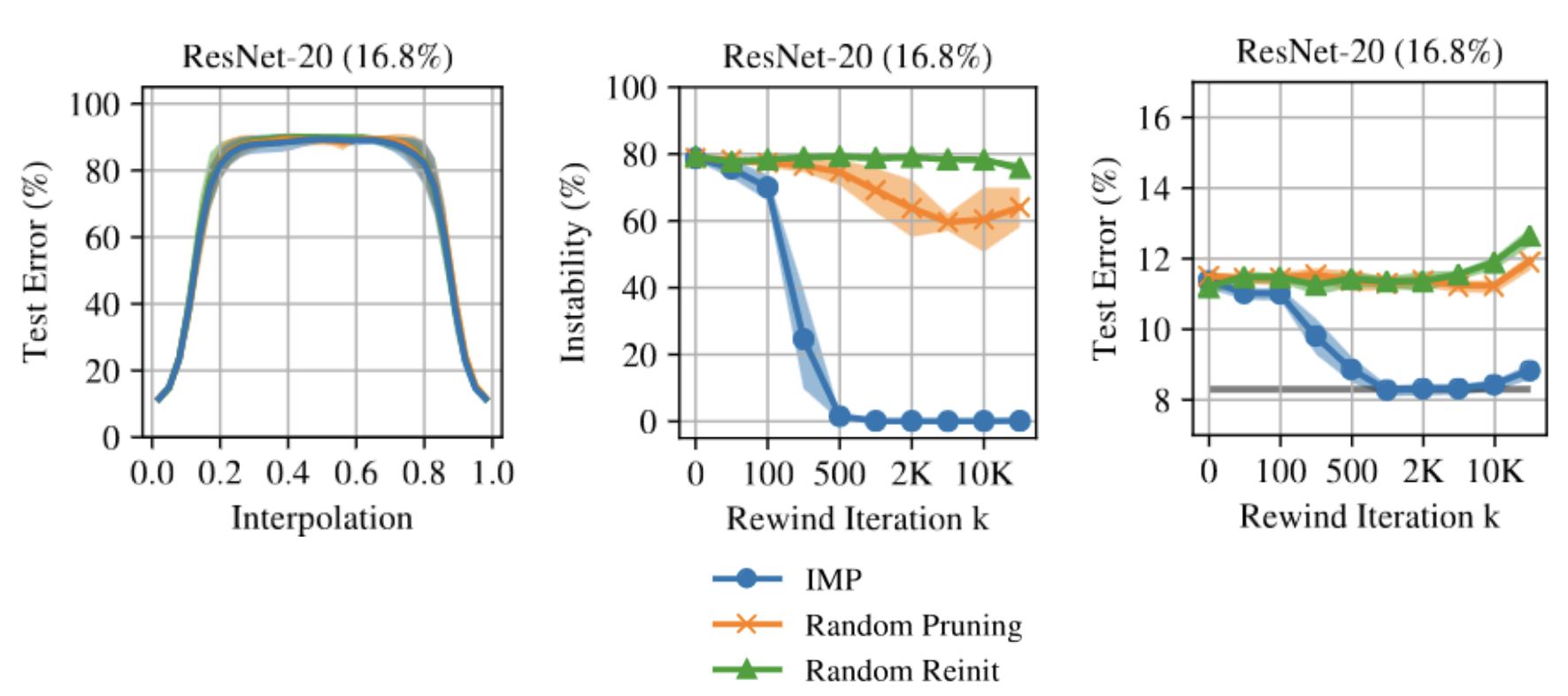
Кроме того, в этой статье вводится понятие 3 режима прореживания.
При небольшом прореживании даже случайный выбор маски позволяет достигать хорошего качества на задаче.
Во втором режиме требуется уже осмысленный выбор маски прореживания, чтобы добиться matching, качества близкого к исходной модели. Случайное прореживание приводит к значительной просадке в качестве, но все еще существует итерация, начиная с которой исчезает барьер между двумя решениями с разной стохастичностью. Номер этой итерации растет со степенью прореживания.
-
В третьем режиме уже даже IMP не может найти matching subnetworks. Тем не менее явление стабильности все еще наблюдается для полученных с помощью IMP нейросетей.
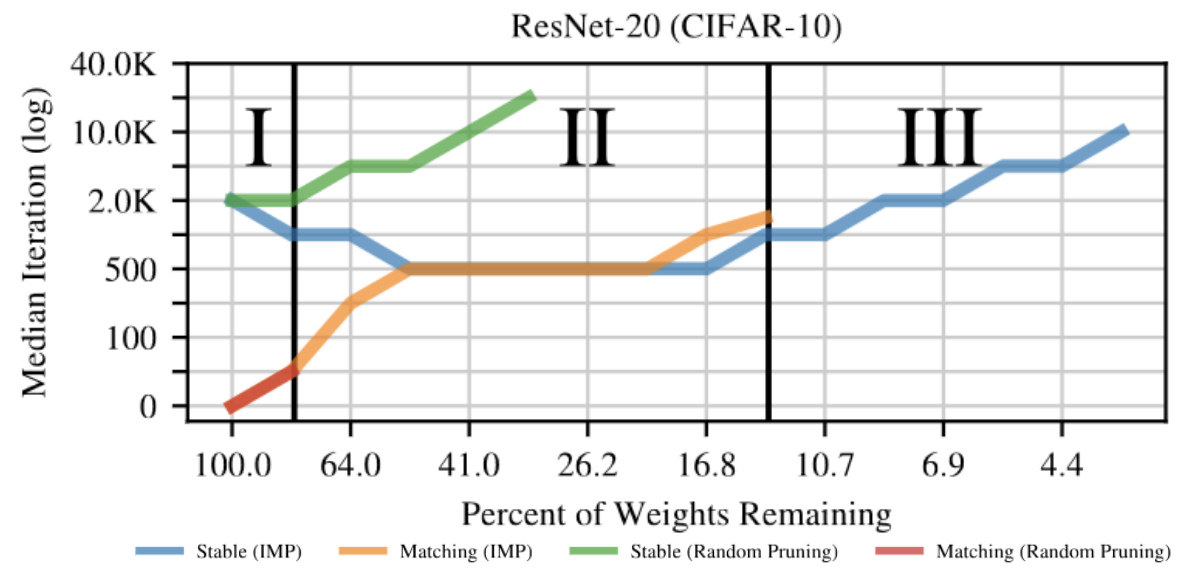
Три режима прореживания нейронных сетей Из статьи Linear mode connectivity and the Lottery Ticket Hypothesis
Drawing Early-Bird Tickets: Towards More Efficient Training of Deep Networks
Как бы ни занятна и интересна не была наука про лотерейных билеты, проблемным местом остается проблема их эффективного нахождения. Обучать сеть до сходимости несколько раз удовольствие не из дешевых. Можно ли их обнаружить раньше?
В работе (You et al.)предлагается генерировать winning tickets в процессе обучения, и, как оказалось, начиная с некоторой итерации обучения, полученные подсети уже не сильно уступают в качестве полученным из модели при сходимости.
Замечание. В отличие от предыдущих работ данная работа про структурированное прореживание, когда зануляются не отдельные веса, а сверточные каналы целиком. Критерием важности сверточного канала является мультипликативный фактор в следующем на сверткой слое батч нормализации.
Основная мотивация подхода в том, что оптимизация нейронных сетей имеет двухфазный характер:
Выучивание низкочастотных компонент, соотвествующих большим сингулярным числам. То есть запоминание самых общих и грубых черт задачи.
Фаза тонкой настройки. Выучивание меньших по величине сингулярных значений.
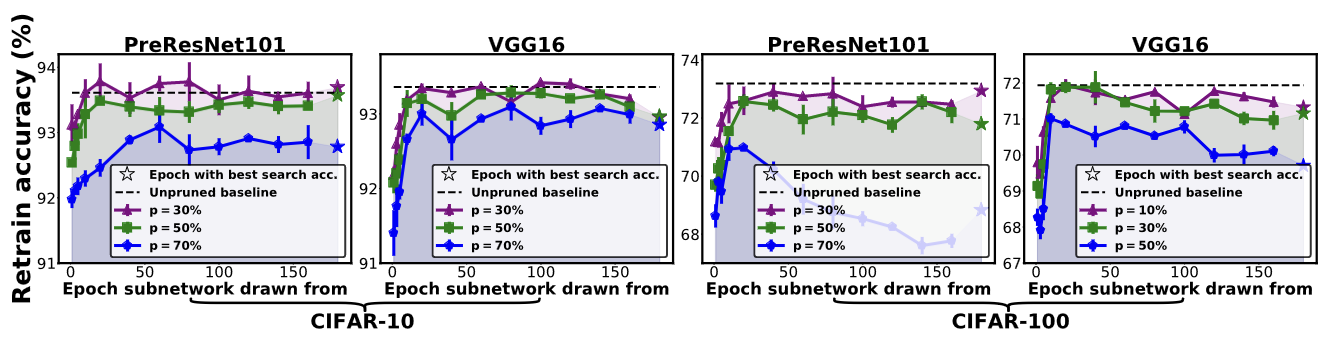
Поэтому наибольшие изменения весов происходят в первоначальный момент времени, а дальше веса меняются относительно слабо, что и позволяет предположить, что разумно искать winning tickets задолго до сходимости к оптимуму.
Как и веса нейронных сетей, маски прореживания сильно меняются на ранней стадии обучения, но постепенно устаканиваются. Для определения расстояния между двумя масками используется расстояние Хэмминга (Hamming distance).
Так как полученные подсети находятся задолго до конца обучения, авторы предлагают их называть early-bird (EB) tickets (ранними пташками).

Отсюда и следует способ обнаружения масок - обучаем модель, постепенно увеличивая степень прореживания. Если расстояние между двумя масками на двух последовательных итерациях прунинга меньше некоторого заданного порога , прекращаем прореживание, фиксируем маску и затем повторяем исходную процедуру обучения с найденной маской, чтобы достичь высокого качества на задаче.
One ticket to win them all: generalizing lottery ticket initializations across datasets and optimizers
Следующий вопрос, которым уместно было бы задаться: насколько привязаны лотерейные билеты к конкретному датасету (MNIST, CIFAR10, ImageNet), процедуре обучения (оптимизатору, аугментациям и регуляризациям) и задаче (классификация, сегментация, детекция)? Сходу так не очевидно, будет ли найденная при одной постановке задачи подсеть сколь-либо особой при изменении хотя бы одного из перечисленных ингридиентов. Однако можно предположить, что в процессе обучения сеть выучивает некоторые полезные inductive biases и характер соединений
В работе (Morcos et al.) авторы решили проверить гипотезу о переносимости matching tickets с одного датасета на другой, взяв 6 датасетов различного размера и сложности (Fashion-MNIST, SVHN, CIFAR10, CIFAR100, ImageNet, Places365). Процедура довольно проста:
Получаем matching ticket на исходном датасете с помощью IMP.
Обучаем полученную matching ticket до сходимости на новом датасете
Тонким местом здесь является тот факт, что входной размер изображения может вариьроваться между разными датасетами (впрочем, можно делать resize к некоторому заданному разрешению), и разные задачи классификации различаются в числе меток, которые предполалается предсказывать. Первый казус разрешается сравнительно легко в случае сверточных сетей вставкой в конец (она и так по умолчанию в ResNet-ах, но не в VGG) адаптивного pooling слоя, который собирает карту признаков произвольного размера в один вектор. А во втором случае мы просто инициализируем случайным образом линейный слой в конце (тем более что в литературе по прунингу обычно не спарсифицируют первый и последний слой).
И что же получилось?
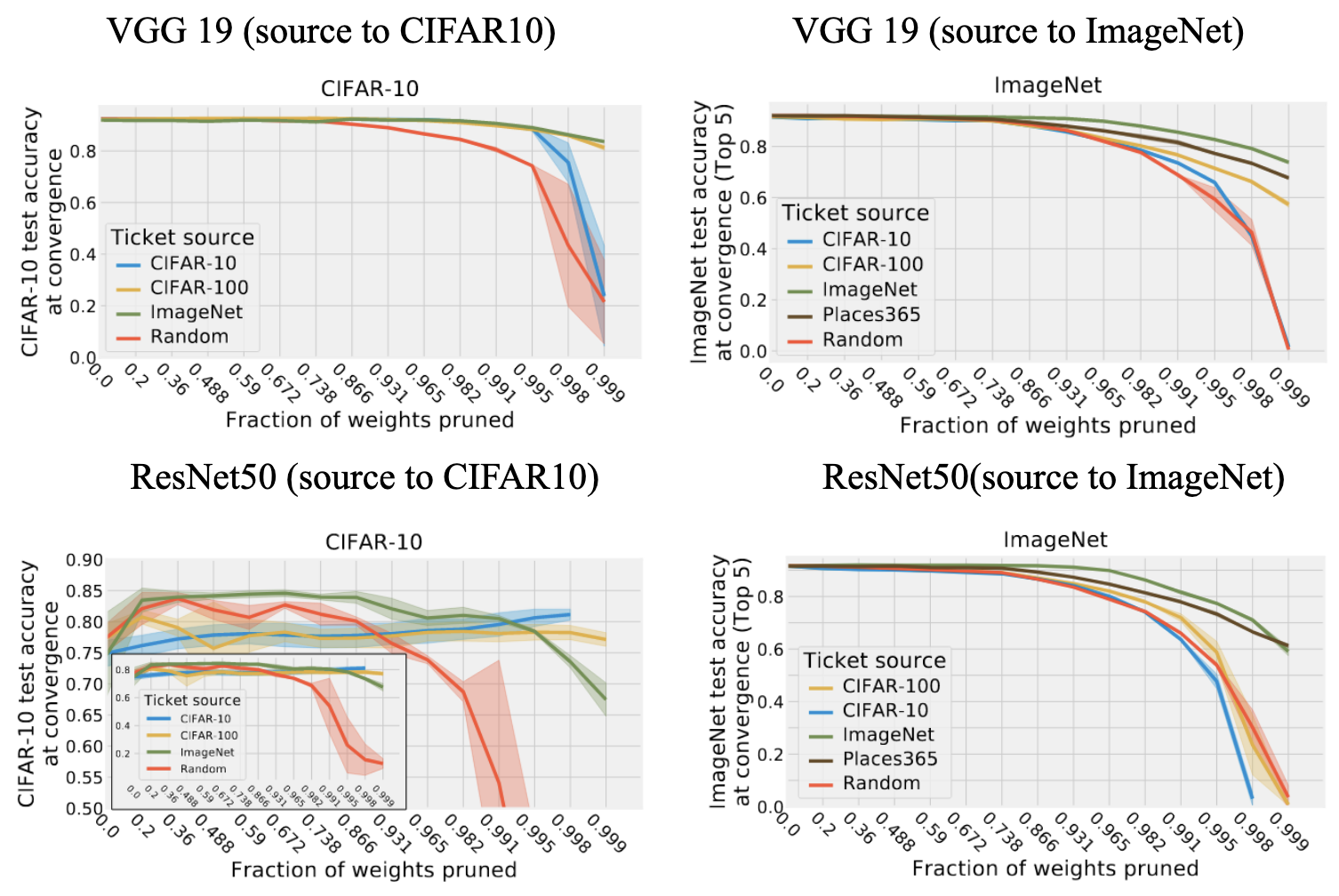
На VGG-19 трансфер маски с большого датасета на маленький работает хорошо, даже лучше чем matching ticket, обнаруженный на самом целевом датасете . По всей видимости, маска полученная на большем количестве данных обладает некоторой универсальностью. Некоторая польза при переносе маски в обратную сторону (с меньшего на больший датасет) тоже есть, хоть и разница со случайной маской не столь существенна. Что впрочем, ожидаемо. Чем сложнее датасет, тем лучше трансфер.
Для ResNet50 выводы в целом похожие, хотя при большом прореживании маска на ImageNet работает хуже, чем с исходного датасета, и кажется, что маски с CIFAR10 работают примерно так же, как и случайная.
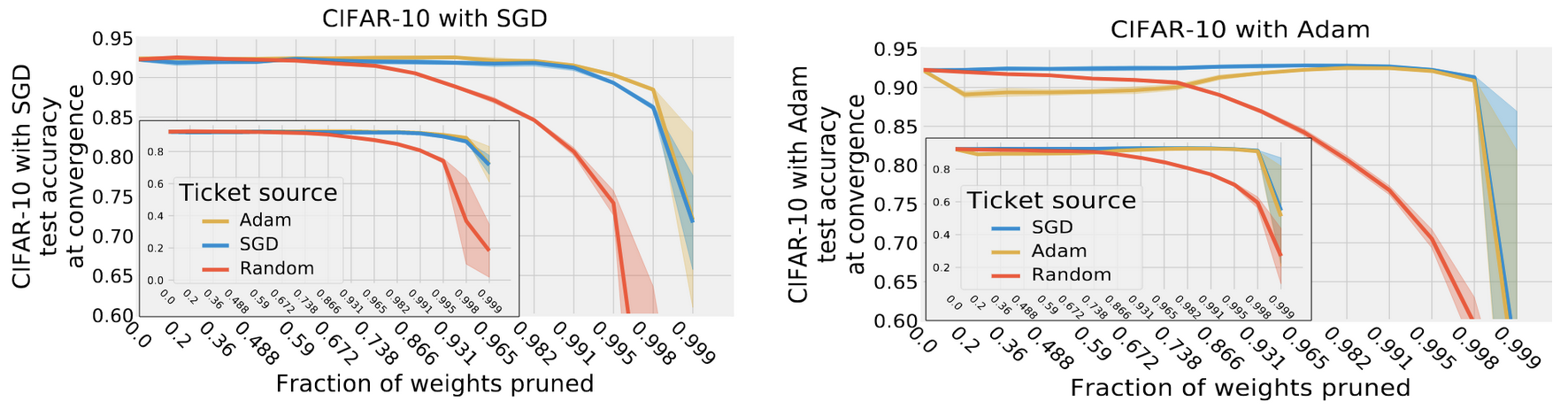
Кроме того, авторы проверили переносимость маски, полученной при обучении с одним оптимизатором (SGD или Adam) на другой. Как оказалось, matching tickets обобщаются на разные оптимизаторы, что, на мой взгляд, является весьма нетривиальным результатом, так как траектория обучения у SGD и Adam должна вообще говоря существенно отличаться (из-за наличия обуславливания на дисперсию градиентов в Adam). Однако как маска, полученная при обучении с SGD переносится на Adam без существенной просадки в качестве, так и наоборот.
Интересно было еще посмотреть, насколько данный результат обобщается на более современные архитектуры - Vision Transformers и их производные, обучение с простыми аугментациями (RandomCrop/Flip) и сложные процедуры с RandAugment, Mixup, Cutmix, SAM, и прочими модными наворотами. И раз уж маска хорошо переносится с большого датасета на маленький, можно ли получить с помощью хорошего self-supervised, contrastive loss преобучения - DINO, CLIP, MAE универсальную маску для downstream задач.
Unmasking the Lottery Ticket Hypothesis: What's Encoded in a Winning Ticket's Mask?
И напоследок свежачок с грядущей ICLR23.
Данная работа (Paul et al.) делает попытку разобраться с причинами успеха IMP для поиска matching tickets с точки зрения геометрии лосс-поверхности. Еще в первой работе по теме было обнаружено, что итеративное прореживание работает лучше, чем однократное, но обьяснения данного явления до сих пор в литературе не было представлено.
Основные находки и результаты данной работы следующие:
Если найденные при последовательном прореживании на шагах
и
подсети matching, они линейно связаны между собой, то есть между ними нет лосс-барьера. При этом, они могут быть отделены от плотной сети областью с высокими значениями функциями потерь.
При больших степенях прореживания найденные сети обладают большой стабильностью не только к шуму SGD но и случайным возмущениям весов порядка расстояния между последовательными matching tickets с возрастающей степенью прореживания.
Magnitude pruning в IMP выбирает более плоские направления по сравнению со случайным прореживанием.
Как и более поздние работы по этой теме, авторы рассматривают обычно инициализиацию исходными весами, а через некоторое количество шагов обучения IMP with rewinding. Если пытаться соединять подсети при IMP с инициализацией в начальный момент времени или слишком ранний, то между ними возникает барьер. Но если выбрать нужную итерацию, то линейная связность имеет место.
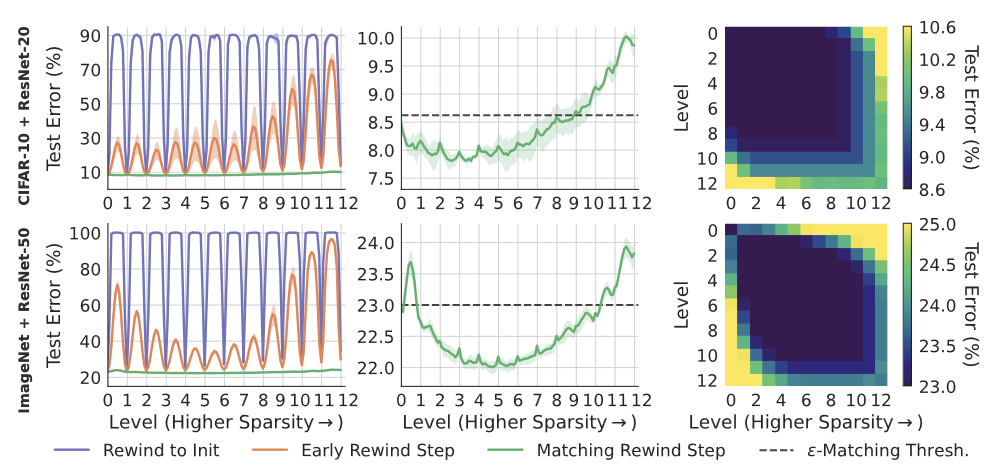
Следующим интересной находкой является тот факт, что начиная с какого-то шага прореживания (который может быть самым первым, а может и не быть), прореженные сети на шагах и
попадают в одну и ту же долину с низкими значениями функции потерь. Пока степень прореживания не очень велика, подсеть, полученная на следующем шаге оказывается в пределах окрестности вокруг решения с прошлого шага, где ошибка не возрастает существенно. При дальнейшем прореживании сеть может уже не попасть в пределы
области с высоким качеством модели, но тем не менее все равно попадет в ту же долину с относительно низким значеним лосса.
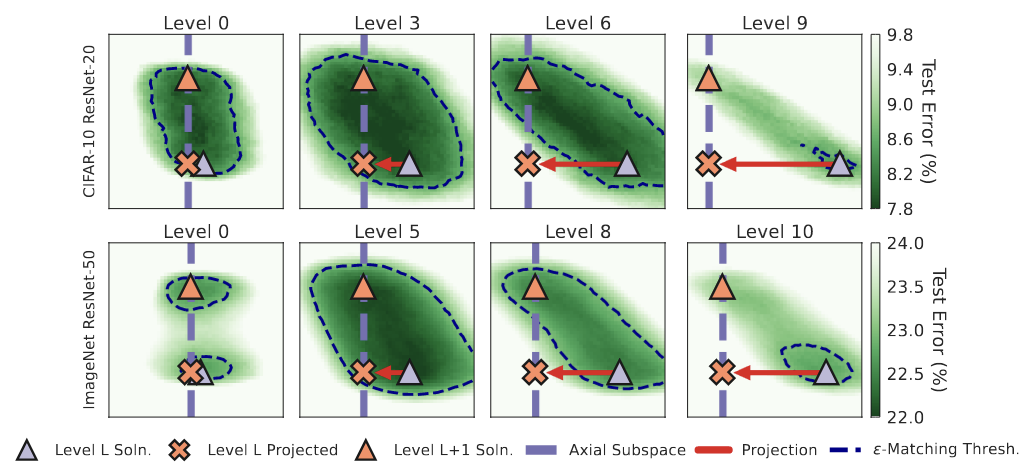
И в конце авторы иллюстрируют тезис про то, что Magnitude pruning выбирает более плоские направления на лосс-поверхности.
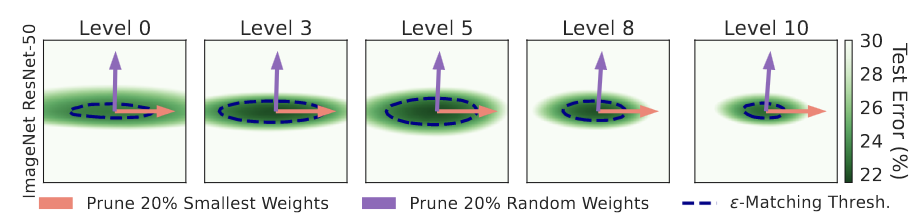
Заключение
Существование lottery/matching tickets является очень красочной и убедительной иллюстрацией утверждения, что нейронные сети обладают в себе избыточностью, и то что в них существует всегда или почти всегда подмножество весов, которое хорошо решает исходную задачу. Однако, наличие большого числа параметров в сети повышает вероятность возникновения подсети с чудесными свойствами.
Кроме того, фундаментальной и пока нерешенной задачей является эффективная процедура их нахождения. Как алгоритм прунинга, они имеют право на существование, но Gradual Pruning, процедуры разреженного обучения (Evci et al., Peste et al.) значительно эффективнее.
Данная тема очень неплохо заходит на топовых конференциях по машинному обучению (NeurIPS, ICLR, ICML). Как говорится, lottery paper hypothesis: make all ICLR submits spotlights!
Комментарий по поводу последнего предложения
Отсылка к статье Rigging the Lottery: Making All Tickets Winners
Надеюсь, было интересно и познавательно. Комментарии и замечания привествуются!
Дополнительная литература и ссылки
[1] Отличный блог, во многом на который я опирался при написании поста
[2] Выступление от самого творца гипотезы на семинаре DeepMind
[3] GitHub репозиторий на tensorflow с реализацией экспериментов из первой статьи


19blackadder97 Автор
В разделе, посвященном первой статье, возникает где-то посередине картинка (блок-схема) с комментариямии на английском. Это не фича, а баг, в редактируемой версии ее просто не существует.