Всем привет! В данном посте я хотел бы рассказать про весьма интересную и важную деятельность в области глубокого обучения как прореживание (прунинг) нейронных сетей. На просторах сети есть неплохие материалы по данной теме, например, статья на Хабре трехлетней давности.

Здесь будет приведен общий обзор основных методик прореживания нейронных сетей, разработанных человечеством в его (почти) безграничной изобретательности, а в последующем я планирую рассмотреть некоторые подходы более подробно. Вообще говоря, идей на самом деле существует гораздо больше, чем будет рассмотрено ниже, здесь я приведу самые популярные подходы в подробностях, пропорциональных пониманию автором конретного метода.

Поехали!

Определение и мотивация

Прунинг нейронных сетей - это метод сжатия (уменьшения расхода памяти и вычислительной сложности) сети за счет устранения части параметров в предобученной модели.

Желание облегчить и упростить модель достаточно естественно, в каком-то смысле. Современные успехи и бурное развитие в сфере глубокого обучения обусловлено не только разработкой огромного количества новых архитектур и вовлченностью большого числа людей в данной области, но и сильно возросшими вычислительными мощностями (власть, которая и не снилась моему отцу). Увесистые нейронные сети с миллионнами (миллиардами) параметров стало возможно обучать благодаря массовому распространению высокопараллельных вычислитей - GPU, TPU  и т.д, которые еще можно обьединять в целые кластера.

Тем не менее, во многих приложениях и обыденных ситуациях возможности запустить сеть на мощной карточке с тысячей CUDA ядер нет. В качестве простого примера приведу использование нейронных сетей на смартфонах для задач интеллектуаьной сьемки и обработки фото и звука. Само собой, впихнуть в смартфон Нвидиевскую V100 - так себе вариант, ибо такое устройство будет не только весить не меньше 1.5 кг, но еще потреблять 300 Вт, для чего придется с собой вдобавок таскать блок питания. В общем, так себе удовольствие.

В то же время, как известно, нейронные сети перепараметризованы - многие параметры в сети излишни и мало влияют на конечный выход нейронной сети. И отсюда возникает идея - взять хорошо обученную модель и устранить в ней как можно больше весов и операций, при этом не потеряв существенно в качестве. Более того, при небольшом прореживании обычно наблюдается повышение качества на тестовой выборке. Предположительно, ликвидация лишних параметров убирает "шумные веса" из модели и разрушает случайные закономерности, которые сеть обнаруживает на обучающей выборке, но не являющиеся характерным для всего распределения данных в целом.

Данная идея весьма не нова, и ведет начало не от Адама и Евы, но в достаточно далекие времена (конец 80-х - начало 90-х), когда число параметров в нейронных сетях не превышало нескольких тысяч и глубокое обучение было уделом сравнительно узкой группы энтузиастов.

Классификация

Во-первых, методы прореживания сети можно разделить на две большие категории:

1. Прунинг на уровне модели.

   Веса из сети устраняются окончательно и бесповоротно. Для каждого примера из обучающей или тестовой выборке используются те же веса при инференсе (inference).

2. Эфемерное прореживание (Ephemeral sparsity).

   Веса из сети не убираются, но при каждом проходе в вычислении функции используется только часть параметров модели или активаций с прошлых слоев. В качестве известных примеров можно привести Dropout, где часть случайно выбранных весов зануляется, (да-да, целью дропаута явялется регуляризация, а не прореживание, но тем не менее) и Switch Transformer.

В этом обзоре я буду рассматривать первую категорию. Кроме того, прунинг можно разделить на:

1. Неструктурированный прунинг.

   Прореживание модели проводится на уровне отдельных весов. Полученная маска активных весов, вообще говоря, имеет хаотическую структуру.

2. Структурированный прунинг.

   Прореживание проводится на уровне целых сверточных фильтров или даже слоев в сети. Кроме того, можно прореживать веса не по отдельности, а блоками, организованными по соседству.

Первый подход позволяет обычно добиться большего количества зануленных весов, но при этом дает меньше преимуществ в реализации на реальном железе, так как вычисления обычно паралеллизованны и проводятся на уровне векторов и матриц. Специальные структуры данных для разреженных матриц (sparse matrix), такие как CSR (compressed sparse row), CSR (compressed sparse column) и COO (coordinate offset) дают преимущество только если матрица сильно разреженная  (не более 10% ненулевых элементов).

Далее, методы можно разделить на

1. Прореживающее модель глобально

   Для прореживания используется информация со всех слоев сети.

2. Прореживающие послойно

   Прореживание слоев проводится независимо.

Обучение прореженной модели

Существует несколько стратегий по прореживанию моделей:

1. Однократное прореживание (One-shot pruning).

   Берется предварительно обученная модель и в определенный момент устраняется некоторая часть весов согласно алгоритму прореживания. Можно на этом этапе оставить все как есть, но обыкновенно продолжают обучение на протяжении еще некоторого количества эпох, тем более, что при использовании более грубых методов, вроде magnitude-based, качество первоначально может заметно просесть и восстановиться до уровня близкого в исходной модели, только после оптимизации. При этом важно дождаться сходимости к оптимуму, так как если проредить еще не оптимальную модель, итоговое качество будет несколько хуже.

2. Итеративное прореживание

   Модель прореживается постепенно. Через число шагов, определенных расписанием прореживания (pruning schedule), часть весов устраняется из модели, затем проводится дообучение модели. Данная процедура проводится некоторое количество раз до тех пор пока модель не достигнет требуемой разреженности. Здесь, как можно заметить, довольно большой простор для подбора гиперпараметров - сколько весов отбросить на данной итерации, сколько эпох обучать модель между каждой итерацией.

3. Обучение разреженной модели c самого начала

   Кроме того, можно стартовать сразу с разреженной модели, а затем уже по ходу дела убирать наименее важные веса и заодно наращивать новые веса (которые до этого были обращены в нуль) на основе некоторого критерия. Достоинством данного подхода является возможность обучения моделей, которые в плотном виде (dense) не помещаются в память устройства.

   К данным методам относятся SET, SNIP, RiGL, GraSP.

Различие между подходами показано на картинке ниже:

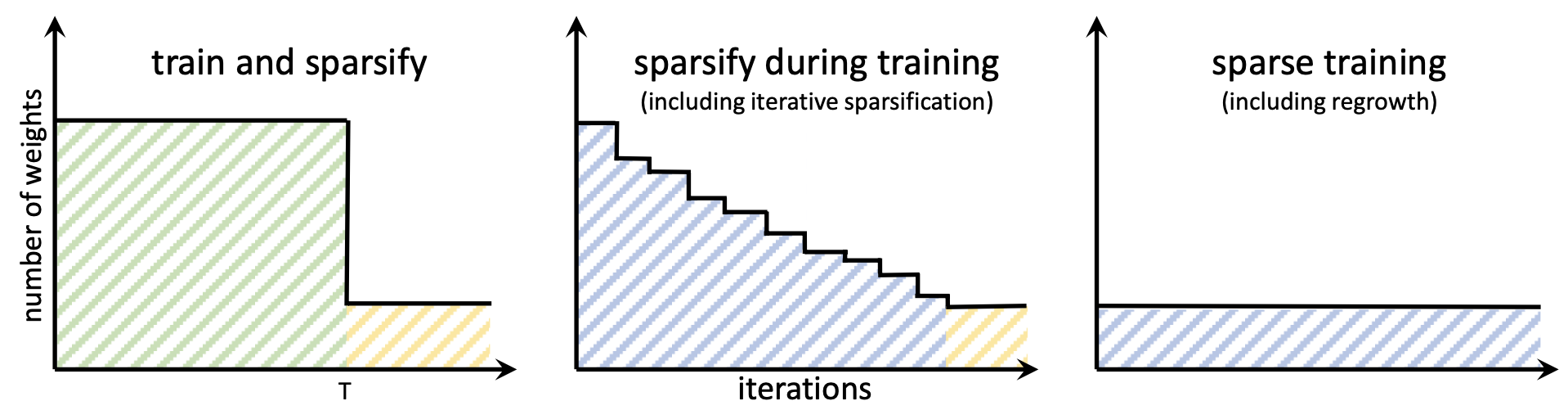
Какая из стратегий является лучшей - до сих пор на этот вопрос нет четкого ответа. Различные источники дают свидетельства в пользу того или иного метода на конкретных примерах.

Критерии отбрасывания весов

Data-free

Данные подходы не используют никакой информации о целевой функции и промежуточных активациях в нейронной сети.

• Magnitude-based pruning

  Одним из простейших и в то же самое время эффективных подходов является magnitude-based pruning, отбрасывающий веса с наименьшей абсолютной величиной . Перемножение матриц, операции свертки неизбежно содержат с себе операцию следующего вида (по повторяющимся индексам подразуемвается суммирование):

  В предположении, что входы среднем имеют величину одного порядка, видим, что веса с наименьшей абсолютной величиной вносят наименьший вклад с сумму. Конечно, вообще говоря, это неправда, но при отсутствии дополнительных данных, довольно разумное предположение. Так сказать, дешево и сердито.

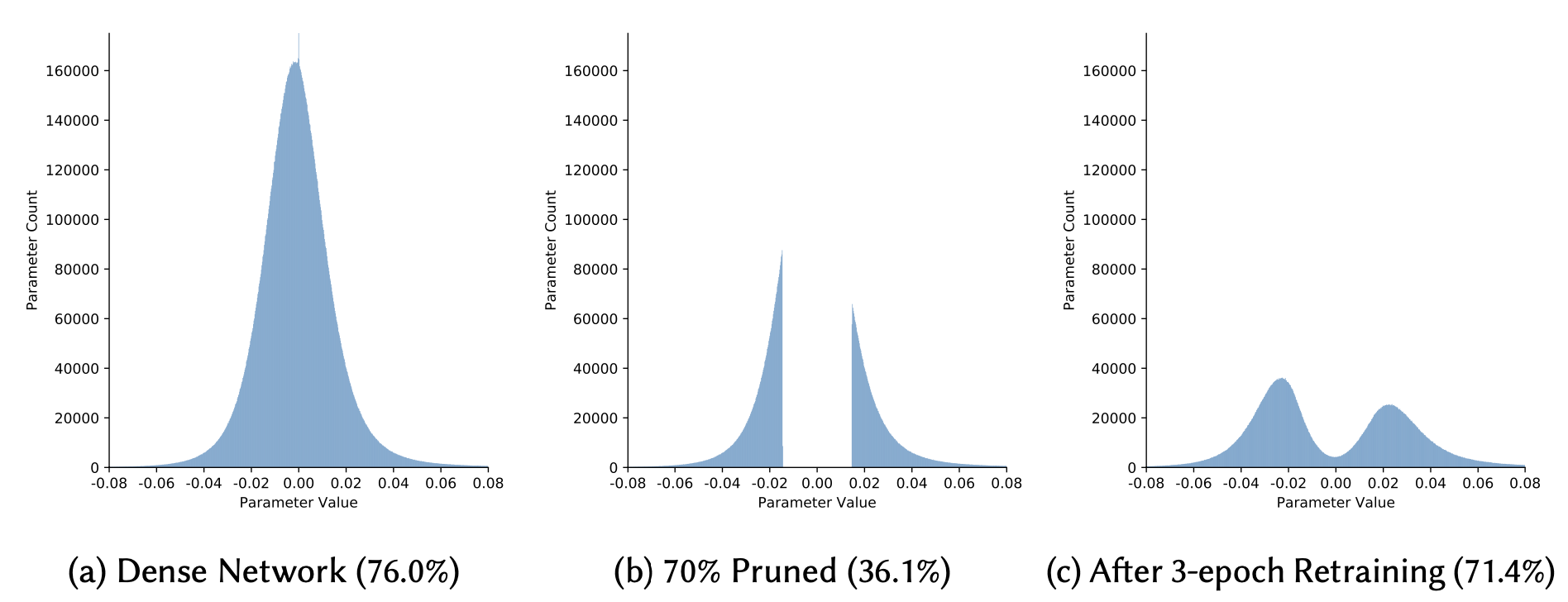
Magnitude-based pruning - один из самых первых методов прореживания сети, предложенный еще в конце 80-х.

Несмотря на простоту, данный метод отрабатывает довольно неплохо на практике, и позволяет до определенного предела отбрасывать веса без потери в качестве предсказаний. Из-за простоты реализации и дешевизны использования на текущий момент - это самый популярный способ прореживания. Дополнительные расходы при обучении сводятся к хранению в памяти масок прореживания весов и построения гистограммы весов раз в одну и нескольких эпох, поэтому этот метод применим и для больших нейронных сетей.

Тем не менее, когда сеть уже сильно разреженная такой подход убирает веса не всегда оптимально, и качество начинает проседать довольно существенно.

Data-driven

Кроме того, можно прореживать нейронную сеть в зависимости от чувствительности выходов к значению конкретного веса.

• На основе дисперсии выходов нейрона

  Если для конкретного нейрона выход меняется незначительно для различных входных данных, то можно просто взять и убрать данный нейрон, и его выход добавить в bias для последующих нейронов. Т.е если , то вполне естетвенно просто заменить нейрон на константу

• На основе величины активации нейрона

  В работе было предложено определять важность нейронов в зависимости от средних значений и дисперсии активаций нейронов на выборке. Идея подхода та же, что и в magnitude-based, но сравнение проводится для нейронов, а не весов, и здесь не делается предположения о примерном равенстве входных значений, которые домножаются на веса.

• На основе взаимной корреляции между весами

  Если в данном слое существуют сильно скореллированые нейроны, которые соединены с одними и теми же нейронами на следующем слое, то можно обьединить несколько нейронов в один, тем самым несколько уменьшив число операций.

Training-aware

• Методы, основанные на разложении лосс-функции в ряд Тейлора (OBD, OBS)

  К данному семейству методов относятся Optimal Brain Damage, предложенный Ле Куном (да-да, тем самым, который классифицировал MNIST) и Optimal Brain Surgeon.

  Предположим, что имеющаяся в распоряжении обучающая выборка достаточно хорошо описывает распределении данных и модель находится в локальном оптимуме (возможно плохом) лосс функции  или по крайней мере в окрестности. Кроме того, наложим нужные требования по гладкости, и тогда в окрестности точки минимума разложим функцию потерь до второго по весам:

Здесь - вектор сдвига от точки оптимума. А - матрица Гессе, составленная из вторых производных функции потерь

В точке экстремума второй член зануляется, а матрица Гессе - положительно определена (полуопределена), иначе существует направление, двигаясь по которому можно уменьшить еще значение функции потерь. Далее ставится следующая задача - найти такой оптимальный сдвиг в пространстве весов, так что один из них в итоге обратится в ноль. Т.е:

Здесь  - единичный вектор в направлении -веса.

Традиционно задача нахождения условного экстремума решается методом введения множителей Лагранжа, что и делают авторы в статье по OBS. Для каждого из весов считают изменение лосс-функции при движении, зануляющем какой либо из весов:

И среди всех весов выбираем такой, для которого рост функции потерь наименьший.

В методе Ле Куна делается предположение, что матрица Гессе - диагональна, т.е:

Тогда критерий отбора сводится к нахождению весов с наименьшеним значением , при этом другие веса не изменяются.

То есть кроме абсолютной величины весов, мы учитываем кривизну повехности функции потерь. Заметим, что OBD сводится к magnitude-based прунингу, когда все равны.

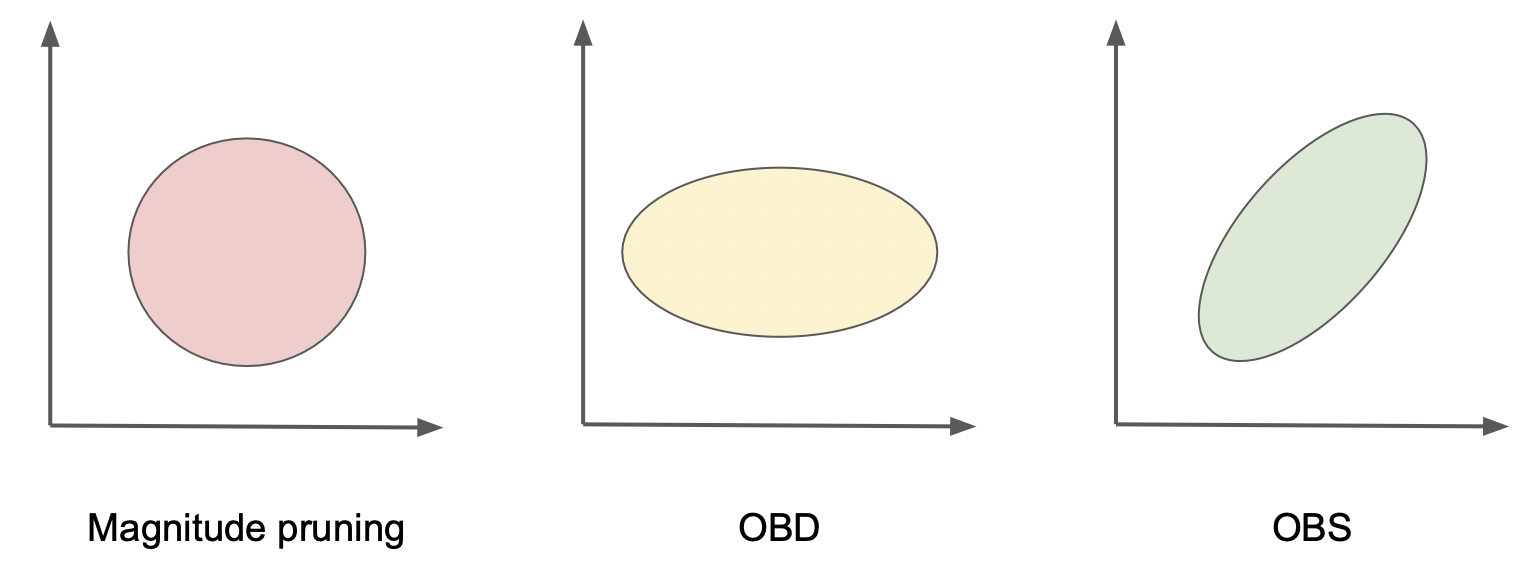
Однако, как было замечено в работе по OBD, в действительности Гессиан существенно не диагонален - поэтому отбирает веса не оптимально. В своей работе авторы сравнили на различных искуственных бенчмарках два метода, и их метод отработал точнее. Заметим, что дело происходило в начале 90-х и возможности прогнать нейросеть на CIFAR-10, не говоря уже про ImageNet, у исследователей не было.

Несмотря на хорошую теоретическую подоплеку, такой подход имеет несколько фундаментальных проблем и нюасов.

1. Во-первых , вычисление матрицы Гессе - очень дорогостоящая с вычислительной точки зрения и по памяти операция.

   В случае, если проводить вычисление для всех пар весов

   требуется память пропорциональная числу весов в квадрате . Для сравнительно маленькой MobileNet-V3 c 2.5 миллионами параметров - это чисел, что даже в bfloat16 дает 12 TB.  Если вашего дядю не зовут Дженсен Хуанг или вам не досталась криптоферма по наследству, то такую матрицу банально не поместить в память системы GPU. А для GPT-3 и вовсе размер матрицы будет приближаться к количеству атомов во Вселенной (шутка).

2. Кроме того, разложение в ряд Тейлора точно только в окрестности данной точки, а при серьезном уходе от нее члены более высокого порядка могут давать существенный вклад. А гарантий, что достаточно мало - нет.

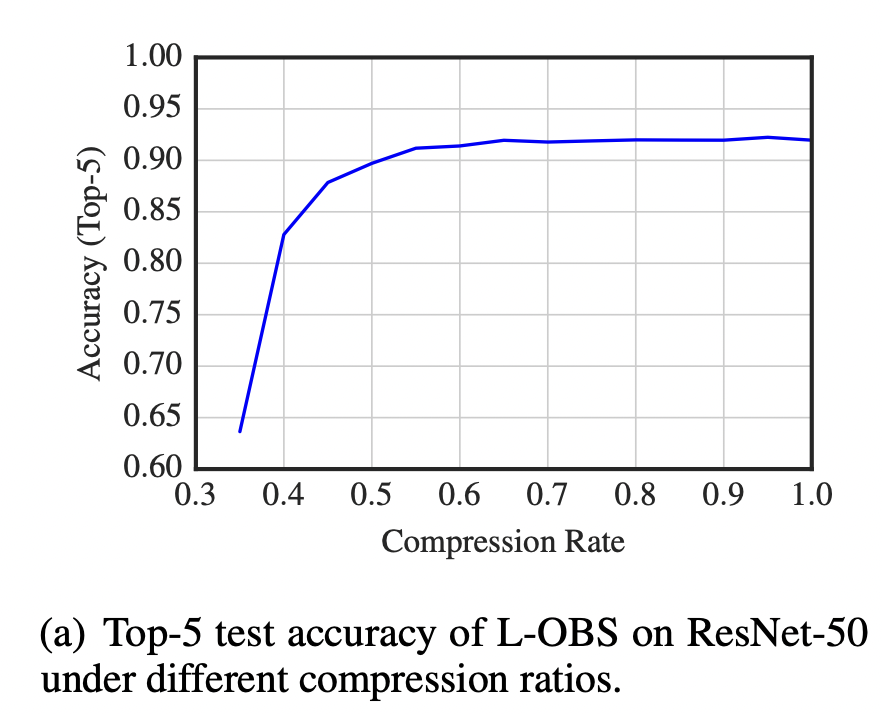
   Для обхода первой проблемы в работе было предложено считать матрицу Гессе только в пределах данного слоя. Такой подход дал лучшее качество по сравнению с magnitude-based бейзлайном.

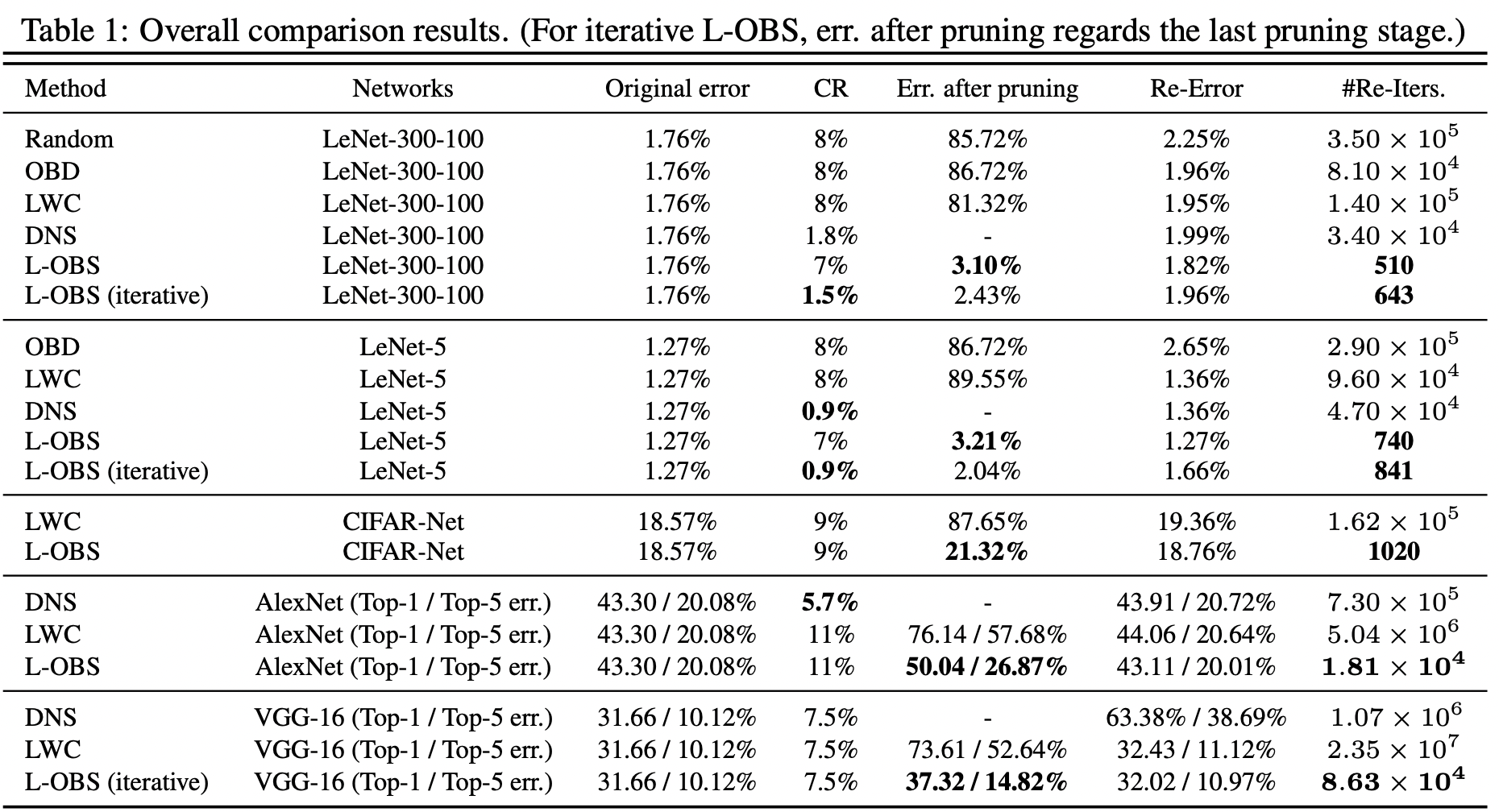
• Методы, основанные на - регуляризации

  • - регуляризация (и ее приближения)

    Естественной идеей кажется добавить в функцию потерь регуляризационный член следующего вида -

Но проблема в том, что такая фунция не дифференцируема в окрестности поэтому оптимизировать такую штуку градиентными методами не получится, а не градиентные методы сходятся не так резво и вообще неградиентная оптимизация вполне себе вызов.

Отсюда возникает мысль о том, чтобы заменить ступеньку в на что-то близкое, но гладкое, и первое, что приходит в голову - функция типа сигмоиды:

Параметр -  регулирует крутизну - чем больше тем ближе функция к ступеньке, и тем сложнее ее оптимизировать.

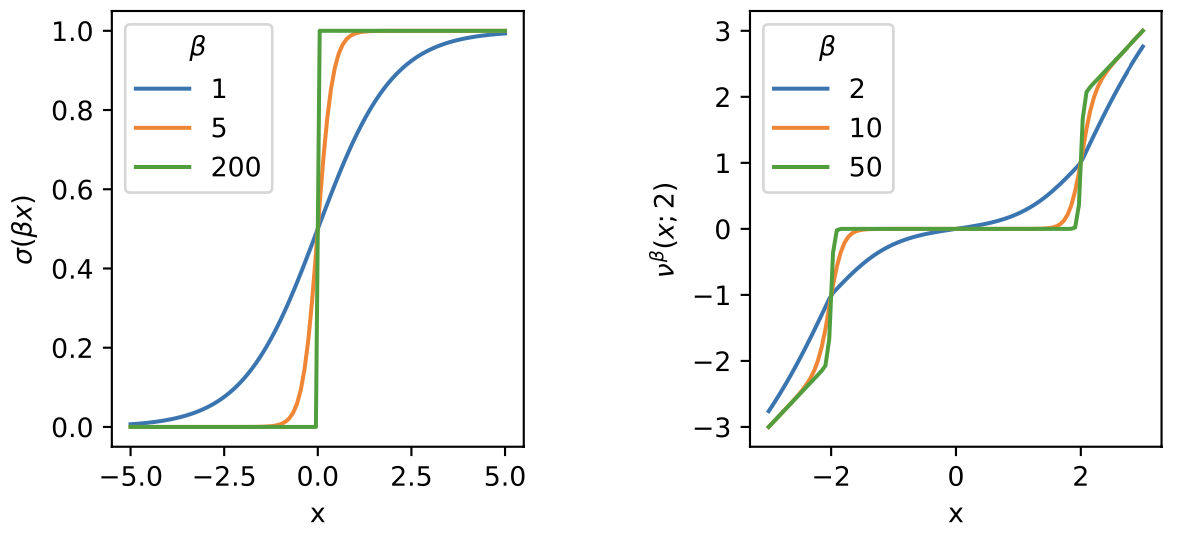
Добавление такого члена в фунцию потерь загоняет часть весов в значения, близкие к 0, и затем их можно отсеять, как в magnitude-based прунинге.

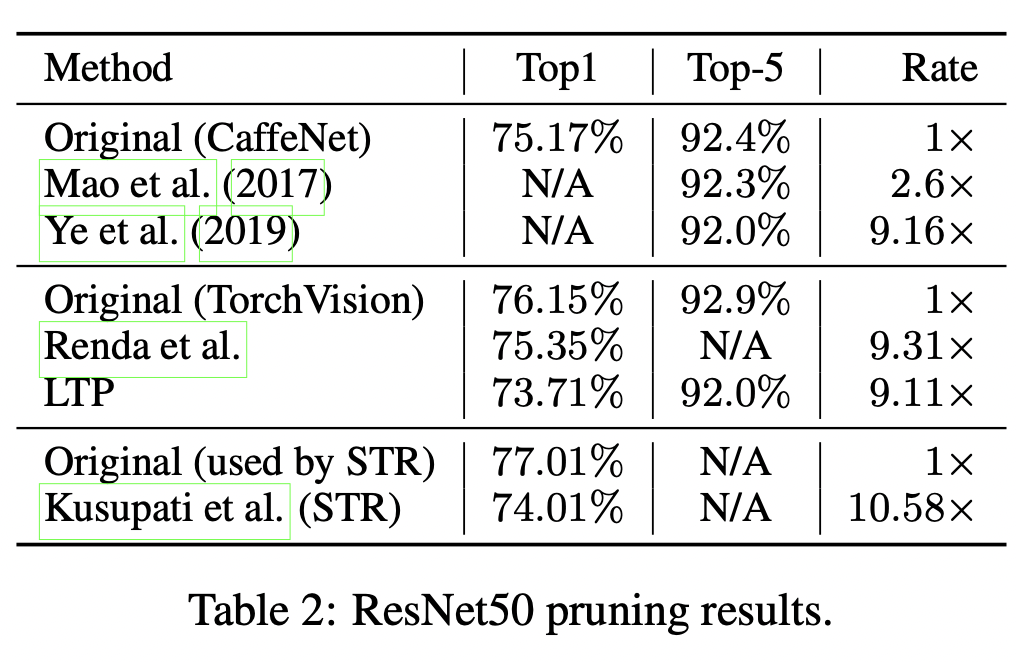
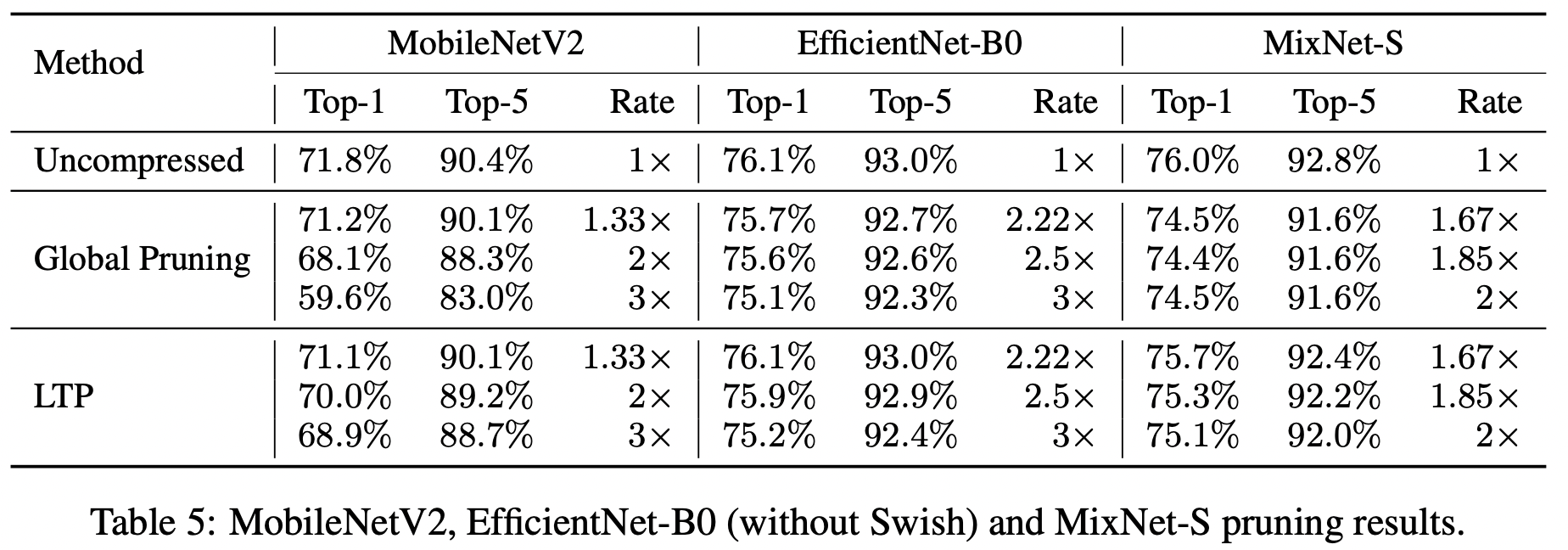
В работе данный подход был применен довольно успешно к ResNet50 и еще ряду современных сверточных архитектур.

• - регуляризация

  -регуляризация (она же Лассо) довольно хорошо себя зарекомендовала в задачах линейной регресии. При добавлении члена вида  в функцию потерь часть весов, в зависимости от коэффициента регуляризации, обращается тождественно в 0. Тем самым осуществляется feature selection. Увы, для глубоких сетей такого замечательное свойство не имеет места, а наличие регуляризации лишь ограничивает выразительную способность сети. Таким образом, утверждается, что такой метод оказывается не слишком полезным на практике.

• Методы, основанные на Байесовских подходах

  Если воспринять идею про то, что избыточные веса являются шумом в модели,  более близко к сердцу то вполне естественно перейти к Байесовской интерпретации задачи глубокого обучения. А именно, теперь значения весов мы считаем не фиксированными, а накладываем на каждый вес некоторое распределение вероятности.

  В оригинальной работе было предложено наложить на веса сети нормальное распределение , т.е с средним  и дисперсией

  Данный подход мотивирован работой по Гауссовому дропауту (Gaussian dropout), добавляющему мультипликативный шум , где было показано, что такой подход эквивалентен обычному дропауту, где накладывается

  бинарная маска на выходы, при условии

  То есть веса с большим значением - отвечают зашумленным весам, чье значение может существенно изменяться, без существенного изменения качества предсказания. Поэтому эти веса становятся кандидатами "на выход".

  Параметры являются обучаемыми точно так же, как и матожидания весов нейронной сети

  В функцию потерь добавляется дополнительный член - KL-дивергенция между априорным распредлелением на веса и апостериорным вместо которой затем считается Variational lower bound.

  В приведенных экспрериментах вариационный дропаут превосходит в плане эффективности другие современные ему подходы.

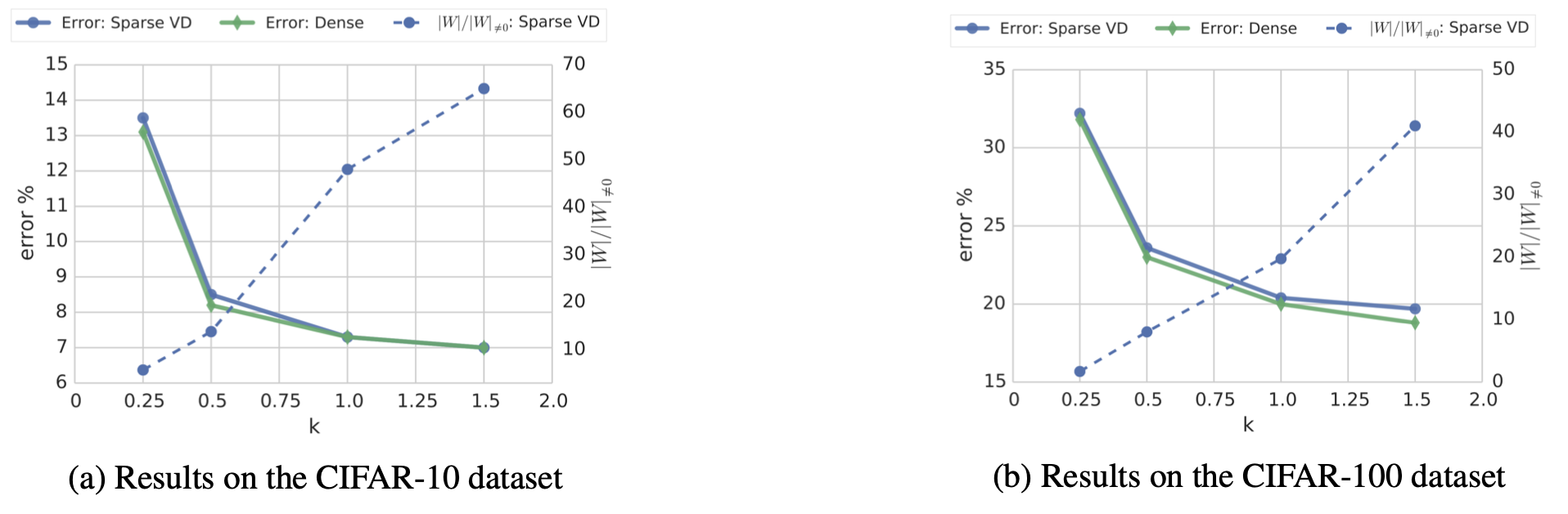
Методы обучения разреженной сети с самого начала

Рассмотренные выше подходы стартуют с плотной модели, где присутствуют все веса.Но вполне допустимо начать обучение с разреженной модели, занулив большую часть весов на первом шаге. Есть две основные стратегии дальнейшей оптимизации :

1. Фиксированная разреженность

   Маски нулевых и ненулевых весов зафиксированы на первом шаге, и не меняются в дальнейшем. (SNIP, GraSP)

2. Динамическая разреженность

   Время от времени маски весов обновляются - часть весов, что были отличны от нуля, прореживаются, но на их место добавляются новые веса, те, что ранее были нулевыми, согласно некоторому критерию (SET, RigL).

• SNIP (Single-shot Network Pruning based on Connection Sensitivity)

  SNIP определяет важные веса до начала обучения в зависимости от их влияния

  на лосс-функцию .

  Лосс-функция считается на одном батче, причем размер батча берется равным числу классов а задаче классификации.

  Лично мне кажется данный критерий довольно сомнительным , так как градиент в момент инициализации, а тем более на одном батче, не обязан быть сонаправлен с дальнейшей эволюцией весов.

  Кроме того, в случае большой степени разреженности может быть так, что в каком-то слое не останется живых весов вообще.А при наличии нулевой операции дальнейшей обучение сети невозможно.

  Но тем не менее, несмотря на вышеперечисленные соображения, в экспериментах такой способ работает довольно неплохо.

• SET и RigL

  SET и RigL, в отличие от  SNIP и GraSP, периодически обновляют маски весов. В качестве критерия отбрасывания используется старый добрый magnitude pruning. SET выбирает новые веса для наращивания случайным образом, RigL считает градиент в данной точке, сняв маску, чтобы градиент мог быть отличным от нуля для всех весов, и добавляет те веса - для которых градиент наибольший. То есть выбирает те веса, которые могут потенциально максимально изменить лосс-функцию.

  В работе по SET было показано, что обновление весов приводит к лучшему качеству, чем фиксированная разреженность. RigL, использующий более "умный" критерий наращивания весов, превосходит SET в приведенных экспериментах.

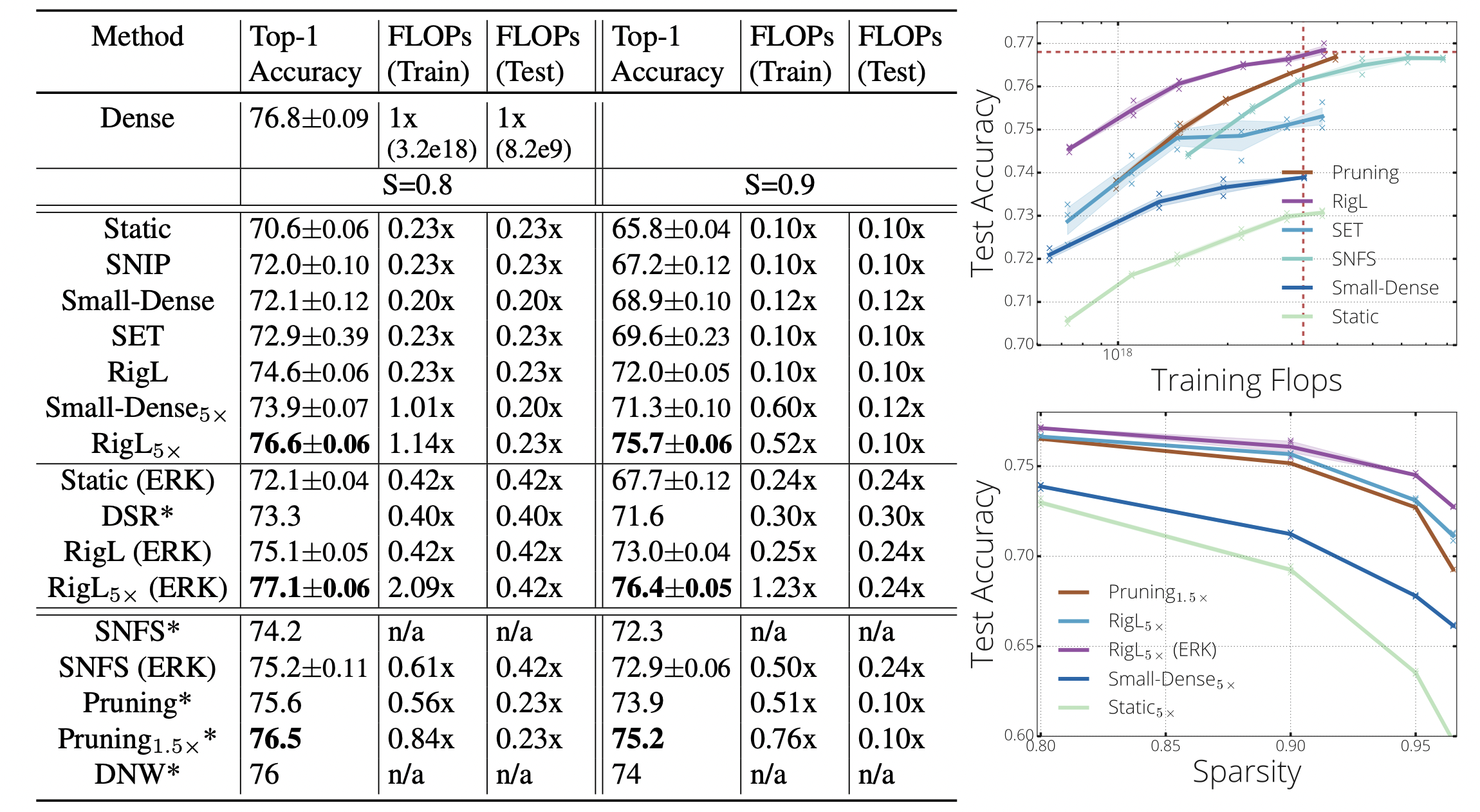
• GraSP (Gradient Signal Preservation)

  В этой работе было предложено использовать более сложный критерий, чем SNIP, для определения важности весов, использующий информацию второго порядка о функции потерь:

  Здесь - сдвиг, зануляющий данный вес.

  Наличие матрицы Гессе может подвергнуть сомнению применение данного метода на сетях, существенно отличных от игрушечных, но на самом деле данная матрица не вычисляется явно, а только произведение матрицы и вектора. (такая операция есть из коробки в Торче.

  Согласно приведенным в статье экспериментам, GraSP превосходит SNIP при прунинге ResNet32 на CIFAR-10(100). В то же время в большинстве случаев SNIP отрабатывает лучше на старушке VGG19.

Авторы утверждают, что при их подходе градиент имеет большую величину по сравнению с другими подходами, благодаря чему должна иметь место более быстрая сходимость процедуры обучения.

Ложка дегтя

Несмотря на активной деятельность в данной области и большое разнообразие идей и подходов, все же их применимость на практике достаточно ограничена. Основные критерии, по которым сравниваются разные методы -  Compression ratio (уменьшение количества параметров) и Theoretical Speedup (уменьшение числа операций сложения и умножения) - не всегда приводят к Practical speedup. Если для структуриванного прунинга выигрыша добиться гораздо проще, так как в итоге будет получен тензор с меньшим числом каналов или размером свертки, чем исходной, то для неструктурированного прунинга польза на практике наблюдается только при прореживании большого числа весов, так что можно перейти к представлению, работающему с разреженными тензорами.

Кроме того, как подмечено здесь, преимущество того или иного подхода сложно констатировать в силу следующих причин:

• Авторы статей не всегда приводят детали экспериментов, и зачастую при сравнении подходов используются разные настройки алгоритмов оптимизации, целевые функции. То есть, невозможно установить превосходство достингнуто за счет того, что данный метод лучше, чем другой, или процедура обучения оказалось удачнее.

• Алгоритм прунинга протестирован на небольшом числа датасетов и архитектур.

• Слишком мало точек на кривой Парето для того, чтобы делать какие-либо заключения.

• Нет доверительных интервалов и оценки погрешности. Отсюда велик риск, что результат может быть зависим от случайных факторов.

Продвинутый метод, использующий информацию второго порядка по лосс-функции, может в итоге не сильно переиграть в итоге простой и грубый magnitude-based прунинг.

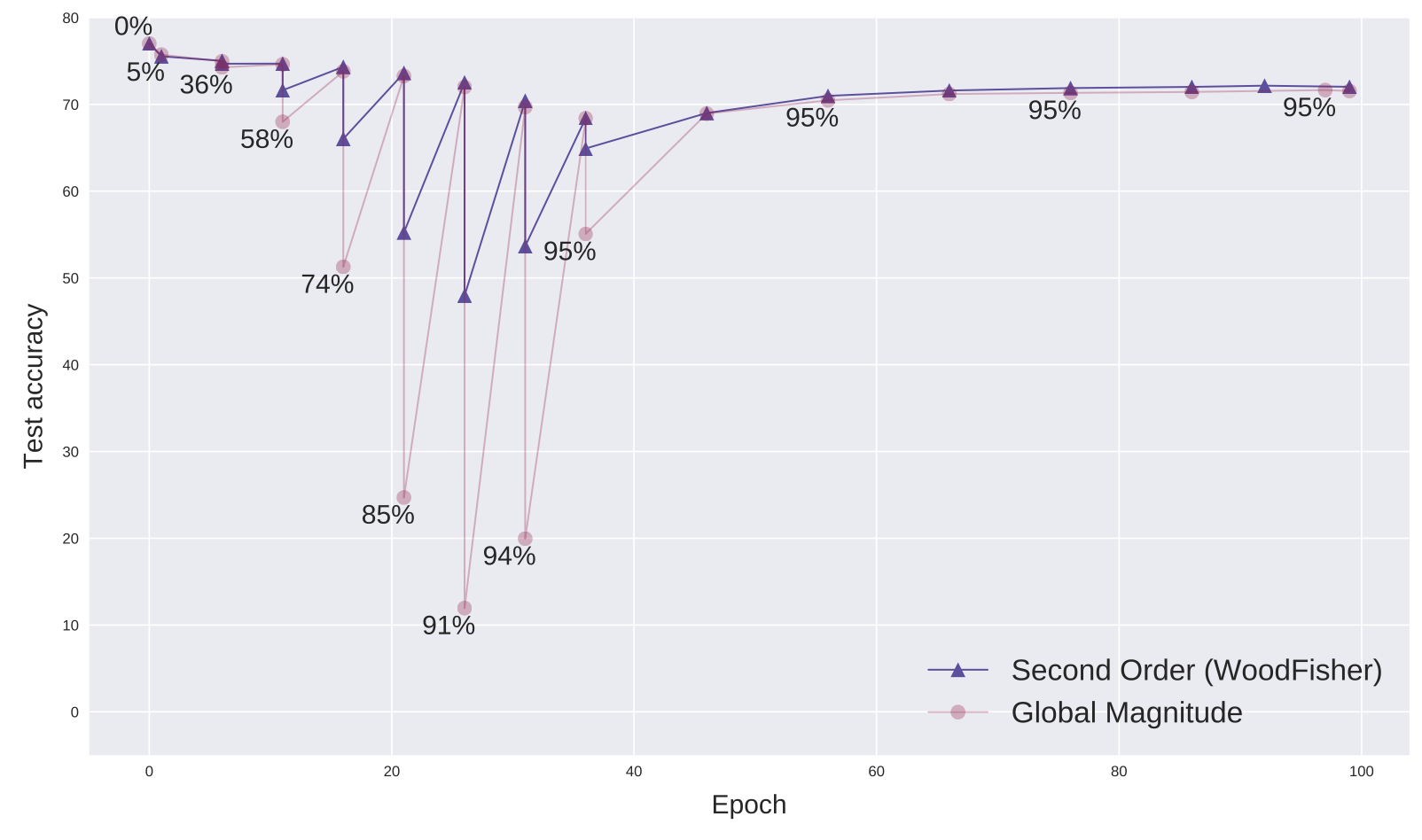
Кроме того, прореженная нейронная сеть может превзойти исходную архитектуру в плане эффективности, но, как часто бывает, пояляется новая архитектура, более совершенная и навороченная, и сколь ни хороша стратегия прореживания сети, выигрыш от прореживания не столь велик, как от перехода на новую архитектуру. Поэтому поиск архитектурных решений в целом считается более успешным и перспективным направлением.

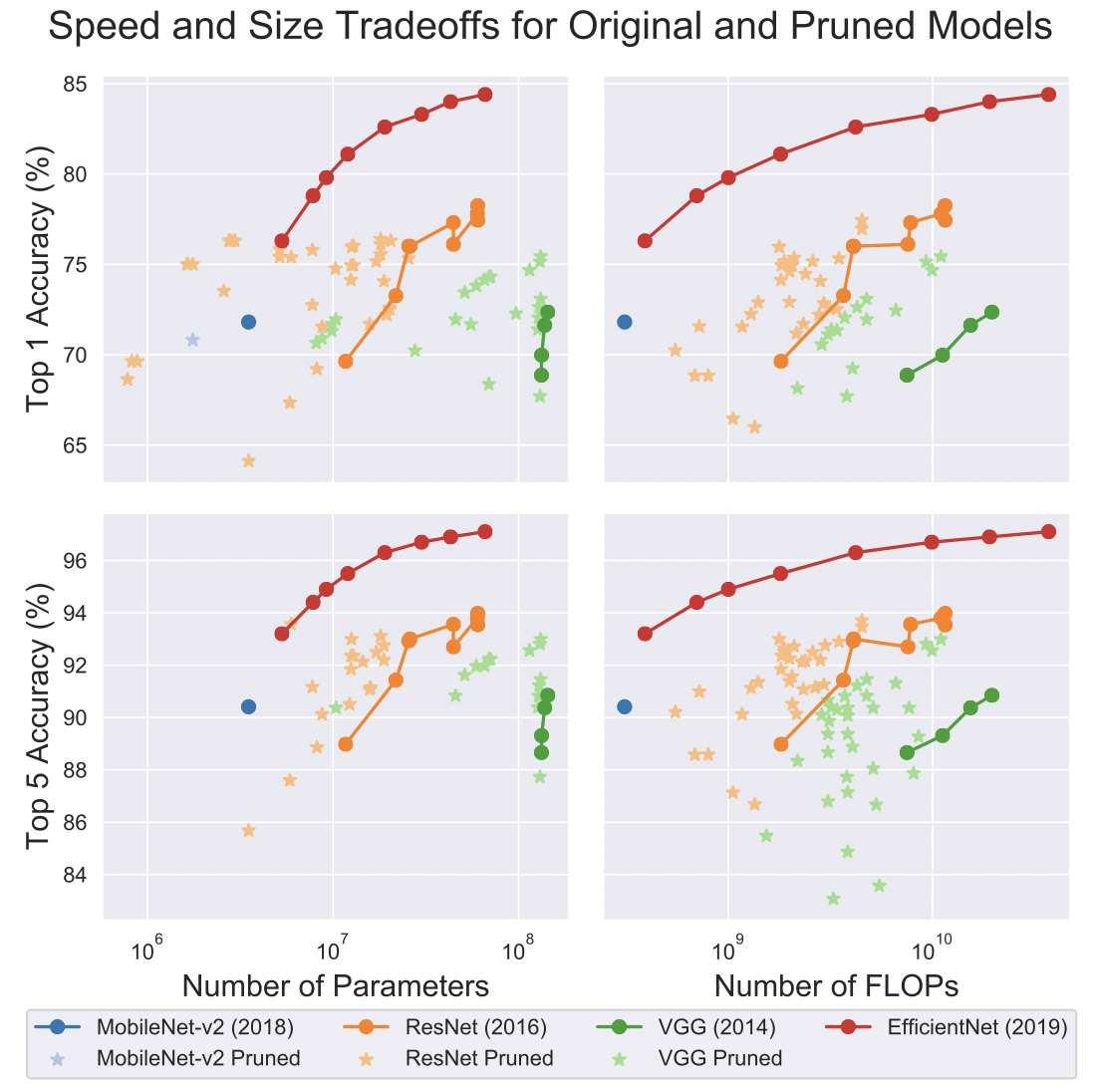
Различные методы прунинга на ImageNet

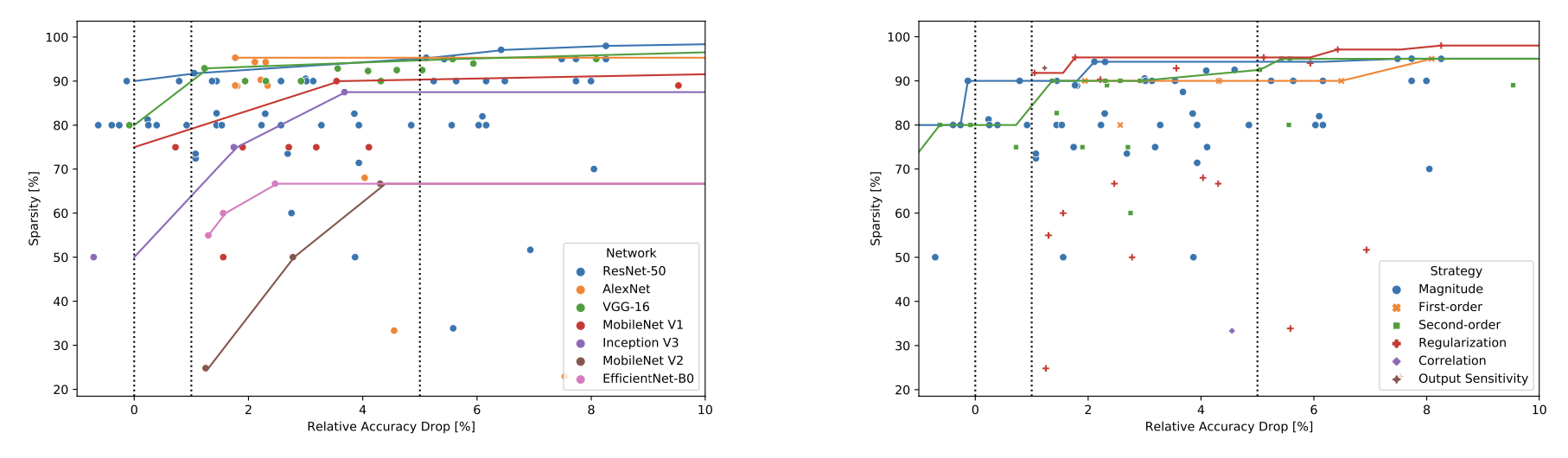
По всей видимости, различные методы прунинга дают более-менее сопоставимый результат в данной задаче. Можно заметить, что прунинг работает более эффективно на более старых архитектурах - AlexNet, VGG, ResNet, и не так хорошо на более современных MobileNet и EfficientNet. Это ожидаемый результат, так как последние две сети были спроектированы специально, чтобы более экономно и эффективно использовать параметры, нет той избыточности, от которой можно легко и безнаказанно избавиться.

Количество работ по различным методам прунинга

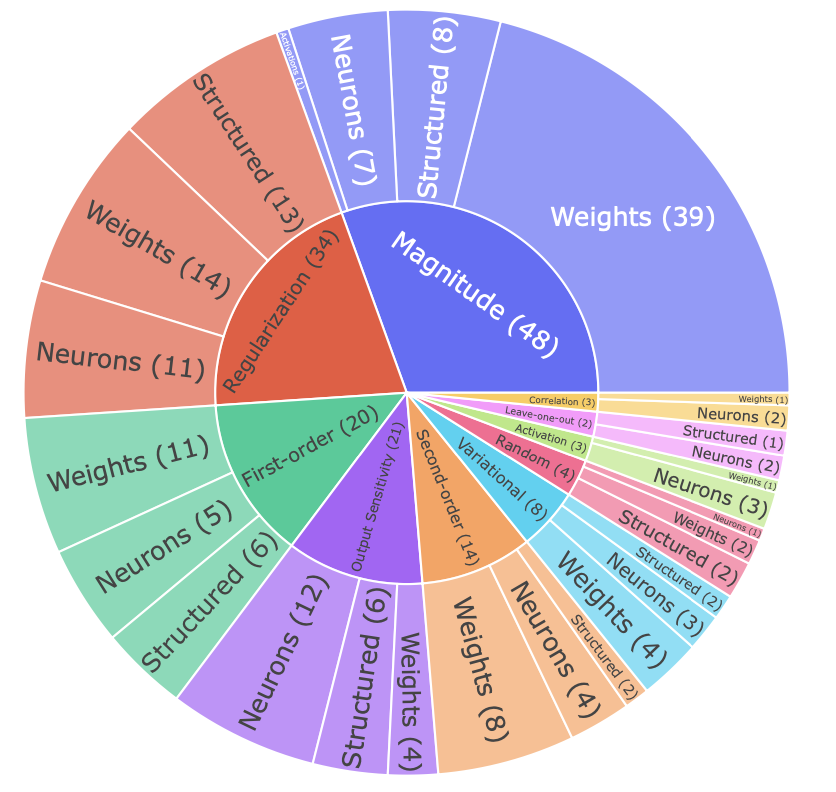
Заключение

Таким образом, прореживание нейронных сетей - это очень актуальная и интересная область деятельности, но в настоящий момент применимость прунинга на практике довольно ограничена. На текущий момент, не сколь либо строгой теории, гарантирующей успех или не успех той или иной стратегии прореживания. Тем не менее, потенциальный выигрыш и польза от сжатия сетей слишком заманчивы и мотивируют дальнейшиме исследования в этой области. Нет причин сомневаться в том, что в ближайшие несколько лет нас ждет кипучая деятельность в этом направлении и с ней множество интересных и вдохновляющих идей.

Список литературы

• Обзорные статьи

  Обширный обзор по прунингу, на основе которого во многом написана эта статья

  Обзор с сравнением различных подходов на бенчмарках (много графиков)

• Статьи по конкретным методам

  Optimal Brain Damage

  Optimal Brain Surgeon

  Layerwise OBS

  Magnitude-base pruning (первая работа)

  Magnitude-based pruning (работа  Han et al.)

  Learned Threshold Pruning

  Variational Dropout

  SNIP

  SET

  RigL

  GraSP

• Туториалы по принингу

  Tensorflow

  PyTorch